賦值法求系數和

福建 蔡愛兵

賦值法求系數和

福建 蔡愛兵

二項式定理為高考的必考考點，常見題型為選擇題、填空題，以計算某一項的系數或者某幾項系數之和為主，主要是考查二項式定理和賦值法，一般是基礎題或者中檔題，在備考復習時，要側重基礎.本文結合最近幾年高考試題中考查二項式定理的部分，主要探討賦值法求系數和.

一、針對特定一項的1賦值法

( )

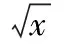
A.-1 B.0

C.1 D. 2

【評注】考查對二項式定理和二項展開式的性質，重點考查實踐意識和創新能力，體現正難則反.

【例2】(2012·浙江理·第14題)若將函數f(x)=x5表示為f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5，其中a0,a1,a2，…,a5為實數，則a3=________.

【解析】法一：應用二項展開式，等式兩邊對應項系數相等.

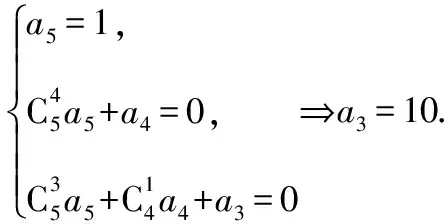
法二：對等式f(x)=x5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5兩邊連續對x求導三次得60x2=6a3+24a4(1+x)+60a5(1+x)2，再運用賦值法，令x=-1得60=6a3，即a3=10.

【評注】求某項系數，先求導數，把要求的項系數變為常數項，在賦值，只留下常數項，事半功倍.

二、針對奇偶項的-1，1賦值法

【例3】(2015·全國新課標Ⅱ理·第15題)(a+x)(1+x)4的展開式中x的奇數次冪項的系數之和為32，則a=________.

【解析】法一：應用二項展開式，(1+x)4=1+4x+6x2+4x3+x4，故(a+x)(1+x)4的展開式中x的奇數次冪項分別為4ax,4ax3,x,6x3,x5，其系數之和為4a+4a+1+6+1=32，解得a=3.

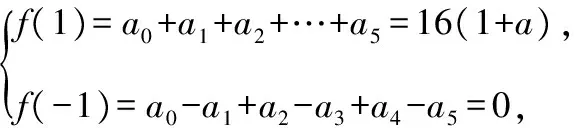
【評注】本題考查二項式定理，準確寫出二項展開式，能正確求出奇數次冪項以及相應的系數和，從而列方程求參數值，屬于中檔題.

( )

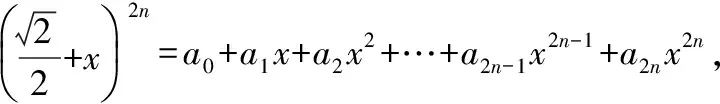
A.-1 B.0

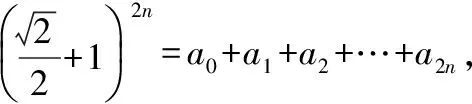
【評注】本題主要是考查二項式定理奇偶項系數，直接計算比較繁瑣，先變形再賦值，則相對簡單.

三、針對所有項的1賦值法

( )

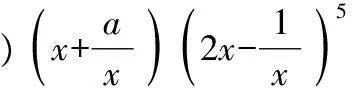
A.-40 B.-20

C.20 D.40

【評注】本題關鍵在于各項系數之和的賦值計算，求出a，再應用二項式展開式，計算常數項.

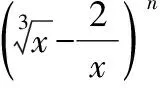
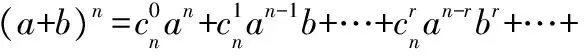
福建省漳州市臺商投資區廈門雙十中學漳州校區)