基于灰狼群智能最優化的神經網絡PM2.5濃度預測

石 峰,樓文高,2,張 博

(1.上海理工大學 光電信息與計算機工程學院,上海 200093; 2.上海商學院 信息與計算機學院,上海 200235;3.上海理工大學 出版印刷與藝術設計學院,上海 200093) (*通信作者電子郵箱79379816@qq.com)

基于灰狼群智能最優化的神經網絡PM2.5濃度預測

石 峰1,樓文高1,2,張 博3*

(1.上海理工大學 光電信息與計算機工程學院,上海 200093; 2.上海商學院 信息與計算機學院,上海 200235;3.上海理工大學 出版印刷與藝術設計學院,上海 200093) (*通信作者電子郵箱79379816@qq.com)

針對目前PM2.5濃度測量成本高和測量過程繁雜等問題，建立了基于灰狼群智能最優化算法的神經網絡預測模型。從非機理模型的角度，結合氣象因素和空氣污染物對上海市的PM2.5濃度進行預測，并使用平均影響值分析了影響PM2.5濃度的重要因素。使用灰狼群智能算法優化神經網絡的過程中，引入了檢驗樣本實時監控訓練過程以避免發生“過訓練”現象，確保建立的神經網絡模型具有較好的泛化能力。實驗結果表明：PM10對PM2.5的影響最為顯著，其次是CO和前一天PM2.5。選取2016年11月1日—12日的數據進行驗證，其平均相對誤差為13.46%，平均絕對誤差為8 μg/m3，與粒子群算法優化的神經網絡、BP神經網絡模型及支持向量回歸(SVR)模型的誤差相比，平均相對誤差分別下降了約3個百分點、5個百分點和1個百分點。因此，使用灰狼算法優化的神經網絡更適合上海市PM2.5濃度的預測和空氣質量的預報。

灰狼優化算法;BP神經網絡;PM2.5濃度預測;預測模型;空氣污染物

0 引言

空氣污染問題變得越來越嚴重,不僅對汽車行業、建筑業、環保行業等社會支柱產業發展產生很大影響,對商貿服務業等第三產業發展、產業結構轉型和高層次人才引進等也會造成重大影響[1],同時對城市居民的身體健康也構成很大威脅[2]。我國沿海大城市大氣污染的主要來源是機動車尾氣、中長途傳輸的沙塵、生活物質燃燒、城市揚塵等[3-4],除此之外,污染物與氣象要素之間的交互作用[5-7]對大氣污染的影響也很顯著。在大氣污染物中，PM2.5是關注的重點對象,其測量成本高、測量過程繁雜等因素給空氣質量發布帶來不便,為此從非機理角度,建立可靠、合理的PM2.5濃度預報模型,對PM2.5監測和發布空氣質量指數具有重要的理論意義和實踐價值,是環保部門和環境科學與工程學界的熱點和難點問題。

空氣質量的影響因素較為復雜,國內外對空氣質量研究的模型主要有機理模型和非機理模型。機理模型的預報模式主要以數值預報為主,數值預報的準確率主要受到模式分辨率、污染源排放資料和空氣質量監測數據等諸多因素影響[8]。目前數值預報采用的主要模型多尺度空氣質量(Community Multiscale Air Quality, CMAQ)模型[9]、天氣預報模式(Weather Research and Forecasting Model, WRF)與CMAQ結合的WRF-CMAQ模型、[10]、WRF-Chem模型[11]、多模式集合預報[12]等,王占山等[13]對CMAQ模型在大氣污染物各方面的應用研究作了總結,并指出了國內外使用該模型研究的主要方面有評價模型的模擬性能，模擬預測空氣中污染物濃度以及研究各污染物的來源、產生機理及傳輸擴散過程。使用機理模型對空氣質量進行預報,預報的精度相對比較高,但需要考慮復雜的物理化學過程、氣象、污染物擴散、邊界層條件等綜合因素,進而造成預報系統計算復雜、軟硬件要求高。而非機理模型是通過歷史數據獲取數據特征、發現潛在的變化規律,簡化了空氣質量預報的影響因素,方便在實際中應用,近年來在實際應用中已經逐漸成熟。當前國內外采用的非機理模型主要有基于自回歸移動平均模型(Autoregressive Integrated Moving Average Model, ARIMA)[14-15]、多元線性回歸模型(Multivariable Linear Regression Model, MLR)[16-17]、灰色理論預測模型[18-19]、支持向量機(Support Vector Machine, SVM)[20-21]、神經網絡模型(Artificial Neural Network, ANN)[22-28]的大氣污染物濃度預測。經分析可發現：ARIMA模型、灰色模型和多元線性(實際上是冪函數)等確定型模型雖然在預測PM2.5濃度中具有一定的適用性,但是沒有考慮到污染物之間的相互作用等,而神經網絡恰能夠模擬這種機理不明確的非線性系統。文獻[22]采用概率神經網絡(Probabilistic Neural Network,PNN)模型只能進行分類(定性)研究,而文獻[23-28]雖然采用T-S、小波及粒子群算法等優化算法改進BP神經網絡模型性能和收斂速度,取得了一定效果,但本質上仍然是采用反向傳播(Back Propagation, BP)神經網絡建模,而BP神經網絡建模的最大問題是訓練時很容易出現“過訓練”現象,從而導致建立的模型沒有泛化能力和實用價值。這些文獻中大多沒有遵循BP神經網絡建模的基本原則和步驟[32,38],泛化能力和預測能力值得進一步的探討和研究。

從非機理模型的角度出發,針對當前使用神經網絡在空氣質量預報應用中存在的問題,本文在進行建模時遵循神經網絡建模基本原則和步驟,建立了基于灰狼優化的神經網絡模型對上海市PM2.5日均濃度進行預測,分析了灰狼優化的神經網絡模型的泛化能力、有效性和魯棒性。研究結果表明:群智能灰狼最優化算法克服了BP算法收斂速度慢和易陷入局部最優等缺陷,收斂性能好,通過采用檢驗樣本實時監控訓練過程以避免發生“過訓練”現象,確保建立的模型具有較好的泛化能力,根據建立模型的測試樣本、預測樣本與訓練樣本和檢驗樣本具有相似的精度,說明建立的PM2.5濃度預測模型具有較好的預測能力和實用價值,可以為PM2.5濃度監測和發布空氣質量指數提供可靠的依據和預測模型(方法)。

1 模型原理

1.1 BP神經網絡

BP神經網絡是一種多層前饋神經網絡,網絡結構包含輸入層、隱含層和輸出層,通過樣本的訓練尋求合適的網絡權值和閾值。關于BP神經網絡的詳細原理請參考文獻[29-30]。BP神經網絡有諸多的優點,但由于網絡結構過大以及過度訓練都會造成訓練過程出現“過訓練”現象而陷于局部最優,收斂性能差。因此,應用BP神經網絡建模必須遵循一定的建模原則和基本步驟[31-33,38]。

1.2 灰狼優化神經網絡的算法

Mirjalili等[34]在2014年提出了灰狼優化(Grey Wolf Optimizer, GWO)算法,是一種新型群智能優化算法,通過模擬自然界中灰狼尋找、包圍和攻擊獵物等狩獵機制的過程來完成最優化工作。該算法將狼群劃分為4個等級,將狼按照適應度值最優排序,選擇適應度值的前3個分別作為最優灰狼α,次優灰狼β和第三優灰狼δ,剩余灰狼作為ω。在捕食過程中,由α、β、δ灰狼進行獵物的追捕,而剩余灰狼ω追隨前三者進行追蹤和圍捕,獵物的位置便是問題的解。研究證明GWO算法在全局尋優方面明顯優于粒子群優化(Particle Swarm Optimization, PSO)算法、遺傳算法(Genetic Algorithm,GA)和進化策略(Evolutionary Strategy, ES)等智能優化算法[34-35]。因此,本文利用GWO來優化BP神經網絡的權重和閾值。下面給出灰狼算法的主要數學模型:

定義1 定義獵物所在位置的全局最優解及個體與獵物間的距離向量D。

D=|C·Xp(t)-X(t)|

(1)

C=2r1

(2)

其中:Xp(t)表示第t代獵物的位置;X(t)表示第t代灰狼個體當前的位置;C表示向量系數;r1為[0,1]內的隨機數。

定義2 灰狼向獵物移動過程中,個體的更新方式。

(3)

A=2ar2-a

(4)

其中:A為收斂因子;r2表示為[0,1]內的隨機數;a表示在迭代過程中隨著迭代次數增加從2遞減至0;Xω(t+1)表示灰狼個體更新后的位置。

灰狼優化算法是一種能夠尋找全局最優解的群智能算法,具有加速模型收斂速度快和提升精度等特點,將BP神經網絡的權重和閾值作為灰狼的位置信息,根據灰狼對獵物的位置判斷,不斷更新位置,就等同于在不斷更新權重和閾值,最終尋得全局最優。具體優化神經網絡過程如下:

Step1 確定神經網絡結構,主要是隱層節點的選取。

Step2 初始化參數。根據網絡結構計算灰狼個體位置信息的維度(dim)、灰狼種群大小(SN)、最大迭代次數(maxIter)、灰狼維度的上界(ub)和下界(lb),隨機初始化灰狼位置。

Step3 確定神經網絡適應度函數及隱層節點、輸出節點的激勵函數,其中適應度函數選用均方誤差(Mean Squared Error,MSE),隱含層和輸出層的激勵函數均采用Sigmoid型函數。

Step4 計算適應度值,選取最優灰狼α、次優灰狼β和第三優灰狼δ,根據式(3)更新剩余灰狼ω的位置信息，并更新參數A和C及a。

Step5 記錄訓練樣本和檢驗樣本的誤差及所對應的最優灰狼α的位置。

Step6 判斷個體每一維度是否存在越界,將越界的值設置為灰狼維度的上界(ub)或下界(lb)。

Step7 判斷是否滿足設定的誤差或者達到最大迭代次數;否則重復Step4～Step7,直到滿足條件。

Step8 最后返回結果為最優灰狼位置α及對應的最小誤差；訓練樣本和檢驗樣本的誤差及訓練過程每一次迭代最優灰狼α的位置。

2 建立PM2.5濃度預測模型

本文空氣質量數據來源于上海市空氣質量實時查詢系統(http://www.semc.gov.cn/aqi/home/Index.aspx),氣象數據來源于天氣網 (http://lishi.tianqi.com/shanghai/index.html)。選取上海市2013年1月1日(之前沒有公布這方面的數據)至2016年10月31日空氣污染物數據及氣象數據(1 400組)為原始數據,對上海市PM2.5濃度建立預測模型。從獲取的原始數據可以看出,初步選取的指標包括氣象因素(天氣狀況、溫度、風向和風速)和空氣污染物(PM10、NO2、SO2、CO、O3)。

2.1 選取影響PM2.5濃度的因素

根據上海的氣溫季節性變化明顯,習慣將上海的四季劃分為12月—次年的2月為冬季、3月—5月為春季、6月—8月為夏季、9月—11月為秋季。分別統計上海春夏秋冬四季的PM2.5濃度值為75 μg/m3、55 μg/m3、59 μg/m3、102 μg/m3,可以看出上海市的PM2.5季節變化特征是冬季gt;春季gt;秋季gt;夏季,表明上海市的PM2.5濃度具有季節性變化特征,這與湯羹等[6]研究的結果一致。

原始數據中,天氣狀況有15種類型,將其劃分為晴天、多云、陰天、雨天和雪天,分別統計這些天氣所對應的PM2.5濃度,其中晴天的平均濃度最高為91 μg/m3,多云和陰霧天氣的平均濃度為77 μg/m3和71 μg/m3,晴天平均濃度最高；進一步的統計分析,發現污染天氣的占比是33%(晴天數為300天),空氣優良的占66%；進一步的分析發現在99天的污染空氣中,春夏秋冬四季的占比分別是 31.33%、0%、15.15%、53.52%。由此可見：晴天的濃度最高是因為高濃度天氣發生在春冬季節,使最終的平均濃度值偏大；雨天和雪天的PM2.5的平均濃度是56 μg/m3和48 μg/m3偏低,在雨和雪的作用下能夠稀釋PM2.5污染物的濃度。

圖1繪制了2013年01月01日—2016年10月31日內月份PM2.5均濃度和均溫度曲線。從圖1中可以看出,溫度與PM2.5濃度的影響比較明顯,隨著溫度的升高PM2.5濃度在逐漸的降低,在8月份和9月份達到最低為45μg/m3,而溫度的降低會導致PM2.5的濃度升高,在12月份和1月份均值較高都超過了75 μg/m3。溫度明顯的特征變化,使得上海的四季分明。PM2.5濃度隨溫度變化的原因是:隨著溫度逐漸升高,混合層高度越大,污染物越容易在垂直方向上稀釋; 反之,污染物容易聚集在近地層,導致污染物濃度上升[36];溫度比較低,容易產生逆溫現象,空氣污染物容易沉集致使空氣污染物濃度升高[7,36]。

圖1 PM2.5月均濃度與月份和溫度的關系

風向與風速為2個因素,上海的地面風為偏西風時,會伴隨著高污染物濃度出現,且冬季盛行偏西風,夏季多東南風,來自海上的清潔空氣對空氣污染物濃度具有一定稀釋作用,大量的降雨對去除污染物濃度也具有顯著作用[6]。綜合文獻[22-28]所選取的氣象因素和污染物因素,本文最后選取天氣狀況、溫度和風速作為氣象因素，選取PM10、NO2、SO2、CO、O3這5種作為空氣污染物。

2.2 數據預處理和樣本分組

由于指標間的數據的量綱不同,為減小對模型造成的不利影響,要對數據進行歸一化處理。進行量化處理時,要考慮到指標對實際PM2.5濃度的影響,而且不同的量化方式對結果產生的影響不同,依據2.1節分析,作出如下量化處理:1)天氣狀況(X1),對雨天、晴云、多云、陰霧和雪天分別量化為1、2、3、4和5來表示；2)溫度(X2)，溫度按照四季的PM2.5濃度均值比值來量化;3)上海來自偏東方向的風有助于污染物濃度的擴散,而偏西方向會加重污染物濃度,因此將風速分解為東西方向(X3)和南北方向(X4)來表示。對量化后的數據采用最大最小歸一化處理,其計算公式為:

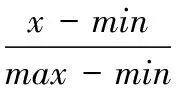
(5)

其中:x(*)表示歸一化后的數據;x表示原始數據;min表示每一個指標的最小值;max表示每一個指標的最大值。將數據歸一化到0.2～0.8。通過以上的量化處理后最終的指標體系包括:天氣狀況(X1)、溫度(X2)、東西向風速(X3)、南北向風速(X4)、PM10(X5)、NO2(X6)、SO2(X7)、CO(X8)、O3(X9)、前一天PM2.5(X10)濃度共10個指標。針對這1 400組數據歸一化后,使用自組織映射(Self Organizing Mapping, SOM)算法將樣本按照3∶1∶1的比例[32]劃分為訓練樣本、檢驗樣本和測試樣本,三類樣本的數量分別為:712、344和344。其中:訓練樣本用來訓練整個網絡模型;檢驗樣本用來監控在訓練過程中是否出現“過訓練”現象;測試樣本用來判斷所建立模型是否具有泛化能力。

2.3 確定合理的神經網絡結構

BP神經網絡在解決實際的問題時,主要考慮的是隱層數和隱層節點的個數與研究問題的復雜程度等。Hecht-Nielsen[37]證明了一個三層的BP神經網絡能夠完成m維向n維的任意映射,因此隱層數選擇一層。針對隱層節點個數的選取,樓文高等[32]指出目前確定隱層節點個數的各類公式都不具有一般性,可以作為初步參考值,通常采用試湊法[38]來確定。根據BP神經網絡建模基本原則,訓練樣本數量要多于網絡連接權重個數的3～5倍以上,達到5～10倍則更好[33]。因此,對于本例,隱層合理節點個數應在3～17范圍內。表1為采用不同隱層節點個數(N)時建模實驗所得到的訓練樣本、檢驗樣本和測試樣本(簡稱三類樣本)的均方根誤差,該數值是反歸一化后的結果。

從表1中可以看出隨著隱層節點個數的增加,訓練樣本誤差逐漸減小且最終誤差變化不大,而檢驗樣本和測試樣本的誤差隨隱層節點個數的增加,到9個節點時達到最小而后又有所增大,說明隱層節點個數不是越多越好,而是存在一個合理的隱層節點個數,隱層節點過多,容易發生“過擬合”現象。遵循選取合理隱層節點個數的原則,應當選取檢驗樣本最小時隱層節點個數, 綜合考慮,最終確定隱層節點的合理個數為9。

表1 不同隱層節點個數時的三類樣本均方根誤差對比

2.4 建立預測PM2.5濃度的模型

本文使用R軟件來進行建模,經多次實驗,GWO優化的神經網絡參數如下:狼群的數量為200;初始位置的上界和下界為3和-3;最大迭代次數為150;網絡結構為10-9-1,即輸入層有10個節點(變量個數),9個隱層節點和1個輸出節點(PM2.5濃度)。為確保模型具有泛化能力,要確保測試樣本誤差與訓練樣本誤差、檢驗樣本誤差相當或者小于它們的1.20倍[38]。遵循這一原則,隨機初始化神經網絡的權重和閾值進行100次以上反復的訓練,其訓練過程如圖2所示。

圖2 模型訓練過程誤差(歸一化數據)曲線

訓練樣本、檢驗樣本和測試樣本的均方根誤差分別為16.24 μg/m3、13.48 μg/m3和13.21 μg/m3;平均絕對誤差分別為11.29 μg/m3、10.12 μg/m3和9.79 μg/m3;平均相對誤差分別為17.14%、16.77%和15.41%;預測值與實際值的Pearson系數分別為0.939 8、0.959 2和0.954 8。

3 結果與討論

3.1 模型性能分析

將上海市2016年11月1日—12日(共12個樣本)氣象數據和空氣污染物數據用同樣方式歸一化后,使用GWO優化的神經網絡模型和PSO優化的神經網絡模型、支持向量回歸(Support Vector Regression, SVR)模型進行對比。為了使所建模型具有說服力,訓練過程使用相同的訓練樣本及歸一化方式。其中PSO優化的神經網絡模型參數設置為:網絡結構采用10-9-1,慣性權重w=0.729,加速因子c1=c2=1.496 28,粒子速度范圍[-0.6,0.6],粒子的邊界范圍[-3,3],最大迭代次數150,粒子的個數200。SVR模型借助LIBSVM工具箱建模,使用網格搜索算法和交叉驗證訓練參數,得出模型的參數為:懲罰因子c=5.278,核函數采用徑向基函數,核函數參數g=0.062 5,交叉驗證參數v=5,ε-不損失函數值p=0.01。為了能夠說明模型的適用性,前一天PM2.5濃度都采用預測值,其預測值和真實值的結果如圖3所示。

圖3 PM2.5濃度預測值與實際值的比較

對不同方法優化的神經網絡模型的性能參數如表2所示。

表2 不同模型的預測誤差比較

注：相關系數表示預測值與真實值的相關系數。

從表2可看出：GWO優化的神經網絡模型在PM2.5濃度預測方面要優于PSO優化的神經網絡模型、BP神經網絡模型及SVR模型,且GWO優化的神經網絡的預測誤差與訓練樣本、檢驗樣本和測試樣本誤差對比分析,檢驗樣本在實時監控訓練過程沒有發生“過訓練”現象,測試樣本誤差與訓練樣本誤差相當或小于它們的1.2倍,而預測樣本的誤差較小,說明模型具有很好的泛化能力、預測能力和適用性。所建立的GWO優化的神經網絡模型適合對PM2.5濃度預測。

3.2 不同污染等級誤差分析

根據《環境空氣質量指數(AQI)技術規定(試行)》(HJ633—2012)規定,空氣質量指數(ρ) 等級劃分的對應關系為:ρ≤50為優、50lt;ρ≤100為良、100lt;ρ≤150為輕度污染、150lt;ρ≤200為中度污染、200lt;ρ≤300為重度污染和為ρgt;300嚴重污染共6個等級,指數越大污染越嚴重,而且PM2.5分指數可以通過PM2.5濃度計算獲取。對上海市2013年1月1日—2016年10月31日PM2.5分指數進行統計結果為:0～50(518天)、50～100(607天)、100～150(184天)、150～200(56天)、200～300(33天)和300～500(2天),因此,可以看出上海PM2.5的污染這3年來多處于優良(80.36%)及輕度污染(13.14%),高度污染(6.5%)所占比例較小。利用所建立的GWO 優化神經模型對不同天氣污染等級計算誤差結果如表3所示。

表3 不同天氣污染等級誤差結果

從表3可以看出,不同天氣污染等級的平均絕對誤差最大不超過32 μg/m3(重度污染時),原因是重度污染天氣的濃度高且數據平穩性差,經常出現突增情形,所以預測的絕對誤差相對比較大;平均相對誤差最大(等級為優時)為20.85%,天氣為優時濃度較低且占據的天數比較多,也可能使得平均相對誤差偏大;而其他等級的平均相對誤差在11%左右,對天氣污染等級預報的正確率80.43%。因此,所建立的GWO優化的神經網絡模型在不同天氣污染等級預測方面具有較好的正確性和可靠性,適合對污染天氣作預報。

3.3 影響PM2.5的重要因素

Dombi等[39]提出了一種利用平均影響值(Mean Impact Value, MIV)來反映神經網絡各個輸入指標對目標指標的影響程度,是目前分析變量(指標)重要性的最好方法之一。使用MIV不僅可以有效分析輸入變量對輸出變量的重要性,還可以分析指標的性質(正向指標還是逆向指標),絕對值大小表示影響程度。據此可以分析影響PM2.5濃度各個因素的重要性及其排序,如表4所示。

表4 各個變量(指標)的MIV值

從表4中可以看出,在10個輸入變量中,天氣狀況(X1)、SO2(X7)和NO2(X6)呈現負相關,是逆向指標,而溫度(X2)、東西向風速(X3)、南北向風速(X4)、PM10(X5)、CO(X8)、O3(X9)、前一天PM2.5(X10)濃度呈現正相關,是正向指標;對PM2.5的影響程度從大到小依次排序為:X5gt;X8gt;X10gt;X9gt;X2gt;X7gt;X1gt;X3gt;X4gt;X6。在氣象因素中,溫度(X2)的影響最大,次之是天氣狀況(X1),風速的影響很小;在空氣污染物中,PM10(X5)的影響最大,其次是CO(X8),再次是前一天PM2.5(X10)和O3(X9)。在整個指標體系中,PM10的影響最顯著,其次是CO,它們的影響程度顯著大于其他所有指標。

4 結語

本文在遵循神經網絡建模基本原則和步驟的前提下，綜合考慮了氣象因素和大氣污染物對PM2.5濃度的影響，建立了GWO算法優化神經網絡的PM2.5濃度預測模型，使用檢驗樣本監控訓練過程以避免發生“過訓練”現象。從誤差分析結果來看，該模型在PM2.5濃度的預測方面要優于PSO優化的神經網絡模型、BP神經網絡模型及SVR模型。測試樣本和預測樣本具有與訓練樣本和檢驗樣本相似的誤差精度，說明本文建立的基于GWO的PM2.5濃度預測模型具有較好的泛化能力、預測能力和魯棒性,具有較好的實用價值。將該模型應用于不同天氣污染等級的預報上，結果表明該模型對不同天氣污染等級的預報,也具有良好的效果。文中使用MIV值研究影響PM2.5因素的重要性，結果表明:氣象因素中溫度影響最大，空氣污染物中PM10影響最為顯著。本文在建模過程中發現GWO算法雖能達到全局最優，但后期收斂速度較慢，同時考慮到其他氣象因素(濕度、壓強等)也會對PM2.5濃度產生影響，鑒于此在以后的研究中將進一步改進網絡模型。

References)

[1] 張兵, 楊俊, 宋昆侖, 等.大氣污染的危害及其對經濟社會的影響研究——以石家莊市為例[J]. 環境科學與管理, 2015, 40(7): 61-64. (ZAHNG B, YANG J, SONG K L, et al. Harm of air pollution and its impact on economy and society — taking Shijiazhuang city as an example[J]. Environmental Science and Management, 2015, 40(7): 61-64.)

[2] 馬曉燕, 張志紅.PM2.5與哮喘關系的研究進展[J]. 環境與職業醫學, 2015, 32(3): 279-283. (MA X Y, ZHANG Z H. Research progress on association between PM2.5and asthma[J]. Journal of Environmental and Occupational Medicine, 2015, 32(3): 279-283.)

[3] WANG Y, ZHUANG G, ZHANG X, et al. The ion chemistry, seasonal cycle, and sources of PM2.5, and TSP aerosol in Shanghai[J]. Atmospheric Environment, 2006, 40(16): 2935-2952.

[4] 葉文波.寧波市大氣可吸入顆粒物PM10和PM2.5的源解析研究[J]. 環境污染與防治, 2011, 33(9): 66-69. (YE W B. Study on source apportionment of PM10and PM2.5in ambient air of Ningbo[J]. Environmental Pollution and Control, 2011, 33(9): 66-69.)

[5] 賀祥, 林振山. 基于GAM模型分析影響因素交互作用對PM2.5濃度變化的影響[J]. 環境科學, 2017,38(1): 22-32. (HE X, LIN Z S. Interactive effects of the influencing factors on the changes of PM2.5concentration based on gam model[J]. Environmental Science, 2017,38(1): 22-32.)

[6] 湯羹, 馬憲國.上海氣象因素對PM2.5等大氣污染物濃度的影響[J]. 能源研究與信息, 2016, 32(2): 71-74. (TANG G, MA X G. Influence of meteorological conditions in Shanghai on the concentration of PM2.5and other air pollutants[J]. Energy Research and Information, 2016, 32(2): 71-74.)

[7] 張浩月, 王雪松, 陸克定, 等. 珠江三角洲秋季典型氣象條件對O3和PM10污染的影響[J]. 北京大學學報(自然科學版), 2014, 50(3): 565-576. (ZHANG H Y, WANG X S, LU K D, et al. Impact of typical meteorological conditions on the O3and PM10pollution episodes in the Pearl River Delta in autumn[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2014, 50(3): 565-576.)

[8] 王曉彥, 趙熠琳, 霍曉芹, 等. 基于數值模式的環境空氣質量預報影響因素和改進方法[J]. 中國環境監測, 2016, 32(5): 1-7. (WANG X Y, ZHAO Y L, HUO X Q, et al. Discussion on the influence factors and improvement methods of ambient air quality forecasting based on numerical models[J]. Environmental Monitoring in China, 2016, 32(5): 1-7.)

[9] 王茜, 吳劍斌, 林燕芬. CMAQ模式及其修正技術在上海市PM2.5預報中的應用檢驗[J]. 環境科學學報, 2015, 35(6): 1651-1656. (WANG Q, WU J B, LIN Y F. Implementation of a dynamic linear regression method on the CMAQ forecast of PM2.5in Shanghai[J]. Acta Scientiae Circumstantiae, 2015, 35(6): 1651-1656.)

[10] SYRAKOV D, PRODANOVA M, GEORGIEVA E, et al. Simulation of European air quality by WRF-CMAQ models using AQMEII-2 infrastructure[J]. Journal of Computational amp; Applied Mathematics, 2016, 293 (C): 232-245.

[11] ZHANG Y, ZHANG X, WANG L, et al. Application of WRF/Chem over East Asia: part I, model evaluation and intercomparison with MM5/CMAQ[J]. Atmospheric Environment, 2016, 124: 285-300.

[12] 黃思, 唐曉, 徐文帥, 等. 利用多模式集合和多元線性回歸改進北京PM10預報[J]. 環境科學學報, 2015, 35(1): 56-64. (HUANG S, TANG X, XU W S, et al. Application of ensemble forecast and linear regression method in improving PM10forecast over Beijing areas[J]. Acta Scientiae Circumstantiae, 2015, 35(1): 56-64.)

[13] 王占山, 李曉倩, 王宗爽, 等. 空氣質量模型CMAQ的國內外研究現狀[J]. 環境科學與技術, 2013, 36(6): 386-391. (WANG Z S, LI X Q, WANG Z S, et al. Application status of Models-3/CMAQ in environmental management[J]. Environmental Science amp; Technology, 2013, 36(6): 386-391.)

[14] 余輝, 袁晶, 于旭耀, 等. 基于ARMAX的PM2.5小時濃度跟蹤預測模型[J]. 天津大學學報 (自然科學與工程技術版), 2017, 50(1): 105-111. (YU H, YUAN J, YU X Y, et al. Tracking prediction model for PM2.5hourly concentration based on ARMAX[J]. Journal of Tianjin University (Science and Technology), 2017, 50(1): 105-111.)

[15] 彭斯俊, 沈加超, 朱雪.基于ARIMA模型的PM2.5預測[J]. 安全與環境工程, 2014, 21(6): 125-128. (PENG S J, SHEN J C, ZHU X. Forecast of PM2.5based on the arima model[J]. Safety and Environmental Engineering, 2014, 21(6): 125-128.)

[16] 張玉麗, 何玉, 朱家明.基于多元線性回歸模型PM2.5預測問題的研究[J]. 安徽科技學院學報, 2016, 30(3): 92-97. (ZAHNG Y L, HE Y, ZHU J M. Study of the prediction of PM2.5based on the multivariate linear regression model[J]. Journal of Anhui Science and Technology University, 2016, 30(3): 92-97.)

[17] TAI A P K, MICKLEY L J, JACOB D J. Correlations between fine particulate matter (PM2.5) and meteorological variables in the United States: implications for the sensitivity of PM2.5to climate change[J]. Atmospheric Environment, 2010, 44(32): 3976-3984.

[18] 艾洪福, 潘賀, 李迎斌. 關于空氣霧霾PM2.5含量預測優化研究[J]. 計算機仿真, 2017, 34(1): 392-395. (AI H F, PAN H, LI Y B. Research on optimization of PM2.5content prediction in air haze[J]. Computer Simulation, 2017, 34(1): 392-395.)

[19] 戴華煒, 陳小旋, 孫曉通. 基于GM (1, 1) 模型群的深圳市大氣污染物灰色預測[J]. 數學的實踐與認識, 2014, 44(1): 131-136. (DAI H W, CHEN X X, SUN X T. The gray prediction model of the atmospheric pollutants in Shenzhen based on GM (1, 1) [J]. Mathematics in Practice and Theory, 2014, 44(1): 131-136.)

[20] 楊忠, 童楚東, 俞杰, 等. 加權因子的PSO-SVR區域空氣PM2.5濃度預報方法[J]. 計算機應用研究, 2017(2): 405-408. (YANG Z, TONG C D, YU J, et al. Regional PM2.5concentration prediction method of PSO-SVR model with weighting factors[J]. Application Research of Computers, 2017(2): 405-408.)

[21] 李龍, 馬磊, 賀建峰, 等. 基于特征向量的最小二乘支持向量機PM2.5濃度預測模型[J]. 計算機應用, 2014, 34(8): 2212-2216. (LI L, MA L, HE J F, et al. PM2.5concentration prediction model of least squares support vector machine based on feature vector[J]. Journal of Computer Applications, 2014, 34(8): 2212-2216.)

[22] 葛考, 時貝貝, 徐康耀, 等.基于BAPSO-PNN神經網絡算法的空氣質量評價研究[J]. 環境工程, 2015, 33: 676-681. (GE K, SHI B B, XU K Y, et al. Air quality assement based on BAPSO-PNN neural network algorithm [J]. Environmental Engineering, 2015, 33: 676-681.)

[23] 楊云, 付彥麗.基于T-S模型模糊神經網絡的PM2.5質量濃度預測[J]. 陜西科技大學學報, 2015, 33(6): 162-166. (YANG Y, FU Y L. The prediction of mass concentration of PM2.5based on T-S fuzzy neural network[J]. Journal of Shaanxi University of Science and Technology, 2015, 33(6): 162-166.)

[24] 馬天成, 劉大銘, 李雪潔, 等.基于改進型PSO的模糊神經網絡PM2.5濃度預測[J]. 計算機工程與設計, 2014, 35(9): 3258-3262. (MA T C, LIU D M, LI X J, et al. Improved particle swarm optimization based fuzzy neural network for PM2.5concentration prediction[J]. Computer Engineering and Design, 2014, 35(9): 3258-3262.)

[25] 荊濤, 李霖, 于文柱, 等.t分布受控遺傳算法優化BP神經網絡的PM2.5質量濃度預測[J]. 中國環境監測, 2015, 31(4): 100-105. (JIN T, LI L, YU W Z, et al. Prediction of PM2.5mass concentration based on BP neural network optimized by t-distribution controlled genetic algorithm[J]. Environmental Monitoring in China, 2015, 31(4): 100-105.)

[26] 謝超, 馬民濤, 于肖肖.多種神經網絡在華北西部區域城市空氣質量預測中的應用[J]. 環境工程學報, 2015, 9(12): 6005-6009. (XIE C, MA M T, YU X X. Forecasting model of air pollution index based on multi-artificial neural network in western region of Northern China[J]. Chinese Journal of Environmental Engineering, 2015, 9(12): 6005-6009.)

[27] 李嵩, 王冀, 張丹闖, 等. 大氣PM2.5污染指數預測優化模型仿真分析[J]. 計算機仿真, 2015, 32(12): 400-403. (LI S, WANG J, ZHANG D C, et al. Simulation analysis of prediction optimization model for atmospheric PM2.5pollution index[J]. Computer Simulation, 2015, 32(12): 400-403.)

[28] MISHRA D, GOYAL P, UPADHYAY A. Artificial intelligence based approach to forecast PM2.5, during haze episodes: a case study of Delhi, India[J]. Atmospheric Environment, 2015, 102: 239-248.

[29] HAYKIN S. Neural Networks: a Comprehensive Foundation [M]. 2rd ed. Upper Saddle River, NJ: Prentice Hall Press, 1998.

[30] BISHOP C M. Neural Networks for Pattern Recognition[M]. Oxford: Oxford University Press, 1995.

[31] ZHANG G, PATUWO B E, HU M Y. Forecasting with artificial neural networks: the state of the art[J]. International Journal of Forecasting, 1998, 14(1): 35-62.

[32] 樓文高, 王延政.基于BP網絡的水質綜合評價模型及其應用[J]. 環境工程學報, 2003, 4(8): 23-26. (LOU W G, WANG Y Z. Water quality comprehensive assessment model using BP networks and its applications[J]. Chinese Journal of Environmental Engineering, 2003, 4(8): 23-26.)

[33] 樓文高.實現BP神經網絡從理論到實踐的跨越[J]. 哈爾濱工程大學學報, 2006, 27: 59-63. (LOU W G. Realization of BP neural network from theory to practice[J]. Journal of Harbin Engineering University, 2006, 27: 59-63.)

[34] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46-61.

[35] MIRJALILI S. How effective is the grey wolf optimizer in training multi-layer perceptrons[J]. Applied Intelligence, 2015, 43(1): 150-161.

[36] 葛躍, 王明新, 孫向武, 等. 基于增強回歸樹的城市PM2.5日均值變化分析: 以常州為例[J]. 環境科學, 2017, 38(2): 485-494. (GE Y, WANG M X, SUN X W, et al. Variation analysis of daily PM2.5concentrations based on boosted regression tree: a case study in Changzhou[J]. Environmental Science, 2017, 38(2): 485-494.)

[37] HECHT-NIELSEN R. Theory of the backpropagation neural network [M]// WECHSLER H. Neural Networks for Perception. New York: Academic Press, 1991: 65-93.

[38] 樓文高, 喬龍. 基于神經網絡的金融風險預警模型及其實證研究[J]. 金融論壇, 2011(11): 52-61. (LOU W G, QIAO L. Early warning model of financial risks and empirical study based on neural network[J]. Finance Forum, 2011(11): 52-61.)

[39] DOMBI G W, NANDI P, SAXE J M, et al. Prediction of rib fracture injury outcome by an artificial neural network [J]. Journal of Trauma, 1995, 39(5): 915-921.

NeuralnetworkmodelforPM2.5concentrationpredictionbygreywolfoptimizeralgorithm

SHI Feng1, LOU Wengao1,2, ZHANG Bo3*

(1.SchoolofOptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China;2.InformationandComputerFaculty,ShanghaiBusinessSchool,Shanghai200235,China;3.CollegeofCommunicationandArtDesign,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

Focusing on high cost and complicated process of the fine particulate matter (PM2.5) measurement system, a neural network model based on grey wolf optimizer algorithm was established. From the perspective of non-mechanism model, the daily PM2.5concentration in Shanghai was forecasted with meteorological factors and air pollutants, and the important factors were analyzed by mean impact value. To avoid the “over training” and ensure the generalization ability, the validation datasets were used to monitor the training process. The experimental results show that the most significant factors that affecting the PM2.5concentration are PM10, and then are the CO and the previous day’s PM2.5. Based on the datasets obtained from November 1, 2016 to November 12, the relative average error of the proposed model is 13.46%, the absolute average error is 8 μg/m3; the relative average error of it is decreased by about 3 percentage points, 5 percentage points and 1 percentage points compared with the prediction models based on Particle Swarm Optimization (PSO), BP neural network and Support Vector Regression (SVR). The neural network model based on the grey wolf optimizer algorithm is more suitable for forecasting PM2.5concentration and air quality in Shanghai.

grey wolf optimizer algorithm; BP neural network; PM2.5concentration prediction; prediction model; air pollutant

2017- 04- 20;

2017- 06- 22。

上海高校知識服務平臺“上海市商貿服務業知識項目服務中心”建設項目(ZF1226)。

石峰(1992—),男,河南南陽人,碩士研究生,主要研究方向:人工神經網絡、數據挖掘; 樓文高(1964—),男,浙江杭州人,教授,博士,主要研究方向:金融工程、商務經濟學、人工神經網絡、數據挖掘; 張博(1979—),男,天津人,副教授,博士,CCF會員,主要研究方向:網絡新媒體、數字出版。

1001- 9081(2017)10- 2854- 07

10.11772/j.issn.1001- 9081.2017.10.2854

TP183; TP181;X823

A

This work is partially supported by the Construction Program of Shanghai Trade Service Knowledge Service Center in Shanghai University Knowledge Service Platform (ZF1226).

SHIFeng, born in 1992, M. S. candidate. His research interests include artificial neural networks, data mining.

LOUWengao, born in 1964, Ph. D., professor. His research interests include finance engineering, economics business, data mining.

ZHANGBo, born in 1979, Ph. D., associate professor. His research interests include network new media, digital publishing.