融合深度置信網絡與與核極限學習機算法的核磁共振測井儲層滲透率預測方法

朱林奇,張 沖,周雪晴,魏 旸,黃雨陽,高齊明

(1.油氣資源與勘探技術教育部重點實驗室(長江大學),武漢 430100; 2.長江大學 地球物理與石油資源學院,武漢 430100) (*通信作者電子郵箱yzlogging@163.com)

融合深度置信網絡與與核極限學習機算法的核磁共振測井儲層滲透率預測方法

朱林奇1,2,張 沖1,2*,周雪晴1,2,魏 旸1,2,黃雨陽1,2,高齊明1,2

(1.油氣資源與勘探技術教育部重點實驗室(長江大學),武漢 430100; 2.長江大學 地球物理與石油資源學院,武漢 430100) (*通信作者電子郵箱yzlogging@163.com)

由于低孔低滲儲層孔隙結構較為復雜,現有核磁共振(NMR)測井滲透率模型對于低孔低滲儲層預測精度不高。為此,提出一種融合深度置信網絡(DBN)算法與核極限學習機(KELM)算法的滲透率預測方法。該方法首先對DBN模型進行預訓練,然后將KELM模型作為預測器放置在訓練好DBN模型后,利用訓練數據進行有監督的訓練,最終形成深度置信-核極限學習機(DBKELMN)模型。考慮到該模型需充分利用反映孔隙結構的橫向弛豫時間譜信息,將離散化后的核磁共振測井橫向弛豫時間譜作為輸入,滲透率作為輸出,確定NMR測井橫向弛豫時間譜與滲透率的函數關系,并基于該函數關系對儲層滲透率進行預測。實例應用表明,融合DBN算法與KELM算法的滲透率預測方法是有效的,預測樣本的平均絕對誤差(MAE)較斯倫貝謝道爾研究中心(SDR)模型降低了0.34。融合DBN算法與KELM算法的滲透率預測方法可提高低孔滲儲層滲透率預測精度,可應用于油氣田勘探開發。

深度學習;核磁共振測井;滲透率;深度置信網絡;深度置信-核極限學習機

0 引言

由于低孔滲儲層存在較致密、非均質性強的特點,導致儲層滲透率較小,常規測井難以準確預測。核磁共振測井測量得到的橫向弛豫時間譜(T2譜)中存在的孔隙結構信息十分豐富,所以,如何利用T2譜的豐富孔隙結構信息,是預測儲層滲透率精度的關鍵。

核磁共振測井滲透率模型可以分為三類：將橫向弛豫時間譜(T2譜)分區間與滲透率建立統計關系或理論關系的模型[1-2];斯倫貝謝道爾研究中心(Schlumberger Doll Researchcenter, SDR)模型及其改進模型[3];與壓汞資料結合,利用各種孔隙結構計算滲透率的模型[4-10]。前兩種模型均嘗試用一個參數或幾個參數描述整個T2譜的形態變化,在低孔滲儲層中,孔隙結構復雜,T2譜的變化較大,較少的參數難以表征這種變化。第三種模型未考慮儲層含油氣對T2譜形態的影響,將這種影響也看作對孔隙結構變化的響應,導致在油氣層滲透率預測不準。上述三種模型均存在不適應于低孔滲儲層滲透率預測的情況。

針對上述問題,本文將T2譜作為輸入,滲透率作為輸出,利用本文提出的深度置信-極限學習機網絡(Deep Belief Kernel Extreme Learning Machine Network, DBKELMN)進行函數的映射,以確定T2譜與滲透率的函數關系并預測儲層滲透率,達到準確預測滲透率的目的。

1 深度置信-核極限學習機模型

考慮到輸入曲線維數高(對于斯倫貝謝儀器,T2譜由30維或64維數據組成)、模型復雜度強、含氣矯正較為困難,提出了利用深度學習方法對模型進行學習。深度學習理論認為,淺層學習算法包括極限學習機(Extreme Learning Machine, ELM)、支持向量機(Support Vector Machine, SVM)、反向傳播神經網絡(Back Propagation Neural Network, BPNN)、徑向基函數神經網絡(Radial Basis Function Neural Network, RBFNN)，由于隱層數過少導致難以表征較為復雜的函數關系；而深度學習模型由于能進行逐層特征提取,具有強特征提取能力,對復雜函數具有強大的學習能力。但是,在石油勘探領域中,深度學習算法還未引起重視。本文利用其抽象數據特征的能力進行高維數據的降維，利用其自動特征提取功能進行含氣校正，利用其多隱層的特征進行復雜非線性滲透率模型的學習,以期準確預測滲透率。

1.1 深度置信網絡

深度置信網絡(Deep Belief Network, DBN)是一種半監督學習算法,解決了深度神經網絡難以優化的問題[11]。它由多層隨機隱變量組成，其最底層單元的狀態為輸入曲線,向上連接若干限制玻爾茲曼機(Restricted Boltzmann Machine, RBM)堆棧。訓練時先輸入若干維樣本進行第一層RBM的訓練,并利用訓練結果作為輸入進行下一層RBM的訓練,以此類推逐層進行RBM的預訓練,最后利用誤差反向傳播算法去微調整個網絡參數。RBM是一種特殊的玻爾茲曼機,其對輸入層與隱層連接進行了限制,僅連接了輸入層節點與隱層節點[12],如圖1所示。假設所有輸入曲線v和隱單元h均為二值變量,即對于任意ij,均有vi∈{0,1},hj∈{0,1}。對于一組給定的節點(v,h),RBM系統定義能量函數:

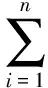
(1)

其中:θ={Wij,bi,cj}為RBM模型參數。基于該能量函數得到(v,h)的聯合概率分布為:

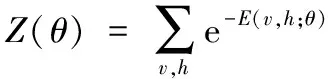
(2)

其中Z(θ)稱為歸一化因子。

輸入曲線層的邊際分布為:

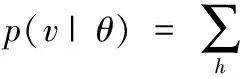
(3)

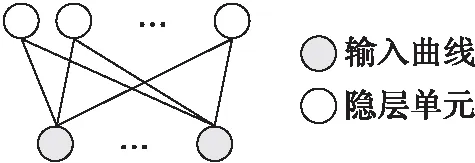
圖1 RBM示意圖

由于RBM的特殊結構,可得到第j個隱單元的激活概率為:

苗木的生存離不開相應的監督，在管理上，需要培養技術人員掌握相應的育苗和管理技能。同時，在培訓中應補充相應的技術實踐，使他們能夠更好地掌握林木育苗技術，使造林更加符合我國的建設。林業標準在苗木培育技術管理上應引進相關新技術，提高我國造林苗木培育技術水平，在苗木的日常管理和保護上，應做到不間斷監測，及時滿足。苗木對水肥的需求，保證了苗木生長發育過程中的養分需求。同時，創新育苗方法，確保苗木成活率，從而保證我國林業育種的順利實施，同時為我國人工造林事業做出貢獻。

(4)

其中σ為sigmoid激活函數。

第i個可見單元的激活概率為:

(5)

利用式(4)計算隱層單元狀態,進而利用式(5)確定可見單元vi取值為1的概率,進而產生可見層的重構。本文即是利用該方法進行RBM的模型訓練。

1.2 核極限學習機

利用誤差反向傳播算法進行求解，其解有可能為局部極小解，而不是全局最優解，導致預測精度會受到影響,即使存在預學習的方法,仍無法徹底解決該問題。為此,本文嘗試將核ELM(Kernel ELM, KELM)作為預測器連接于DBN后,提高預測精度。KELM結合了ELM的學習精度及計算效率的優勢及核方法處理非線性不可分問題的優勢,是一種高效可靠的淺層模型,其性能優于BPNN、SVM及ELM[13]。

對于數據集D={xp,tp},xp為輸入,tp為目標輸出,那么,對于隱層節點數為L的ELM,有輸出:

(6)

其中:β=[β1,β2,…,βL]T,為ELM隱層與輸出層的權值向量;h(xp)=[h1(xp),h2(xp),…,hL(xp)]T為xp從n維輸入空間映射到L維隱層特征空間的向量。那么,根據KKT(Karush-Kuhn-Tucker)理論可知,ELM訓練等同求解一對偶優化,即:

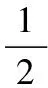
(7)

其中:C為正則化系數;ζp為理論輸出tp相對于實際輸出f(xp)的誤差;αp為Lagrange乘子。求解式(7),可得:

(8)

其中:T=[t1,t2,…,tN]T為輸入樣本的目標值向量。將式(8)代入式(6)得模型的輸出為:

f(xp)=[K(xp,x1),K(xp,x2),…,K(xp,xN)]·

(I/C+HHT)-1T

(9)

其中K為核函數。由式(9)可以看到,模型輸出結果與隱層數無關,即KELM在使用中無需設定隱層數,避免了模型確定時隱層數選擇的盲目性。本文在進行建模時,選用較為普遍的高斯核為算法中的核函數。

1.3 基于DBKELMN的NMR測井預測滲透率方法

基于上述特點,本文嘗試將DBN與KELM結合,提出了DBKELMN模型,提升模型的穩定性、精度及泛化能力。在模型建立時,首先提取核磁共振測井T2譜數據及對應的滲透率,如圖2所示。其中,核磁共振測井T2譜原始數據一般已被離散化為30維或64維的數據,利用離散化后的數據中孔隙度分量值作為T2譜的輸入數據(由于采樣時間點固定,在選取輸入樣本的特征時,可忽略采樣時間值,僅輸入孔隙度分量)。

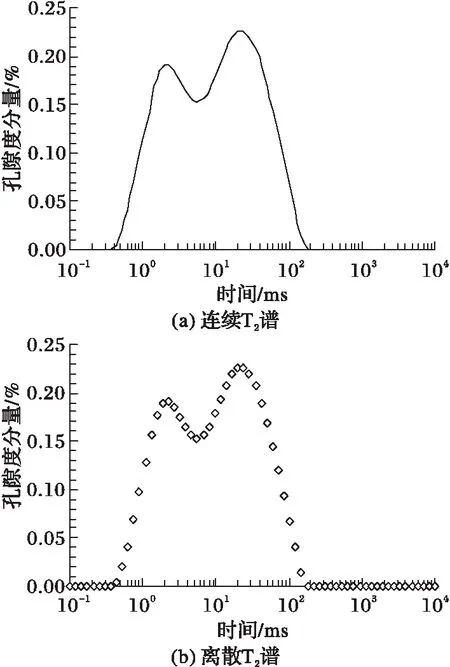
圖2 T2譜離散化示意圖

然后利用輸入數據逐層對RBM進行預訓練,建立特征抽象層。將特征抽象層建立好之后,將離散化T2譜輸入,并將特征抽象層對應的輸出作為特征,輸入到核極限學習機中,利用KELM中的核函數對特征進行映射,并通過KELM網絡,得到最終輸出,而不進行參數的微調。借助DBN中的特征抽象層優勢,使得模型的特征提取能力更強,對復雜函數的逼近能力更強。而KELM網絡較快的訓練速度,以及較其他模型更強的泛化能力,顯著提高了DBKELM的適用性,如圖3所示。在第2章中,本文將通過某區塊致密氣儲層資料證明該模型在精度與泛化能力的優勢。

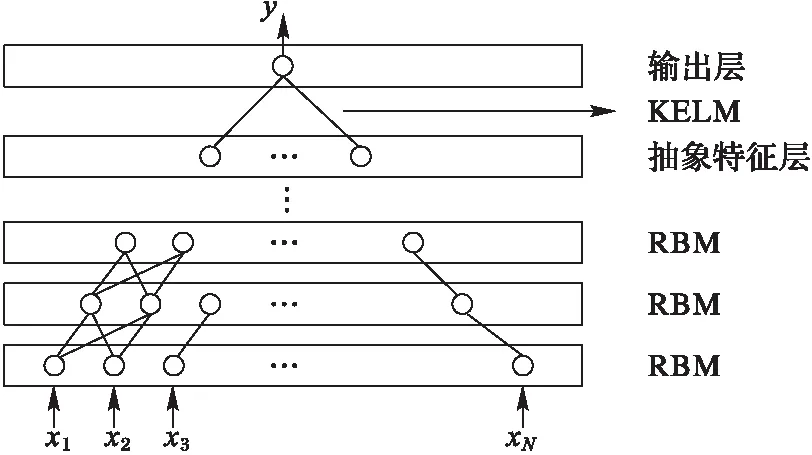
圖3 DBKELMN示意圖

2 實例與分析

為了證明深度學習算法的有效性,利用某區致密氣儲層資料進行模型的驗證。利用9口井320塊巖樣進行絕對滲透率的測定并提取對應深度核磁共振測井T2譜。其中,將7口井200塊巖樣數據設為訓練樣本,另2口井(A1、A2) 塊巖樣數據設為預測樣本。將數據進行歸一化之后,分別嘗試建立KELM、DBN模型與DBKELMN模型。本文采用K交叉驗證(K-Cross Validation,K-CV)方法進行交叉驗證,以有效避免過學習及欠學習的發生[14]。將200個訓練樣本均分為4組,每組數據分別作1次驗證集,除此組以外的數據作為訓練集。對DBN與KELM模型采用K折交叉驗證(K-CV),確定兩模型的最優參數。最后確定的最適合于預測滲透率的KELM網絡參數為:正則化系數2-2,核參數240;確定的DBN網絡參數為:隱層數20、隱層神經元數30。隱層數與隱層神經元數較大的原因應歸結為滲透率與T2譜關系復雜,所以需要高隱層數去進行表征。

同樣,在DBKELMN網絡中,隱層數、不同的正則化系數C與核參數γ共同決定了網絡的精度(相對于隱層數來說神經元數與精度相關性弱,所以該處取DBN模擬得到的最優隱層神經元數30進行模擬)。通過對200樣本進行K-CV模擬,確定不同網絡參數對預測精度的影響大小見圖4。通過圖4可以看出,網絡參數的改變對精度的改變并不大。隨著正則化系數C的變大,網絡的穩定性逐漸變強;而隨著核參數γ的增大,當大于2-6時,網絡精度提升;而隱層數的變化與網絡精度相關性很小,存在隱層數大、精度變高的情況,但是并不明顯。根據模擬結果,認為在該模型中,正則化系數C等于215,核參數γ等于215,隱層數為15時,模型的泛化能力最好,預測精度最高。為了方便進行對比,同時建立正則化系數不變、核參數不變、隱層數1、2、3、5、10層的模型,并對預測樣本進行處理,以觀察模型的效果。

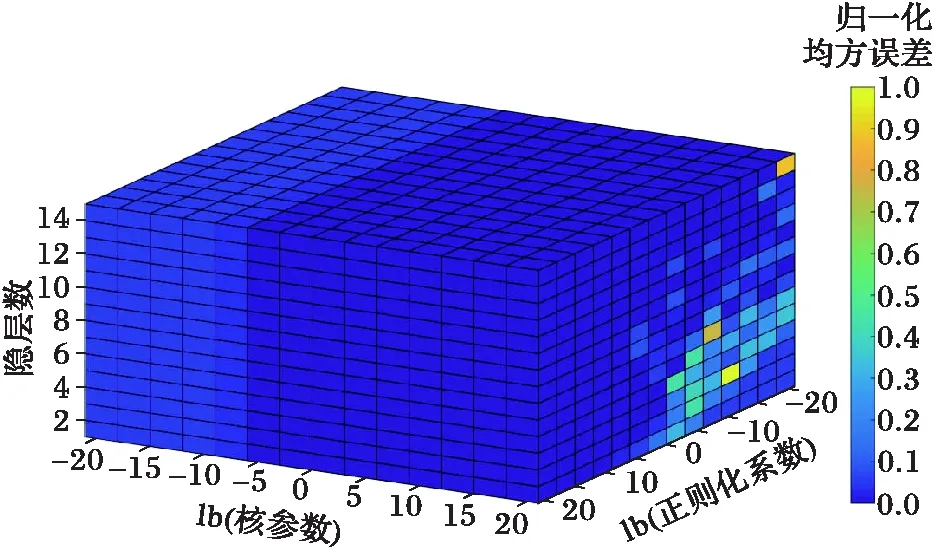
圖4 DBKELMN模型正則化系數C-核參數γ歸一化誤差體

同時,建立1隱層20隱層單元的BPNN模型以及由1 000個C4.5算法組成的隨機森林(Random Forest, RF)模型同時進行學習,并通過巖心數據確定SDR模型以及Coates模型系數，通過該儲層驗證井的預測精度高低評價模型的優劣。對A1井及A2井的120個預測樣本評價結果如圖5所示。

由圖5來看,Timur模型與SDR模型明顯對低孔滲儲層滲透率預測能力不足,這也是由于未考慮過多的儲層微觀參數所必然造成的結果。RF模型預測效果略好于其他淺層學習算法(BPNN模型、KELM模型),說明對于地球物理問題來說,集成算法能在一定程度上提高泛化能力,而DBN模型效果是略優于其他模型的。從圖6來看,本文提出的深度模型框架,在參數合適的情況下,預測精度是高于淺層模型的。比較2種深度學習模型評價結果,可以看出,DBKELMN的泛化能力是優于DBN的,預測精度較高,如果利用集成算法進行集成,精度有可能會進一步提高,該思路可作為下一步研究方向。同時也可以看出,15層網絡模型的效果要優于其他模型。這是由于地球物理問題的特殊性所導致的,地球物理問題雖由于成本的原因導致輸入維數與樣本數較小,但是輸入曲線與輸出關系復雜,且存在對應的物理關系,所以即使模型層數較高,精度也并不會降低,反而是需要較多層數來表征復雜的函數關系。對應的A1、A2井不同模型預測平均絕對誤差(Mean Absolute Error, MAE)結果統計見表1。

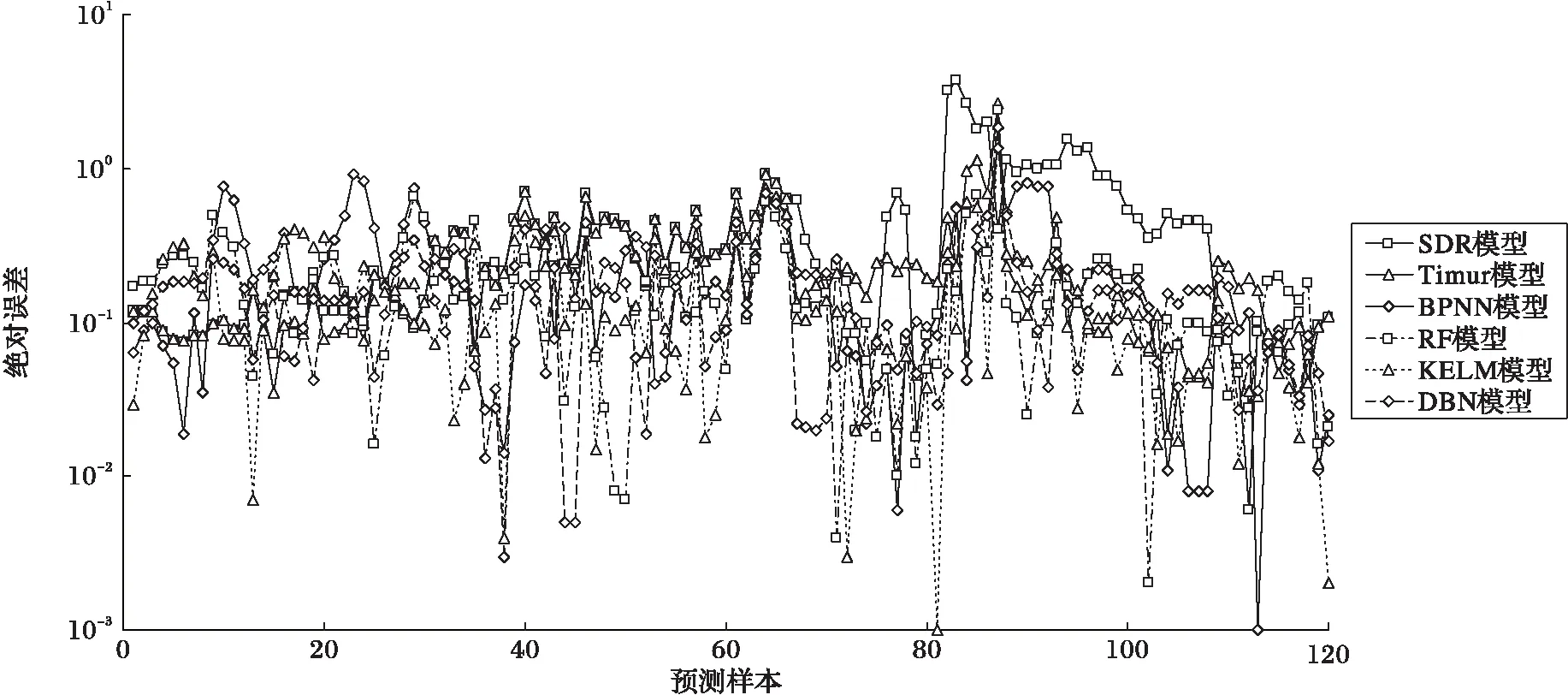
圖5 不同模型對預測樣本的預測絕對誤差

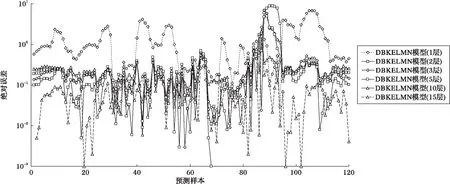
圖6 不同隱層下DBKELMN模型對預測樣本的預測絕對誤差

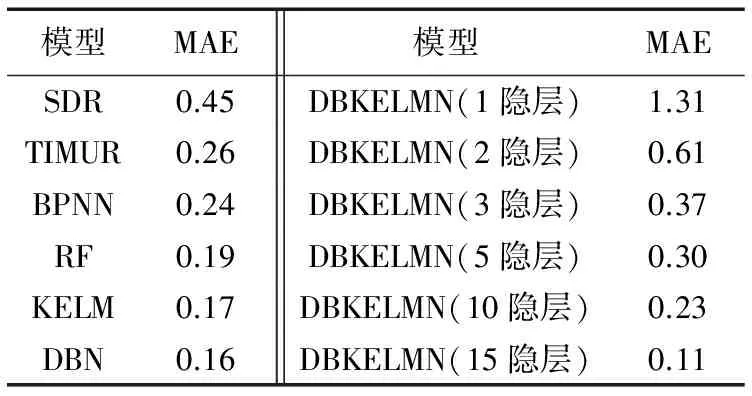
表1 不同模型預測MAE結果

從表1可以得出,在MAE指標上,DBKELMN模型得到的結果均優于其他模型,多層網絡的確能增加模型的精度。上述分析表明,DBKELMN模型預測精度優于其他模型,可應用于對致密砂巖儲層滲透率預測。

3 結語

針對現有滲透率模型對核磁共振測井信息利用率不足導致的預測精度不高的問題,本文提出了將T2譜作為輸入,滲透率作為輸出,利用函數逼近算法確定T2譜與滲透率的函數關系。該方法可準確預測低孔滲儲層滲透率。同時,將DBN模型與KELM模型進行融合,提出了DBKELMN模型,以原有模型改進訓練速度與泛化能力的問題,使其更適合于儲層滲透率評價。在今后的工作中,應主要針對深度學習算法在各類測井解釋問題的適用性以及模型對樣本數量的需求進行研究,使深度學習模型能更好地為測井解釋問題提供幫助。

References)

[1] 邵維志, 解經宇, 遲秀榮, 等.低孔隙度低滲透率巖石孔隙度與滲透率關系研究[J]. 測井技術, 2013, 37(2): 149-153. (SHAO W Z, XIE J Y, CHI X R, et al. On the relation of porosity and permeability in low porosity and low permeability rock [J]. Well Logging Technology, 2013, 37(2): 149-153.)

[2] PETROBRAS T W, PETROBRAS C B, PETROBRAS N P, et al. Magnetic Resonance (NMR) approach for permeability estimation in carbonate rocks [EB/OL]. [2017- 01- 10]. https://www.onepetro.org/conference-paper/OTC-26338-MS.

[3] XIAO L, ZOU C C, MAO Z Q, et al. Tight-gas-sand permeability estimation from Nuclear-Magnetic-Resonance (NMR) logs based on the Hydraulic-Flow-Unit (HFU) approach [EB/OL]. [2017- 01- 10]. https://www.onepetro.org/journal-paper/SPE-167255-PA.

[4] XIAO L, LIU X P, ZOU C C, et al. Comparative study of models for predicting permeability from Nuclear Magnetic Resonance (NMR) logs in two Chinese tight sandstone reservoirs [J]. Acta Geophysica, 2014, 62(1): 116-141.

[5] RIOS E H, AZEREDO R B V, MOSS A K, et al. Estimating the permeability of carbonate rocks by principal component regressions of NMR and MICP data [C]// Proceedings of the SPWLA 56th Annual Logging Symposium. Long Beach, CA: [s.n.], 2015.

[6] WEI D F, LIU X P, HU X X, et al. Estimation of permeability from NMR logs based on formation classification method in tight gas sands [J]. Acta Geophysica, 2015, 63(5): 1316-1338.

[7] 成志剛, 羅少成, 杜支文, 等.基于儲層孔喉特征參數計算致密砂巖滲透率的新方法[J]. 測井技術, 2014, 38(2): 185-189. (CHENG Z G, LUO S C, DU Z W, et al. The method to calculate tight sandstone reservoir permeability using pore throat characteristic parameters [J]. Well Logging Technology, 2014, 38(2): 185-189.)

[8] RUSH D, LINDSAY C, ALLEN M. Combining electrical measurements and mercury porosimetry to predict permeability [J]. Petrophysics, 2013, 54(6): 531-537.

[9] 朱林奇, 張沖, 何小菊, 等.基于動態孔隙結構效率的核磁共振測井預測滲透率方法[J]. 新疆石油地質, 2015, 36(5): 607-611. (ZHU L Q, ZHANG C, HE X J, et al. NMR logging permeability prediction method based on dynamic pore structure efficiency [J]. Xinjiang Petroleum Geology, 2015, 36(5): 607-611.)

[10] 朱林奇, 張沖, 胡佳, 等.基于單元體模型的核磁共振測井滲透率評價方法[J]. 石油鉆探技術, 2016, 44(5): 120-126. (ZHU L Q, ZHANG C, HU J, et al. An NMR logging permeability evaluation method based on the representative elementary volume model [J]. Petroleum Drilling Techniques, 2016, 44(5): 120-126.)

[11] HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks [J]. Science, 2006, 313(5786): 504-507.

[12] HINTON G E. Training products of experts by minimizing contrastive divergence [J]. Neural Computation, 2002, 14(8): 1771-1800.

[13] HUANG G B, ZHOU H M, DING X J. Extreme learning machine for regression and multiclass classification [J]. IEEE Transactions on Systems, Man, and Cybernetics, 2013, 43(2): 513-529.

[14] 江沸菠, 戴前偉, 董莉.基于主成分-正則化極限學習機的超高密度電法非線性反演[J]. 地球物理學報, 2015, 58(9): 3356-3369. (JIANG F B, DAI Q W, DONG L. Ultra-high density resistivity nonlinear inversion based on principal component-regularized ELM [J]. Chinese Journal of Geophysics, 2015, 58(9): 3356-3369.)

Nuclearmagneticresonanceloggingreservoirpermeabilitypredictionmethodbasedondeepbeliefnetworkandkernelextremelearningmachinealgorithm

ZHU Linqi1,2, ZHANG Chong1,2*, ZHOU Xueqing1,2,WEI Yang1,2, HUANG Yuyang1,2, GAO Qiming1,2

(1.KeyLaboratoryofExplorationTechnologiesforOHandGasResourcesofMinistryofEducation(YangtzeUniversity),WuhanHubei430100,China;2.SchoolofGeophysicsandOilResources,YangtzeUniversity,WuhanHubei430100,China)

Duing to the complicated pore structure of low porosity and low permeability reservoirs, the prediction accuracy of the existing Nuclear Magnetic Resonance (NMR) logging permeability model for low porosity and low permeability reservoirs is not high. In order to solve the problem, a permeability prediction method based on Deep Belief Network (DBN) algorithm and Kernel Extreme Learning Machine (KELM) algorithm was proposed. The pre-training of DBN model was first carried out, and then the KELM model was placed as a predictor in the trained DBN model. Finally, the Deep Belief Kernel Extreme Learning Machine Network (DBKELMN) model was formed with supervised training by using the training data. Considering that the proposed model should make full use of the information of the transverse relaxation time spectrum which reflected the pore structure, the transverse relaxation time spectrum of NMR logging after discretization was taken as the input, and the permeability was taken as the output. The functional relationship between the transverse relaxation time spectrum of NMR logging and permeability was determined, and the reservoir permeability was predicted based on the functional relationship. The applications of the example show that the permeability prediction method based on DBN algorithm and KELM algorithm is effective and the Mean Absolute Error (MAE) of the prediction sample is 0.34 lower than that of Schlumberger Doll Researchcenter (SDR) model. The experimental results show that the combination of DBN algorithm and KELM algorithm can improve the prediction accuracy of low porosity and low permeability reservoir, and can be used to the exploration and development of oil and gas fields.

Deep Learning (DL); Nuclear Magnetic Resonance (NMR) logging; permeability; Deep Belief Network (DBN); Deep Belief Kernel Extreme Learning Machine Network (DBKELMN)

2017- 04- 02;

2017- 05- 20。

湖北省自然科學基金資助項目(2013CFB396);中國石油天然氣集團公司重大專項(2013E- 38- 09);長江大學教育部實驗室開放基金資助項目(K2016- 09)。

朱林奇(1993—),男,湖北荊州人,博士研究生,CCF會員,主要研究方向:機器學習與數據挖掘方法的地球物理應用、核磁共振測井解釋; 張沖(1983—),男,湖北漢川人,副教授,博士,主要研究方向:復雜儲層測井解釋; 周雪晴(1993—),女,山東東營人,碩士研究生,主要研究方向:測井地質、機器學習與數據挖掘方法的地球物理應用; 魏旸(1991—),男,湖北孝感人,碩士研究生,主要研究方向:碳酸鹽巖測井解釋; 黃雨陽(1994—),男,湖北鄂州人,碩士研究生,主要研究方向:頁巖氣測井解釋; 高齊明(1990—),男,山東泰安人,碩士,主要研究方向:測井解釋。

1001- 9081(2017)10- 3034- 05

10.11772/j.issn.1001- 9081.2017.10.3034

TP18;P631.8

A

This work is partially supported by the Natural Science Foundation of Hubei Province (2013CFB396), the Major Projects of China National Petroleum Corporation (2013E- 38- 09), the Open Found of Key Laboratory of Exploration Technologies for Oil and Gas Resources (Yangtze University), Ministry of Education (K2016 09).

ZHULinqi, born in 1993, Ph. D. candidate. His research interests include machine learning and data mining application in geophysics, nuclear magnetic resonance logging interpretation.

ZHANGChong, born in 1983, Ph. D., associate professor. His research interests include complex reservoir well logging interpretation.

ZHOUXueqing, born in 1993, M. S. candidate. Her research interests include logging geology, machine learning and data mining application in geophysics.

WEIYang, born in 1991, M. S. candidate. His research interests include carbonate logging interpretation.

HUANGYuyang, born in 1994, M. S. candidate. His research interests include shale gas logging interpretation.

GAOQiming, born in 1990, M. S. His research interests include logging interpretation.