二項式定理題型掃描

湖北 廖慶偉

二項式定理題型掃描

湖北 廖慶偉

二項式定理是高考必考的，常考題型是選擇題或填空題，屬容易題或中等題，二項式定理常考題型如下.

一、求常數項

( )

( )

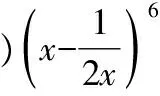
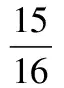
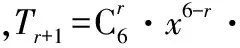
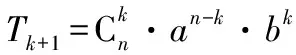
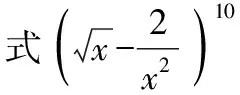
A.360 B.180 C.90 D.45

( )

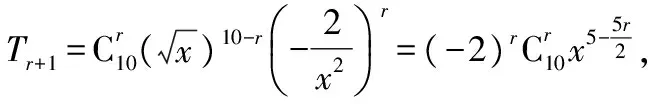
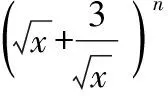
A.6 B.9 C.12 D.18

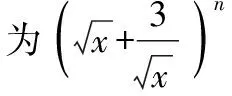
二、求指定項的系數

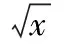
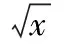
點評：求二項展開式的指定項的系數問題，一般是利用通項公式進行化簡后，令字母的指數符合要求，解出Tr+1中的r，再代回通項公式即可.注意求指定項的系數與求指定項是不同的.

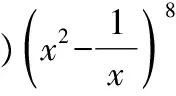
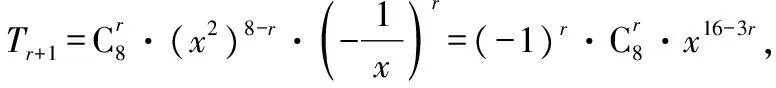
【變式2】(2017·山西大學附中高三二模測試)(x-2y)6的展開式中，x4y2的系數為

( )

A.15 B.-15 C.60 D.-60

( )

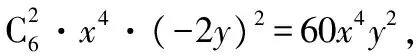
A.-4 B.-2 C.2 D.4

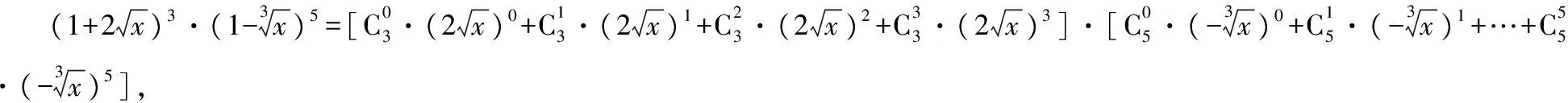
三、求指定項

【例3】(2016·四川理)設i為虛數單位，則(x+i)6的展開式中含x4的項為

( )

A.-15x4B.15x4C.-20ix4D.20ix4

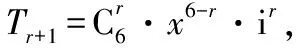
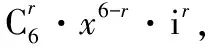
【變式1】設i為虛數單位，則(x-i)6的展開式中含x4的項為

( )

A.-15x4B.15x4C.-20ix4D.20ix4

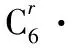
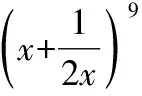
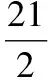
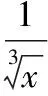
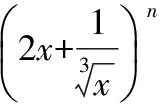
四、求有理項

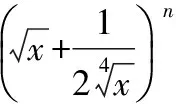
點評：求二項展開式的有理項問題一般是利用通項公式進行，化簡通項公式后，令字母的指數為整數，解出Tr+1中的r，注意0≤r≤n,r,n∈N，再代回通項公式即可.

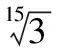
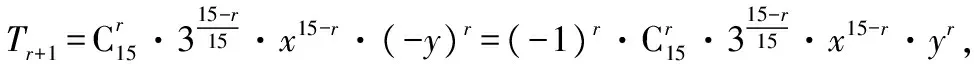
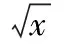
A.2 B.3 C.4 D.5

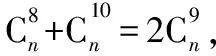
五、求參數的值

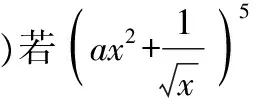
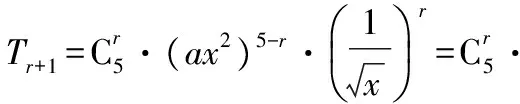
點評：二項式定理中的求參數問題，一般是利用通項公式進行化簡后，令字母的指數符合要求，解出Tr+1中的r，再代回通項公式即可.

( )

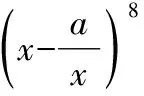
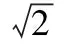
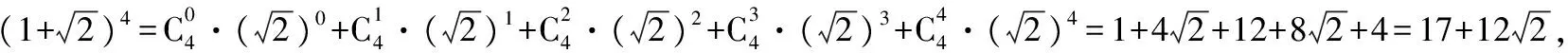
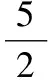
隨著燃料乙醇和食品加工中伴生的液體副產品產量增加、果蔬種植規模化伴生的鮮基飼用資源增加，加上環保要求趨嚴、飼料成本上升，促進了液體農副產品、鮮基地源飼料和發酵液體飼料的應用和推廣，液體飼料具有廣闊的發展前景[1]。

( )

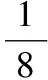
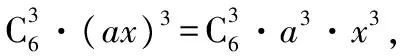
六、求展開式系數和

【例5】已知(x2-3x+1)5=a0+a1x+a2x2+…+a10x10，則a1+a2+a3+…+a10=

( )

A.-1 B.1 C.-2 D.0

【解析】因為(x2-3x+1)5=a0+a1x+a2x2+…+a10x10，令x=0，可得a0=1，令x=1,可得a0+a1+a2+…+a10=-1，所以a1+a2+…+a10=-2,故選C.

點評：求解本題應先令x=0，求a0，再令x=1，求a0+a1+a2+…+a10，最后求a1+a2+a3+…+a10.用二項式定理展開時，要注意按字母x的指數從小到大或從大到小排列. 同時應注意二項式系數的規律.

【變式1】若(1+x)(1-2x)7=a0+a1x+a2x2+…+a8x8，則a1+a2+…+a7的值是

( )

【答案】C 【解析】由題意可知a8=(-2)7=-128，令x=0得a0=1，令x=1得a0+a1+a2+…+a7+a8=-2，所以a1+a2+…+a7=125，故選C.

【變式2】已知展開式中第4項與第8項的二項式系數相等，則奇數項的二項式系數和為

( )

A.212B.211C.210D.29

( )

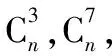
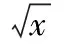
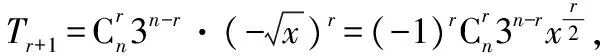
【變式4】設(2-x)6=a0+a1x+a2x2+…+a6x6，則 |a1|+|a2|+…+|a6|的值是

( )

A.729 B.665 C.728 D.636

【答案】B 【解析】令x=0,則a0=26=64,而(2+x)6=a0+|a1|x+|a2|x2+…+|a6|x6,令x=1可得a0+|a1|+|a2|+…+|a6|=36=729,故|a1|+|a2|+…+|a6|=729-64=665,故選B.

七、求最值

( )

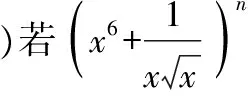
A.3 B.4 C.5 D.6

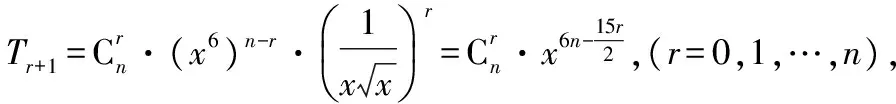
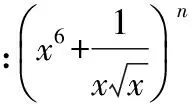
【變式1】已知 (x+1)2012=a1+a2x+a3x2+…+a2013x2012，若數列a1,a2,a3,…,ak(1≤k≤2 013,k∈Z)是一個單調遞增數列，則k的最大值是

( )

A.1 005 B.1 006 C.1 007 D.1 008

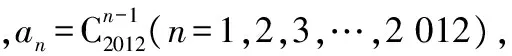
【變式2】二項式(1-x)10的展開式中二項式系數最大的項是第________項.

【答案】6 【解析】展開式共11項，中間項為第6項，二項式系數最大.

【變式3】若(x-2y)n展開式中二項式系數最大的是第5項，則展開式中所有項的系數和是________.

【答案】1 【解析】因為(x-2y)n展開式中系數最大的是第5項，所以n=8，所以(x-2y)8的展開式中所有項的系數和(-1)8=1.

八、整除問題

【例7】求7777-7被19除所得的余數.

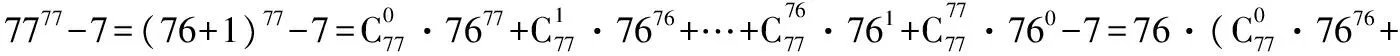
點評：用二項式定理處理整除性問題，通常把底數寫成除數(或與除數密切關聯的數)與某數的和或差的形式，再用二項式定理展開，只考慮后面(或者前面)一、二項就可以了.

【變式1】設a∈Z，且0≤alt;13，若512012+a能被13整除，則實數a= .

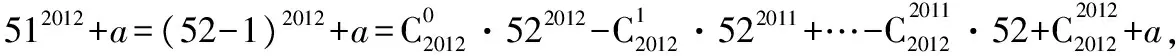
【變式2】已知m是一個給定的正整數，如果兩個整數a，b除以m所得的余數相同，則稱a與b對模m同余，記作a≡b(modm)，例如：5≡13(mod4).若22015≡r(mod7)，則r可能等于

( )

A.2 013 B.2 014 C.2 015 D.2 016

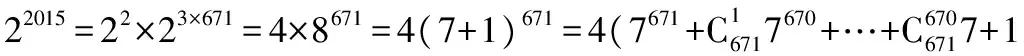
【變式3】用二項式定理證明(n+1)n-1可以被n2整除(n∈N*).

【證明】用二項式定理和組合數的性質，得到

當n=1時，(1+1)1-1能被12整除.

所以(n+1)n-1是n2的倍數，即可以被n2整除.

九、交匯題

( )

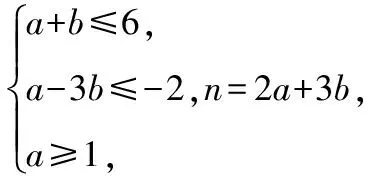
A.-80 B.80 C.40 D.-20

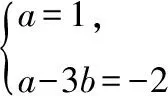
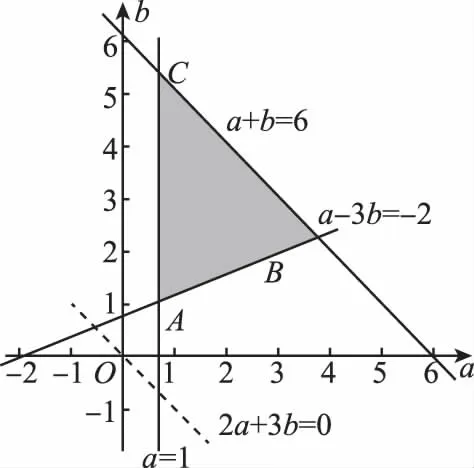
點評：二項式定理常與函數、數列、不等式、導數、復數等知識交匯.求解本題的關鍵是利用線性規劃的知識求出滿足條件的n，再利用二項式定理的知識求解.

( )

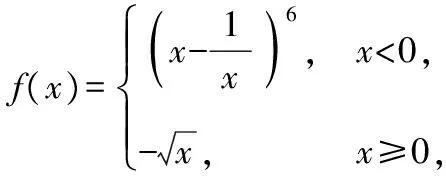
A.-20 B.20 C.-15 D.15

( )

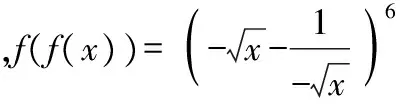
A.240 B.-240 C.-60 D.60

( )

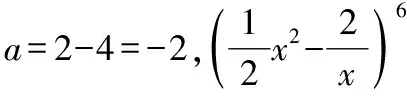
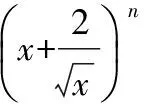
A.第7項 B.第8項

C.第9項 D.第10項

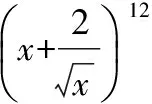
湖北省巴東縣第三高級中學)