從課本習題到高考試題

江蘇 周永興

從課本習題到高考試題

江蘇 周永興

一、提出問題

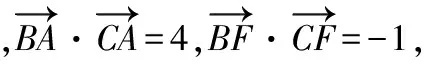
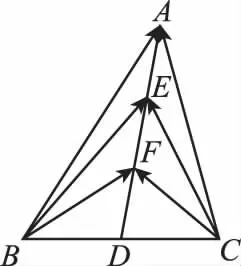
二、理論依據及兩個變形

問題2：(蘇教版必修四教材89頁12題)求證：|a+b|2+|a-b|2=2(|a|2+|b|2)，如何構造一個圖形解釋這個公式的幾何意義？

證明：只研究a,b不共線的情形.

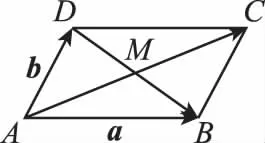
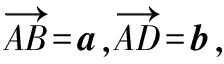
這表明，平行四邊形對角線的平方和等于相鄰兩邊平方和的兩倍.

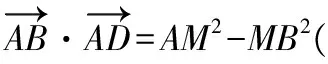
向量是連接代數和幾何的橋梁，極化恒等式源于教材又高于教材，它最初出現在高等數學中的泛函分析，它的巧妙之處在于建立了向量和幾何長度(數量)之間的橋梁，實現了向量與幾何、代數的有機結合，在解決與數量積有關的問題,特別是共起點的向量數量積的最值問題中有著獨特的作用，也越來越受到各種命題老師的青睞.

三、問題1的解決

解法1：引進一組基底，轉化為基向量的運算

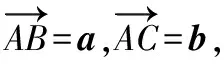
解法2：特殊化，坐標法思想

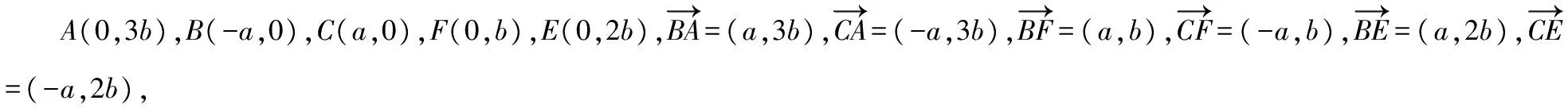
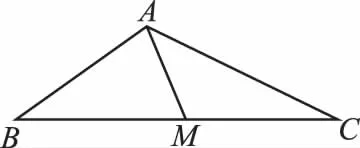
解法3：用極化恒等式，將向量問題幾何化

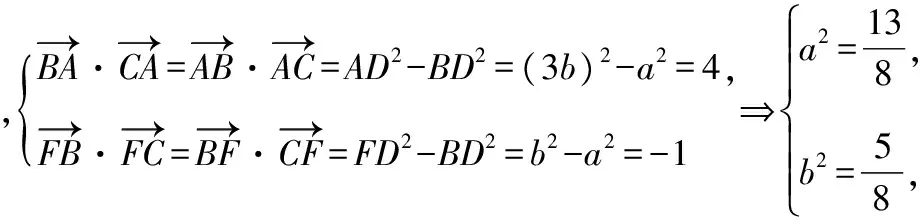
四、教材相關題再現

問題3：(蘇教版必修四教材98頁20題)設a,b,c都是單位向量，且a·b=0，求(c-a)·(c-b)的最小值.

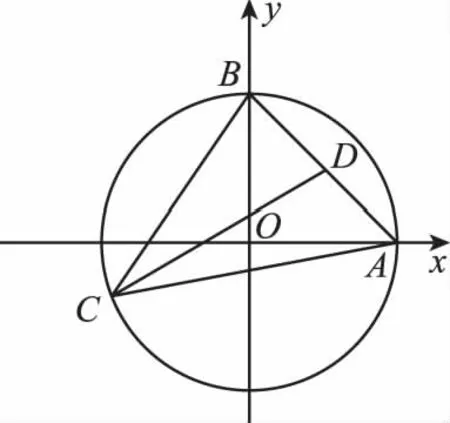
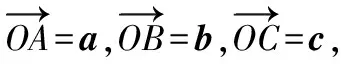
五、近五年各地高考題鏈接

其實,“極化恒等式”在高考數學試卷中的出現早就不是第一次了,請看以下幾個高考題：

( )

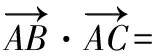
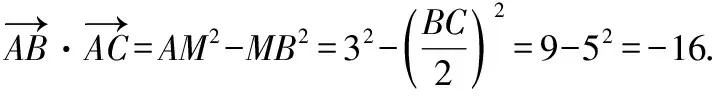
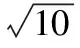
A.1 B.2

C.3 D.5

( )

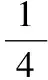
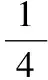
A.∠ABC=90° B.∠BAC=90°

C.AB=ACD.AC=BC

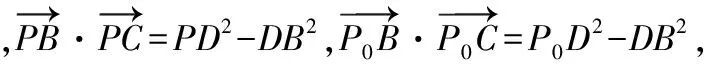
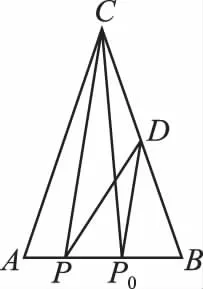
江蘇省前黃高級中學)