2017年高考“數學文化類”試題賞析
山東 尹承利
2017年高考“數學文化類”試題賞析
山東 尹承利
2017年高考在萬眾矚目下落下了帷幕,在高考試題中滲透數學文化成為今年數學高考的一大亮點,全國的一、二卷和高考改革地區的浙江卷都做了有益的嘗試和探索,體現了高考“增加數學文化”的要求.先睹為快,筆者就2017年高考中的數學文化類試題特點予以梳理并賞析,與諸位同仁分享.
一、以古代數學名題為題源
【例1】(2017·全國卷Ⅱ理3)我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈
( )
A.1盞 B.3盞
C.5盞 D.9盞
【解析】可設最頂層燈塔所掛燈數為a,則第二層為2a,第三層為4a,……,第七層為64a,所以本題實質是考查等比數列求和公式,故127a=381,可得a=3,故選B.
【點評】我國古代數學有著極其輝煌的成就,出現過像劉徽、祖沖之、秦九韶、楊輝等偉大的數學家,以及《九章算術》、《數書九章》、《算數書》、祖暅原理等數學名著、名題,以這些名著、名題為試題背景,可以引導我們理解數學,感受數學家的崇高品質以及探究、解決數學問題的過程,進而體會中國古代數學的偉大貢獻,增強愛國主義情懷.程大位是我國明代偉大的數學家,被譽為“珠算之父”,他的應用數學巨著《算法統宗》的問世,標志著我國的算法由籌算到珠算轉變的完成.程大位在《算法統宗》中常以詩歌的形式呈現數學問題,體現了數學的“文化美”.
尤其指出是:2017年《教學考試》數學第1期題組變式訓練(二)《數列與推理》第4題押中了該高考題,說明了《教學考試》(數學)在研究高考命題規律方面具備很深的造詣.
【變式1】我國古代數學名著《算法統宗》中有一首叫“寶塔裝燈”的詩,內容為“遠望巍巍塔七層,紅燈點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”(“倍加增”指燈的數量從塔的頂層到底層按公比為2的等比數列遞增),根據此詩,可以得出塔的頂層和底層共有
( )
A.3盞燈 B.192盞燈
C.195盞燈 D.200盞燈

【變式2】我國古代數學名著《算法統宗》中有一道“竹筒容米”問題:“家有九節竹一莖,為因盛米不均平,下頭三節三升九,上梢四節貯三升,唯有中間二節竹,要將米數次第盛,若有先生能算法,也教算得到天明.”([注釋]三升九:3.9升.次第盛:盛米容積依次相差同一數量.)用你所學的數學知識求得中間兩節的容積為
( )
A.1.9升 B.2.1升
C.2.2升 D.2.3升
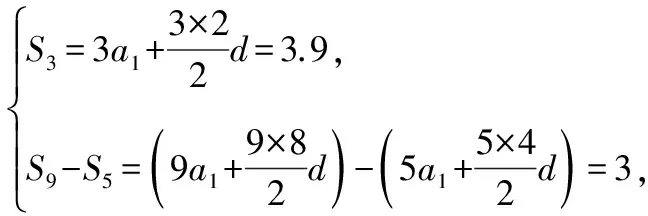
二、以古代著名方法為背景命題
【例2】(2017·浙江11)我國古代數學家劉徽創立的“割圓術”可以估算圓周率π,理論上能把π的值計算到任意精度.祖沖之繼承并發展了“割圓術”,將π的值精確到小數點后七位,其結果領先世界一千多年.“割圓術”的第一步是計算單位圓內接正六邊形的面積S6,S6=________.

【點評】說到圓周率π,自然想到我們引以為豪的“徽率”和“祖率”,它的歷史饒有趣味.我國古代數學家對圓周率方面的研究工作,成績十分地突出.本題所介紹的祖沖之研究圓周率π的成果,使我們感到無比的自豪和驕傲.古代科學家在艱難的環境中研究科學的精神和崇高品質,是值得我們尊敬和學習的.
【變式3】割圓術是我國古代數學家劉徽創造的一種求周長和面積的方法:隨著圓內接正多邊形邊數的增加,它的周長和面積越來越接近圓周長和圓面積,“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣”.試用這個方法解決問題:如圖,⊙O的內接多邊形周長為3,⊙O的外切多邊形周長為3.9,則下列各數中與此圓的周長最接近的是
( )
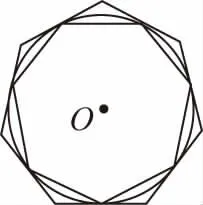
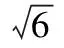
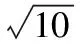
【解析】圓外切多邊形的周長大于圓周長,圓內接多邊形的周長小于圓周長.圓的內接多邊形周長為3,外切多邊形周長為3.9,所以圓周長在3與3.9之間.只有C選項滿足條件.故選C.
三、以古代經典圖形為背景命題
【例3】(2017·全國卷Ⅰ文4、理2)如圖,正方形ABCD內的圖形來自中國古代的太極圖.正方形內切圓中的黑色部分和白色部分關于正方形的中心成中心對稱.在正方形內隨機取一點,則此點取自黑色部分的概率是
( )

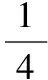


【點評】我國傳統文化中很多內容體現了數學的“對稱美”.如圖所示的太極圖是由黑白兩個魚形紋組成的圓形圖案,充分體現了相互轉化、對稱統一的形式美、和諧美.
【變式4】大衍數列來源于《乾坤譜》中對易傳“大衍之數五十”的推論.主要用于解釋中國傳統文化中的太極衍生原理.數列中的每一項,都代表太極衍生過程中,曾經經歷過的兩儀數量總和.是中華傳統文化中隱藏著的世界數學史上第一道數列題.其前10項依次是0,2,4,8,12,18,24,32,40,50,…,則此數列第20項為
( )
A.180 B.200
C.128 D.162
【答案】B
【變式5】給出定義:能夠將圓O的周長和面積同時平分的函數稱為這個圓的“優美函數”.給出下列命題:
①對于任意一個圓O,其“優美函數”有無數個;

③正弦函數y=sinx可以同時是無數個圓的“優美函數”;
④函數y=f(x)是“優美函數”的充要條件為函數y=f(x)的圖象是中心對稱圖形.
其中正確的有
( )
A.①③ B.①③④
C.②③ D.①④
【答案】A
四、推理論證常考常新
【例4】(2017·全國卷Ⅱ文9、理7)甲、乙、丙、丁四位同學一起去向老師詢問成語競賽的成績,老師說:你們四人中有2位優秀,2位良好,我現在給甲看乙、丙的成績,給乙看丙的成績,給丁看甲的成績.看后甲對大家說:我還是不知道我的成績,根據以上信息,則
( )
A.乙可以知道四人的成績
B.丁可以知道四人的成績
C.乙、丁可以知道對方的成績
D.乙、丁可以知道自己的成績
【解析】由甲說不知道自己成績且看過乙和丙的成績,可推出乙和丙一優一良,又因為乙看過丙的成績,所以乙可以推測出自己的成績,因為已經推出乙和丙一優一良,所以甲和丁也是一優一良,并且條件已給出丁看過甲的成績,所以丁也可以推測出自己成績,故選D.
【點評】推理論證問題是近幾年高考中常考常新的重要題型,2014年高考全國卷Ⅰ文、理14題曾做過考查,今年卷Ⅱ又再一次考查到.以邏輯推理問題命制高考題,既能創造寬松又競爭的環境,拉近考生與數學的心理距離,又能考查學生的閱讀理解能力和邏輯推理能力.乍看這類問題,高中所學的知識好像在此全無用武之地,練就百遍的解題技巧似乎也在此擱淺,然而數學思維能力,卻在此大放光彩.
【變式6】在一個俱樂部里,有老實人和騙子兩類成員,老實人永遠說真話,騙子永遠說假話.一次我們和俱樂部的四個成員談天,我們便問他們:“你們是什么人,是老實人?還是騙子?”這四個人的回答如下:
第一個人說:“我們四個人全都是騙子”.
第二個人說:“我們當中只有一個人是騙子”.
第三個人說:“我們四個人中有兩個人是騙子”.
第四個人說:“我是老實人”.
請判斷一下,第四個人是老實人嗎?________.(請用“是”或“否”作答)
【解析】(1)四個人當中一定有老實人,因為如果四個人都是騙子,則誰也不會說“我們四個人全都是騙子”,所以第一個人是騙子.
(2)第二個人為騙子,因為他如果是老實人,由于已經判斷了第一個人是騙子,則第二,三,四個人都是老實人.但第三個人的回答與他矛盾,兩個人不可能是同類的,故第二個人說的是假話,他是騙子.

山東省泰安英雄山中學)

