函數題組訓練
——函數的概念與性質

陜西 劉麥玲

山東 莊艷俠

湖南 歐陽巧林

江蘇 王懷學

函數題組訓練
——函數的概念與性質

陜西 劉麥玲

山東 莊艷俠

湖南 歐陽巧林

江蘇 王懷學

1.函數的概念

1.1函數是從非空數集A到數集B的單值對應

【典例】高一(9)班1組有6位同學，在某次數學考試的成績如下表所示：

學號123456成績807579809880

根據上表回答問題：

(1)上述問題涉及到幾個變量？

(2)每個變量的取值范圍分別是多少？

(3)學號為4的同學的成績是否唯一確定？成績是80的同學是否唯一？

(4)設變量x是該組同學的學號，變量y是該班同學的成績，則y是x的函數嗎？

【解析】(1)上述問題涉及兩個變量，即學號與成績；

(2)學號的取值范圍是{1，2，3，4，5，6}；成績的取值范圍是{75，79，80，98}；

(3)學號為4的同學的成績是80，是確定的唯一的；成績是80的對應3位同學；

(4)y是x的函數.

【評注】兩個變量x，y都有自己的取值范圍，對于x每取一個值，相當于在集合A中任取一個數；變量y都有且僅有唯一的值和它對應，相當于在集合B中有且僅有唯一的元素和它對應.

本題中，若設變量x是該組同學的學號，變量y是該班同學的姓名，顯然y也不是x的函數.

【變式1】下列對應關系是從A到B的函數的有________．

(1)A={1，2，3，4，5}，B={0，2，4，6，8}，x→2x，x∈R；

(2)A={x|x是矩形}，B={x|x為圓}，f:每個矩形的外接圓；

(3)A={1，2，3，4}，B={x|xlt;10，x∈N}，x→2x+1，x∈R；

(4)A=B=N*，x→x-1，x∈A.

【變式2】在下列對應關系中，f(x)滿足函數關系的是

( )

A.f(sin2x)=sinx

B.f(sin2x)=x2+x

C.f(x2+1)=|x+1|

D.f(x2+2x)=|x+1|

1.2圖象一樣的函數就是同一函數

【典例】下列函數中一定是同一函數的是

( )

A.①④ B.②③

C.①③ D.②④

【解析】①中，兩個函數的定義域不同；

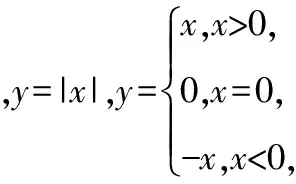
對于④，兩個函數的對應關系不相同，定義域也不同．

故選B.

【變式1】下列各組函數表示同一函數的是

( )

A.f(x)=sinx，g(x)=cosx

B．f(x)=2sinx，g(x)=2cosx

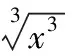
【變式2】下列各組函數表示同一函數的是

( )

A.f(x)=sinx，g(x)=tanx

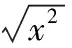
C．f(x)=x，g(x)=x+1

D．f(x)=sin2x+cos2x，x∈R與g(x)=1，x∈R

2函數的定義域

2.1簡單的不等式(組)的求法

【典例】解下列不等式組：

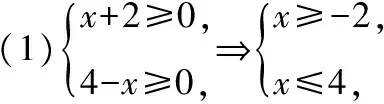
所以{x|-2≤x≤4}；

所以x2=1，x=±1，不等式解集是{-1，1}；

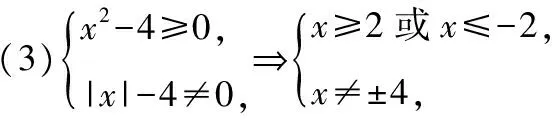
于是{x|x≤-2且x≠-4或x≥2且x≠4}；

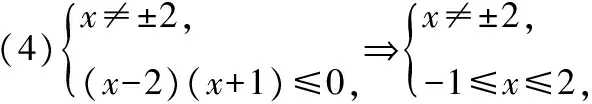
由數軸可知，不等式組的解集是{x|-1≤xlt;2}.

【變式1】求下列函數的定義域.

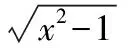
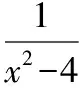
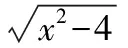
2.2使解析式有意義的自變量取值集合是函數的定義域

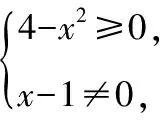
所以函數f(x)的定義域是[-2,1)∪(1,2].

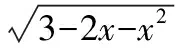
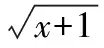
2.3復合函數的定義域也是自變量x的取值范圍

( )

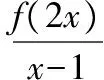
A.[0,1] B.[0,1)

C.[0,1)∪(1,4] D.(0,1)

【解析】因為f(x)的定義域為[0，2]，

所以對g(x),0≤2x≤2,且x≠1,

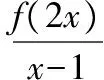
【變式1】已知函數f(x)的定義域為(-1,0)，則函數f(2x+1)的定義域為

( )

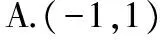
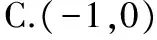
【變式2】已知f(x)的定義域為[-2,3]，則函數f(x-2) 的定義域是________.

2.4求函數解析式遇到的函數定義域問題

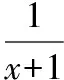
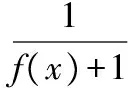
【變式1】已知f(x2+1)=2x2+3，則f(x)=________．

2.5用區間或集合表示函數定義域

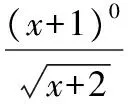
2.6對數函數定義域不能成為永遠的痛

【典例1】求下列函數的定義域：

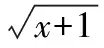
(2)y=log7(x2-2x-3)；

(3)y=log(x+1)(16-4x)；

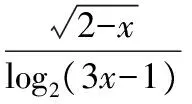
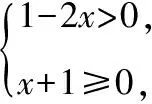
(2)因為x2-2x-3gt;0，即(x-3)(x+1)gt;0，解得xlt;-1或xgt;3，即函數的定義域是(-∞，-1)∪(3，+∞)；

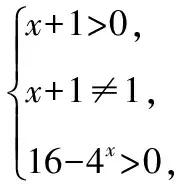
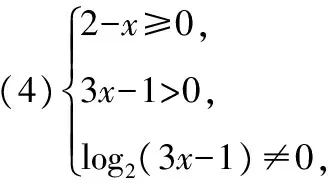
【變式1】求下列函數的定義域：

(1)y=log(x-1)(3-x)；

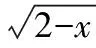
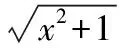
【典例2】已知函數f(x)=logax(agt;0，a≠1)在其定義域內為增函數，則滿足f(|x-1|)lt;0的實數x的取值范圍為________．

【解析】f(|x-1|)lt;0等價于loga|x-1|lt;loga1，

則0lt;|x-1|lt;1，

即-1lt;x-1lt;1且x≠1?0lt;xlt;2且x≠1，

所以實數x的取值范圍(0，1)∪(1，2)．

【變式1】“Mgt;N”是“log2Mgt;log2N”成立的________條件(用“充要”“充分不必要”“必要不充分”“既不充分也不必要”填空)

【變式2】已知定義在集合A上的函數f(x)=log2(x-1)+log2(2x+1)，其值域為(-∞，1]，則A=________．

3.函數的值域

3.1先內后外求復合函數的函數值

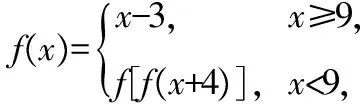
【解析】因為7lt;9，

所以f(7)=f[f(7+4)]=f[f(11)].

因為11gt;9，所以f(11)=11-3=8，

所以f(7)=f(8)；

因為8lt;9，所以f(8)=f[f(8+4)]=f[f(12)]，

所以f(7)=f(8)=f[f(12)]；

因為12gt;9，所以f(12)=12-3=9，

所以f(7)=f(8)=f(9)；

因為9=9，所以f(9)=9-3=6，

所以f(7)=f(8)=f(9)=6；

所以f(7)=6.

( )

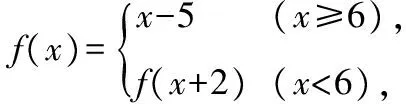
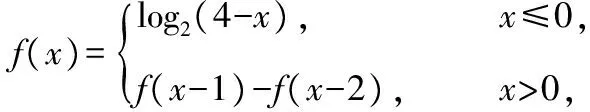
A.-1 B.-2

C.1 D.2

( )

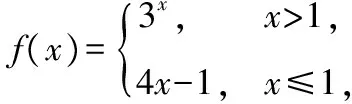
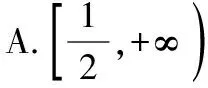
C.(1,+∞) D.[1,+∞)

3.2賦值法求函數的值

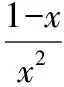
【解析】令g(x)=-3，1-2x=-3，x=2，g(2)=-3.

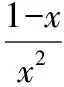
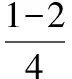
【變式1】已知f(x+2)=2x+3，則f(8)=________.

【變式2】已知f(x+1)=3(x-2 017)2+1，則f(2 018)=________.

3.3分離常數法求函數值域

【典例】求下列函數的值域：

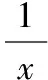
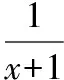
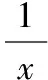
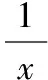
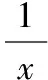
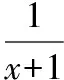
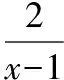
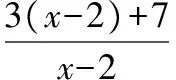
3.4基本不等式法求函數值域

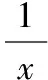
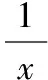
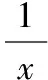
即y≤-1或y≥3.

所以所求函數的值域為(-∞,-1]∪[3,+∞).

( )

A．-3 B．3

C．4 D．-4

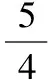
3.5三角換元法求函數值域

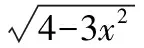
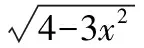
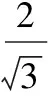
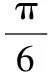
3.6函數單調性法求最值(值域)

【解析】此函數的定義域為[1,+∞)，且是增函數，當x=1時，ymin=1，函數的值域為[1,+∞).

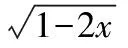
3.7有界性法求函數的值域

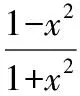
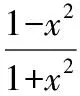
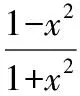
所以-1lt;y≤1，即函數值域為(-1，1]．

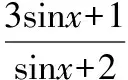
3.8不等式性質或函數圖象求值域

【典例1】求下列函數的值域：

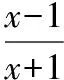
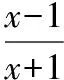
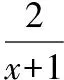
所以f(x)≠1，所以函數值域是(-∞，1)∪(1，+∞)；

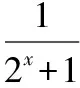
所以函數值域是{y|1lt;ylt;2}；

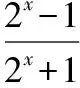
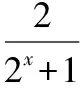
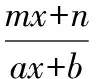
【變式1】函數f(x)=x2-2x+3的值域是________.

【變式2】函數f(x)=2-3-x(-1≤x≤2)的值域是________.

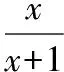
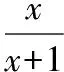
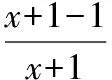
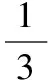
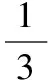
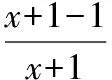
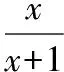
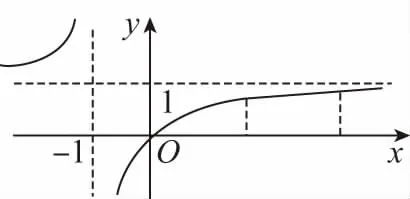
函數f(x)在[2，4]上單調遞增，

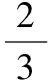
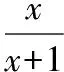
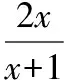
(1)求證：函數f(x)在(0,+∞)上是單調增函數；

(2)已知g(x)=log2f(x)，求函數g(x)=log2f(x)的值域.

4.函數的解析式

4.1已知函數的名稱用待定系數法求解析式

【典例】求一個實系數的一次函數f(x)，使得f{f[f(x)]}=8x+7.

【解析】設f(x)=ax+b(a≠0)，

則f{f[f(x)]}=a[a(ax+b)+b]+b

=a3x+a2b+ab+b

=8x+7,

所以a3=8且a2b+ab+b=7,解得a=2,b=1.

故所求f(x)=2x+1.

【變式1】若一次函數f(x)滿足f[f(x)]=4x-3，則函數f(x)的解析式為________.

【變式2】已知函數f(x)=2x+3，g(x)=4x-5，求滿足f[h(x)]=g(x)的h(x)為________.

4.2構造方程組用消去法求函數解析式

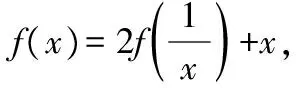
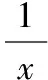
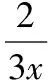
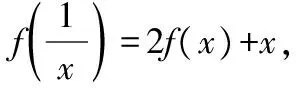
【變式2】已知函數f(x)滿足f(1-x)=2f(x)-x2，求函數f(x)的解析式.

【典例2】已知f(x)，g(x)分別是定義在R上的偶函數和奇函數，且f(x)-g(x)=x3+x2+1，求f(x),g(x).

【解析】由已知得f(-x)-g(-x)=-x3+x2+1，

即f(x)+g(x)=-x3+x2+1，與f(x)-g(x)=x3+x2+1聯立解方程組，得f(x)=x2+1，g(x)=-x3．

【變式1】若函數f(x)，g(x)分別是R上的奇函數、偶函數，且滿足f(x)-g(x)=ex，則g(0),f(2),f(3)的大小關系是________.

4.3用換元法(配湊法)求函數f(x)的解析式

【典例1】求分別滿足下列條件的函數f(x)的解析式：

(1)f(x-1)=(x-1)2+1；

(2)f(x-1)=x2-2x+2；

(3)f(x-1)=3x-2；

(4)f(2x)=3x2+1.

【解析】(1)f(x)=x2+1；

(2)因為f(x-1)=(x-1)2+1，所以f(x)=x2+1；

(3)因為f(x-1)=3(x-1)+1，所以f(x)=3x+1；

【變式1】已知f(x+1)=x2-2x+2，則f(x+3)=________.

4.4根據兩函數圖象的關系進行坐標轉移法

( )

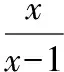
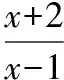
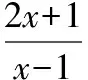
【解析】設函數g(x)的圖象上任意一點(x,y)，

因為點(x,y)關于直線y=x的對稱點為(y,x)，

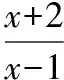
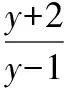
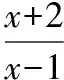
【變式1】已知函數f(x)=x2+2x-3，當點(x，y)在y=g(x)的圖象上運動時，點(2x，3y)在函數y=f(x)圖象上運動，則y=g(x)的解析式是____________.

【變式2】已知函數y=ex的圖象與函數y=f(x)的圖象關于直線y=x對稱，則

( )

A．f(2x)=e2x(x∈R)

B．f(2x)=ln2·lnx(xgt;0)

C．f(2x)=2ex(x∈R)

D．f(2x)=lnx+ln2(xgt;0)

4.5判別式法求最值

【典例1】已知關于x的方程tx2+4x+t+3=0有實數解，求實數t的取值范圍．

【解析】當t=0,4x+3=0有實數解；

當t≠0，關于x的方程tx2+4x+t+3=0有實數解等價于二次函數f(x)=tx2+4x+t+3在R上必與x軸有交點，則Δ=16-4t(t+3)≥0,得t2+3t-4≤0，所以-4≤t≤1且t≠0．

綜上，實數t的取值范圍{t|-4≤t≤1}．

【變式1】已知關于x的一元二次方程kx2+2x-3=0有實數解，求實數k的取值范圍.

【變式2】關于x的方程(y+1)x2-6x-y+9=0在(0,1)上有解，求正數y的取值范圍.

【典例2】設x,y為實數，若4x2+y2+xy=1,則2x+y的最大值是________.

【解析】設2x+y=t，則y=t-2x，

代入4x2+y2+xy=1整理得6x2-3tx+t2-1=0，

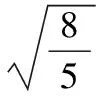
【變式1】若x,y∈R，設M=x2-2xy+3y2-x+y，則M的最小值為________.

【變式2】設x,y為實數，若x2-3xy+y2=2，則x2+y2的最小值是________.

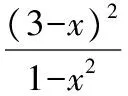
【解析】(y+1)x2-6x+9-y=0在(0，1)上有解，

也就是二次函數f(x)=(y+1)x2-6x+9-y(ygt;0)在(0，1)上與x軸有公共點.

故函數的最小值為8.

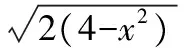
【變式2】若正數x,y滿足x+3y=5xy，則3x+4y的取值范圍是________.

5.函數性質

5.1函數的單調性

( )

A．f(-5)gt;f(3)

B．f(-5)lt;f(3)

C．f(-3)gt;f(-5)

D．f(-3)lt;f(-5)

【解析】f(x)在(0，+∞)上為增函數，又為奇函數，故f(x)在(-∞，0)上也為增函數，因為-3gt;-5，所以f(-3)gt;f(-5)，故選C.

( )

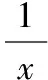
B．f(x)=(x-1)2

C．f(x)=ex

D．f(x)=ln(x+1)

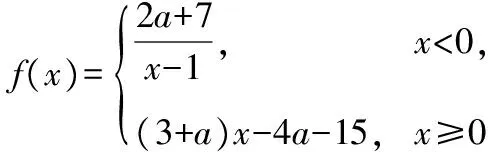
【典例2】已知函數y=f(x)的定義域是(0，2)，且對于任意的正數m，都有f(x+m)lt;f(x)，求滿足f(2-a)lt;f(a2)的實數a的取值范圍.

【解析】因為對于任意的正數m，都有f(x+m)lt;f(x)，所以函數y=f(x)在(0，2)上單調遞減.

因為函數y=f(x)在(0，2)上單調遞減，

且f(2-a)lt;f(a2)，所以2-agt;a2，

又函數定義域是(0，2)，

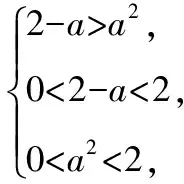
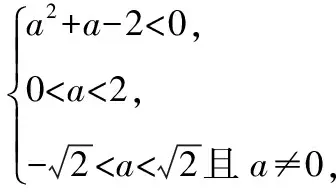
因此實數a的取值范圍是0lt;alt;1.

【變式1】已知函數y=f(x)在定義域R上是單調增函數，且f(x2+x)gt;f(2)，求實數x的取值范圍.

【變式2】已知函數y=f(x)在[0，2]上是單調增函數，且f(x+1)gt;f(2x)，求實數x的取值范圍.

【典例3】(1)函數f(x)在(-∞，+∞)上單調遞減，且為奇函數．若f(1)=-1，則滿足-1≤f(x-2)≤1的x的取值范圍是

( )

A．[-2，2] B．[-1，1]

C．[0，4] D．[1，3]

(2)設函數y=f(x)為R上的單調增函數，函數圖象經過(3，1)，求不等式f(x)≤1的解集.

【解析】(1)因為函數為奇函數且f(1)=-1，

要滿足-1≤f(x-1)≤1，

即f(-1)≤f(x-1)≤f(1)，

又函數在R上單調遞減，所以-1≤x-1≤1，

得1≤x≤3，所以x∈[1，3]，故選D.

(2)函數圖象經過(3，1)，則f(3)=1，

所以f(x)≤f(3)，

因為函數y=f(x)為R上的單調增函數，所以x≤3，

不等式f(x)≤1的解集是{x|x≤3}.

【典例4】已知函數f(x)=x3+x對任意的m∈[-2，2]，有不等式f(mx-2)+f(x)lt;0恒成立，求實數x的取值范圍.

【解析】因為f′(x)=3x2+1gt;0，

所以f(x)=x3+x在R上單調遞增，

又f(x)=x3+x為奇函數，

因此不等式f(mx-2)+f(x)lt;0等價于mx-2lt;-x，

即(m+1)xlt;2對任意的m∈[-2，2]恒成立.

(法1)當m=-1時，x∈R；

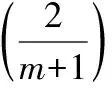
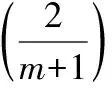
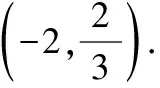
(法2)設g(m)=xm+x,

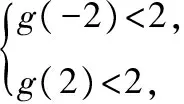
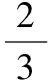
【變式1】已知函數f(x)=2x+sinx對任意的m∈[-2，2]，有不等式f(mx-3)+f(x)lt;0恒成立，則x的取值范圍是________.

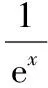
5.2函數的奇偶性

【典例1】已知函數f(x)=asin3x+bx3+4(a∈R,b∈R)，f′(x)為f(x)的導函數，則f(2 014)+f(-2 014)+f′(2 015)-f′(-2 015)=

( )

A．8 B．2 014

C．2 015 D．0

【解析】f(x)=asin3x+bx3+4(a∈R，b∈R)，

f(-x)=-asin3x-bx3+4，

所以f(2 014)+f(-2 014)=8.

又因為f′(x)=3acos3x+3bx2為偶函數，

所以f′(2 015)-f′(-2 015)=0，

f(2 014)+f(-2 014)+f′(2 015)-f′(-2 015)=8.

故選A.

【變式1】函數f(x)=x3+sinx+1(x∈R)，若f(a)=2，則f(-a)的值為

( )

A.3 B.0

C.-1 D.-2

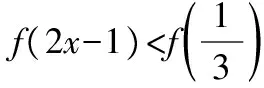
【解析】(法1)由于f(x)是偶函數，故f(|x|)=f(x)，

【變式1】定義在R上的偶函數g(x)，當x≥0時g(x)單調遞減，若g(1-m)lt;g(m)，則m的取值范圍是________．

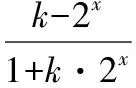
【解析】由f(x)是奇函數，所以f(x)+f(-x)=0，

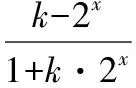
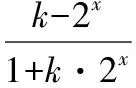
所以k2=1,k=±1．經檢驗符合.

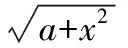
5.3函數圖象的對稱性

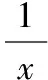
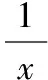
定義域為{x|x≠0且x≠-1}，

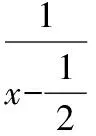
該函數為奇函數關于原點中心對稱，

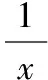
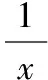
故原來的函數對稱中心為(-1,0).

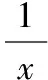
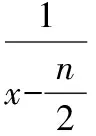
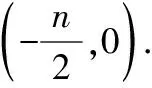
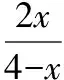
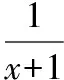
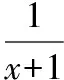
【典例2】函數f(x)=(x-3)3+x-1，數列{an}是公差不為0的等差數列，f(a1)+f(a2)+…+f(a7)=14，求a1+a2+…+a7.

【解析】令g(x)=f(x)-2=(x-3)3+(x-3)，

所以g(x)圖象關于(3，0)對稱．

因為f(a1)+f(a2)+…+f(a7)=14，

所以f(a1)-2+f(a2)-2+…+f(a7)-2=0.

即g(a1)+g(a2)+…+g(a7)=0.

因為g(x)圖象上的點(a1,g(a1)),(a2,g(a2)),(a3,g(a3)),…,(a7,g(a7))與(a7,g(a7)),…,(a3,g(a3)),(a2,g(a2)),(a1,g(a1))關于(a4,g(a4))中心對稱，

即a4=3，故a1+a2+…+a7=7a4=21.

【變式1】將函數g(x)=x3-3x2的圖象向左平移1個單位，再向上平移2個單位，求此時圖象對應的函數解析式，則函數g(x)圖象對稱中心的坐標為________．

【變式2】已知f(x)=(x-1)3+1，則f(-4)+f(-3)+…+f(0)+…+f(5)+f(6)=________.

【變式3】已知函數f(x)=(x+a)3對任意x有f(1+x)=-f(1-x)，則f(-2 015)+f(2 017)的值為________．

5.4函數周期性

(2)設定義在R上的函數f(x)滿足f(x)·f(x+2)=13，若f(1)=2，則f(99)=________.

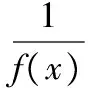
所以f(x)是周期為4的函數，f(5)=f(1)=-5，

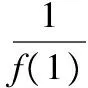
【變式1】設定義在R上的函數f(x)滿足f(x)·f(x+2)=13，若f(1)=2，則f(99)=

( )

A.13 B.2

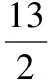
【變式2】設定義在R上的函數f(x)滿足f(x)·f(x+2)=2 016，若f(3)=2，則f(2 017)=________．

( )

A.-2 B.-1

C.0 D.1

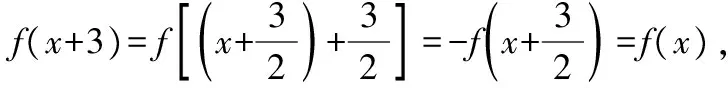
【典例3】已知函數f(x)的定義域為R，f(x+1)=-f(x-2)，且f(1)=1，則f(64)=________．

【解析】f(x+1)=-f(x-2),用x+2替換x,

得f(x+3)=-f(x),f(x+6)=f[(x+3)+3]

=-f(x+3)=-[-f(x)]=f(x),

所以函數f(x)的周期為6.

因為f(1)=1,f(4)=-f(1)=-1,

所以f(64)=f(6×10+4)=f(4)=-1.

【變式1】已知奇函數f(x)圖象關于x=2對稱，且f(1)=1，則f(65)=________.

參考答案

1.函數的概念

1.1函數是從非空數集A到數集B的單值對應

1．(3) 【解析】(1)集合A中的元素5，按照對應法則，在B中應該是對應10，但沒有，不是從A到B的函數；

(2)集合A，B不是數集，不是函數；

(3)f(1)=3，f(2)=5，f(3)=7，f(4)=9，是從A到B的函數；

(4)當x=1時，x-1=0?B，不是從A到B的函數.

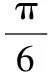
C.f(12+1)=f(2)=2,f((-1)2+1)=f(2)=0,則f(2)=|±1+1|=0,2;

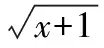
即A，B，C選項均不滿足同一自變量所對應的函數值是唯一的，故選D.

1.2圖象一樣的函數就是同一函數

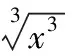
2.D 【解析】A，B，C中函數的圖象不同，D中函數的圖象完全相同，故選D.

2函數的定義域

2.1簡單的不等式(組)的求法

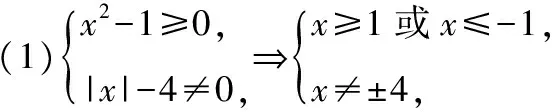
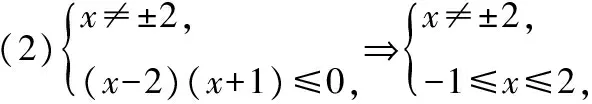
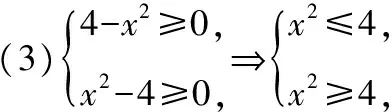
2.2使解析式有意義的自變量取值集合是函數的定義域

1.[-3，1] 【解析】3-2x-x2≥0,解得-3≤x≤1,因此定義域為[-3，1].

2.3復合函數的定義域也是自變量x的取值范圍

2.[0,5] 【解析】由f(x)的定義域為[-2,3]得-2≤x≤3，用x-2替換x得-2≤x-2≤3即0≤x≤5.所以f(x)的定義域為[0,5].

2.4求函數解析式遇到的函數定義域問題

1.f(x)=2x+1(x≥1) 【解析】(配湊法)f(x2+1)=2(x2+1)+1，所以f(x)=2x+1(x≥1).

2.6對數函數定義域不能成為永遠的痛

【典例1】

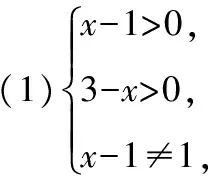
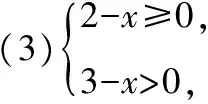
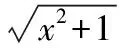
3.【解析】A={x|x-2gt;0}=(2，+∞)，B={x|x-1≥0}=[1，+∞).A∪B=(2,+∞)∪[1，+∞)=[1，+∞)，A∩B=(2，+∞)∩[1，+∞)=(2，+∞).

【典例2】

1.必要不充分 【解析】由Mgt;N，不能得到log2Mgt;log2N，因為M，N不一定大于0.反過來，由log2Mgt;log2N可得Mgt;N.

3.1先內后外求復合函數函數的值

1.3 【解析】f(3)+f(6)=f(5)+1=f(7)+1=2+1=3.

2.B 【解析】由題f(x)=f(x-1)-f(x-2)，xgt;0，得f(3)=f(2)-f(1)=f(1)-f(0)-f(1)=-f(0)，f(0)=log2(4-0)=2，則-f(0)=-2，故選B.

3.2賦值法求函數的值

1.15 【解析】由8=x+2，x=6，由f(x+2)=2x+3得f(6+2)=2×6+3=15.

2.1 【解析】令x=2 017，f(x+1)=f(2 017+1)=f(2 018)，所以f(2 018)=f(2 017+1)=3(2 017-2 017)2+1=1.

3.4基本不等式法求函數值域

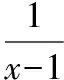
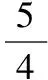
3.5三角換元法求函數值域

3.6函數單調性法求最值(值域)

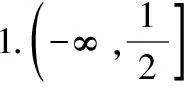
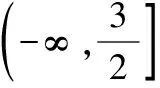
3.7有界性法求函數的值域

3.8不等式性質或函數圖象求值域

【典例1】

1.[2，+∞) 【解析】f(x)=(x-1)2+2≥2，所以函數f(x)=x2-2x+3的值域是[2，+∞).

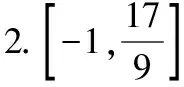
【典例2】

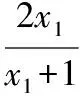
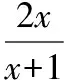
(法2)因為xgt;0,所以x+1gt;1，

可以得到函數f(x)的值域(0，2)，

所以g(x)=log2f(x)的值域是(-∞，1).

4.1已知函數的名稱用待定系數法求解析式

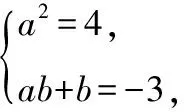
2..h(x)=2x-4 【解析】因為f(x)和g(x)均為一次函數，所以h(x)為一次函數，設h(x)=ax+b，所以f[h(x)]=2h(x)+3=2(ax+b)+3=2ax+2b+3=4x-5，所以2a=4，2b+3=-5，解得a=2，b=-4，所以h(x)=ax+b=2x-4.

4.2構造方程組用消去法求函數解析式

【典例1】

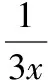
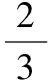
【典例2】

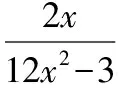
4.3用換元法(配湊法)求函數f(x)的解析式

1.f(x+3)=x2+2x+2 【解析】設t=x+1，x=t-1，則f(t)=(t-1)2-2(t-1)+2=t2-4t+5，所以f(x)=x2-4x+5，f(x+3)=(x+3)2-4(x+3)+5=x2+2x+2.

4.4根據兩函數圖象的關系進行坐標轉移法

2.D 【解析】設函數y=f(x)的圖象上任意一點(x，y)，則因為點(x，y)關于直線y=x的對稱點為(y，x)，所以(y，x)滿足方程y=ex，即x=ey，兩邊取對數得，lnx=y，即f(x)=lnx，故f(2x)=ln2x=lnx+ln2(xgt;0)，故選D.

4.5判別式法求最值

【典例1】

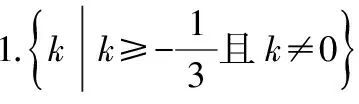
【典例2】

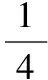
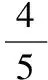
【典例3】

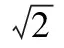
5.函數性質

5.1函數的單調性

【典例1】

【典例2】

1.xgt;1或xlt;-2 【解析】由題意得x2+xgt;2，(x-1)(x+2)gt;0，得xgt;1或xlt;-2，實數x的取值范圍xgt;1或xlt;-2.

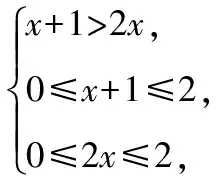
【典例4】

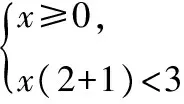
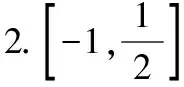
5.2函數的奇偶性

【典例1】

1.B 【解析】f(a)=a3+sina+1，f(-a)=-a3-sina+1，f(a)+f(-a)=2，故f(-a)=0,故選B.

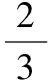
【典例2】

【典例3】

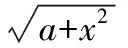
5.3函數圖象的對稱性

【典例1】

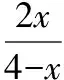
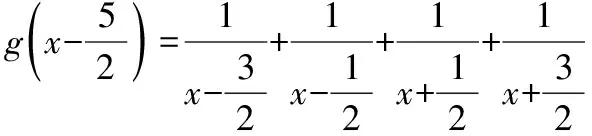
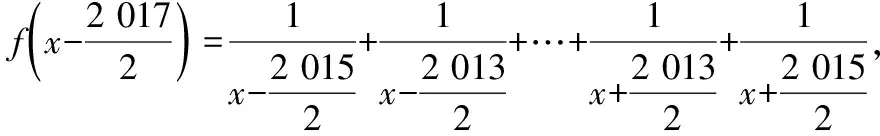
【典例2】

1.(1，-2) 【解析】平移后得g1(x)=(x+1)3-3(x+1)2+2，即g1(x)=x3-3x．由函數y=g1(x)為奇函數，它的對稱中心為O(0，0)，所以函數g(x)=x3-3x2的對稱中心為(1，-2)．

2.11 【解析】f(x)=(x-1)3+1是由y=x3平移得到的，因此f(x)的對稱中心為(1，1)，有f(x)+f(2-x)=2，所以f(-4)+f(-3)+…+f(0)+…+f(5)+f(6)=[f(-4)+f(6)]+[f(-3)+f(5)]+…+[f(0)+f(2)]+f(1)=5×2+1=11．

3.0 【解析】用1-x替換x得f(2-x)=-f(x)，即f(2-x)+f(x)=0，可知函數f(x)關于點(1，0)對稱，所以f(-2 015)+f(2 017)=0.

5.4函數周期性

【典例1】

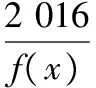
【典例3】