巧用投影模型，速解一類數量積問題

江蘇 魏美云

巧用投影模型，速解一類數量積問題

江蘇 魏美云

平面向量知識在高中教材中占有重要地位，有關內容已經成為高考的重點和熱點，特別是平面向量的數量積更是高考的必考內容．近年來有關數量積的試題具有一定的綜合性，思維量大，解法也越來越靈活．解決數量積問題的常用方法有定義法、基向量法、坐標法等，而數量積的幾何意義卻常被遺忘．實際上，巧用幾何意義能快速解決一類數量積問題．下面從數量積的定義入手，介紹與幾何意義有關的三個結論及其應用，幫助學生豐富視野、開拓思路．

平面向量數量積的定義：已知兩個非零向量a和b，我們把數量|a||b|cosθ叫做a與b的數量積(或內積)，記作a·b，即a·b=|a||b|cosθ，其中θ是a與b的夾角．|a|cosθ叫做向量a在b方向上的投影，|b|cosθ叫做向量b在a方向上的投影．

平面向量數量積a·b的幾何意義：數量積a·b等于a的長度|a|與向量b在a方向上的投影|b|cosθ的乘積(或者等于b的長度|b|與向量a在b方向上的投影|a|cosθ的乘積)．

根據平面向量數量積的定義和幾何意義，容易得到以下三個結論，下面介紹三個結論及其應用．

結論一：如果向量a，b在向量c方向上的投影相等，則a·c=b·c.

【證明】根據數量積的定義得

a·c=|a||c|cosα，b·c=|b||c|cosβ，其中α是a與c的夾角，β是b與c的夾角．

因為向量a，b在向量c方向上的投影相等，得|a|cosα=|b|cosβ，所以a·c=b·c．

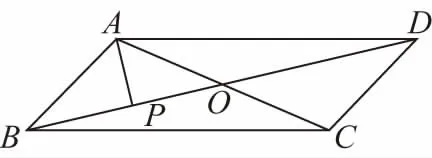
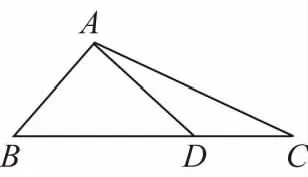
【解析】如圖，設邊BC的中點為O，則PO⊥BC，

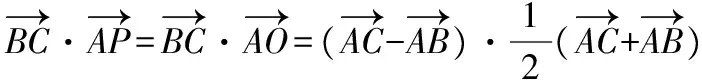
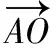
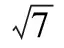
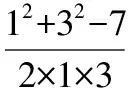
過O作OD⊥AC交AC于點D，

因為O是△ABC的垂心，

所以O，B，D三點共線，

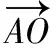
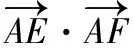
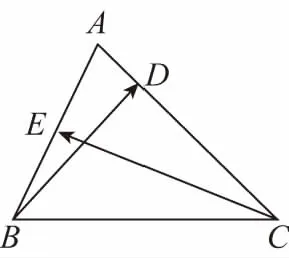
【解析】如圖，過點F作FG⊥AE于點G，

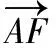
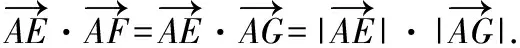
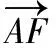
【提示】過點F作FG⊥AB于G，

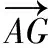
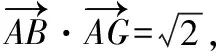
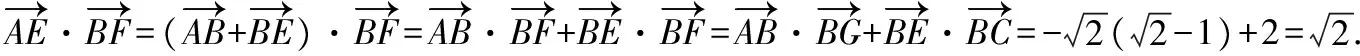
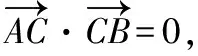
利用結論一也能快速證明．

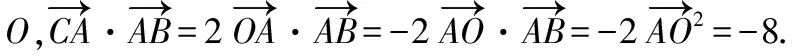
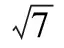
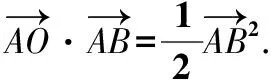
【證明】如圖，取弦AB的中點M，連接OM，則OM⊥AB，

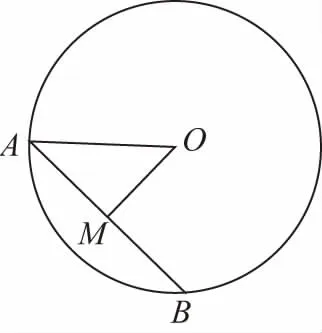
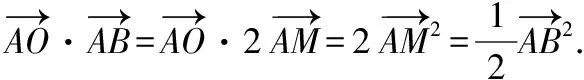
根據這個結論不難得到如下結論：

在△ABC中，O是△ABC的外心，

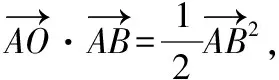
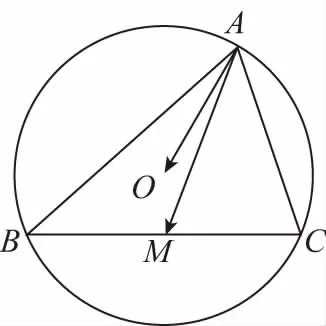
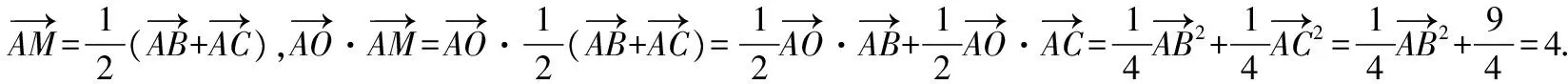
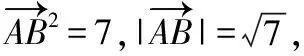
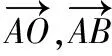
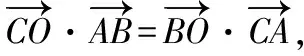
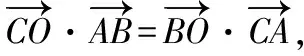
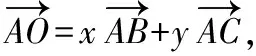
【解析】因為O是△ABC的外心，

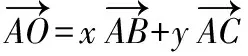
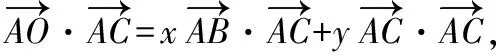
即50=60xcos∠BAC+100y，

即5=6xcos∠BAC+10y，

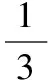
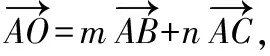
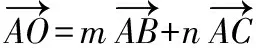
江蘇省沛縣湖西中學)