分類討論還是參變分離?
——淺議不等式恒成立問題的解法

河北 劉立剛

分類討論還是參變分離?
——淺議不等式恒成立問題的解法

河北 劉立剛

函數導數問題中不等式恒成立問題一直倍受命題人的青睞，也一直是學生學習的疑點和高考的熱點.由于其中既含有參數又含有變量，能有效考查學生分析問題、解決問題的能力.

解決此類問題的常見方法一是不等式變形，使不等式一側為具體常數(常常是實數0)，將另一側構造為關于變量x的函數，把不等式恒成立問題轉化成含參數的函數求最值，f(x)gt;0(f(x)lt;0)恒成立?[f(x)]mingt;0([f(x)]maxlt;0)，簡稱“函數法”；二是等價變形將變量x和參數a分別置于不等號兩側，f(x)gt;g(a)恒成立?g(a)lt;[f(x)]min(f(x)lt;g(a)恒成立?g(a)gt;[f(x)]max)，簡稱“參變分離法”.

兩種方法都是轉化為求函數最值，在解決過程中各有利弊：“函數法”通過分類討論將函數求最值分為不同情況，把復雜問題簡單化，但函數中含參數，導致導數符號的不確定性，大部分學生對于帶參數的求導結果的討論會知難而退；而“參變分離法”通過對字母的分離使恒成立問題轉化為不含參數的給定函數的最值，避開了對含參因式的分辨以及主次變量的討論，其弊端是分離后有可能使給定函數形式過于復雜，最值不易求.

同學們在解決此類問題時總有這樣的糾結：到底用“函數法”分類討論，還是用“參變分離法”化給定函數？尤其是做壓軸題時，一旦所確定的方法不合適，不光耗時耗力，而且想重新改正時發現時間已來不及.那么涉及具體問題時，我們如何“因題制宜”的解決，下面筆者以三個例題加以說明：

1 例題分析

例1已知函數f(x)=x-ln(x+1)，若對于任意的x∈(-1,0]，總有f(x)≥ax2，試求實數a的取值范圍.

解析設g(x)=f(x)-ax2=x-ln(x+1)-ax2，

則g(x)≥0在(-1,0]上恒成立，

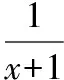
若a=0，則g′(x)≤0在(-1,0]上恒成立，

即g(x)在(-1,0]上單調遞減，

g(x)min=g(0)=0，g(x)≥0符合題意；

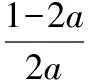
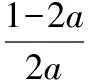
g′(x)≤0在(-1,0]上恒成立，

即g(x)在(-1,0]上單調遞減，

g(x)min=g(0)=0，g(x)≥0符合題意；

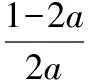
g′(x)≤0在(-1,0]上恒成立，

g(x)在(-1,0]上單調遞減，

所以g(x)min=g(0)=0，g(x)≥0符合題意；

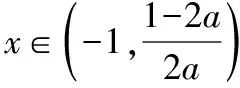
因此g(x)minlt;g(0)=0，不符題意.

2 例題再思考

上面兩個例題通過分析所給不等式的結構得出比較容易解決問題的通法.波利亞對解題過程有著精辟的論述：不斷地變換你的問題，我們必須一再地變化它，重新敘述它，變換它，直到最后成功地找到某些有用的東西為止.其實解決不等式恒成立問題中有的只能用或更適合用某一種，而有的兩種都可以.比如以上兩個例題，其實兩種方法都可以，只不過采取方法不同，導致難易程度有區別.

顯然，此法難點在于部分截取構造函數二次求導以及洛必塔法則的使用.

此例若用“函數法”難度增大不小，尤其是不等式的處理，不是解出關于k的不等式，而是通過換元得出其小于0恒成立，避免解“超越不等式”，但技巧性強，學生不易想到.

3 拓展延伸

“死板地硬套所選擇的模型乃是愚笨的，這是思維惰性的一種表現”.法無定法，掌握基本方法的基礎上靈活變通地分析問題、解決問題是我們的方向.一個知識、一種方法的學習更重要的意義在于思想的滲透，思維的訓練.

例3(2012·全國高考21題改編)已知a,b∈R，且ex+1≥ax+b對x∈R恒成立，則ab的最大值是

( )

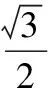
解析1由已知條件得b≤ex+1-ax.

(ⅰ)若alt;0，則x→-∞時，ex+1-ax→-∞，不等式不恒成立；

(ⅱ)若a=0，則ab=0；

(ⅲ)若agt;0，由b≤ex+1-ax得ab≤aex+1-a2x，

設f(x)=aex+1-a2x，f′(x)=aex+1-a2=a(ex+1-a)，令f′(x)=0，得x=lna-1，當x∈(-∞,lna-1)時，f′(x)lt;0，f(x)單調遞減；當x∈(lna-1,+∞)時，f′(x)gt;0，f(x)單調遞增，則f(x)min=f(lna-1)=2a2-a2lna.

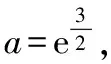
點評本題的求解最值問題涉及雙參數，而且兩個參數都沒有一些明顯的限制條件，針對雙參數一方面是配湊分離出所要求的ab這個整體的不等關系；另一方面是對參數的分類討論.

解析2考慮本題是選擇題的特點，遵循“小題小做，小題巧做”的原則，根據不等式的特點，將不等式兩側變形為初等函數，畫初等函數圖象，用數形結合的思想解題.我們不妨稱為“部分參變分離法”.

如圖，作f(x)=ex+1和g(x)=ax+b的圖象，由圖可知，要使不等式恒成立，則a≥0.

若a=0，則g(x)=b，原不等式恒成立?b≤0，此時ab=0.

若agt;0，如圖，求ab的最大值分兩步，第一步假定a的值不變，g(x)是隨著b的變化而變化的平行直線系.

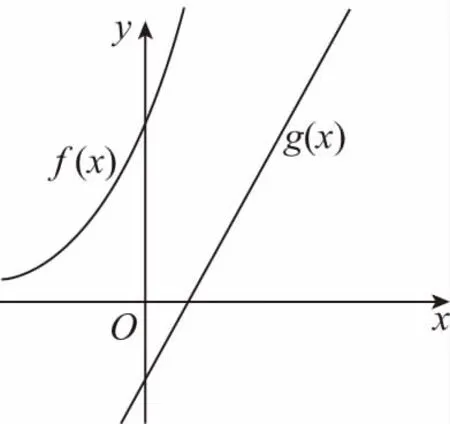
點評“部分參變分離”，將代數問題幾何化，數形結合，利用初等函數的圖象變化直觀判斷解決問題，節省時間，提高能力.

4 小結

“一個專心的認真備課的老師能夠拿出有意義但又不太復雜的題目去幫助學生發掘問題的各個方面，使得通過問題的解決，好像通過一道門戶，把學生引入一個完整的理論領域.”解決不等式恒成立問題到底是進行分類討論還是參變分離，需要在觀察和分析的基礎上獲得，當然也要有解題經驗的積累.

本文中解不等式恒成立問題在方法的選取上要注意，“函數法”重點是求導以后對參數的分類討論，參數的不同取值范圍對于導數的正負要容易判斷；“參變分離法”一是盡量使參變分離容易，要避免討論，二是分離以后所得的給定函數的最值能相對容易地求出來.

河北省定州中學)