特殊位置助解定點定角定值

甘肅 魏正清

特殊位置助解定點定角定值

甘肅 魏正清

解析幾何中的定點、定角、定值問題，是高考考查的核心題型之一，是多年高考經久不衰的熱點.這類問題常常以直線與圓錐曲線的位置關系為載體,以參數處理為核心,需要綜合運用函數、方程、不等式、平面向量等諸多數學知識，以及數形結合、分類討論等多種數學思想方法進行求解,解法一般來說都比較單一，雖然有通法可循，但運算量大且過程很繁瑣，如何化繁為簡，減少運算量，有效突破這一人人都頗感棘手的問題，是值得研究的課題，也是追求數學簡潔美的根本要求.本文另辟蹊徑，從特殊情形入手，先猜后證，給出處理解析幾何中定點、定角、定值問題的簡化策略.

1.定點問題

分析：如圖，探索以AB為直徑的圓是否恒過平面內一定點，通常都是先求出以AB為直徑的圓方程，再利用圓系的有關知識尋求定點，難度過大，不易上手.如果尋求特殊的圓，先猜后證，就能化繁為簡，將問題迎刃而解.

解：假設存在定點T(x0,y0)滿足題意，設A(x1,y1),B(x2,y2).

當直線m的斜率不存在時，直線m的方程為x=0，易知A(0,1),B(0,-1)且以AB為直徑的圓C1的方程是x2+y2=1；

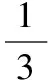
將圓C1與圓C2的方程聯立可得交點T(0,1).

以下只需驗證當直線m的斜率存在時，也符合題意.

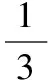
即當直線m的斜率存在時，以AB為直徑的圓也過定點T(0,1).

綜上所述，存在定點T(0,1)滿足題意.

【評注】證明某動曲線過平面內一定點，若從特殊情形入手，尋求符合題意的兩條曲線，求出這兩條曲線的交點，進而猜得定點，再加以驗證就可將問題圓滿解決.

2．定角問題

【例2】若點E在拋物線C：y2=2x上，且縱坐標為2，經過點(2,0)的直線l與拋物線C交于A,B兩點(不同于點E)，直線EA,EB分別交直線x=-2于點M,N，O為原點，求證：∠MON為定值.

分析：如圖，證明∠MON為定值，通常是驗證 tan∠MON的值為定值，這就需要將tan∠MON的求解轉化為直線的傾斜角，進而轉化為直線的斜率問題解決，這樣處理既要尋求∠MON與某兩條直線的傾斜角的關系，還要利用兩角和與差的正切公式，問題方能得以解決，過程繁且不說，運算量還很大.如果取特殊點，先猜出∠MON的值，再進行驗證，則有意想不到的收獲.

解：易知點E(2,2)，設直線l：y=k(x-2).

由直線l與拋物線C交于A(x1,y1),B(x2,y2)兩點，

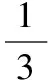
直線EB方程為y-2=2(x-2)，令x=-2得N(-2,-6).

【評注】證明一個角為定角，如果從特殊情形入手，求出符合條件的角的大小，再加以驗證，則可有效簡化過程，巧妙解決問題.

3．定值問題

分析：探索正數λ，負數m，使得∠QC2M=λ∠QMC2成立，按照正常思維實在是無從著手的，但若從極端情形入手，先猜出正數λ與負數m的值，再進行驗證，定會柳暗花明.

解：如圖設Q(x0,y0)(x0≥1,y0gt;0)，

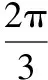
以下證明，當λ=2,m=-1時，恒有∠QC2M=2∠QMC2.

故存在λ=2,m=-1，使得∠QC2M=2∠QMC2.

【評注】探索某代數式的值為定值，若能另辟蹊徑，從特殊情形入手，先猜后證，定是別有洞天.

甘肅省臨澤一中)