研究解析幾何中直線平行的三個視角
安徽 阮 飛
研究解析幾何中直線平行的三個視角
安徽 阮 飛
解析幾何中的兩直線平行問題是一類既基本而又綜合性強的高考熱點問題.如果同學們能夠做到正確理解概念,弄清相關結論的推導過程、功能及使用條件,就能輕松快速的解決此類問題.本文主要介紹處理此類問題的三個視角,僅供大家參考.
一、利用兩條直線的斜率
【例1】如圖,已知兩條拋物線E1:y2=2p1x(p1gt;0)和E2:y2=2p2x(p2gt;0),過原點O的兩條直線l1和l2,l1與E1,E2分別交于A1,A2兩點,l2與E1,E2分別交于B1,B2兩點.求證:A1B1∥A2B2.
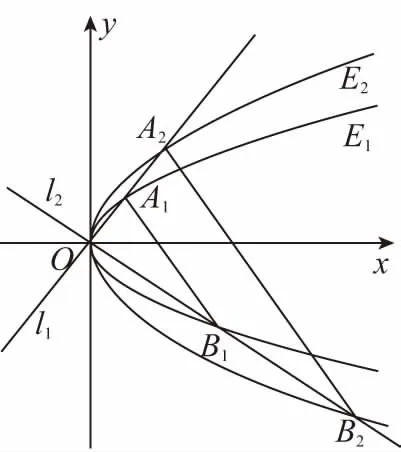
【證明】A1,A2兩點在過原點的直線l1上,
可設A1(x1,y1),A2(mx1,my1)(x1gt;0,mgt;0),
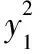
同理可設B1(x2,y2),B2(nx2,ny2)(x2gt;0,ngt;0),

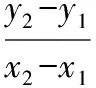
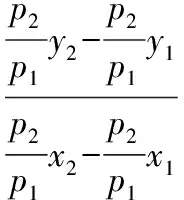
所以kA1B1=kA2B2,即A1B1∥A2B2.
②當x2-x1=0時,A1B1⊥x軸,A2B2⊥x軸,
故A1B1∥A2B2.
綜合①②可知,A1B1∥A2B2.
【評注】對于斜率都存在且不重合的兩條直線l1,l2,即若l1:y=k1x+b1,l2:y=k2x+b2,則l1∥l2?k1=k2,b1≠b2;特別地,當直線l1,l2的斜率都不存在且不重合時,l1與l2平行.此視角思路清晰,關鍵在斜率是否存在的討論和點的坐標、斜率的計算.
【變式】若直線x+(2a-1)y-1=0與(2a-2)x-(4a-2)y+3=0平行,則實數a的值為________.



二、利用兩條直線的方向向量或法向量
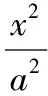
【證明】A1,A2兩點在直線l1上,
可設A1(x1,y1),A2(mx1,my1)(mgt;0),
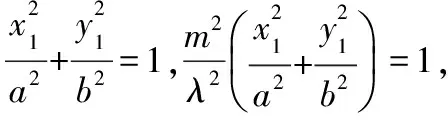
同理可設B1(x2,y2),B2(nx2,ny2)(ngt;0),且n=λ,
所以A2(λx1,λy1),B2(λx2,λy2),
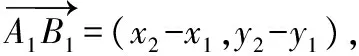
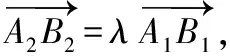
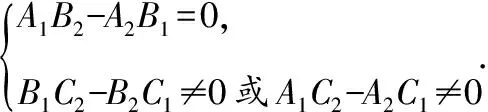
我們把與直線垂直的非零向量叫做直線的法向量,直線的法向量不唯一.直線Ax+By+C=0一定有一個法向量是(A,B);直線y=kx+b一定有一個法向量是(k,-1).不重合的兩條直線平行的充要條件是它們的法向量平行.
向量視角處理解析幾何問題往往自然簡潔.張奠宙先生說:“我們知道‘點’是不能‘計算’的.但是引入了坐標,并把點看作位置向量,就可以計算了;向量可以和‘數’相乘,兩個向量可以加減,以及有數量積等等,引入向量,能夠精中求簡,‘以簡馭繁’……”
【變式】已知直線l1:nx+8y+2=0和直線l2:2x+ny+1=0平行,求n的值.
【解析】(法1)直線l1:nx+8y+2=0,l2:2x+ny+1=0的一個法向量分別是n1=(n,8),n2=(2,n),
因為l1∥l2,所以n1∥n2,則n2-16=0,所以n=±4,
當n=4時,直線l1:4x+8y+2=0與直線l2:2x+4y+1=0重合,故n=-4.
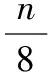
當n=4時,直線l1:4x+8y+2=0與直線l2:2x+4y+1=0重合,故n=-4.
三、利用平面幾何知識
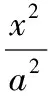
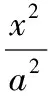
同理可得曲線E2的極坐標方程:

又A1,A2兩點在直線l1上,
可設A1(ρ1,α1),A2(ρ2,α1),ρ1=|OA1|,ρ2=|OA2|.
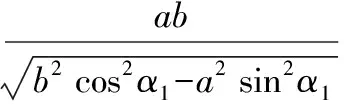
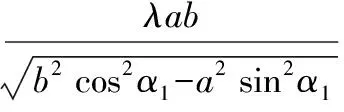
即ρ2=λρ1
所以|OA2|=λ|OA1|,同理可得|OB2|=λ|OB1|,
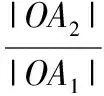
由平面幾何知識易知A1B1∥A2B2.
【評注】引理:如果一條直線截三角形的兩邊(或兩邊的延長線)所得的對應線段成比例,那么這條直線平行于三角形的第三邊.證明兩直線平行還可以通過證它們同垂直(或同平行)于第三條直線、被第三條直線截得的同位角相等(或內錯角相等,或同旁內角互補)等平面幾何方法.
解析幾何是用代數方法研究幾何問題,但解題時不能僅使用代數方法,應重視運用平面幾何知識簡化和轉化題目中的條件,這也是近年高考試題考查的一個方向.
【變式】已知兩條曲線E1:x2+y2=1(xgt;0)和E2:x2+y2=4(xgt;0),過原點O的兩條不同直線l1和l2,l1與E1,E2分別交于A1,A2兩點,l2與E1,E2分別交于B1,B2兩點.求證:A1B1∥A2B2.
【證明】依題意|OA1|=|OB1|=1,|OA2|=|OB2|=2,
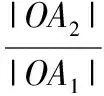
在△OA2B2中,由平面幾何知識知A1B1∥A2B2.
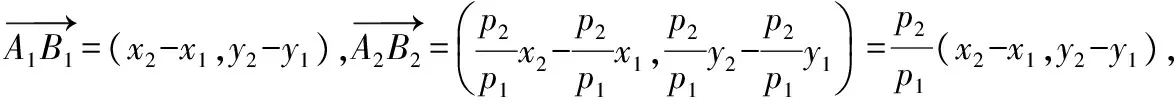
安徽省太和中學)

