我為高考模考命題
——談概率統計題的命制

新疆 徐 波

我為高考模考命題
——談概率統計題的命制

新疆 徐 波

概率統計試題在高考試卷中占了一道大題(12分)，歷來為兵家(考生)必爭之地，概率統計試題的核心是考查考生的數據處理能力，那么，什么是數據處理能力呢？對比2016年和2017年高考考綱后發現,對數據處理能力的要求已經發生了悄然的變化：

2016年高考考綱中對數據處理能力的要求是：

“數據處理能力：會收集、整理、分析數據,能從大量數據中抽取對研究問題有用的信息,并做出判斷.

數據處理能力主要依據統計或統計案例中的方法對數據進行整理、分析，并解決給定的實際問題.”

2017年高考考綱中對數據處理能力的要求是：

“數據處理能力：會收集、整理、分析數據,能從大量數據中抽取對研究問題有用的信息,并做出判斷.

數據處理能力主要是指針對研究對象的特殊性，選擇合理的收集數據的方法，根據問題的具體情況，選擇合適的統計方法整理數據，并構建模型對數據進行分析、推斷,獲得結論.”

對比2016年和2017年高考考綱中對數據處理能力的要求，我們發現：2017年高考考綱中對數據處理能力的要求提高了，如果說2016年考綱對數據處理能力的要求是“會用模型”，那么2017年考綱對數據處理能力的要求就是“根據問題的具體情況，選擇合適的統計方法，構建模型對數據進行分析、推斷,獲得結論.”也就是說對模型的要求提高了.

由于筆者有多年參與烏魯木齊市高三診斷性測試命題的經歷和經驗，其中的概率統計題的命制大多是由筆者負責完成的，在對歷年高考真題的研究和在烏魯木齊市高三診斷性測試命題實踐中筆者深切體會到用樣本估計總體、用樣本的頻率分布估計總體的概率分布，這是概率統計這門課程的基本思想，而數據處理能力又是解決概率統計題的關鍵，所以，下面筆者就選擇幾道我們原創的烏魯木齊市高三診斷性測試試題來進行舉例說明，同時，也想把這些原創的試題介紹給大家共享和交流.

一、含有兩個隨機變量的題型定式

通過研究歷年高考試題，我們發現在一個題目里總是會設置兩個隨機變量X和Y，其中X是作為已知條件呈現出來的(呈現的方式有頻率分布直方圖、頻率分布表、莖葉圖等)，而Y是與X有關聯的一個量，Y是X的函數，Y與X的這種函數關系的呈現方式可以是解析式、也可以是表格.Y就是用來出題的，題目當中的問題就是針對Y這個量來出的.這是這些年高考題的一個基本的模式和套路.

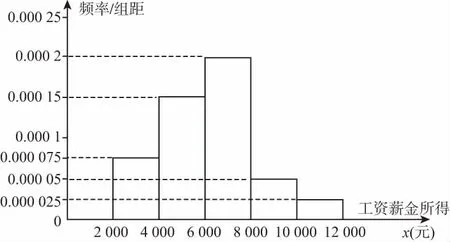
【例1】(2014年烏魯木齊市高三第一次診斷性測試理科第19題)某市共有100萬居民的月收入是通過“工資薪金所得”得到的，如圖是抽樣調查后得到的工資薪金所得X的頻率分布直方圖，工資薪金個人所得稅稅率表如表所示.表中“全月應納稅所得額”是指“工資薪金所得”減去3 500元所超出的部分(3 500元為個稅起征點，不到3 500元不繳稅).

工資個稅的計算公式為“應納稅額”=“全月應納稅所得額”乘以“適用稅率”減去“速算扣除數”.

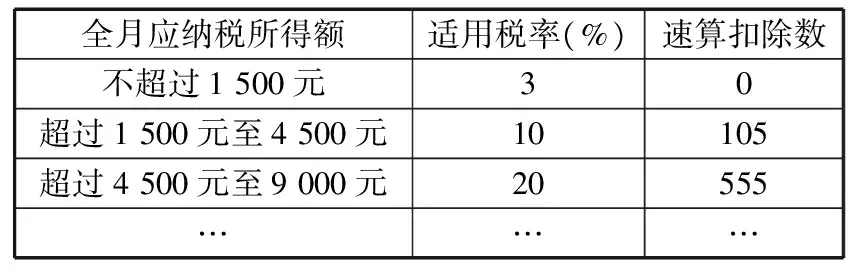
全月應納稅所得額適用稅率(%)速算扣除數不超過1500元30超過1500元至4500元10105超過4500元至9000元20555………

例如：某人某月“工資薪金所得”為5 500元，則“全月應納稅所得額”為5 500-3 500=2 000元，應納稅額為2 000×10%-105=95(元)

在直方圖的工資薪金所得分組中，以各組的區間中點值代表該組的各個值，工資薪金所得落入該區間的頻率作為x取該區間中點值的概率.

(Ⅰ)試估計該市居民每月在工資薪金個人所得稅上繳納的總稅款；

(Ⅱ)設該市居民每月從工資薪金所得交完稅后，剩余的為其月可支配額y(元)，試求該市居民月可支配額y的數學期望.

【命題構思意圖】出題的時候，我們首先要構思兩個有關聯的隨機變量X和Y，因此就想到了居民的月收入X和他的納稅額Y，二者之間的關系由稅率表來呈現(這個關系其實是一個分段函數，而且這個分段函數模型在人教A版必修一教材中出現過，源于課本，對所有的同學來說背景是公平的)，居民的月收入X是用來作為已知條件給出的，呈現方式我們首選還是用頻率分布直方圖，那么，題目要出的問題就針對Y這個量來出，可以出Y的分布列、Y的期望等問題，但都覺得落入了俗套，所以最后我們還是出了求Y的總量這樣的問題.

另外，用樣本估計總體，用樣本的頻率分布估計總體的概率分布，這是統計這門課程的基本思想，因此，概率統計試題的命制不能離開這個主航道，所以我們在題目中以抽樣調查后得到的工資薪金所得X的頻率分布直方圖來作為總體該市100萬居民的月收入的概率分布，就是要體現統計這門課程的這一基本思想.

最后，如何用樣本去估計總體？如何用樣本的頻率分布直方圖去估計總體的概率分布？這是一個具體的操作技術層面的事情，在直方圖中，往往以各組的區間中點值代表該組的各個值，以樣本值落入該區間的頻率作為總體取該區間中點值的概率，這是在頻率分布直方圖中經常采用的一種數據處理的手段，所以我們在題目中也希望能夠制造機會，使考生展示這樣的一種數據處理能力.

解：(Ⅰ)工資薪金所得的5組區間的中點值依次為3 000,5 000,7 000,9 000,11 000，x取這些值的概率依次為0.15,0.3,0.4,0.1,0.05，算得與其相對應的“全月應納稅所得額”依次為0,1 500,3 500,5 500,7 500(元)，按工資個稅的計算公式，相應的工資個稅分別為：

0(元)，

1 500×3%-0=45(元)，

3 500×10%-105=245(元)，

5 500×20%-555=545(元)，

7 500×20%-555=945(元)；

∴該市居民每月在工資薪金個人所得稅上繳納的總稅款為

(45×0.3+245×0.4+545×0.1+945×0.05)×106=2.1325×108(元)；

(Ⅱ)這5組居民月可支配額y取的值分別是Y1,Y2,Y3,Y4,Y5，

Y1=3 000(元)；

Y2=5 000-45=4 955(元)；

Y3=7 000-245=6 755(元)；

Y4=9 000-545=8 455(元)；

Y5=11 000-945=10 055(元)；

∴Y的分布列為

Y300049556755845510055P0．150．30．40．10．05

∴該市居民月可支配額的數學期望為

E(Y)=3 000×0.15+4 955×0.3+6 755×0.4+8 455×0.1+10 055×0.05=5 986.75(元)

【解法指導】學生解這種含有兩個隨機變量的題型問題時，首先在審題時就要自覺的去捕捉題目里設置的是哪兩個隨機變量X和Y，其中X是已知的，它的呈現方式是哪種(呈現的方式有頻率分布直方圖、表格、莖葉圖等)，Y是用來出題的，題目針對Y這個量出了一個什么樣的問題，而Y與X的關系的呈現方式又是什么.要把這些題目中的要素迅速地提煉出來，然后進行數據處理.本題在具體進行數據處理時，在直方圖中以各組的區間中點值代表該組的各個值、以樣本值落入該區間的頻率作為總體取該區間中點值的概率，這種手法是在頻率分布直方圖中經常采用的一種數據處理的手段，復習中希望考生牢固掌握在頻率分布直方圖中如何求中位數、均值、方差這些基本的數據處理能力.

【命題反思】本題第二問中又設計了一個量“該市居民月可支配額”，這樣一來本題中就貫穿了三個量：月工資薪金所得→全月應納稅所得額→月可支配額，這樣就顯得環節多了一點，一般來說高考題中只設置兩個相關聯的隨機變量，這兩個隨機變量X和Y以一種函數關系呈現出它們彼此間的聯系，本題設置了三個隨機變量，就顯得略多了一點，有重復考查之嫌.

二、注重對重要的概率模型進行考查

數據處理能力常常需要在“會用模型”這樣一個平臺上去展示，我們中學學習的超幾何分布、二項分布、正態分布都是最常用、最經典的概率模型，所以，無論是高考還是模考，都會對這些重要的概率模型著重進行考查.

【例2】(2017年烏魯木齊市高三第一次診斷性測試理科第19題)某地十余萬考生的成績近似地服從正態分布，現從中隨機地抽取了一批考生的成績，將其分成6組：第一組[40,50)，第二組[50,60)，……，第六組[90,100]，作出頻率分布直方圖如圖所示.

(Ⅰ)用每組區間的中點值代表該組的數據，估算這批考生的平均成績和標準差(精確到個位)；

(Ⅱ)以這批考生成績的平均值和標準差作為正態分布的均值和標準差，設成績超過93分的為“優”，現在從總體中隨機抽取50名考生，記其中“優”的人數為Z，試估算Z的期望．

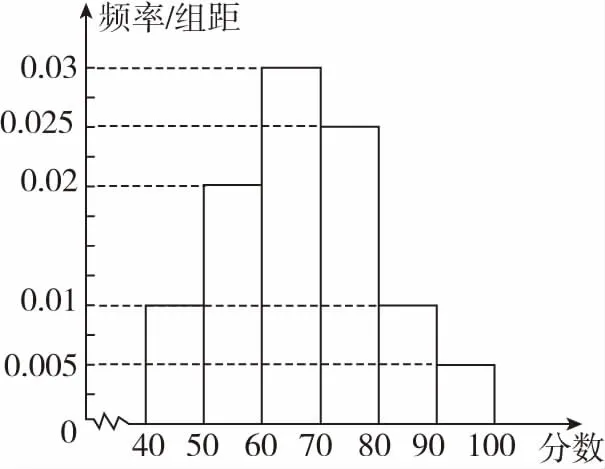
附：

若X～N(μ,σ2)，

則P(μ-σlt;Xlt;μ+σ)=0.683，

P(μ-2σlt;Xlt;μ+2σ)=0.954,

P(μ-3σlt;Xlt;μ+3σ)=0.997.

【命題構思意圖】我們想設置一個情景來考查我們中學學習的超幾何分布、二項分布、正態分布這些重要的概率模型，但是我們還是不忘用樣本的頻率分布估計總體的概率分布這一根本思想，因此我們設置出抽取一批考生的成績，作出頻率分布直方圖這個背景(這相當于抽取了一個樣本)，再用這個樣本去估計總體正態分布的兩個重要參數(均值和標準差)，以此來確定出這個總體正態分布.而正態分布的考查只限于P(μ-σlt;Xlt;μ+σ)=0.683，P(μ-2σlt;Xlt;μ+2σ)=0.954，P(μ-3σlt;Xlt;μ+3σ)=0.997這三個概率值，因此，我們在出題的時候就要精準地瞄準這些臨界值才行,這樣就考查了正態分布這個概率模型，但是，我們還希望考查超幾何分布、二項分布這些重要的概率模型，所以我們就出了“現在從總體中隨機抽取50名考生，記其中‘優’的人數為Z”這一問題，這個問題既可以納入超幾何分布概率模型、又可以納入二項分布這個概率模型，但是我們故意在題目出示的已知條件“某地十余萬考生的成績近似地服從正態分布”里，模糊了總數“十余萬考生”，這樣你要想用超幾何分布概率模型來做，計算上就行不通，最后就被“逼”到二項分布這個概率模型上來了.

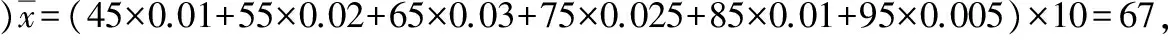
s2=(45-67)2×0.01×10+(55-67)2×0.02×10+(65-67)2×0.03×10+(75-67)2×0.025×10+(85-67)2×0.01×10+(95-67)2×0.005×10=166，

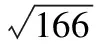
(Ⅱ)依題意X～N(67,13)，

P(μ-2σlt;xlt;μ+2σ)=P(41lt;xlt;93)=0.954，

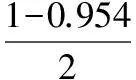
∵Y～B(50,0.023)，∴E(Y)=50×0.023=1.15.

【解法指導】本題要求考生牢固掌握在頻率分布直方圖中如何求均值、方差這些基本的數據處理能力，能夠對超幾何分布、二項分布這些概率模型進行識別辨析和應用.

【命題反思】本題在“用樣本的頻率分布估計總體的概率分布”這樣一個背景下設計考查了正態分布這個概率模型，但是，我們還希望考查超幾何分布、二項分布這些重要的概率模型，所以我們就設置了“現在從總體中隨機抽取50名考生，記其中‘優’的人數為Z”這一問題，這個問題既可以納入超幾何分布概率模型、又可以納入二項分布這個概率模型，但是我們故意在題目出示的已知條件“某地十余萬考生的成績近似地服從正態分布”里，模糊了總數“十余萬考生”，這樣你要想用超幾何分布概率模型來做，計算上就行不通，最后就被“逼”到二項分布這個概率模型上來了.總之，對超幾何分布、二項分布這些概率模型的辨析和應用是非常重要的.

三、注重對重要的統計案例進行考查

數據處理能力還需要針對研究對象的特殊性，根據問題的具體情況，選擇合適的統計方法整理數據，并構建模型對數據進行分析、推斷,獲得結論.我們中學學習的獨立性假設檢驗、回歸分析就是最常用、最經典的兩個統計案例，所以，無論是高考還是模考，都會對這些重要的統計案例著重進行考查.

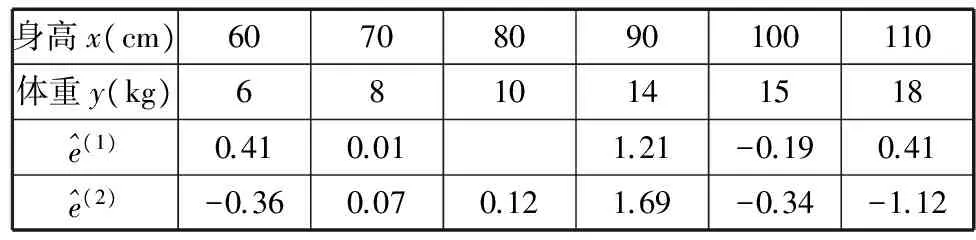
身高x(cm)60708090100110體重y(kg)6810141518＾e(1)0．410．011．21-0．190．41＾e(2)-0．360．070．121．69-0．34-1．12

(Ⅰ)求表中空格內的值；

(Ⅱ)根據殘差比較模型①，②的擬合效果，決定選擇哪個模型；

(Ⅲ)殘差大于1 kg的樣本點被認為是異常數據，應剔除，剔除后對(Ⅱ)所選擇的模型重新建立回歸方程.

(結果保留到小數點后兩位)

【命題構思意圖】我們中學學習的回歸分析是最常用、最經典的一個統計案例，因此，我們想設置一個情景來考查這個統計案例，這首先需要構造兩個“相關變量”，我們還是依據課本和學生都熟悉的生活經驗，選擇了身高與體重這兩個量，再結合人教A版課本選修2-3上的殘差分析的有關內容，我們首先要求考生對兩個回歸模型進行比較和評判，作出取舍和選擇，最后剔除異常數據后再對所選擇的那個模型重新建立回歸方程.以達到優化回歸方程的目的.在這樣一個完整的過程中來考查考生對回歸模型的理解掌握程度和數據處理能力.

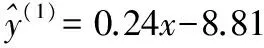
(Ⅱ)模型①殘差的絕對值的和為0.41+0.01+0.39+1.21+0.19+0.41=2.62，

模型②殘差的絕對值的和為0.36+0.07+0.12+1.69+0.34+1.12=3.7，

2.62lt;3.7，所以模型①的擬合效果比較好，選擇模型①.

(Ⅲ)殘差大于1 kg的樣本點被剔除后，剩余的數據如下表

身高x(cm)607080100110體重y(kg)68101518＾e(1)0．410．01-0．39-0．190．41

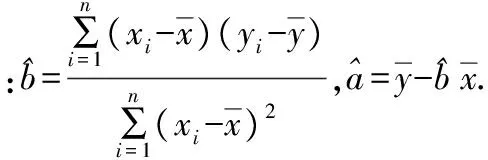
【解法指導】本題要求考生對建立回歸模型、利用回歸模型預測、評價回歸模型、殘差分析的方法等有關內容都有所了解，在這樣一個完整的過程中來考查考生對回歸模型的理解掌握程度和數據處理能力.雖然只是套公式做題，但是對計算能力的要求還是較高的，平時復習時養成把公式中的項目列成表再代入計算的習慣，按程序性知識的學習機制進行學習.

新疆兵團二中)