從幾個不同角度思考一道平面向量題
江蘇 張路民
從幾個不同角度思考一道平面向量題
江蘇 張路民
最近筆者聽了一堂高三一輪復習課《平面向量基本定理和坐標表示》,課堂上師生們在共同探討一道習題時,經歷了一些波折也遇到了一些困難,其中有些思路中途夭折未能進行到底.筆者細細琢磨了一番,覺得甚是有趣,現將筆者的一些想法分享如下:
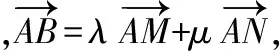
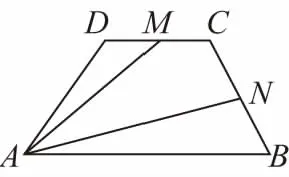
分析:這道題考查的知識點是平面向量的基本定理,研究的策略無非是基底法與幾何法.課堂上學生從不同角度進行思考,但最終不是因為過程繁瑣就是思路卡殼難以進行到底.
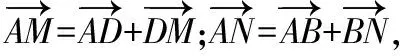
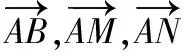
下面筆者就這個問題分別從坐標法、基底法和幾何法三個不同的角度對本題加以詮釋.
一、坐標法
向量是既研究大小又研究方向的量,利用坐標法解決向量問題往往能夠使問題簡化,另外我們都知道解決填空題有別于解答題,只要能算出答案就可以,其中特值特例就是一種非常有效且簡易的手段.本題可以將問題特殊化即把梯形看成直角梯形,為使計算方便還可以將邊長取特殊值.
解法1:將梯形ABCD看成直角梯形,且設AB=4,AD=2,如圖建立直角坐標系,結合2DC=AB,M,N分別是DC,BC中點,則A(0,0),B(4,0),D(0,2),C(2,2),M(1,2),N(3,1).
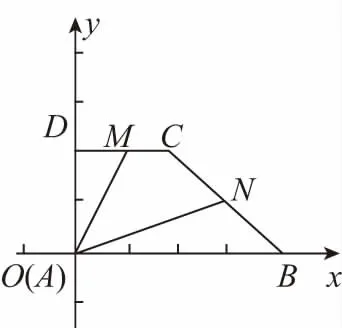
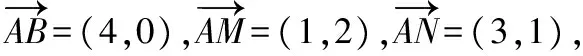
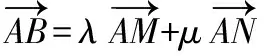
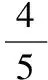
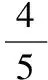
小結:本題巧妙地利用了梯形的任意性,采用特殊代替一般的處理原則,使問題解決簡捷快速.因此,這一方法對于解決選擇題和填空題非常有效,但此方法處理并不具有普遍性,需要解題者自己去把握與權衡.
二、基底法
平面向量基本定理:如果e1、e2是同一平面內不共線的兩個向量,那么對于這個平面內的任一個向量a,有且只有一對實數λ1、λ2,使a=λ1e1+λ2e2.不共線的向量e1、e2叫做表示這一平面內的所有向量的一組基底.因此在具體操作過程中,選取哪兩個向量作為e1、e2以及如何用選取的e1、e2表示a,將是解決問題的關鍵,也是難點所在.
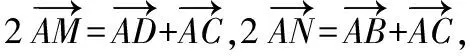
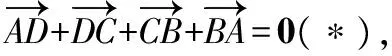
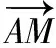
三、幾何法
向量題是高中數學的重點、熱點考點.解題時可以從數與形兩個角度考慮,代數法證明思維量小但計算量都較大.相對于代數法,幾何法的優勢在于直觀且計算量小,找到向量的幾何意義后,問題就能迎刃而解,它是求解向量問題的有效策略之一,對于運用幾何法解決向量題應該引起我們足夠的重視.
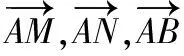
解法4:如圖,延長AN與DC的延長線交于點E.

因為DC∥AB,點N是BC的中點,
所以CEAB,AN=NE,即
又因為點M是DC中點且AB=2CD,
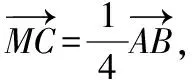

解法5:如圖,連接BD,連接MN并延長與AB的延長線交于點E.

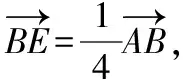
解法6:如圖,延長AM,BC交于點E,
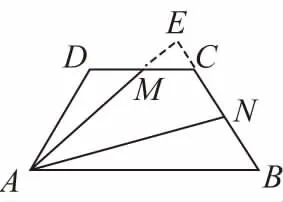
因為AB∥DC,且AB=2DC,
又點M為DC中點,所以AE=4ME,BE=4CE,




江蘇南京市大廠高級中學)

