類比·探究·結論
安徽 李昭平
類比·探究·結論
安徽 李昭平
由一事物的性質類比聯想到另一事物的相應性質,是近幾年高考出現的一種新題型.這種問題,往往融直觀想象、邏輯推理、數學運算等數學核心素養于一體,能有效考查學生的合情猜想、思維水平和綜合能力.一般涉及到結構上、概念上、次數上、元數上、方法上的類比和探究,常見的有平面向空間類比、橢圓向雙曲線類比、低次向高次類比、等差向等比類比、少元向多元類比等等.下面予以介紹,供參考.
1.平面向空間類比
【例1】我們知道:在平面幾何中,△ABC的三條中線相交于一點,這個點叫三角形的重心,并且重心分中線之比為2∶1(從頂點到對邊中點).據此,我們拓展到空間:把空間四面體的頂點與對面三角形的重心的連線叫空間四面體的中軸線,則四條中軸線相交于一點,這點叫此四面體的重心.類比上述命題,請寫出四面體重心的類似性質,并證明.
【思路】將三角形邊的中點類比到四面體面的重心,將三角形重心性質的證明方法類比到空間四面體中,利用相似三角形對應邊成比例.
【解析】四面體重心的性質:空間四面體的重心分頂點與對面三角形的重心的連線之比為3:1(從頂點到對面三角形的重心).
事實上:如圖,AE,BP為四面體的中軸線,P,E分別為△ACD,△BCD的重心,連接BE,AP并延長,交CD于點F,再連接PE.

因為AP∶PF=2∶1,BE∶EF=2∶1,
所以AP∶PF=BE∶EF,所以PE∥AB,
因此AG∶GE=BG∶GP=AB∶PE=3∶1.
【點評】一般地,平面上的“點、線、面”往往類比到空間上的“線、面、體”(元素類比),比如平面上的三角形類比到空間上的四面體,平面上的角類比到空間的二面角,三角形的中位線類比到空間四面體的中位面,三角形的外接圓類比到三棱錐的外接球等等;平面上的數量結構形式往往類比到空間上的數量結構形式(結構類比);平面上的“面積法”往往類比到空間上的“體積法”,平面上的“相似法”往往類比到空間上的“相似法”(方法類比).“將平面圖形的性質類比到空間,探求相應的空間圖形是否也有此類似的性質”,這是近幾年高考考查立體幾何出現的一種新題型.這種問題往往以平面圖形的性質及其證法為基礎,融探索、猜想、證明于一體,充分體現了新課改的理念.但要注意類比的結論不一定都正確,需要探究和證明.
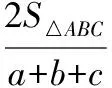
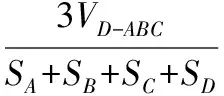
VO-ABC+VO-BCD+VO-CDA+VO-DAB=VD-ABC(O為內切球的球心)
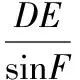

【答案】(Ⅰ)很容易證明,略去.
(Ⅱ)斜三棱柱各側面面積與它所對棱所對應的二面角的正弦的比相等.

2.橢圓向雙曲線類比
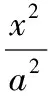
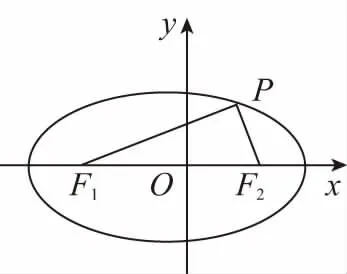

【思路】從橢圓問題的證法出發,結合雙曲線的定義,類比前行.
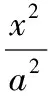

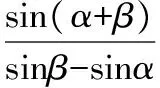


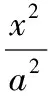
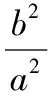



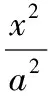

這就是橢圓焦點三角形的一個面積計算公式.類比上述方法,推導雙曲線焦點三角形的一個面積計算公式.
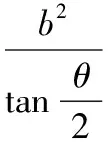

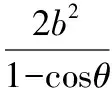

3.低次向高次類比
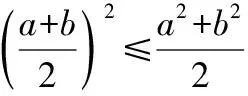
【思路】將字母a,b的次數升到3,仿上證明即可.
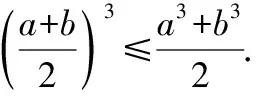


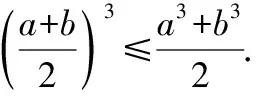
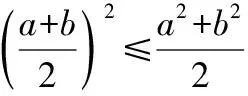
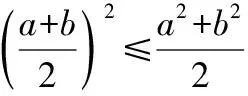


4.等差向等比類比

【思路】從等差數列、等比數列的內在聯系,以及和式的結構式出發進行類比聯想.

只證充分性(必要性易證,略去).
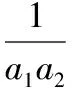



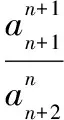

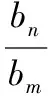
【訓練6】設數列{an}的前n項和為Sn,不難得到數列{an}為等差數列的充分必要條件:對任何n∈N*,都有Sn=An2+Bn(A,B是常數).證明不難,略去.由此向等比數列類比,寫出結論,并證明之.
【答案】結論:設數列a1,a2,…,an中的每一項都不為零,且前n項和為Sn,則數列{an}為公比非1的等比數列的充分必要條件:對任何n∈N*,都有Sn=kqn-k(k,q是非零的常數).
證明:只證充分性(必要性易證,略去).
當n≥2時,an=Sn-Sn-1=(kqn-k)-(kqn-1-k)=k(q-1)qn-1.
當n=1時,a1=S1=kq-k=k(q-1).
所以an=k(q-1)qn-1,n∈N*.
因此{an}是等比數列.
5.少元向多元類比

【思路】從已知不等式的結構特征進行類比聯想,推廣到三元以上.
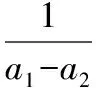
事實上,當n=3時,由已知不等式知,
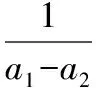
假設n=k(k≥3)時,不等式成立,即
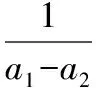
則當n=k+1時,
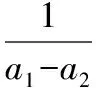
【點評】這里是將不等式中的三個字母拓展到n個字母,得到新的不等式,從中體會到類比的魅力.從少元向多元類比往往能拓展思維、發現新知,提高猜想和推理能力.比如x=1表示數軸上一個點,類比到二維空間就是單位圓x2+y2=1,再類比到三維空間就是單位球x2+y2+z2=1,如此等等.




安徽省太湖中學)

