非自治反映擴(kuò)散方程后項(xiàng)緊拉回吸引子的存在性

佘連兵, 王仁海

(1. 六盤水師范學(xué)院 數(shù)學(xué)與信息工程學(xué)院, 貴州 六盤水 553004; 2. 西南大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 重慶 400715)

非自治反映擴(kuò)散方程后項(xiàng)緊拉回吸引子的存在性

佘連兵1, 王仁海2

(1. 六盤水師范學(xué)院 數(shù)學(xué)與信息工程學(xué)院, 貴州 六盤水 553004; 2. 西南大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 重慶 400715)

給出了定義在Banach空間上的非自治過程存在唯一的后項(xiàng)緊的拉回吸引子的一個(gè)充分條件，運(yùn)用此理論證明了非自治反映擴(kuò)散方程在相對弱的假設(shè)條件下存在唯一的后項(xiàng)緊拉回吸引子.

非自治動(dòng)力系統(tǒng); 拉回吸引子; 后項(xiàng)緊性; 非自治反映擴(kuò)散方程

ut+λu-Δu=f(x,u)+g(t,x),x∈E,

(1)

其中,E是RN中的有界域,t≥s∈R,λgt;0且u(s,s,x)=u0.

關(guān)于非自治動(dòng)力系統(tǒng)的詳細(xì)介紹可見文獻(xiàn)[3,5].此外，為了方便后面的后項(xiàng)一致估計(jì)，把文獻(xiàn)[4]中的Gronwall型不等式寫成下面的具有非自治形式的后項(xiàng)Gronwall型不等式(這里對過去的時(shí)間取上確界).設(shè)y、y′、y1和y2是R上的局部可積函數(shù),且y、y1和y2是非負(fù)的，對于每個(gè)t∈R滿足

y′(s)+by(s)+y1(s)≤y2(s),s≤t.

(i) 若b∈R是一個(gè)給定的常數(shù)，則對于每一個(gè)t∈R和μgt;0有

(2)

(ii) 若b≥0是一個(gè)給定的常數(shù)，則對于每一個(gè)t∈R和μgt;0有

(3)

1 后項(xiàng)緊拉回吸引子理論

定義1.1設(shè)S(t,s):X→X,?t≥s是定義在Banach空間X上的一族映射,若對于任意的t≥r≥s有S(s,s)=idx，S(t,s)=S(t,r)S(r,s)，則稱S是X上的一個(gè)非自治過程.

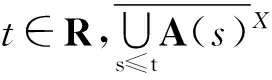
定義1.3設(shè)A={A(t)}t∈R是Banach空間X中的一個(gè)非自治集,對任意的t1,t2∈R,當(dāng)t1≤t2時(shí)，有A(t1)?A(t2),則稱A是單調(diào)遞增的；當(dāng)t1≤t2時(shí)，有A(t1)?A(t2),則稱A是單調(diào)遞減的.

定義1.4設(shè)S是定義在Banach空間X上的一個(gè)非自治過程,若X中的一個(gè)非自治集A={A(t)}t∈R滿足：

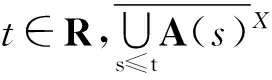
2)A是不變的，即S(t,τ)A(τ)=A(t),t≥τ;

3)A是拉回吸引的，即對于X中每個(gè)有界集D有

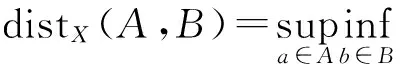
定理1.1設(shè)S是定義在Banach空間X上的一個(gè)非自治過程，若

(i) S在X上有一個(gè)單調(diào)遞增的有界閉吸收集K={K(t)}t∈R,

(ii)S是后項(xiàng)ω極限緊的,即

則S有一個(gè)后項(xiàng)緊的拉回吸引子A={A(t)}t∈R,其中κX(·)是文獻(xiàn)[3]中介紹的Kuratowski測度，

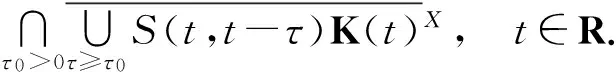
(4)

證明設(shè)B(X)是X中有界集的全體.條件(i)和(ii)滿足文獻(xiàn)[8]中的定理2.23,因此S有一個(gè)拉回吸引子A={A(t)}t∈R,其中A(t)由(4)式給出.

A(s)=ωX(K(s),s)=

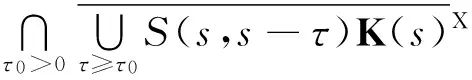
k(s)?k(t)?D,

(5)

讓τn→+∞當(dāng)n→+∞，由A的不變性和(5)式知

A(sn)=S(sn,sn-τn)A(sn-τn)?

S(sn,sn-τn)D,

(6)

由(6)式和yn∈A(sn)知，存在xn∈D,使得

yn=S(sn,sn-τn)xn, xn∈D.

(7)

因?yàn)棣觧→+∞當(dāng)n→+∞,所以存在Ngt;0使得當(dāng)n≥N時(shí)有τn≥τ1.又由(ii)知?εgt;0,D∈B(X)存在τ0gt;0使得

ε.

(8)

從而由(7)和(8)知

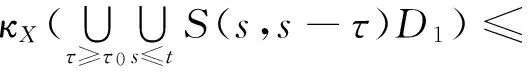
(9)

此外,容易證明以下性質(zhì)：

性質(zhì)2如果S在X上存在一個(gè)后項(xiàng)緊的拉回吸引子A,則A一定唯一的且是X中所有閉的拉回吸引集中最小的；

性質(zhì)3S在X中有一個(gè)單調(diào)遞增的有界的吸收集等價(jià)于S在X中有一個(gè)后項(xiàng)有界的吸收集.

2 后項(xiàng)緊拉回吸引子的存在唯一性

本章將證明方程(1)在相對弱的假設(shè)條件下存在唯一的后項(xiàng)緊拉回吸引子,為了方便計(jì)算，設(shè)c是變化的正常數(shù).

假設(shè)F設(shè)pgt;2,β1,β2,β3gt;0,f(·,·)∈C1(E×R,R)滿足

f(x,u)u≤-β1|s|p+ψ1, ψ1∈L2(E), (10)

|f(x,u)|≤β2|s|p-1+ψ2,ψ2∈L2(E),(11)

由于研究的是有界域,故ψi(i=1,2,3)也可以換成一般的常數(shù).

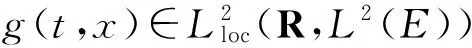
‖g(r,·)‖2drlt;∞, ?t∈R.(12)

此假設(shè)條件比文獻(xiàn)[5]中的假設(shè)條件弱,但仍然能得到想要的結(jié)果,這是因?yàn)槲墨I(xiàn)[5]做了如下假設(shè)：外力項(xiàng)是后項(xiàng)平移有界的,即

‖g(r,·)‖2drlt;∞,

?t∈R,agt;0,

(13)

且作者證明了(13)式與

‖g(r,·)‖2drlt;∞,

?t∈R,λgt;0

(14)

是等價(jià)的.因此容易得出假設(shè)G比假設(shè)(13)弱.

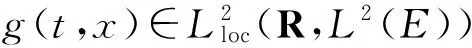
u(·,s,u0)∈C([s,+∞),L2(E))∩

(15)

特別地,u(s,s,u0)=u0,于是由適定性可以定義如下非自治過程S(·,·):L2(E)→L2(E):

S(t,t-τ)u0=u(t,t-τ,u0),
?u0∈L2(E),τ≥0.

(16)

定理2.1若假設(shè)F和G成立,則?t∈R,u0∈D∈B(L2(E)),存在一個(gè)τ0=τ0(D)gt;3,使得對?τ≥τ0有

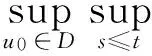
其中

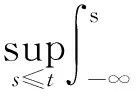
此外，S在L2(E)上有一個(gè)單調(diào)遞增的有界吸收集.

證明讓(1)式與u做內(nèi)積可得

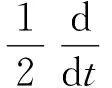
(20)

由Young不等式及(10)式可知(20)式右邊滿足

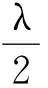
(21)

由(20)和(21)式知

(22)

在[s-τ,s]上對(22)式用經(jīng)典的Gronwall不等式,并由u(s-τ,s-τ,u0)=u0得

由u0∈D∈B(L2(E))，于是存在一個(gè)τ0=τ0(D)gt;3使得當(dāng)τ≥τ0時(shí)有

‖u(s,s-τ,u0)‖2+

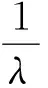
(24)

于是(17)和(18)式成立.記

H(t)={w∈L2(E):‖w‖2≤c(1+M(t))},

t∈R.

(25)

由假設(shè)G知M(t)是有界且單調(diào)遞增的,故由(17)式知H={H(t)}t∈R是L2(E)上的一個(gè)單調(diào)遞增的有界閉吸收集.

引理2.1若假設(shè)F和G成立,對?t∈R,u0∈D∈B(L2(E)),則存在一個(gè)τ0≥3,使得對?τ≥τ0有

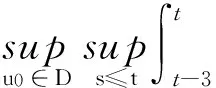
ceλt(1+M(t)).

(26)

證明將(1)式與|u|p-2u做內(nèi)積,可得

(27)

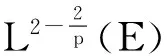
(28)

由Young不等式知

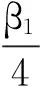
(29)

于是由(27)～(29)式知

c‖g(t,·)‖2+c.

(30)

當(dāng)μ=1,b=0時(shí)，對(30)式運(yùn)用后項(xiàng)Gronwall型不等式,并由(18)和(19)式知當(dāng)τ≥τ0gt;3時(shí)有

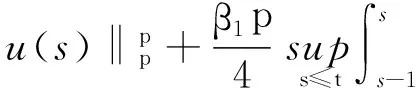
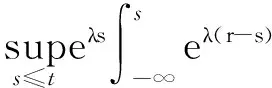
ceλt(1+M(t)),

(31)

于是(26)式成立.

下面估計(jì)解在H1(E)上的吸收性.

引理2.2若假設(shè)F和G成立,則對?t∈R,u0∈D∈B(L2(E)),存在一個(gè)τ0≥3,使得對?τ≥τ0有

ceλt(1+M(t)).

(32)

證明讓(1)式與ut做內(nèi)積可得

(33)

由Young不等式及(10)式可得

(35)

由(33)～(35)式得

(36)

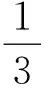
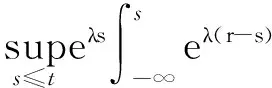
ceλt(1+M(t)),

(37)

于是(32)式成立.

定理2.2若假設(shè)F和G成立,則(16)式中的非自治過程S是后項(xiàng)ω極限緊的.

證明定義一個(gè)時(shí)間依賴的集合

其中D是L2(E)上的任意有界集，容易看出F(τ)關(guān)于τ是單調(diào)遞減的，由引理2.2知,存在τ0gt;3，當(dāng)τ≥τ0時(shí)有F(τ)是H1(E)中的有界集,由Sobolev緊嵌入定理知F(τ)是L2(E)中的預(yù)緊集,故由文獻(xiàn)[3]中的引理2.7(c)可知?εgt;0,κL2(E)F(τ)lt;ε,因此

(38)

所以(16)式中的非自治過程S是后項(xiàng)ω極限緊的.

定理2.3在L2(E)中,非自治的反映擴(kuò)散方程(1)在假設(shè)F和G下有一個(gè)單調(diào)遞增的有界閉吸收集H={H(t)}t∈R,其中H(t)由(25)式給出,且有唯一的后項(xiàng)緊拉回吸引子A={A(t)}t∈R,其中

A(t)=ωX(H(t),t)=

(39)

證明由定理2.1和定理2.2可知定理1.1的條件(i)、(ii)滿足,故由定理1.1知定理2.3成立.

[1]CARABALLOT,CARVALHOAN,LANGAJA,etal.Existenceofpullbackattracttorsforpullbackasymptoticallycompactprocesses[J].NonlinearAnal,2010,72(3):1967-1976.

[2]WANGBX.Sufficientandnecessarycriteriaforexistenceofpullbackattractorsfornon-compactrandomdynamicalsystems[J].JDiffEqns,2012,253(5):1544-1583.

[3]LIYR,GUAH,LIJ.Existenceandcontinuityofbi-spatialrandomattractorsandapplicationtostochasticsemilinearLaplacianequations[J].JDiffEqns,2015,258(2):504-534.

[4]LIYR,YINJY.AmodifiedproofofpullbackattractorsinaSobolevspaceforstochasticFitzHugh-Nagumoequations[J].DisreteContinDynSyst,2016,21(4):1203-1223.

[5]CUIHY,LANGAJA,LIYR.Regularityandstructureofpullbackattractorsforreaction-diffusiontypesystemswithoutuniqueness[J].NonlinearAnal,2016,140:208-235.

[6]LIYR,WANGRH,YINJY.Bankwardcompactattratorsfornon-autonomousBenjsmin-Bona-Mahonyequationsonunboundedchannels[J].DiscreteContinDynSyst,2017,B22(7):2569-2586.

[8]CARVALHOAN,LANGAJA,ROBINSONJC.AttractorsforInfinite-dimensionalNon-autonomousDynamicalSystems[M].NewYork:Springer-Verlag,2013:182.

2010MSC:35K57; 35B41

(編輯 周 俊)

The Backward Compactness of Pullback Attractors for Nonautonomous Reaction-Diffusion Equations

SHE Lianbing1, WANG Renhai2

(1.DepartmentofMathematics,LiupanshuiNormalCollege,Liupanshui553004,Guizhou;2.SchoolofMathematicsandStatistics,SouthwestUniversity,Chongqing400715)

A sufficient condition for the existence of a unique and backward compact pullback attractor for a nonautonomous process defined on the Banach space is established. This result is applied to prove that the nonautonomous reaction-diffusion equation has a unique and backward compact pullback attractor under some relative weak assumptions.

nonautonomous dynamic systems; pullback attractor; backward compactness; nonautonomous reaction-diffusion equation

O117.8

A

1001-8395(2017)06-0797-05

10.3969/j.issn.1001-8395.2017.06.015

2016-11-15

國家自然科學(xué)基金(11571283)、貴州省教育廳自然科學(xué)基金(KY[2016]103和KY[2016]271)和貴州省科學(xué)技術(shù)基金(LP[2015]7612和LKLS[2013]14)

佘連兵(1981—),男,副教授,主要從事微分方程和無窮維動(dòng)力系統(tǒng)的研究,E-mail:shelianbing@163.com