雙向MIMO中繼系統中一種低復雜度的聯合信道估計方法

杜建和 花 妍 林和昀 田 沛

?

雙向MIMO中繼系統中一種低復雜度的聯合信道估計方法

杜建和*①花 妍①林和昀②田 沛①

①(中國傳媒大學信息工程學院 北京 100024)②(北京郵電大學信息與通信工程學院 北京 100876)

對于雙向多輸入多輸出(MIMO)中繼系統，如何在減少中繼負擔的情況下獲得精確的信道狀態信息(CSI)成為信道估計的一個難點。該文針對雙向MIMO中繼系統，提出一種低復雜度的聯合信道估計方法。所提方法在兩個用戶端同時發送正交信道訓練信號至中繼，中繼采用所設計的放大因子放大所接收的信號并轉發至兩個用戶。每個用戶對所接收的信號構造平行因子(PARAFAC)模型，并根據實際系統要求，分別設計了迭代和非迭代的兩種擬合算法對PARAFAC模型進行擬合，從而聯合估計出所有信道的CSI。所提信道估計方法無需在中繼處進行信道估計，減輕了中繼的負擔。與已有信道估計方法相比，所提方法設計靈活，采用的擬合算法具有較低的復雜度，而且在使用較少信道訓練信號的情況下具有較高的信道估計精度。

雙向MIMO中繼；低復雜度；信道狀態信息；平行因子

1 引言

當中繼系統與多輸入多輸出(Multiple-Input Multiple-Output, MIMO)技術相結合，能充分利用空間分集，進一步提高了系統的性能。目前，MIMO中繼系統已經引起了學術界和工業界的廣泛關 注[1,2]。大量關于MIMO中繼方面的研究工作都假設系統已知精確的信道狀態信息(Channel State Information, CSI)。然而在實際通信中，CSI是未知的，因此需要被估計。

針對MIMO中繼系統，文獻[3]提出了一種兩階段信道估計方法，該方法能在信宿端估計出信源到中繼和中繼到信宿的信道矩陣。文獻[4]提出了一種基于平行因子模型(PARAllel FACtor, PARAFAC)[5,6]的信道估計方法，該方法能聯合估計出兩跳信道矩陣。文獻[7]對文獻[4]中的交替最小二乘(Alternating Least-Squares, ALS)擬合算法進行優化和改進，降低了計算復雜度。文獻[8]針對上行多用戶MIMO系統，利用LM(Levenberg- Marquardt)擬合算法快速收斂的特性，提高了信道估計的效率。

文獻[3,4,7,8]都是針對于單向MIMO中繼系統，與單向MIMO中繼系統相比，雙向MIMO中繼系統具有更高的頻譜效率[9]。然而，雙向MIMO中繼系統的信道估計問題也相對復雜。針對雙向MIMO中繼系統，文獻[10]提出了一種級聯信道估計方法。文獻[11]進一步將文獻[4]中的方法擴展到了雙向MIMO中繼系統，在用戶端估計出兩跳信道的CSI。文獻[12]在文獻[3]的基礎上，針對雙向MIMO中繼系統提出了一種新的兩階段信道估計方法。然而該方法的第1跳信道矩陣估計精度仍然依賴于第2跳信道矩陣的估計精度，而且需要兩次在中繼處對發送功率進行優化才能獲得較好的信道估計性能，具有較高的計算復雜度。

本文針對雙向MIMO中繼系統，提出了一種低復雜度的聯合信道估計方法。所提方法在兩個用戶端設計相互正交的信道訓練信號進行發送，中繼采用不同的放大因子對接收的信號進行放大轉發，在用戶端構造PARAFAC模型，利用迭代的P-ALS- LS(PARAFAC-ALS with linear search)和非迭代的P-KRF(PARAFAC with Khatri-Rao Factorization) 擬合算法能估計出每一跳的信道矩陣。

本文主要創新點如下：

(1)所提方法無需在中繼處進行信道估計，在用戶端就能估計出所有信道的CSI；而且所提信道估計方法設計靈活，可根據系統要求考慮信道估計精度和估計效率的折中。

(2)所提方法設計了P-ALS-LS和P-KRF算法對所構造的PARAFAC模型進行擬合。與文獻[11]提出的迭代TP-ALS (Traditional PARAFAC with ALS)算法相比，所提算法具有較低的復雜度，特別是P-KRF算法；此外，還可以根據系統參數來選擇合適的擬合算法。

(3)在較小的信道訓練數目條件下，所提信道估計方法比文獻[11]的方法具有更高的信道估計精度。與兩階段信道估計方法[12]相比，所提信道估計方法具有更好的第2跳信道估計精度。

2 系統模型

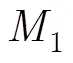
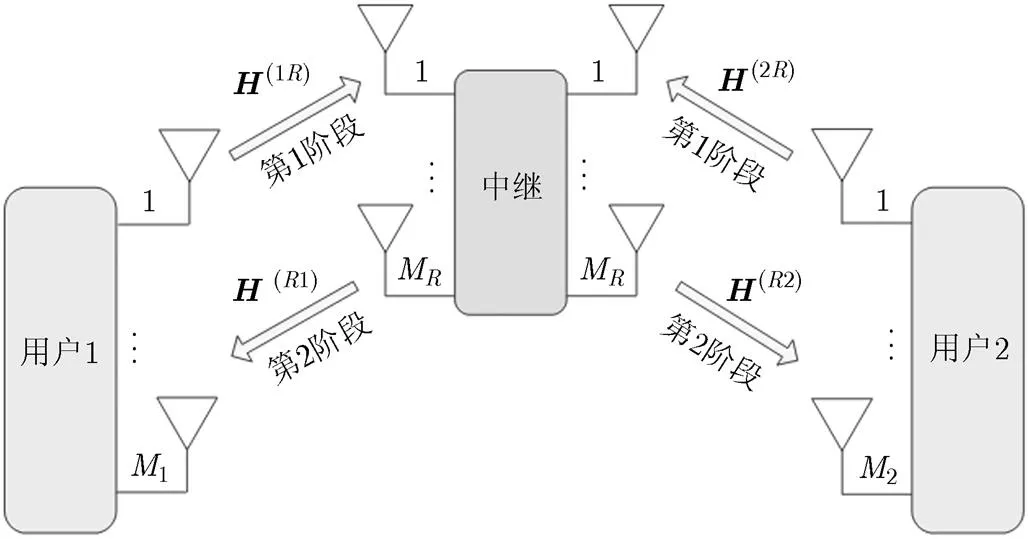
圖1 雙向MIMO中繼通信系統

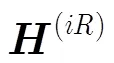
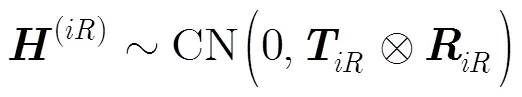
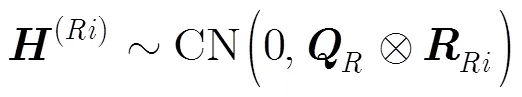
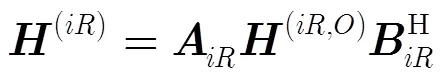
3 所提信道估計方法

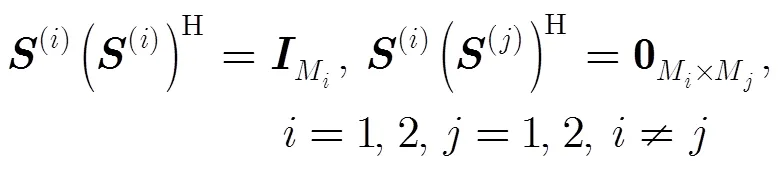
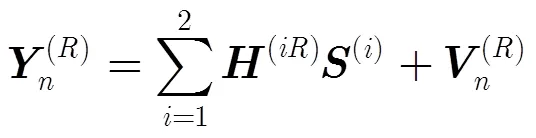
3.1 PARAFAC模型的構造

由式(7)可得

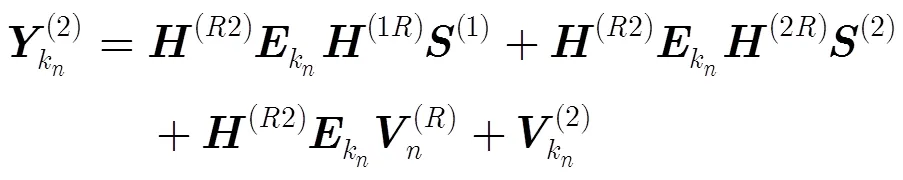
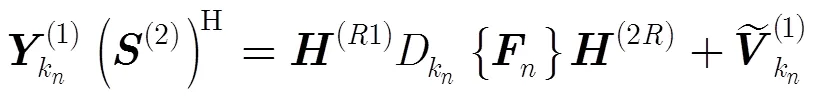
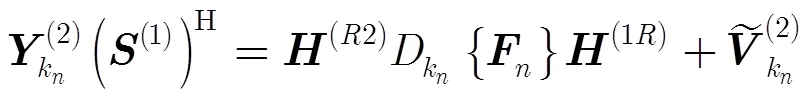
其中，

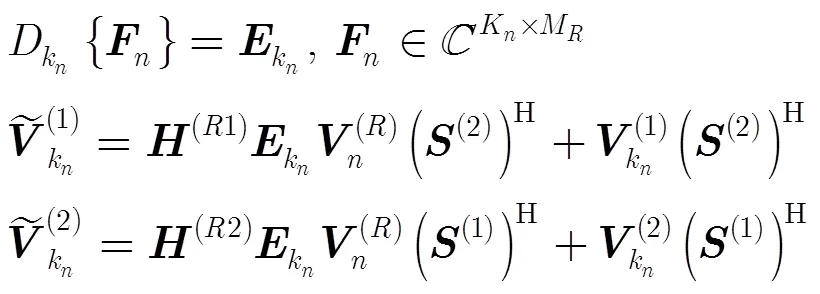
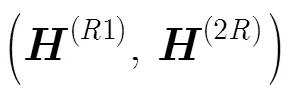
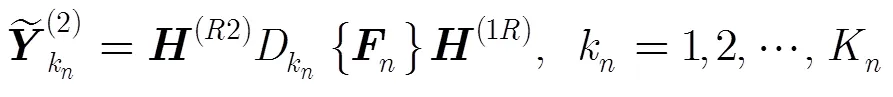
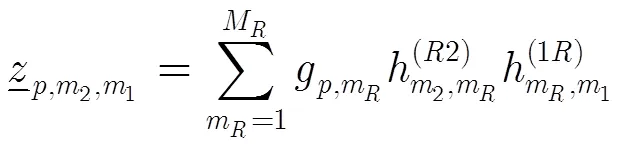
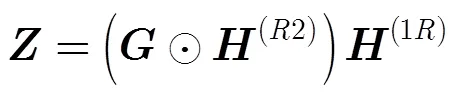
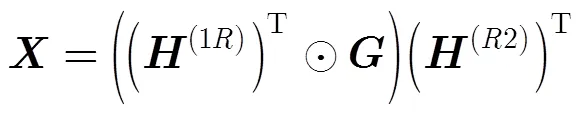
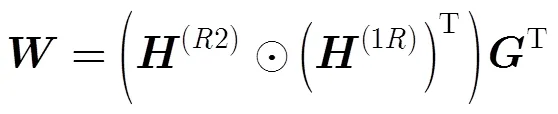
3.2 分解唯一性

根據PARAFAC模型的分解唯一性定理[6]，所構模型式(13)的唯一性條件為

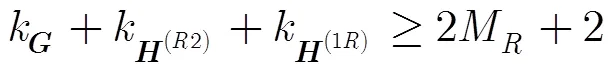
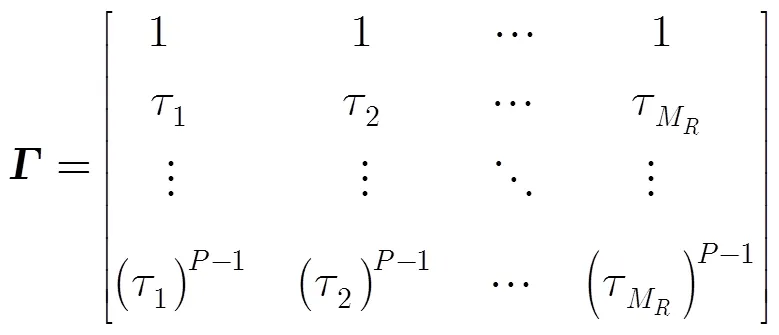
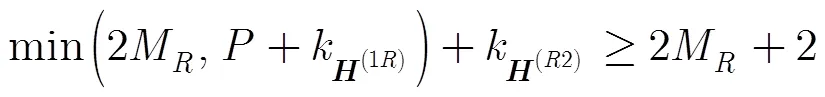
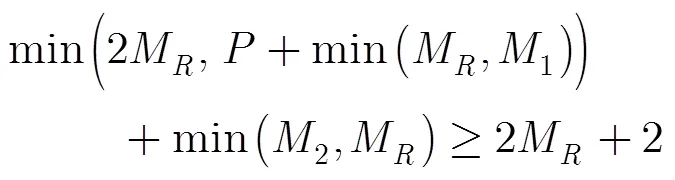
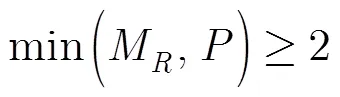
4 擬合算法的設計

為了快速而精確地估計出每一跳的信道矩陣，本文設計了兩種有效的擬合算法來擬合所構造的PARAFAC模型，即P-ALS-LS和P-KRF擬合算法。

4.1 P-ALS-LS算法

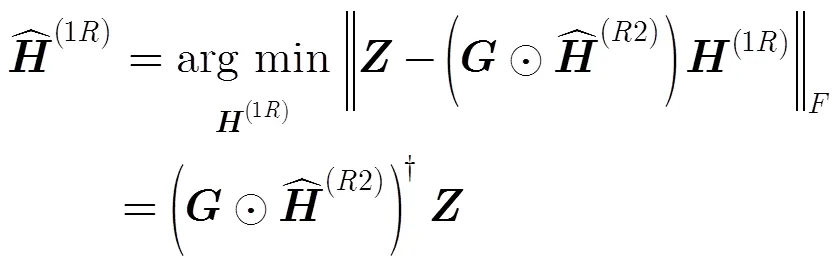
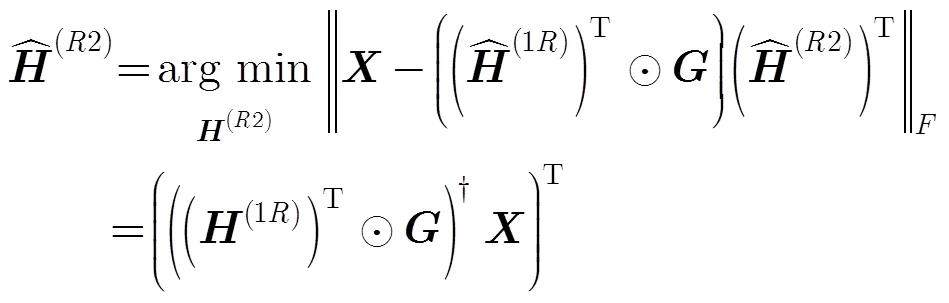
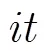
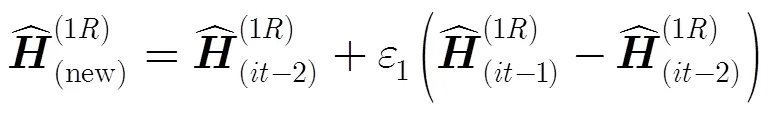
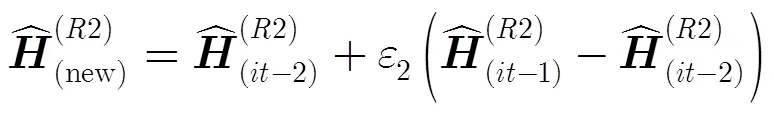
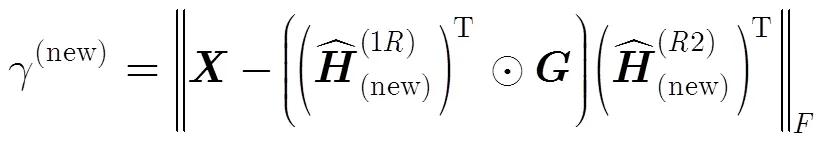
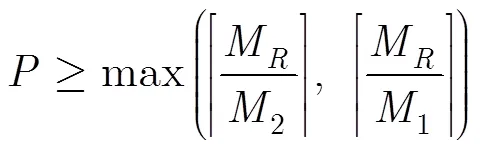
4.2 P-KRF算法

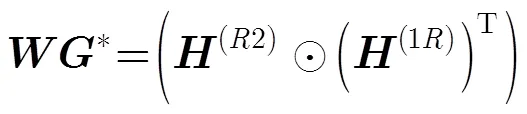
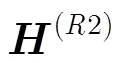
所提P-KRF算法的具體實現步驟如下：

5 仿真與分析

表1 不同算法的計算復雜度比較

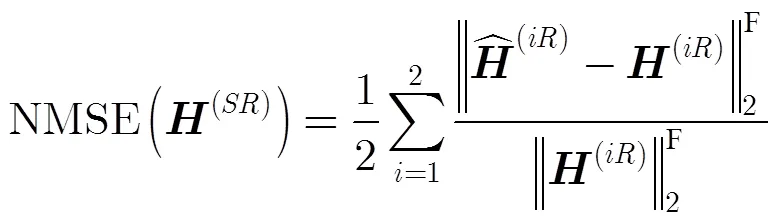
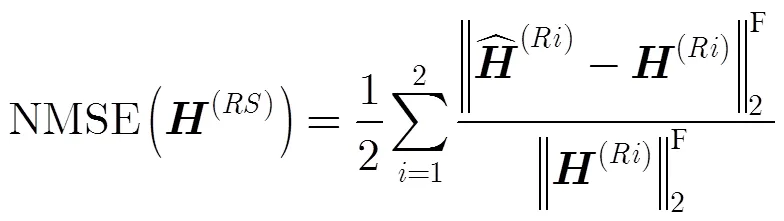
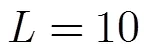
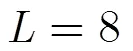
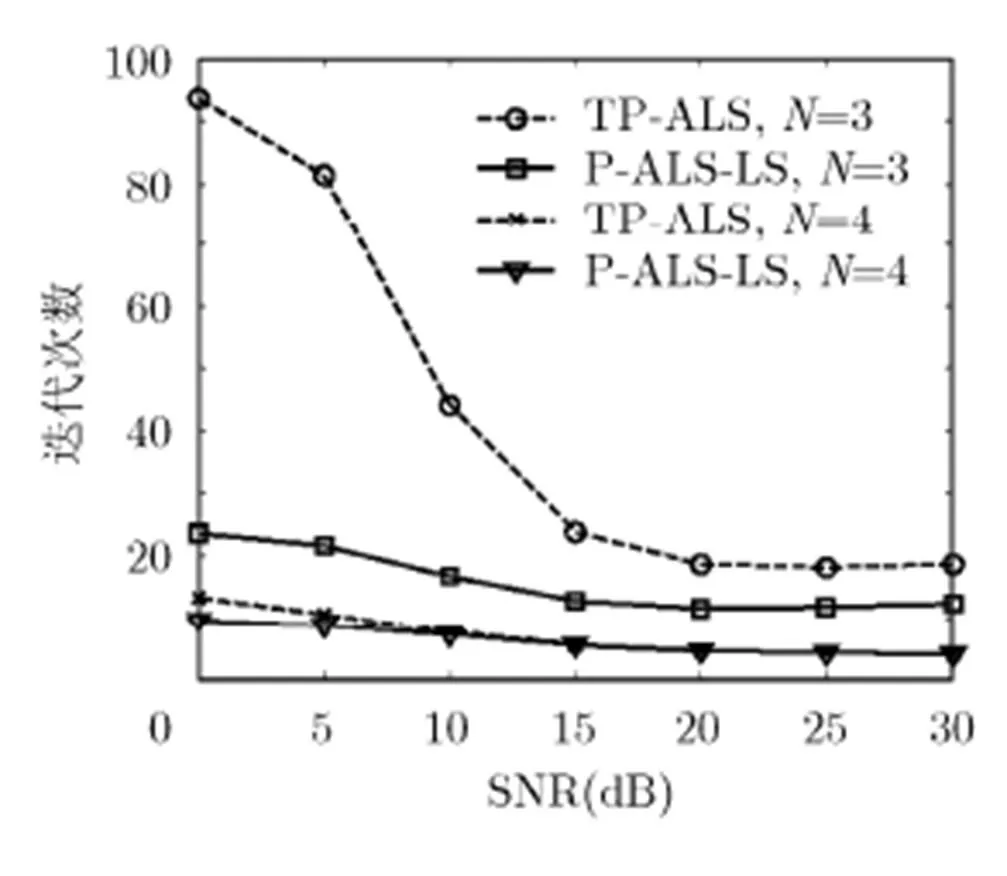
圖2 TP-ALS和P-ALS-LS算法達到收斂所需的迭代次數

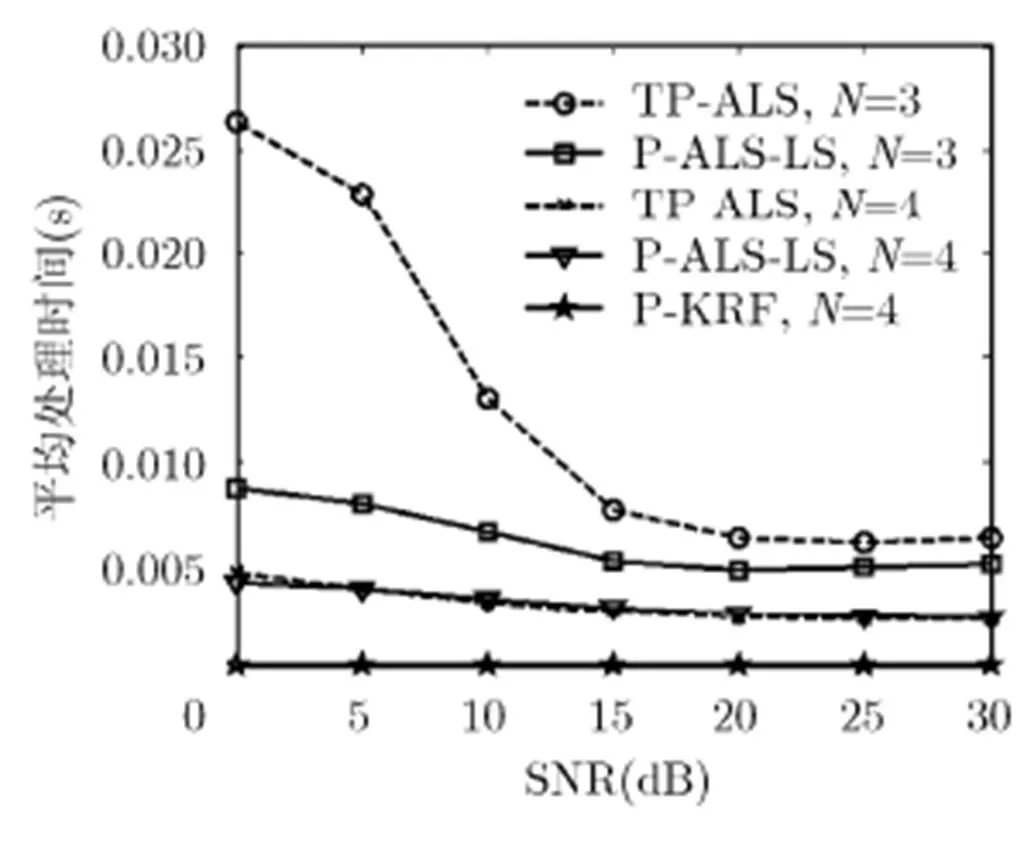
圖3 TP-ALS, P-ALS-LS和P-KRF算法所需的平均處理時間

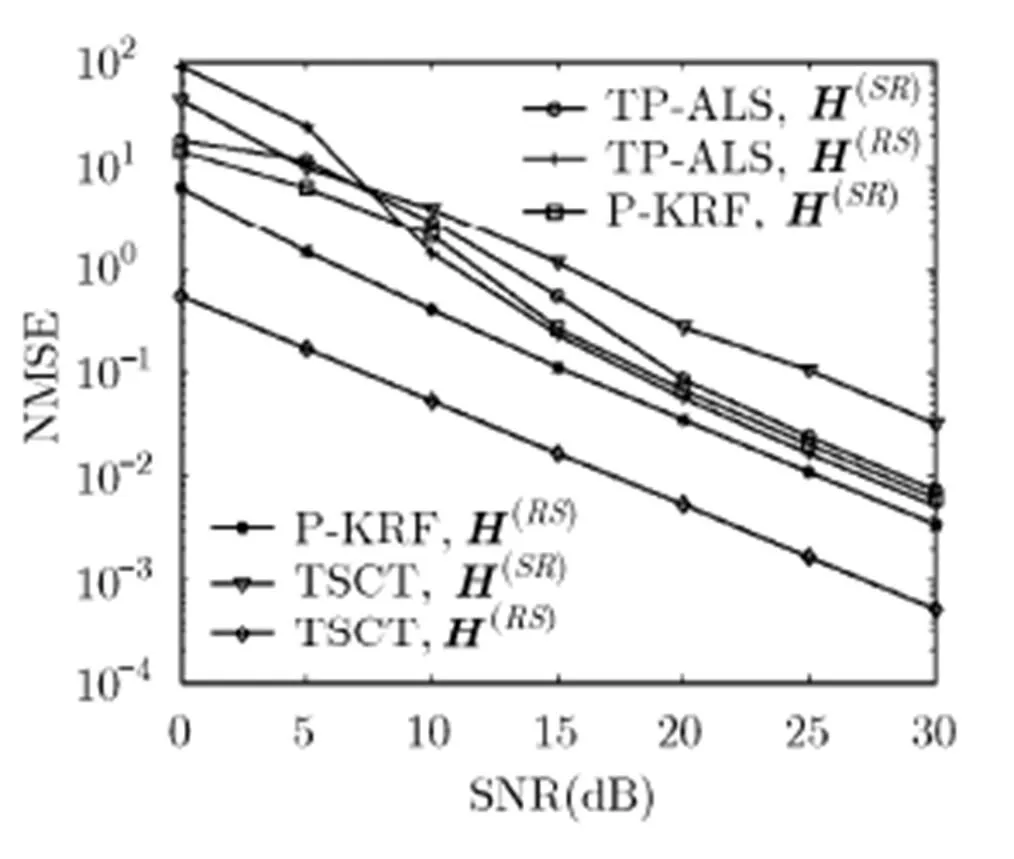
圖4 TP-ALS算法、所提P-KRF算法和TSCT算法的NMSE性能比較

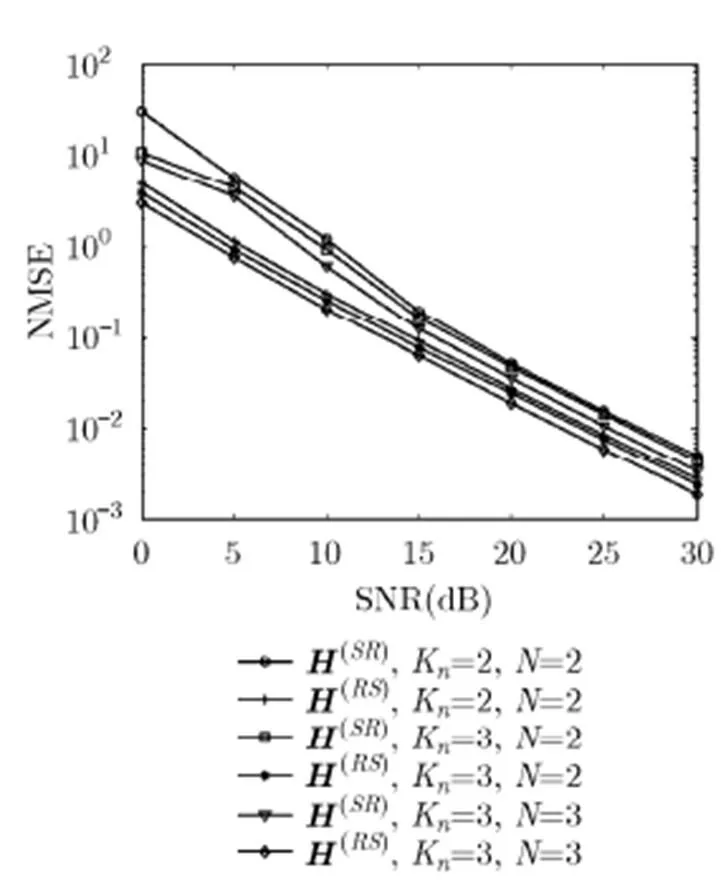
圖5 不同系統參數N與下，所提算法的NMSE性能

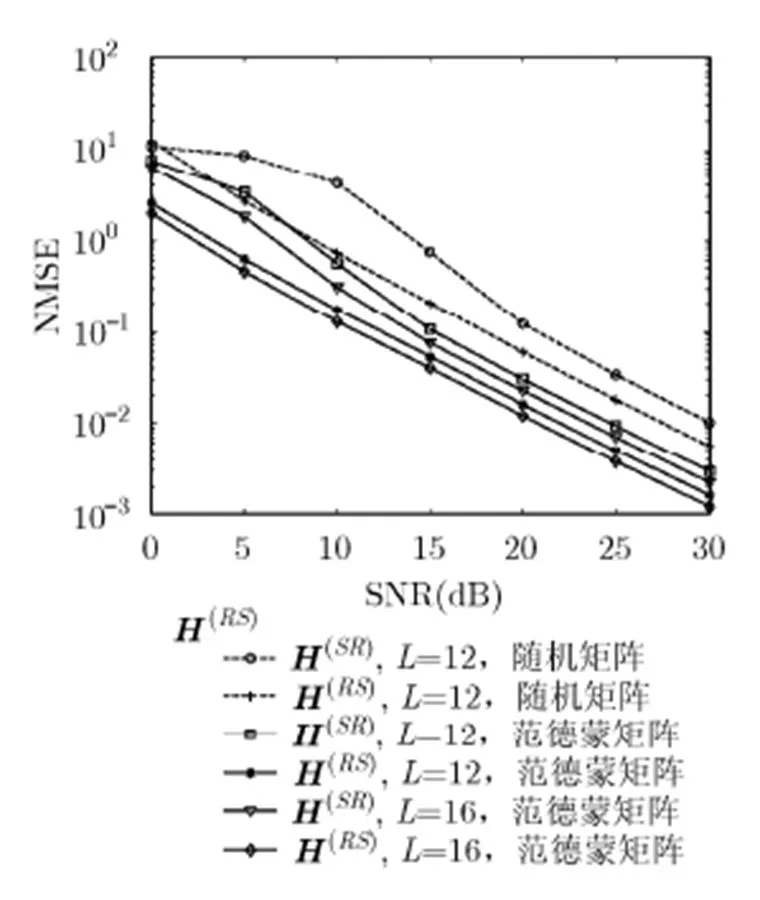
圖6 放大矩陣和訓練信號長度對所提算法性能的影響

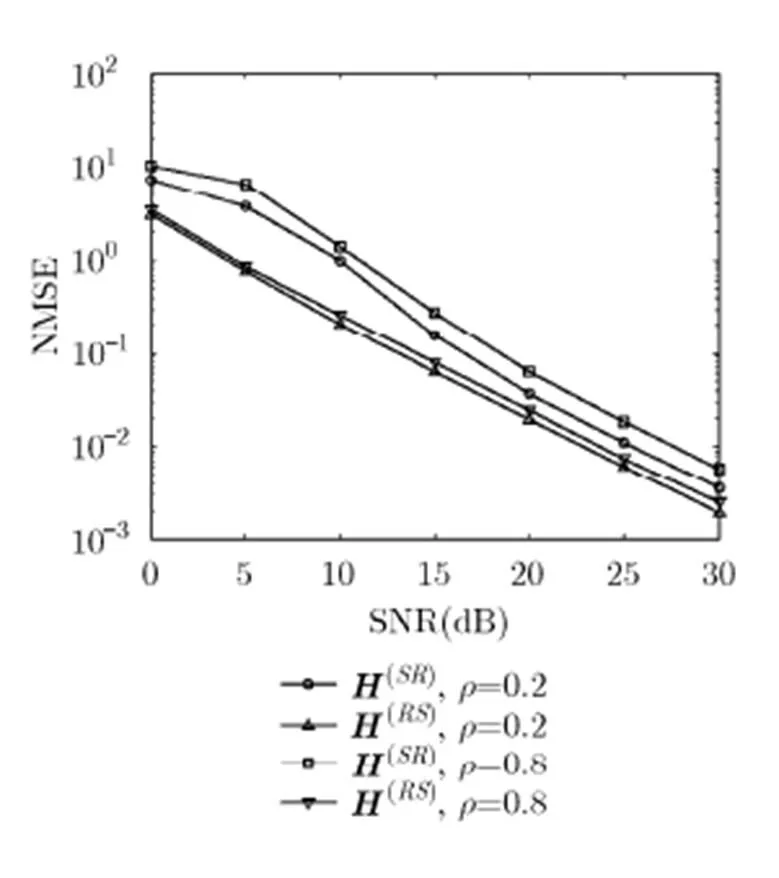
圖7 信道相關系數對所提算法性能的影響

6 結束語

本文針對雙向MIMO中繼系統，提出了一種低復雜度的信道估計方法。所提方法能在用戶端估計出所有信道的CSI。本文詳細闡述了所提信道估計方法的建模，唯一性條件和擬合算法的設計。與已有信道估計方法相比，所提方法具有較高的信道估計精度，而且可以根據系統要求選擇相應低復雜度的擬合算法，仿真驗證了所提信道估計方法的性能。下一步的研究工作將針對雙向MIMO中繼系統，考慮聯合信道與符號估計方案，即在假設CSI未知的條件下，無需發送信道訓練信號，僅僅利用發送的有用符號和雙向中繼信道互易性特點，通過構造高維的PARAFAC模型或TUCKER模型，設計相應的擬合算法在用戶端對信道和符號進行聯合估計。

[1] NOSRATINIA A, HUNTER T E, and HEDAYAT A. Cooperative communication in wireless networks[J]., 2004, 42(10): 74-80. doi: 10.1109 /MCOM.2004.1341264.

[2] JIN X and KIM Y H. The approximate capacity of the MIMO relay channel[J]., 2017, 63(2): 1167-1176. doi: 10.1109/TIT.2016.2632625.

[3] KONG Ting and HUA Yingbo. Optimal design of source and relay pilots for MIMO relay channel estimation[J]., 2011, 59(9): 4438-4446. doi: 10.1109/TSP.2011.2158429.

[4] RONG Yue and KHANDAKER M R A. Channel estimation of dual-hop MIMO relay systems using parallel factor analysis[C]. 2011 IEEE 17th Asia-Pacific Conference on Communications (APCC), Sabah, Malaysia, 2011: 278-283. doi: 10.1109/APCC.2011.6152819.

[5] SIDIROPOULOS N D, BRO R, and GIANNAKIS G B. Parallel factor analysis in sensor array processing[J]., 2000, 48(8): 2377-2388. doi: 10.1109/78.852018.

[6] SIDIROPOULOS N D, DE Lathauwer L, FU Xiao,. Tensor Decomposition for Signal Processing and Machine Learning[J]., 2017, 65(13): 3551-3582. doi: 10.1109/TSP.2017.2690524.

[7] DU Jianhe, YUAN Chaowei, and ZHANG Jinbo. Low complexity PARAFAC-based channel estimation for non- regenerative MIMO relay systems[J]., 2014, 8(12): 2193-2199. doi: 10.1049/iet-com.2013.1155.

[8] 林和昀, 袁超偉, 杜建和. 一種多用戶上行放大轉發中繼系統中快速收斂的信道估計方法[J]. 物理學報, 2016, 65(21): 35-43. doi: 10.7498/aps.65.210201.

LIN Heyun, YUAN Chaowei, and DU Jianhe. A fast algorithm with convergence for channel estimation in multi- user uplink amplify-and-forward relay system[J]., 2016, 65(21): 35-43. doi: 10.7498/aps.65. 210201.

[9] SANGUINETTI L, D,AMICO A A, and RONG Yue. A tutorial on the optimization of amplify-and-forward MIMO relay systems[J]., 2012, 30(8): 1331-1346. doi: 10.1109/JSAC. 2012.120904.

[10] FANG Zhaoxi, JIONG Shi, and SHAN Hangguan. Comparison of channel estimation schemes for MIMO two-way relaying systems[C]. 2011 IEEE Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC), 2011, 1: 719-722. doi: 10.1109/ CSQRWC.2011.6037053.

[11] RONG Yue, KHANDAKER M R A, and YONG Xiang. Channel estimation of dual-hop MIMO relay system via parallel factor analysis[J]., 2012, 11(6): 2224-2233. doi: 10.1109/TWC. 2012.032712.111251.

[12] CHIONG C W R, RONG Yue, and YONG Xiang. Channel training algorithms for two-way MIMO relay systems[J]., 2013, 61(16): 3988-3998. doi: 10.1109/TSP.2013.2265223.

[13] GHASEMI-GOOJANI S, KARIMI-BIDHENDI S, and BEHROOZI H. On the capacity region of asymmetric gaussian two-way line channel[J]., 2016, 64(9): 3669-3682. doi: 10.1109/ TCOMM.2016.2597852.

[14] 王林, 芮國勝, 張海波. 雙向中繼系統用戶聯合預編碼與檢測算法研究[J]. 電子與信息學報, 2015, 37(7): 1550-1555. doi: 10.11999/JEIT141455.

WANG Lin, RUI Guosheng, and ZHANG Haibo. Research on users joint precoding and detection in two-way relay systems[J].&, 2015, 37(7): 1550-1555. doi: 10.11999/JEIT141455.

[15] S?RENSEN M and DE LATHAUWER L. Blind signal separation via tensor decomposition with Vandermonde factor: Canonical polyadic decomposition[J]., 2013, 61(22): 5507-5519. doi: 10.1109/TSP. 2013.2276416.

[16] FAVIER G, FERNANDES C A R, and DE ALMEIDA A L F. Nested Tucker tensor decomposition with application to MIMO relay systems using tensor space-time coding (TSTC) [J]., 2016, 128: 318-331. doi: 10.1016/ j.sigpro.2016.04.009.

[17] RAJIH M, COMON P, and HARSHMAN R A. Enhanced line search: A novel method to accelerate PARAFAC[J]., 2008, 30(3): 1128-1147. doi: 10.1137/06065577.

[18] DU Jianhe, YUAN Chaowei, HU Zhongwei,. A novel tensor-based receiver for joint symbol and channel estimation in two-hop cooperative MIMO relay systems[J]., 2015, 19(11): 1961-1964. doi: 10. 1109/LCOMM.2015.2473172.

[19] XIMENES L R, FAVIER G, and DE ALMEIDA A L F. Closed-form semi-blind receiver for MIMO relay systems using double Khatri-Rao space-time coding[J]., 2016, 23(3): 316-320. doi: 10.1109/LSP. 2016.2518699.

杜建和： 男，1984年生，博士，講師，主要研究方向為中繼通信、信道估計與多維信號處理技術.

花 妍： 女，1988年生，博士，講師，主要研究方向為信號分析與處理技術.

林和昀： 男，1985年生，博士生，研究方向為多天線與信道估計技術.

田 沛： 男，1970年生，博士，教授，主要研究方向為通信與信息網絡技術.

A Low-complexity Algorithm for Joint Channel Estimation inTwo-way MIMO Relay Communication Systems

DU Jianhe①HUA Yan①LIN Heyun②TIAN Pei①

①(,,100024,)②(,,100876,)

For two-way Multiple-Input Multiple-Output (MIMO) relay communication systems, the main challenge is to get full knowledge of all channel matrices with minimal cost of signal handling at the relay node. In this paper, a low-complexity joint channel estimation scheme for two-way MIMO relay communication systems is proposed. Both users transmit orthogonal channel training signals to the relay node simultaneously. Then the relay amplifies the received signals by using designed amplification factors, and forwards the amplified signals to both users. The received signals at each user is formulated as a PARAllel FACtor (PARAFAC) model, and then the iterative and non-iterative fitting algorithms are derived to estimate the Channel State Information (CSI) knowledge of all links involved. Compared with existing schemes, the proposed scheme has the advantages of design flexibility and low complexity, and has higher estimation accuracy with a few number of channel training signals.

Two-way MIMO relay; Low-complexity; Channel State Information (CSI); Parallel factor

TN929.53

A

1009-5896(2017)12-2976-07

10.11999/JEIT170463

2017-05-16；

2017-09-16；

2017-11-02

通信作者：杜建和 dujianhe1@163.com

國家自然科學基金(61601414, 61561037)，國家高技術研究發展計劃(2015AA01A705, 2014AA01A701)

: The National Natural Science Foundation of China (61601414, 61561037), The National High Technology Research and Development Program of China (2015AA01A705, 2014AA01A701)