基于Fourier-Mellin和Delaunay三角網的GBSAR影像配準研究

岳 順，岳建平，邱山鳴，汪學琴

(1.河海大學 地球科學與工程學院，江蘇 南京 210098；2.水能資源利用關鍵技術湖南省重點實驗室，湖南 長沙 410014)

?

基于Fourier-Mellin和Delaunay三角網的GBSAR影像配準研究

岳 順1，岳建平1，邱山鳴2，汪學琴1

(1.河海大學 地球科學與工程學院，江蘇 南京 210098；2.水能資源利用關鍵技術湖南省重點實驗室，湖南 長沙 410014)

GBSAR的高精度測量需要準確的干涉相位來保證，因此影像間的配準尤為重要。針對傳統GBSAR影像配準方法沒有充分考慮到同名點的幾何分布和空間結構關系的問題，文中基于Fourier-Mellin和Delaunay三角網的特性，對GBSAR影像數據進行粗配準和精配準。結合GBSAR影像實例數據，并對配準結果的相干系數圖進行統計分析，結果表明此方法可提高影像配準的精度，為GBSAR影像數據的后續處理提供較好參考。

Fourier-Mellin; Delaunay三角網；GBSAR；配準;相干系數

隨著衛星微波遙感技術的不斷發展，地基合成孔徑雷達(Ground Based Synthetic Aperture Radar, GBSAR)技術也越來越受到研究者的重視[1-2]。GBSAR的原理與星載SAR原理類似，但比星載SAR具有更高的時間分辨率和空間分辨率，且攜帶方便、易操作，可以達到亞毫米級的監測精度，已被廣泛應用于變形監測中[3-4]。GBSAR與傳統的GPS、全站儀等測量技術相比，具有空間連續覆蓋的優點，可以對大型建筑物進行動態監測。雖然GBSAR在變形監測方面具有較大的優勢，但是GBSAR也有自身的缺陷。GBSAR系統在長期監測的過程中，會出現監測平臺不穩定、時間和噪聲去相關等問題，如果不及時解決這些問題，會對所獲取的GBSAR影像造成部分的偏移和縮放，降低影像之間的相干性，進而使監測結果的精度下降。為解決上述問題，必須對GBSAR影像進行精確的配準。GBSAR影像的高精度配準是GBSAR影像數據處理中的重點和難點，同時也是提高GBSAR系統監測精度的關鍵步驟[5]。目前，GBSAR影像配準的方法有很多種，例如：最大干涉頻譜法、灰度信息法、變化域法等。但這些方法大部分是建立在同名點的基礎上，運算效率低，沒有考慮到同名點之間的幾何分布和空間結構關系，導致GBSAR配準結果存在較大的偏差[6-7]。如何結合全局的特征匹配與局部的特征間的分布信息成為提高配準精度的一種思路[8-11]。Delaunay三角網技術在地質學、測繪學、物理學和化學及計算幾何學等眾多領域都有非常廣泛的應用。本文結合Fourier-Mellin和Delaunay三角網的特性，對GBSAR影像進行粗配準和精配準，并用實測GBSAR數據對該方法進行驗證，得到較好的結果。

1 基于Fourier-Mellin和Delaunay三角網在GBSAR數據配準的原理

影像的精確配準對GBSAR高精度的形變測量十分重要[12]。在配準過程中，首先在監測區域內獲得的GBSAR影像中選取對應的主輔影像。本文先用Fourier-Mellin對主輔影像進行粗配準，再利用Delaunay三角網進行精確配準，最終得到高精度的GBSAR影像配準結果。

1.1 基于Fourier-Mellin的GBSAR影像粗配準

Fourier-Mellin是在GBSAR影像頻域內計算主輔影像之間的平移量、旋轉角度和縮放因子，從而實現影像間的粗配準[13]。其配準理論如下：

設I1(x,y)，I2(x,y)分別為GBSAR兩幅影像。其中I1(x,y)為主影像，I2(x,y)為輔影像。I1(x,y)，I2(x,y)的Fourier變化為F1(u,v)和F2(u,v)，則

(1)

其互功率譜為

(2)

Corr(u,v)稱為相位相關函數，其中

(3)

(4)

(5)

對其進行Fourier變化得

(6)

設F1(u,v)和F2(u,v)的幅度譜分別為M(u,v)和S(u,v)，則

(7)

從式(7)可以看出，頻譜的幅度只與其旋轉角θ0和縮放因子σ有關，而與影像間的平移量(x0,y0)無關，因此旋轉角θ0、縮放因子σ和平移量(x0,y0)可以分開計算。首先需要在影像頻率域計算出旋轉角θ0和縮放因子σ，然后將影像幅度譜中的(u,v)變化到極坐標(ρ,θ)下。它們的關系為

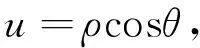
(8)

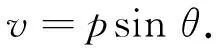
(9)

由式(7)可得

(10)

將式(10)變化到對數—極坐標系下得

(11)

取λ=logρ,α=logσ，則式(11)變為

(12)

在主輔影像配準過程中，由于雷達波速寬度不會因為軌道發生變化，因此主輔影像之間的縮放因子σ=1。則式(12)可寫成

(13)

1.2 基于Delaunay三角網的GBSAR影像精配準

本文采用Fourier-Mellin算法對GBSAR主輔影像進行粗配準之后，得到兩影像間的平移量(x0,y0)和旋轉角度θ0，然后根據所得參數對輔影像進行旋轉平移變化，最終得到粗配準后的影像。接下來利用Delaunay三角網對粗配準之后的影像進行精配準[14]，進行Delaunay三角網精配準的步驟如下：

1)利用Moravec算法提取GBSAR主輔影像同名候選點；

2)分別利用主輔影像上的同名點集構建Delaunay三角網；

3)以三角形為單位分別計算主輔影像的Delaunay三角網的相似度，得到主輔圖像的相似度矩陣；

4)在計算得到的相似度矩陣中搜索相似度大于閾值的三角形對，并把該三角對列為候選匹配三角形對；

5)分別選取候選匹配三角形的3條邊向外延伸的三角形，用候匹配三角形的3個頂點為中心組成3個共點線束，判斷是否正確匹配該候匹配三角形。若正確匹配，則分別在各三角網中保留候匹配三角形的頂點。若不是正確匹配，則分別從兩個三角網中刪除候匹配三角形的頂點，如此反復直到處理完所有的候選匹配三角形對，最終使主輔像上的Delaunay三角網完全相同，則組成該Delaunay三角網的離散點與其對應點即為所需的正確匹配點對集合；

6) 用得到的正確匹配點經仿射變換后計算主輔像的空間變換參數，實現主輔影像的精確配準。

2 GBSAR數據配準實驗分析

本文基于上述算法原理，選取觀測時間分別為09:40和15:08的兩幅GBSAR影像，觀測地點位于隔河巖大壩附近，以09:40觀測數據為主影像，15:08的觀測數據為輔影像，利用實測GBSAR影像數據對本文的配準算法進行驗證。為了驗證本算法的精確性，本文同時采用最大干涉頻譜法和Delaunay三角網離散點配準算法，利用多項式配準模型對以上兩幅GBSAR影像進行配準。圖1、圖2為GBSAR系統在不同時間獲取的同一目標區域成像幅度圖像，主輔圖像大小均為700像素×130像素。

圖1 主影像幅度圖

相干系數圖是對GBSAR影像配準結果最直接和有效的檢驗。圖3～圖5分別是基于最大干涉頻譜法、Delaunay三角網離散點、Fourier-Mellin和Delaunay三角網3種配準方法配準后相干系數圖，并對其進行直方圖統計，結果如圖6～圖8所示。

圖3 最大干涉頻譜法配準后的相干系數圖

圖4 Delaunay三角網離散點配準后相干系數圖

圖5 Fourier-Mellinto Delaunay三角網配準后相干系數圖

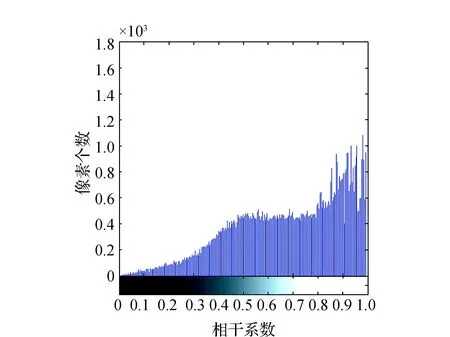
圖6 最大干涉頻譜法配準后的相干系數統計圖

圖7 Delaunay三角網離散點配準后的相干系數統計圖

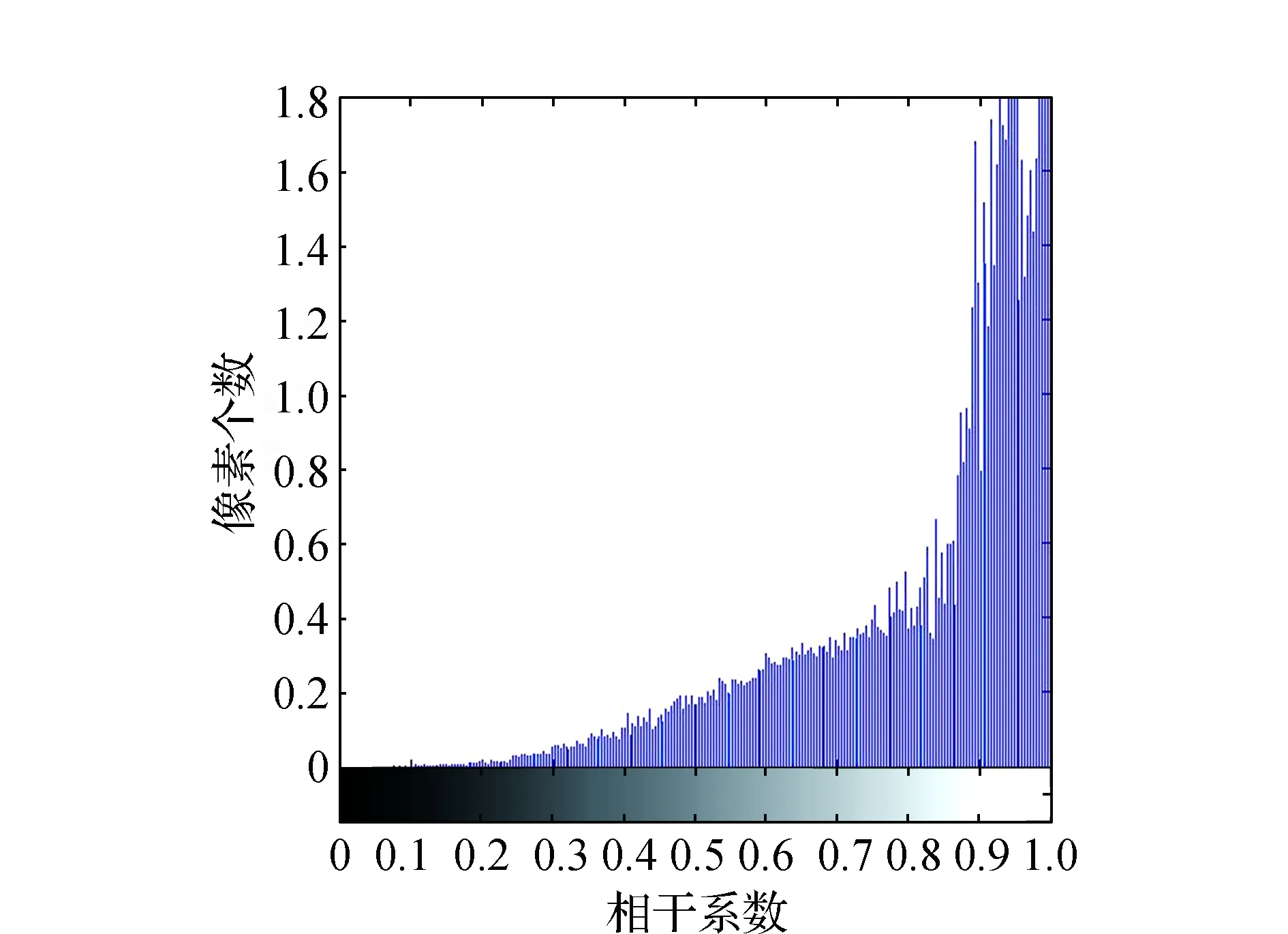
圖8 Fourier-Mellin和Delaunay三角網配準后相干系數統計圖

從圖3～圖5對比可以看出，亮度值高處表示相干性高，干涉質量好。通過最大干涉頻譜法、Delaunay三角網離散點、Fourier-Mellin和Delaunay三角網配準后影像對的相干性都有較大的提高，但是從圖6～圖8可以看出，最大干涉頻譜法和Delaunay三角網離散點配準后的相干系數幾乎平均分布在[0.5,1]內，而Fourier-Mellin和Delaunay三角網配準后的相干系數集中分布在[0.8,1]內，說明基于Fourier-Mellin變換和Delaunay三角網相結合的配準算法在GBSAR影像配準中具有較好的實用性。

3 結束語

為解決長時間觀測GBSAR系統不穩定產生的影像偏差，同時考慮到主輔影像配準過程中影像同名點的幾何分布和空間結構關系，針對傳統GBSAR影像配準方法的不足，本文采用Fourier-Mellin對主輔影像進行粗配準，采用Delaunay三角網實現主輔影像的精配準，通過相干系數圖可以看出，Fourier-Mellin和Delaunay三角網相結合的算法提高影像間的相干系數和配準精度，確保GBSAR干涉相位的準確性，為GBSAR的進一步處理提供較好的保障。

[1] 岳建平,曾寶慶,郭騰龍,等. GB-Radar與測量機器人數據融合方法研究[J]. 測繪通報,2014(10):33-35.

[2] 張祥. 地基SFCW SAR差分干涉測量技術研究[D].長沙：國防科學技術大學,2011.

[3] 熊博蒞.SAR圖像配準及變化檢測技術研究[D].長沙：國防科學技術大學,2012.

[4] 陶秋香,劉國林.永久散射體差分干涉測量技術中SAR影像精配準的一種新方法[J]. 測繪學報,2012，41(1):69-73.

[5] 張宗營. SAR影像配準方法研究[D].青島：山東科技大學,2010.

[6] 岳春宇,江萬壽. 幾何約束和改進SIFT的SAR影像和光學影像自動配準方法[J]. 測繪學報,2012，41(4):570-576.

[7] 程海琴,陳強,劉國祥,等. 基于相干曲面移動擬合的SAR影像高精度配準方法[J]. 測繪科學,2013(5):137-140.

[8] 王青松,瞿繼雙,黃海風,等. 聯合實、復相關函數的干涉SAR圖像配準方法[J]. 測繪學報,2012，41(4):563-569.

[9] 王慶,曾琪明,焦健,等.基于DEM和查找表的高分辨率機載SAR圖像正射校正[J]. 測繪通報,2013(11):10-13.

[10] 楊海蘭,張利恒,韋春桃. 喀斯特地貌SAR影像多級配準方法[J]. 測繪科學,2015，40(1):72-76.

[11] 吳琴霞,梁興東,李焱磊,等. 殘余運動誤差對機載多波段SAR圖像配準的影響分析[J]. 雷達學報,2015，40(2):209-216.

[12] 蘇晨. 地基合成孔徑雷達變形監測技術研究[D].重慶：重慶大學,2014.

[13] 石曉進,張云華. 基于Fourier-Mellin變換和相干系數法的重復軌道干涉SAR圖像配準新方法[J]. 電子與信息學報,2009(4):803-807.

[14] 馬靈霞,鄒同元,徐京. 利用自動匹配與三角剖分進行遙感圖像幾何精校正[J].遙感學報,2011(5):927-939.

[責任編輯：張德福]

Research on the registration of GBSAR images based on Fourier-Mellin and Delaunay triangulation

Yue Shun1, Yue Jianping1, Qiu Shanming2, Wang Xueqin1

(1. School of Earth Science and Engineering of Hohai University, Nanjing 210098,China; 2.Hunan Provincial Key Laboratory of Key Technology on Hydropower Development, Changsha 410014,China)

The accurate interferometry phase can ensure the precision of GBSAR measurement. Therefore, the registration between images is particularly important. The traditional registration methods of GBSAR images do not fully take into account the geometric distribution and spatial structure relations of the same name points. This paper deals with GBSAR images by coarse registration and fine registration, based on the characteristics of Fourier-Mellin and Delaunay triangulation. Combined with GBSAR images, it makes a statistical analysis of the coherence graph factor of registration results. The results indicate that this method can improve the accuracy of images registration to a greater extent and provide a good reference for subsequent processing of GBSAR images.

Fourier-Mellin; Delaunay triangulation; GBSAR; registration;coherence factor

10.19349/j.cnki.issn1006-7949.2017.02.004

2015-09-11

國家自然科學基金資助項目(41174002)；水能資源利用關鍵技術湖南省重點實驗室開放研究基金項目(PKLHD201311)作者簡介：岳 順(1991-)，男，碩士.

TP79

A

1006-7949(2017)02-0014-04

引用著錄：岳順，岳建平，邱山鳴，等.基于Fourier-Mellin和Delaunay三角網的GBSAR影像配準研究[J].測繪工程，2017，26(1)：14-17.