基于粒子群算法的組合模型在變形分析中的應用

王顯鵬，黃聲享，李冠青

(1.廣州市增城區國土資源和規劃局,廣東 廣州 511300；2.武漢大學 測繪學院,湖北 武漢 430079)

?

基于粒子群算法的組合模型在變形分析中的應用

王顯鵬1,2，黃聲享2，李冠青2

(1.廣州市增城區國土資源和規劃局,廣東 廣州 511300；2.武漢大學 測繪學院,湖北 武漢 430079)

在構建并聯組合模型進行變形預測時，單項模型權值的確定是個關鍵問題。為了提高變形預測的精度，以基坑監測數據為例，采用GM(1,1)模型與ARMA模型進行組合，在擬合誤差平方和最小的準則下，使用粒子群算法求解兩單項模型的最優權值，進而構建并聯組合模型進行變形預測。結果表明，該方法融合各單項模型的優勢，可以提高預測精度，避免求解線性規劃問題，具有較好的實用性。

粒子群算法；GM(1,1)模型；ARMA模型；組合模型；變形分析

基坑監測可以及時地了解工程狀態，為決策者提供事實依據，對確保工程安全具有十分重要的意義。由于受到多種因素的影響[1-2]，使用單一預測模型進行變形分析往往具有一定的局限性，GM(1,1)模型和ARMA模型作為變形預測中常用的兩種模型，兩者各有優點和不足。將兩種方法進行結合構建組合模型，發揮兩者的優點，進一步挖掘數據信息，可以有效地降低預測過程中隨機因素的影響，提高預測精度[3-4]。

本文簡要介紹灰色GM(1,1)模型、ARMA模型和粒子群算法的基本原理，分別運用這兩種單項模型對觀測序列進行預測，得到相應的模擬值及殘差序列，然后在擬合誤差的平方和最小的準則下，使用粒子群尋找單項模型的最優權值，以此構建組合模型。

1 原理簡介

1.1 GM(1,1)模型

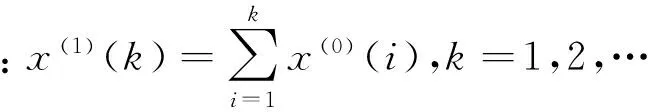
對序列x(1)建立一階微分方程

(2)

式中：a為發展系數;u稱為灰色作用量。用最小二乘法求解得

[a,u]T=(BTB)-1BTyn.

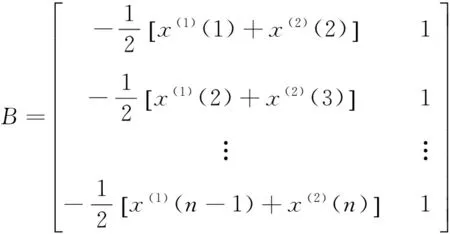
求解微分方程得

通過累減還原，得到x(0)的預測模型為

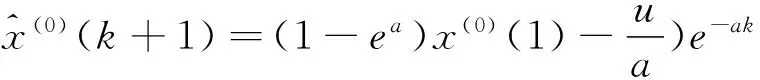
k=1,2,…,n.

(4)

1.2 ARMA模型

若時間序列的數據項Xt可以由該數據項前面的數據項Xt-1,Xt-2,…Xt-m和隨機項αt以及前面的隨機項αt-1,αt-2,…αt-m線性表示出來[9-11]，即為

Xt=αt+f1Xt-1+f2Xt-2+…+fmXt-m-

稱為自回歸移動平均模型，記為ARMA(m,n)模型。其中，m為自回歸的階數；n為滑動的階數。

1.3 粒子群算法

在粒子群算法(PSO)中，每個粒子都被當作目標問題的一個潛在解，粒子以一定的速度向目標逼近，且通過一個目標函數(適應值)來判斷每個粒子與目標之間的距離遠近[12-15]。距離最近的視為當前的最優粒子，其他所有粒子都將據此追隨，經過逐次搜索后得到問題的最優解。每代粒子根據自身及同伴的飛行經驗更新自身，也就是追蹤兩個極值，一是粒子自身經驗的最優解Pbest，另一個就是整個種群社會經驗的最優解gbest。

假設粒子的搜索空間是N維的，種群中粒子數為m,其中第i個粒子的位置為xi=(xi1,xi2…xiN)，將粒子的位置向量代入適應值函數f(x)計算出其適應值大小，評價粒子位置的優劣，粒子的運動速率為向量vi=(vi1,vi2…viN)，第i個粒子從開始到當前為止的最優位置是Pbest=(pi1,pi2…piN)，整個粒子群從開始到當前為止的最優位置是gbest=(g1,g2…gN)。粒子群算法根據式(6)和式(7)來更新粒子的速度和位置。

vin(t+1)=w*vin(t)+c1φ1*(pin(t)-xin(t))+

vin(t+1)=xin(t)+vin(t+1).

(7)

式中:i=1,2,…，m;n=1,2,…,N，t為當前迭代的代數;vin是第i個粒子的速度第n維分量;xi是第i個粒子的位置第i維分量;w為慣性因子;c1,c2是學習因子;φ1,φ2是0到1之間的隨機數，pin代表粒子i個體當前最好位置的第n維分量，gin代表粒種群當前最好位置的第n個分量。

2 粒子群算法的組合模型

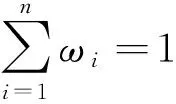
設預測偏差為

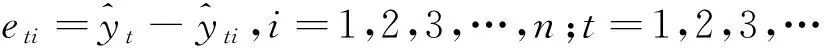
組合預測的最優權重求解，是對誤差平方和在最小二乘準則下求解如下數學問題：

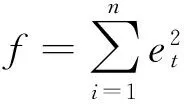
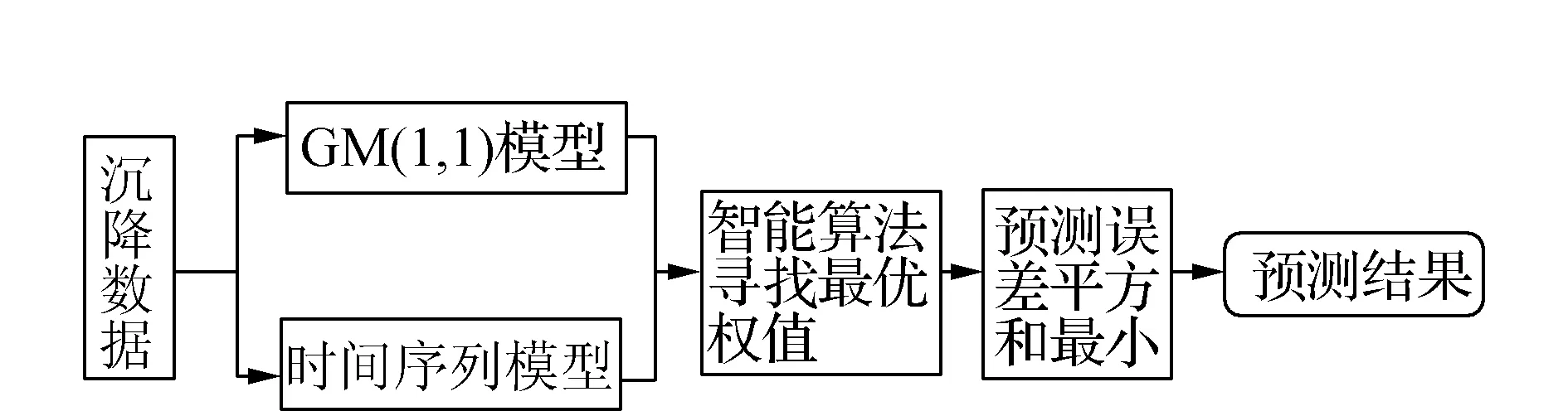
圖1 組合模型結構圖

3 實例分析

本文以廣州某基坑監測項目為例，共有21期沉降數據(見表1)，數據預處理后，對前18期數據分別使用GM(1,1)模型和ARMA模型進行處理，然后采用粒子群算法尋找最優權值，進而構建組合模型對后3期沉降進行預測。

各單項模型處理結果見表1，其中1～18期為模型擬合值，19～21期為預測值。

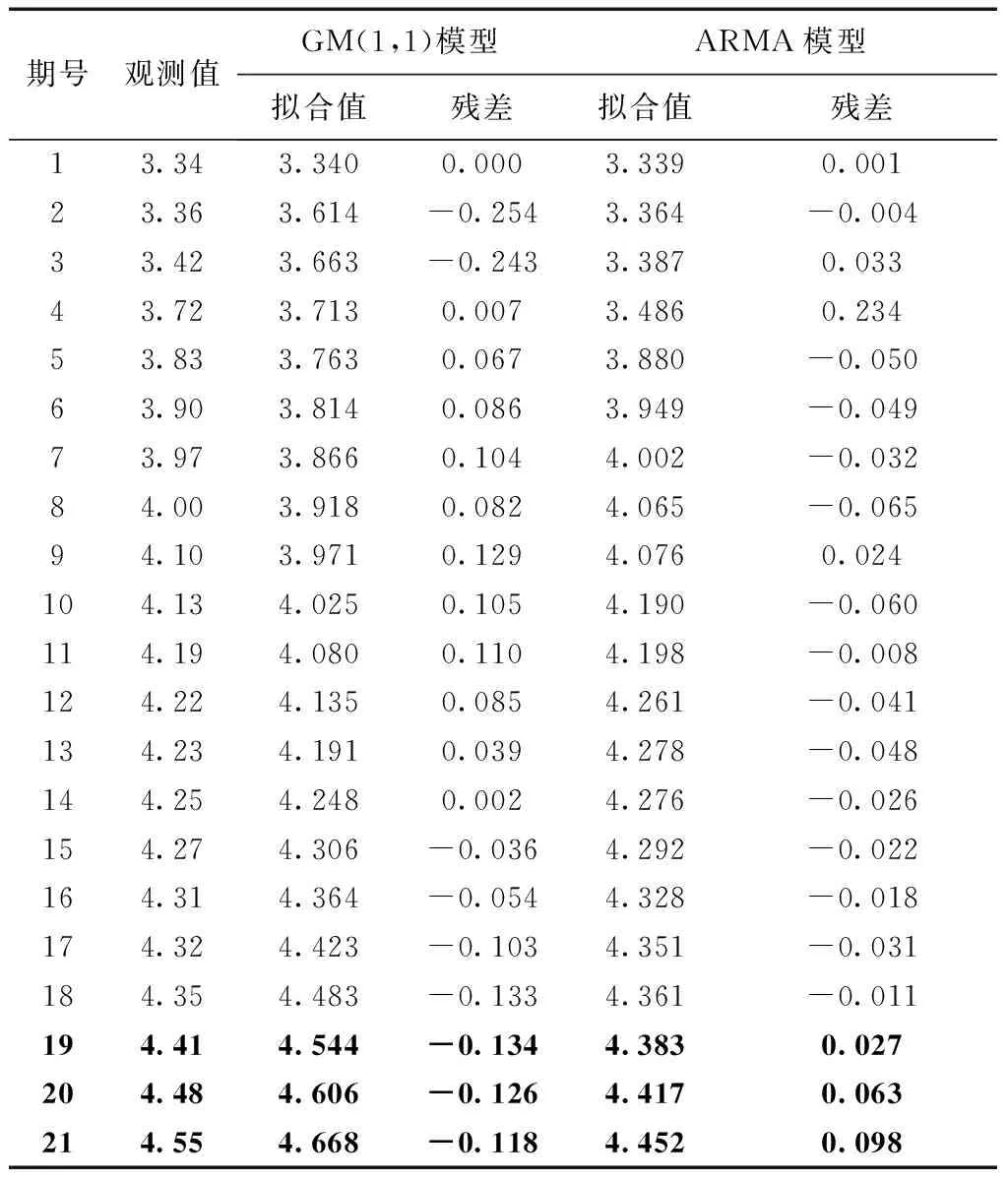
表1 單項模型處理結果 mm

采用粒子群算法(PSO)進行單項模型權值尋優，初始隨機生成30個粒子，進化50次，學習因子c1，c2取1.494 45，慣性權重w取0.7。粒子初始分布位置如圖2所示。

圖2 粒子初始位置分布圖

由圖2可見，粒子初始化后，呈現隨機分布特征，經過尋優查找，最優個體適應度值不斷下降，下降過程如圖3所示。

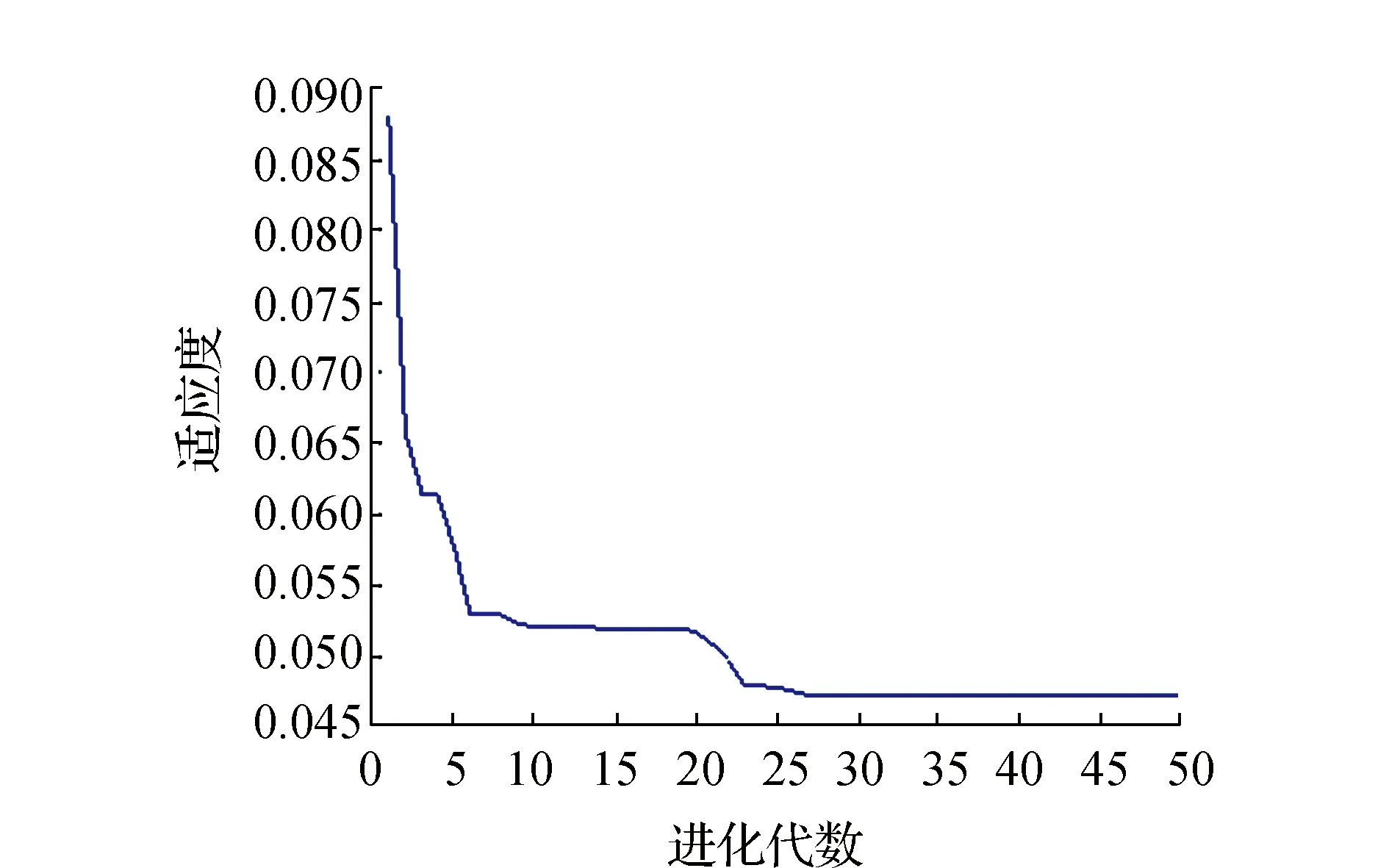
圖3 最優個體適應度變化圖

尋優后，絕大部分粒子非常靠近最優值，分布位置非常集中，粒子的最終分布位置如圖4所示。其中每個粒子所對應的橫軸代表的是GM(1,1)模型的權值，縱軸代表的是ARMA模型的權值。

圖4 粒子最終分布位置圖

經解算，最終尋找到的GM(1,1)模型的組合權值ω1為0.275 7，時序模型的組合權值ω2為0.722 3，故組合模型的表達式為

yt=0.275 7y1+0.722 3y2.

(10)

使用組合模型進行沉降預測，預測結果與單項模型的對比見表2、表3和圖5。

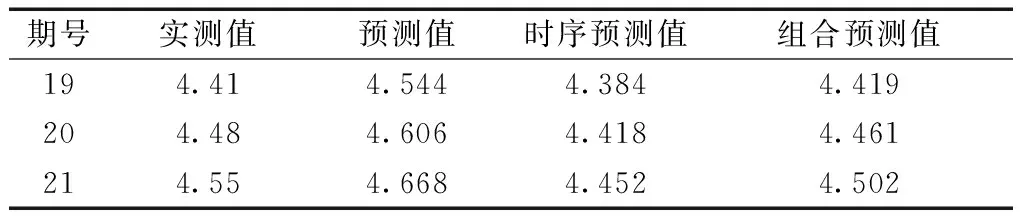
表2 模型預測結果對比 mm

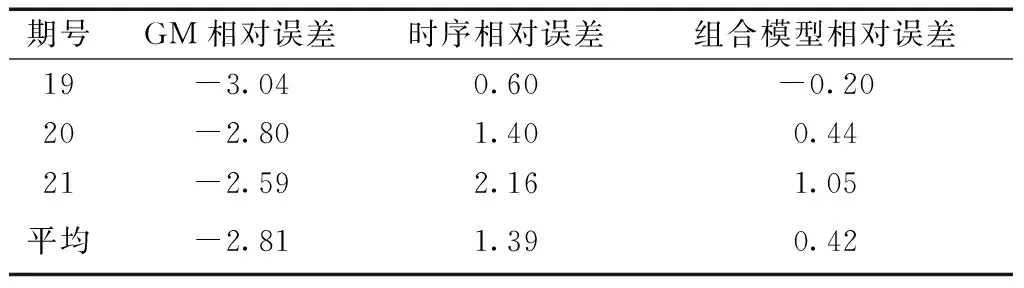
表3 預測結果相對誤差對比 %

由表3和圖5可知，采用粒子群算法進行單項模型權值尋優后，構建的組合模型預測誤差小于兩種單項模型，獲得較高的預測精度，較好地融合灰色GM(1,1)模型和時序ARMA模型的優勢。

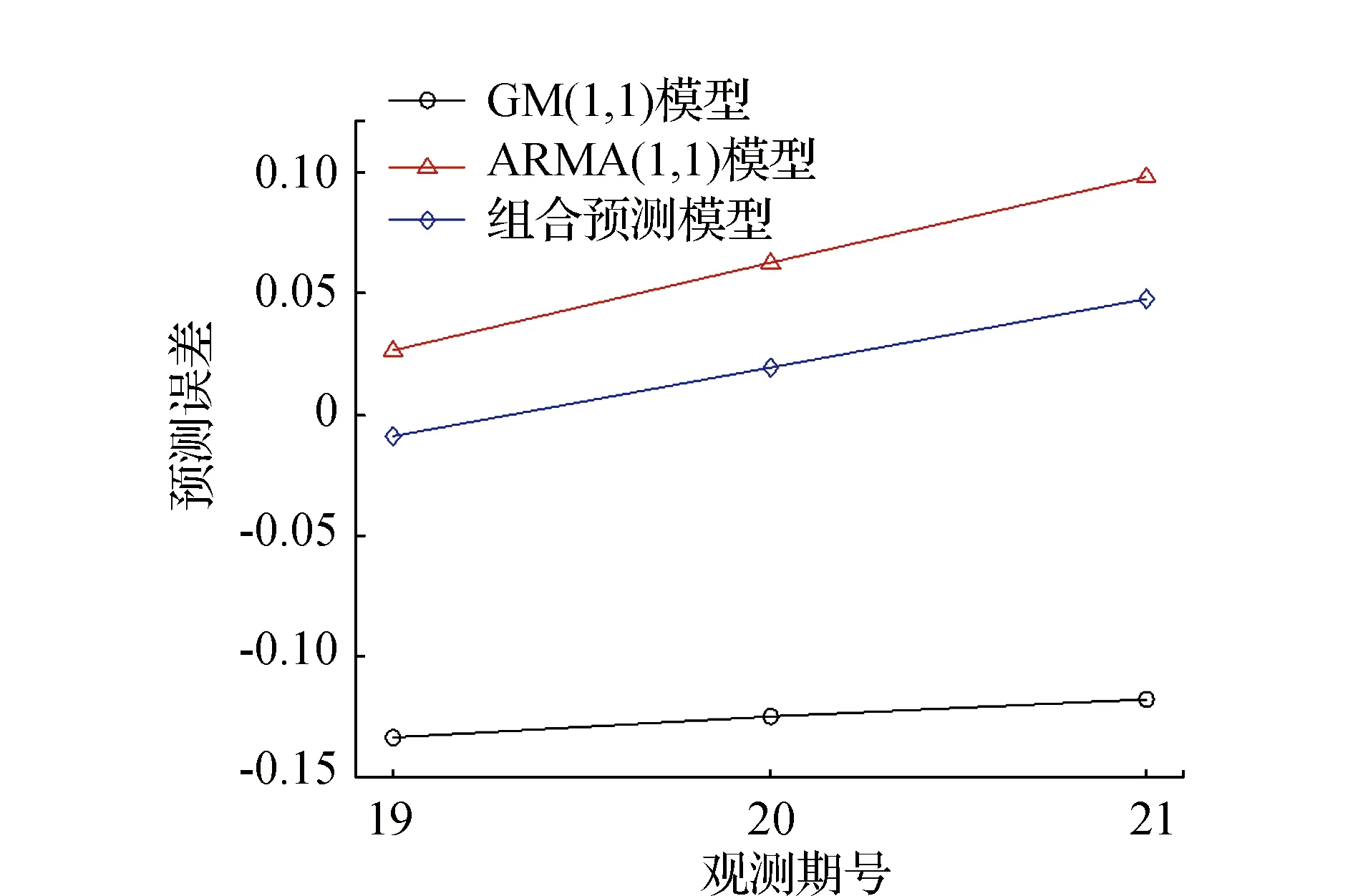
圖5 3種模型預測誤差對比

4 結束語

在變形監測數據處理中,不同的單項模型具有各自的優點和不足，將不同的預測模型以恰當的模式構建組合預測模型，可以發揮各單項模型的優勢，充分利用觀測成果，更好地反映系統的變化規律。本文采用粒子群算法求解組合模型中單項模型的權值，避免求解線性規劃問題。結果表明，該方法構建的組合模型實現較好的預測效果，具有一定的實用價值。

[1] 黃聲享，尹暉，蔣征.變形監測數據處理[M].2版.武漢:武漢大學出版社,2010.

[2] 單銳，王淑花，高東蓮，等.基于時間序列模型與灰色模型的組合預測模型的研究[J].燕山大學學報，2013,36(1)：79-83.

[3] 何書元.應用時間序列分析[M].北京:北京大學出版社，2003：3-20.

[4] 劉燕芳，陳啟華，丁林磊.灰色組合模型在變形預測中的應用[J].工程勘察，2013(1)：58-60.

[5] 鄧聚龍.灰色系統基本方法[M].武漢：華中理工大學出版社，1987:15-39.

[6] 徐秀杰，黃張裕，劉國超，等.改進的灰色GM-AR組合模型在基坑監測數據處理中的應用[J].測繪與空間地理信息，2015,38(1)：200-203.

[7] 袁豹，岳東杰，李成仁.基于總體最小二乘的改進GM(1,1)模型及其在建筑物沉降預測中的應用[J].測繪工程,2013,22(3):52-55.

[8] 楊富春,黃張裕,賈瑩媛,等.基于GM(1,1)灰色模型衛星鐘差短期預報的精度分析[J].測繪工程，2012，21(5):25-29.

[9] 劉娜，欒元重，黃曉陽，等.基于時間序列分析的橋梁變形監測預報研究[J].測繪科學，2011，36(6)：46-48.

[10] 張松,田林亞.時間序列分析在地鐵沉降監測中的應用[J].測繪工程,2014,23(10):63-66.

[11] 唐爭氣,譚志強.灰色時序組合模型在基坑監測中的運用[J].測繪工程,2014,23(2):49-53.

[12] 李博.粒子群優化算法及其在神經網絡中的應用[D].大連：大連理工大學，2005:3-4.

[13] 李愛國，覃征，鮑復民，等.粒子群優化算法[J]．計算機工程與應用，2002(21):1-3.

[14] 薛婷.粒子群優化算法的研究與改進[D].大連:大連海事大學，2008:11-15.

[15] 王維博.粒子群優化算法研究及其應用[D].成都：西南交通大學，2012：16-19.

[責任編輯：張德福]

Application of combined model based on particle swarm optimization in deformation analysis

WANG Xianpeng1,2，HUANG Shengxiang2，LI Guanqing2

(1.Guangzhou Zengcheng Land Resources and Urban Planning Bureau,Guangzhou 511300,China;2.School of Geodesy & Geomatics,Wuhan University,Wuhan 430079,China)

In a parallel combined model being built to predict deformation,one of a key issue is to determine the weights of individual model.This paper takes the deformation data of foundation pit as an example,by using GM (1,1) model and ARMA model to integrate a combination model and adopting the particle swarm optimization to search the optimal weights of two single models under the principle of minimum fitting error sum of squares.The results show that the method can integrate the advantages of each individual model to improve prediction accuracy,without solving linear programming problems,and can be practical.

PSO; GM(1,1) model; ARMA model; combined model; deformation analysis

引用著錄：王顯鵬，黃聲享，李冠青.基于粒子群算法的組合模型在變形分析中的應用[J].測繪工程，2017，26(1)：73-76.

10.19349/j.cnki.issn1006-7949.2017.01.016

2015-12-24

國家自然科學基金資助項目(41274020)

王顯鵬(1991-)，男，碩士.

TU196

A

1006-7949(2017)01-0073-04