飛行器雙自由度耦合振蕩的數值模擬方法

肖中云，劉剛，江雄，王建濤

中國空氣動力研究與發展中心 計算空氣動力研究所，綿陽 621000

飛行器雙自由度耦合振蕩的數值模擬方法

肖中云*，劉剛，江雄，王建濤

中國空氣動力研究與發展中心 計算空氣動力研究所，綿陽 621000

針對模擬雙自由度(2DOF)運動的“PQR”強迫振蕩試驗裝置，通過坐標變換，將機構運動轉化為空間歐拉角進行表示，實現對機構俯仰/偏航、俯仰/滾轉和偏航/滾轉等3種耦合運動的統一描述，采用預定運動軌跡的動網格計算技術，構造了基于非定常雷諾平均Navier-Stokes (URANS)方程的飛行器雙自由度振蕩數值模擬方法。圍繞某復雜構型飛行器低速流動，在模型迎角10°、滾轉角±40°、偏航角±40°振蕩預設條件下分別對單自由度偏航、滾轉振蕩和雙自由度偏航/滾轉振蕩進行了模擬，得到的氣動系數遲滯回線在形態和量值上與風洞試驗結果吻合，證明當前方法可以作為飛行器復雜耦合運動的一種有效研究手段。針對偏航/滾轉耦合振蕩，從運動形式和氣動特性上與單獨偏航、滾轉運動進行了對比分析，結果表明，耦合運動在氣流角、繞體軸的旋轉角速度等方面與單自由度疊加效果不同，力矩系數遲滯回線存在曲線交叉的現象，表現出與單自由度振蕩不同的阻尼特性。在當前模擬狀態下，偏航/滾轉振蕩流場以橫向分離渦運動為主要特征，可以推測大迎角情況下縱橫向分離渦流動結構更加復雜，耦合作用更強，需要進一步在分離流模擬方法上開展研究。

雙自由度；大幅振蕩；耦合運動；非定常；數值模擬

飛行器過失速機動是一種大迎角下的多自由度耦合運動，氣動力呈現出嚴重的非對稱、非線性和非定常特性，由各種實驗數據線性疊加形成總的氣動系數的方法，理論上缺少依據，實際上會存在很大偏差。圍繞過失速機動問題，世界各航空發達國家都開發了相應的風洞試驗與理論分析方法[1-5]，目的是為了獲取飛行器在大迎角過失速區域的非線性、非定常氣動力特性，有助于更好理解動態空氣動力的復雜現象，以及幫助發展更好的飛行力學數學模型。

隨著對飛行器過失速機動能力的日益重視，國內外發展了大量的風洞動態試驗技術[6-8]，包括大迎角動導數、旋轉天平、旋轉振蕩、大幅振蕩試驗技術等。“PQR”動態試驗系統是一種典型的大振幅雙自由度試驗裝置，可進行大幅俯仰、偏航、滾轉振蕩及其雙自由度耦合振蕩、大幅俯仰拉升及俯仰和滾轉耦合拉升試驗[9]。大幅振蕩試驗是進行飛行機動模擬，特別是過失速機動模擬的基本試驗數據。目前單自由度振蕩(俯仰、偏航和滾轉)已經開展了較多的研究，在獲取動導數、動態非定常時間遲滯效應上十分有效，同時可以用于模擬簡單的機動飛行動作，如眼鏡蛇機動和機翼搖滾等。對于復雜機動飛行動作來說，運動通常為多個自由度的耦合運動，如Herbst機動，飛行器在大迎角下同時包含了偏航和滾轉的耦合運動。這就要求不斷提高試驗模擬的運動相似性，從單自由度向雙自由度耦合、多自由度機動的方向發展。

雙自由度振蕩是一種復合運動，運動參數包括平均角度、振幅、振蕩頻率、相位等，各參數的組合情況非常多，運動規律及氣動特性十分復雜。文獻[10]較早開展了三角翼的俯仰/滾轉耦合運動試驗研究，后續又開展了典型飛機的偏航/滾轉耦合氣動力試驗[11-12]，模型支撐迎角達到60°，將耦合運動時的氣動特性與單自由度運動疊加得到的氣動特性進行了對比。文獻[13]介紹了生產型低速風洞的雙自由度大幅振蕩試驗技術，在該技術支撐下開展了某復雜構型飛機偏航/滾轉耦合運動非定常氣動力特性試驗研究，獲得了重復性好、可靠性高的試驗數據[14]。以上這些試驗為研究飛行器大迎角氣動特性積累了寶貴經驗，同時也為非定常氣動建模的發展提供了有力支撐[15-17]。

目前，用CFD方法模擬飛行器多自由耦合運動的工作還比較少見。文獻[18]對二維平板機翼前沖、俯仰振蕩以及兩者的合成運動進行了模擬，研究大尺度渦結構對氣動的影響。文獻[19]研究了低雷諾數下的機翼俯仰和下沉運動，以此模擬微型飛行器的非定常空氣動力效應。隨著計算機運算速度的提高，非定常計算可采用的計算規模大幅提高，對分離渦流動、復雜湍流的模擬能力日益增強。發展多自由度大幅振蕩的數值模擬方法，有助于摸清復雜氣動特性背后的流動機理，對風洞試驗起到相互驗證與校核的作用。本文基于描述姿態運動的歐拉角方法和動網格數值計算，發展了模擬飛行器雙自由度大幅振蕩的數值模擬方法，探討了耦合運動的特點及其與解耦運動的關系，最后以偏航/滾轉振蕩為例，通過對某復雜外形飛行器的模擬驗證了本文方法。

1 “PQR”機構的姿態運動描述方法

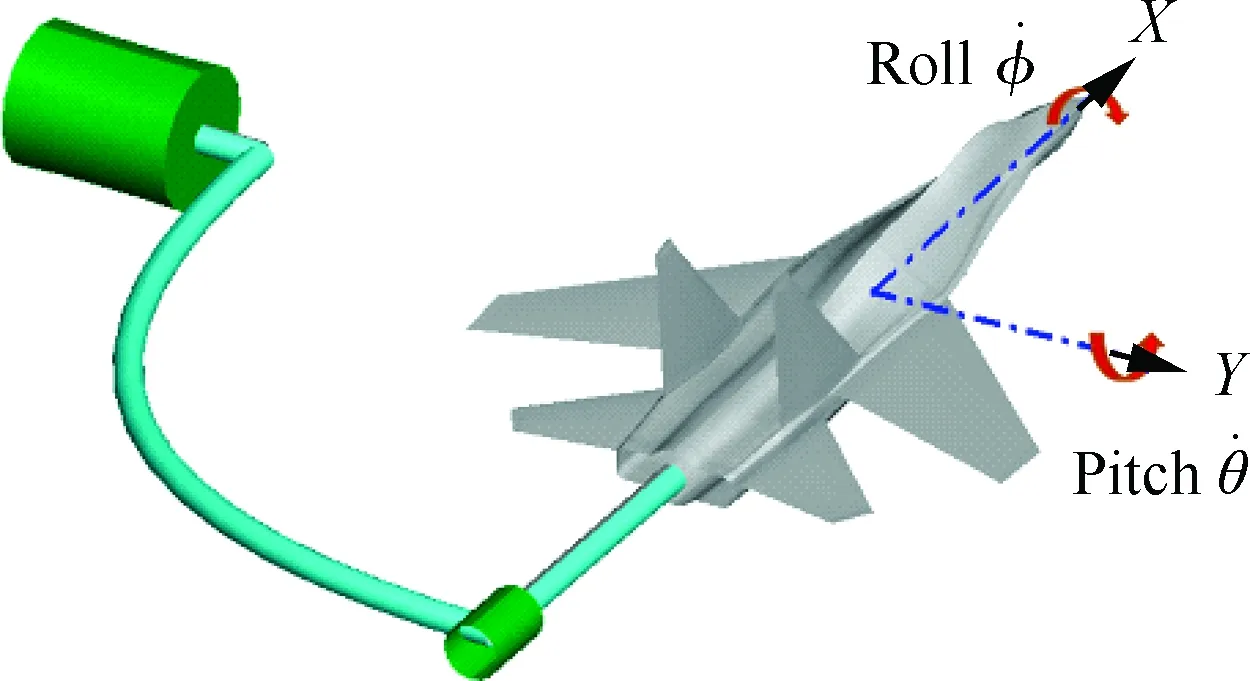
圖1 俯仰/滾轉耦合運動Fig.1 Pitch/roll coupled motion

圖2 偏航/滾轉耦合運動Fig.2 Yaw/roll coupled motion

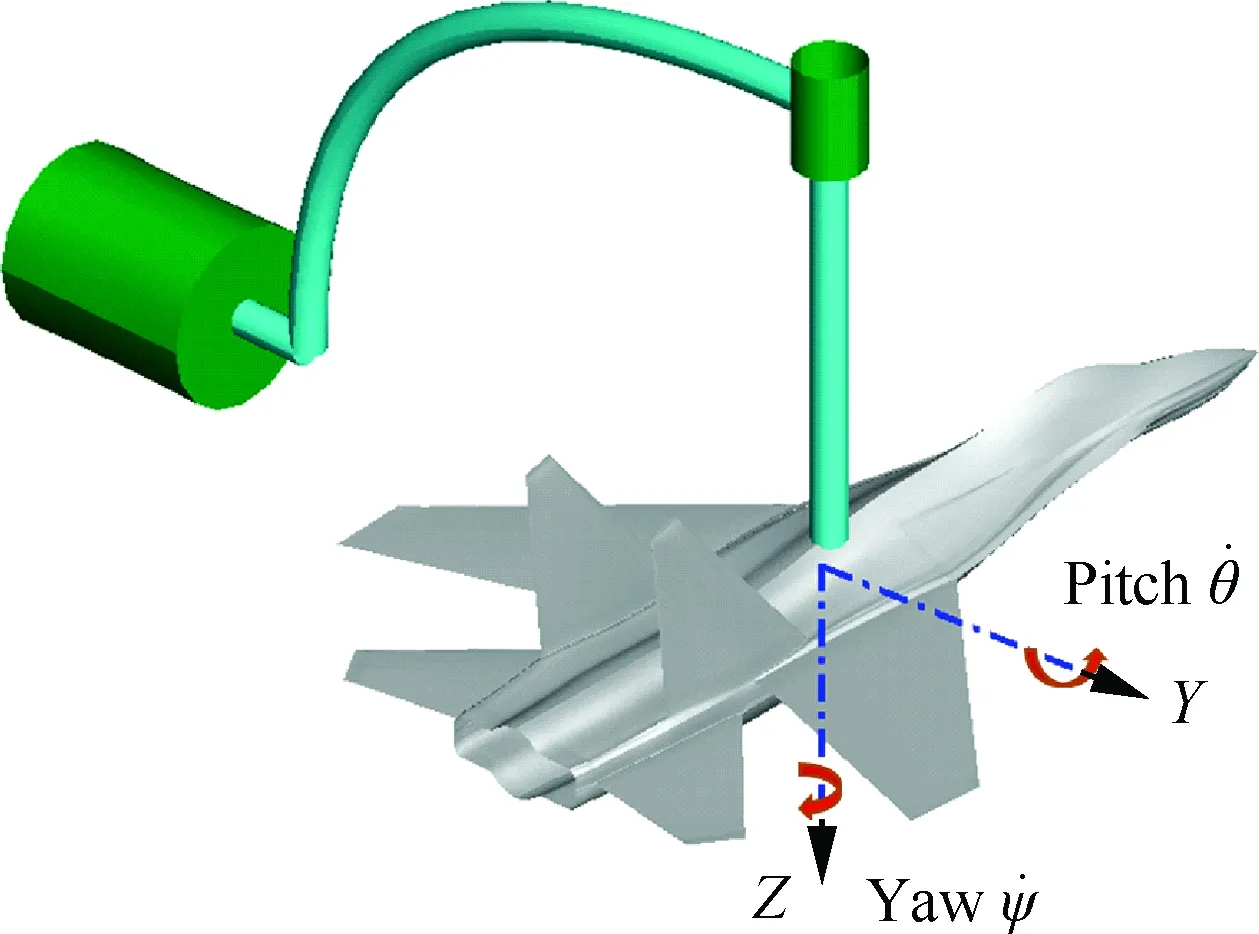
圖3 俯仰/偏航耦合運動Fig.3 Pitch/yaw coupled motion

Aα=I3×3cosα+(1-cosα)e·eT-e×sinα

(1)

式中：I3×3為單位矩陣；e×定義為

將式(1)展開，可得

(2)

繞體軸旋轉的方向余弦矩陣為

(3)

式中：Cα代表cosα,Sα代表sinα,其余類似，兩自由度動態試驗包括了俯仰/滾轉、俯仰/偏航、偏航/滾轉3種類型，為了統一輸入輸出接口，將兩自由度運動定義為“繞體軸旋轉+繞地面系下任意軸旋轉”兩次連續旋轉過程。用Xd和Xt表示地軸系和體軸系下的坐標，Aφ,θ,ψ為繞體軸旋轉的方向余弦矩陣，得到坐標變換關系為

等價于：

Xt=Aφ,θ,ψAαXd

(4)

式(4)說明了雙自由度運動的坐標變換包含了兩次矩陣左乘的運算，注意此時運算結果與乘法順序相關，矩陣的順序不能互換。最后得到的坐標變換矩陣為

A=Aφ,θ,ψAα

(5)

下面考慮方向余弦矩陣向歐拉角的轉換，如果考慮俯仰角在-90°～+90°之間取值，滾轉角和偏航角在-180°～+180°之間取值，則方向余弦矩陣到歐拉角的轉換公式為

(6)

θ=arcsin(-A13)

(7)

(8)

(9)

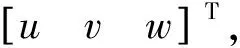
ifu≠0 then

{α=arctan(w/u)

β=arctan(-(vcosα)/u)

elseifw≠0 then

{α=(π/2)sign(w)

β=arctan(-v/w)

elseifw=0 then

{α=π/2

β=(π/2)sign(-v)

2 數值計算方法

流動控制方程采用任意拉格朗日-歐拉(Arbitrary Lagrangian Eulerian，ALE)形式下的可壓縮非定常雷諾平均Navier-Stokes(URANS)方程，允許網格的任意運動和變形，在絕對坐標系下的積分形式為

(10)

式中：Q為守恒變量;Ω表示控制體的體積；S為控制體邊界面的面積;n為單位法向矢量；VΩ為邊界面上的網格運動速度；HI和HV分別為對流通量和黏性通量。非定常計算采用雙時間步方法，其中內層時間離散采用了點隱式LU-SGS方法，真實時間采用了三層二階精度格式離散，在每個真實時間步內通過內層時間迭代使氣動力積分值收斂。黏性離散采用全Navier-Stokes方程方法，湍流采用的是兩方程k-ω剪切應力輸運(SST)模型進行模擬。由于是計算低速大迎角問題，為降低低速流動的剛性，流動控制方程采用了低速預處理方法，同時為加速流場收斂還采用了3重V循環的多重網格方法，每一重網格的迭代步數為5步，每個真實時間步內多重網格循環的最大次數為200步。在當前參數設置下，基本上都能保證子迭代過程的氣動力收斂，如果在迭代過程中密度殘差下降到兩個量級以上，則被認為是子迭代收斂，提前退出循環。

計算模型如圖4所示，平均氣動弦長(參考長度)為0.426 9 m，來流風速為25 m/s，雷諾數Re=1.71×106，第一層網格距離物面5×10-6m，滿足湍流附面層模擬y+=Ο(1)的要求，網格采用多塊對接網格(包括232塊)，單元總數約為1 228萬。

圖4 計算模型和滾轉振蕩瞬時流場Fig.4 Calculation model and instantaneous flow field of roll oscillation

在開展動態計算之前，首先通過靜態流場對計算方法進行校核，模擬迎角α=0°～80°。圖5給出的是計算與試驗的升力系數CL比較，可以看到，在所有迎角范圍內計算與試驗值吻合良好，最大升力系數約為1.48，對應的迎角約為35°。圖6給出的是阻力系數CD曲線比較，可以看到，在迎角α=40°以前，計算與試驗值吻合較好，在α>40°以后，計算值較試驗值偏高，最大偏差量約為10%。圖7給出了俯仰力矩系數Cm的比較，也可以看到兩者之間吻合較好，并且可以看到該飛行器模型在中小迎角范圍內俯仰方向是靜不穩定的，俯仰力矩隨迎角增大而增大，而在大迎角下(α>30°)是俯仰靜穩定的。總的來說，當前計算在規律和趨勢上和試驗值都比較一致，反映了低速大迎角流場的主要特征。由于目前公認的URANS方法模擬大分離流動存在不足，所以認為在失速迎角以后計算與試驗值存在一定偏差是合理的，在當前計算中主要表現在阻力值的預測上。

圖5 升力系數比較Fig.5 Comparison of lift coefficients

圖6 阻力系數比較Fig.6 Comparison of drag coefficients

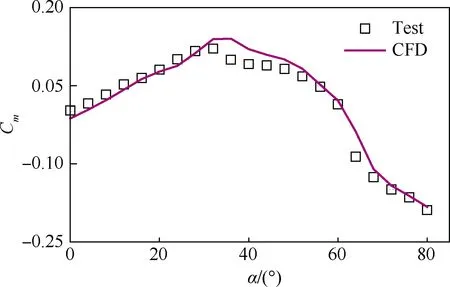
圖7 俯仰力矩系數比較Fig.7 Comparison of pitching moment coefficients

3 計算結果與分析

3.1 偏航、滾轉單自由度大幅振蕩

在計算偏航/滾轉雙自由度振蕩之前，首先對偏航振蕩和滾轉振蕩分別進行計算，單自由度滾轉振蕩的運動規律用正弦函數表示，φ=40°·sin(2πft),振蕩頻率f=0.8 Hz。圖4給出的是計算模型和滾轉振蕩瞬時流場，對應瞬時滾轉角為34.6°，分別給出了橫向截面的馬赫數Ma云圖、空間流線與渦量等值面，可以看到在當前位置下，飛行器左右側旋渦的位置和強度都發生改變，模擬得到的物面邊界層與空間旋渦的形態分布合理。

圖8給出了滾轉和偏航力矩系數(Cl,Cn)的計算值與試驗值比較，可以看到計算與試驗值吻合很好，進一步驗證了當前計算方法的合理性。盡管計算流體力學存在計算坐標系、飛機體軸系之分，這里為敘述方便將角度定義的方向和氣動力矩的方向都統一到機體坐標系下。在轉動方向與力矩方向定義一致的前提下，可以根據力矩曲線的斜率或方向來判斷飛機的力矩特性[10]。具體來說，靜態情況下如果力矩系數的斜率為負，說明在該方向上的力矩是靜穩定的，否則為靜不穩定；在動態情況下，如果遲滯回線沿逆時針方向旋轉，則說明在該方向上的運動對力矩起阻尼作用，如果遲滯回線沿順時針方向旋轉，則說明在該方向上的運動對力矩起發散作用。

圖8 滾轉振蕩的滾轉與偏航力矩系數(α=10°)Fig.8 Roll and yaw moment coefficients in roll oscillation (α=10°)

如圖8所示，對于滾轉力矩來說，從最小滾轉角對應的力矩點和最大滾轉角對應的力矩點之間連線，可以得出滾轉力矩呈左上右下的走勢，即正的滾轉角對應的滾轉力矩為負，說明飛機在滾轉方向上是靜穩定的。但是對當前滾轉大幅振蕩來說，滾轉力矩形成了很大的遲滯圈，即滾轉力矩產生了很強的動態非定常效應。圖中標注了遲滯回線的旋轉方向，可以看到滾轉力矩曲線呈逆時針走向，并且滾轉力矩環呈O型，這說明在整個滾轉角歷程中滾轉運動對滾轉力矩的變化起阻尼作用。圖中同時還給出了偏航力矩的遲滯回線，可以看到當前偏航力矩并非小量，說明飛行器滾轉和偏航之間存在較強的耦合作用，同時偏航力矩遲滯回線的旋轉為逆時針方向，意味著滾轉引起的偏航交叉動導數起阻尼作用。在振蕩過程中，當飛行器處于平衡位置時，圖8中滾轉力矩遲滯圈包圍面積很大，對比上行和下行狀態，當飛行器處于平衡位置時，兩者的姿態角和氣流迎角、側滑角都一致，角速度不同、時間歷程不同，造成了滾轉力矩系數的較大差異。

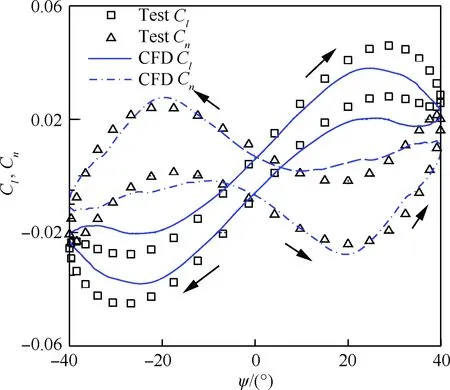
圖9 偏航振蕩的滾轉與偏航力矩系數 (α=10°)Fig.9 Roll and yaw moment coefficients in yaw oscillation (α=10°)

單自由度偏航振蕩的運動規律用正弦函數表示，ψ=40°sin(2πft),振蕩頻率f=0.8 Hz。圖9給出的是偏航振蕩的計算與試驗值比較，包含滾轉和偏航力矩系數，可以看到計算與試驗在趨勢與量值上都比較一致，可以說計算正確反映了偏航運動下的橫航向力矩特性變化，不足之處是在較大偏航角下，計算的偏航力矩與滾轉力矩峰值較試驗值偏小，其余地方兩者都吻合較好。對于偏航力矩來說，在偏航角ψ=-20°～20°區間，偏航力矩呈左高右低的走向，說明此時偏航力矩與運動方向相反，有利于飛行器的穩定；但是在ψ<-20°和ψ>20°的區間，偏航力矩的走向與運動方向相同，不利于偏航方向的穩定。由于偏航力矩主要是飛行器垂尾產生，在較大的偏航角下，垂尾效率下降甚至失速，會導致偏航穩定的效率下降。從總的曲線變化趨勢上看，偏航力矩遲滯環呈逆時針變化，動導數起阻尼作用。另外，由偏航引起的滾轉力矩遲滯環呈順時針變化，偏航引起的滾轉交叉動導數起發散作用。

3.2 偏航/滾轉耦合大幅振蕩

偏航/滾轉耦合的運動機構見圖2，機構偏角定義為

(11)

圖10 偏航/滾轉運動中的歐拉角、迎角和側滑角變化 Fig.10 Euler angle，angle of attack and sideslip angle variations in yaw/roll coupled motion

設定滾轉和偏航的振蕩幅值φA=ψA=40°,振蕩頻率均為f=0.8 Hz,初始相位相同，即飛行器從平衡位置開始向右偏航、向右滾轉。圖10給出的是偏航/滾轉耦合運動下的歐拉角、迎角和側滑角變化曲線，可以看到，在運動過程中俯仰角θ始終為0°，偏航角ψ和滾轉角φ在±40°之間變化，偏航與滾轉方向的歐拉角與機構運動偏角相等。圖中同時給出了迎角、側滑角的變化，其中平衡位置的來流迎角α=10°，可以看到飛行器在姿態角發生變化的同時，氣流角也在發生變化，其中迎角在10°～36°之間變化，側滑角則在±22°之間變化。

圖11給出的是體軸系的3個角速度變化曲線，可以看到，除了偏航和滾轉方向的角速度外，俯仰方向上也產生了角速度，并且俯仰角速度的周期是其他兩個方向角速度周期的一半。由此可以看到，偏航/滾轉耦合運動并不是偏航運動和滾轉運動的簡單疊加，其中包括了多個動態參數的變化，根據線性理論假設，將氣動力/力矩系數通常表示為飛行狀態參數的函數[21]，即

Cj0(α,β,V∞,h,δi)+Cjd(α,β,V∞,h,δi,p)+

Cjd(α,β,V∞,h,δi,q)+…

(12)

圖12給出的是偏航/滾轉振蕩的升力系數CL、阻力系數CD和側向力系數Cy比較，從圖中可以看到，升力系數和阻力系數呈“∞”形變化，側向力系數呈雙“∞”形變化。計算值與試驗值總體上吻合較好，一定程度說明本文算法的正確性，不足之處是最大振蕩角度下計算的升力系數值略小于試驗值，同時也導致了該角度下的阻力系數較試驗值小。

圖11 偏航/滾轉運動中的體軸系角速度變化Fig.11 Angular velocity variations of body axial system in yaw/roll coupled motion

滾轉力矩和偏航力矩變化是偏航/滾轉耦合振蕩重點關注的對象。圖13給出了滾轉力矩系數隨滾轉角變化曲線。可以看到當前力矩曲線呈兩個“∞”形分布，在滾轉角-18°<φ<18° 區域，曲線為逆時針旋轉，說明滾轉動導數起阻尼作用，而在φ<-18°和φ>18°的兩個區域，曲線為順時針旋轉，說明此時滾轉動導數起發散作用。

圖14給出了耦合振蕩下的偏航力矩系數變化曲線，可以看到當前曲線的旋轉方向為逆時針，說明耦合振蕩引起的偏航動導數起阻尼作用。圖13和圖14分別給出了滾轉和偏航力矩系數的風洞試驗值，從計算值與試驗值的比較來看，兩者在曲線形態和量值上都吻合較好，說明當前采用的計算方法是合理的。

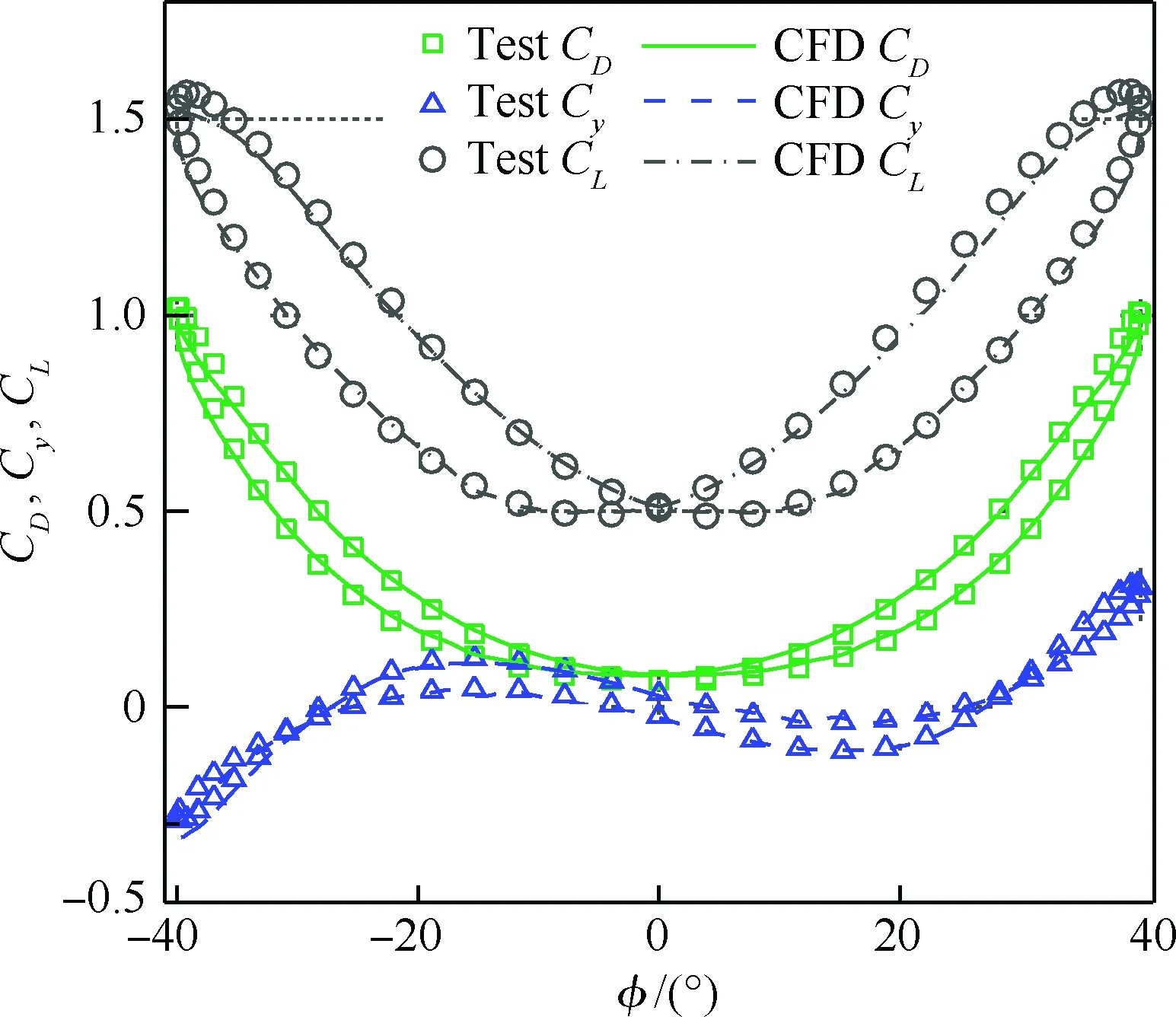
圖12 偏航/滾轉振蕩的升力、阻力和側向力系數比較Fig.12 Comparison of lift, drag and side force coefficients in yaw/roll oscillation

圖13 偏航/滾轉振蕩的滾轉力矩系數Fig.13 Roll moment coefficients in yaw/roll oscillation

圖14 偏航/滾轉振蕩的偏航力矩系數Fig.14 Yaw moment coefficients in yaw/roll oscillation

圖15 耦合運動與單獨運動疊加的偏航力矩系數比較Fig.15 Comparison of yaw moment coefficients between couple motion and single freedom motion addition

下面考慮耦合運動與單獨運動疊加結果的比較，圖15給出的是偏航力矩系數曲線，可以看到耦合結果與疊加結果具有較高的相似性，并且與單獨偏航運動的結果相似，可見該飛行器的偏航力矩主要由偏航運動產生，相比之下滾轉振蕩產生的偏航力矩較小。圖16給出的是滾轉力矩系數曲線，可以看到，當前耦合運動的力矩系數在大的趨勢上與圖9偏航振蕩比較相近，呈左下右上的分布形態。經過簡單疊加得到的力矩曲線在較大滾轉角范圍內(-32°<φ<32°)都是沿逆時針方向旋轉，在φ>32°和φ<-32°之后曲線出現了交叉，但包圍的面積很小。出現交叉的原因是滾轉運動和偏航運動的力矩曲線旋轉方向相反，具體來說，滾轉運動產生的滾轉力矩系數曲線沿逆時針方向旋轉，偏航運動產生的滾轉力矩系數沿順時針方向旋轉。與單獨運動疊加對比，耦合運動在小滾轉角下表現出了類似的形態，力矩曲線沿逆時針方向旋轉，不同的是當滾轉角較大時(φ>18°和φ<-18°)，力矩曲線出現了交叉，旋轉方向變為順時針，并且每個順時針旋轉曲線包圍的面積較大，與逆時針旋轉所包圍的面積相當。

另外，由于耦合運動的滾轉力矩曲線形態發生改變，當飛行器從平衡位置向右側滾轉時，隨滾轉角增大時，滾轉力矩加速上揚，在φ=34°附近達到最大值，該值較單獨運動和單獨運動疊加對應的滾轉力矩要高出很多，力矩的作用方向是進一步加速飛行器的滾轉運動。

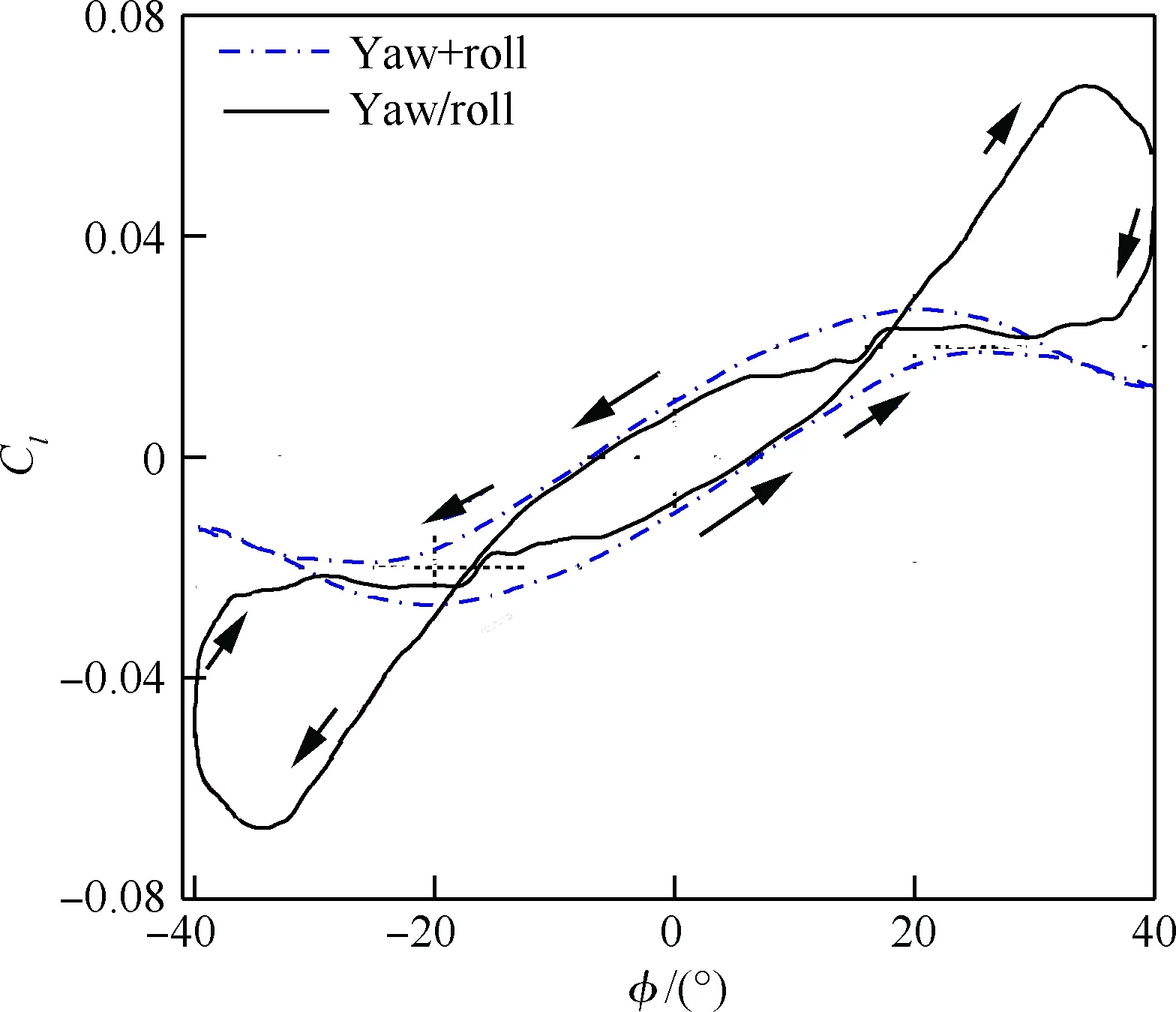
圖16 耦合運動與單獨運動疊加的滾轉力矩系數比較Fig.16 Comparison of roll moment coefficients between couple motion and single freedom motion addition

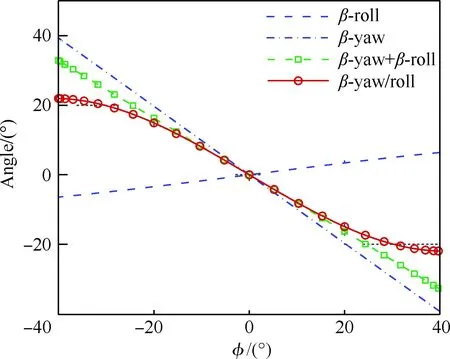
圖17 耦合運動與單獨運動疊加的側滑角比較Fig.17 Comparison of side slip angles between couple motion and single freedom motion addition

為了弄清力矩曲線變化的原因，首先對耦合運動的姿態角與氣流角變化進行了分析，從圖10可以看到，耦合運動除了偏航和滾轉方向的姿態角變化以外，可能對滾轉力矩產生較大影響的是側滑角的變化。為進一步分析，圖17對單獨運動和耦合運動的側滑角進行了比較，可以看見，單獨偏航運動的側滑角在[-40°,40°] 區間變化，單獨滾轉運動的側滑角在[-6.4°,6.4°] 區間變化，但方向相反，耦合運動的側滑角約在[-22°,22°] 區間變化。從圖9知道，偏航運動當偏航角在25°之前產生的滾轉力矩單調上升，25°以后開始下降，這其中起主導作用的就是側滑角的變化。而對于耦合運動來說，側滑角始終在±25°內變化，該角度范圍不足以使垂尾發生失速，使滾轉力矩得以持續上升，這也就解釋了圖16耦合振蕩的滾轉力矩系數峰值增大的原因。從本文分析可以看到，非定常氣動系數的影響因素很多，包括模型姿態角、氣流角、對應角速度等，非定常運動的時間歷程效應也是影響因素之一，這些因素的疊加導致了耦合運動氣動特性的復雜性，同時給氣動系數建模帶來了難度。

4 結 論

采用URANS方法模擬預定運動軌跡,建立了專門針對飛行器雙自由度大振幅振蕩的數值模擬方法，完成了某復雜外形飛行器靜態、偏航振蕩、滾轉振蕩和偏航/滾轉耦合振蕩的模擬，結合試驗數據對力矩特性的分布規律進行了分析。

1) “PQR”試驗裝置在進行雙自由度試驗時，模型方位與旋轉順序無關，在用CFD進行預定軌跡計算時，將用戶輸入用一次繞任意軸旋轉疊加一次繞體軸旋轉表示，輸出用坐標變換的歐拉角及繞體軸的角速度表示，可以實現對任意俯仰/偏航、俯仰/滾轉、偏航/滾轉等耦合運動的描述。

2) 當前計算采用了低速預處理、多重網格等加速收斂技術，保證非定常計算每個子迭代過程氣動力的充分收斂，得到的計算結果合理，在模型平衡位置迎角10°，滾轉±40°偏角、偏航±40°偏角下的結果與風洞試驗值吻合一致。

3) 飛行器雙自由度運動不是兩個單自由度運動的簡單疊加，氣動特性具有單自由度運動的部分特點，但遲滯回線的形態更加復雜，甚至表現出不同的運動阻尼特性。

4) 本文偏航/滾轉耦合振蕩的平衡位置迎角為10°，流場以橫向分離渦運動為主要特征，可以推測大迎角情況下縱橫向分離渦流動結構更加復雜，耦合作用更強，需要進一步在大分離流模擬方法上開展研究。

本文模擬外形為1∶16風洞縮尺模型，來流風速為25 m/s，基于平均氣動弦長的雷諾數為百萬量級，當前條件下本文URANS方法取得了與試驗值比較吻合的結果，真實飛行條件下飛行器速度更快、雷諾數更高，對計算方法構成挑戰。下一步有必要開展真實飛行條件下的計算研究，依托高雷諾數風洞試驗來驗證CFD方法；同時分離渦流動模擬是當前的熱門研究方向，開展這類方法研究將有助于解決大迎角大分離流動的動態模擬問題。

致 謝

本研究得到了汪清研究員、劉志濤副研究員的幫助和指導，在此表示感謝。

[1] NELSON R C, PELLETIER A. The unsteady aerodynamics of slender wings and aircraft undergoing large amplitude maneuvers[J]. Progress in Aerospace Sciences, 2003, 39(2): 185-248.

[2] KRAMER B R. Experimental evaluation of superposition techniques applied to dynamic aerodynamics: AIAA-2002-0700[R]. Reston, VA: AIAA, 2002.

[3] LAN C E, LI J, YAU W, et al. Longitudinal and lateral-directional coupling effects on nonlinear unsteady aeodynamic modeling from flight data: AIAA-2002-4804[R]. Reston, VA： AIAA, 2002.

[4] WANG Z, LAN C E, BRANDON J M. Fuzzy logic modeling of lateral-directional unsteady aerodynamics：AIAA-1999-4012[R]. Reston, VA： AIAA, 1999.

[5] JENKINS J E. Nonlinear aerodynamic characteristics of a 65 degree delta wing in rolling motion: Implications for testing and flight mechanics analysis：AIAA-1997-0742[R].Reston, VA： AIAA, 1997.

[6] OWENS D B, BRANDON J M, CROOM M A, et al. Overview of dynamic test techniques for flight dynamics research at NASA LaRC: AIAA-2006-3146[R]. Reston, VA： AIAA, 2006.

[7] GILLARD W J. AFRL F-22 dynamic wind tunnel test results: AIAA-1999-04015[R]. Reston, VA： AIAA, 1999.

[8] 李偉. 飛機大振幅動態實驗及其非定常氣動特性研究[D]. 南京: 南京航空航天大學, 2008.

LI W. Unsteady aerodynamic experiments and characteristics for the aircraft oscillation in large amplitude[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008 (in Chinese).

[9] 李周復. 風洞特種試驗技術[M]. 北京: 航空工業出版社, 2010.

LI Z F. Special test technology in wind tunnel[M]. Beijing: Aviation Industry Press, 2010 (in Chinese).

[10] 黃達, 吳根興. 三角翼俯仰滾轉耦合運動氣動特性研究[J]. 航空學報, 1999, 20(6): 485-488.

HUANG D, WU G X. Investigation of unsteady aerodynamic characteristics for a delta wing oscillating in large amplitude pitching roll motion[J]. Acta Aeronautica et Astronautica Sinica, 1999, 20(6): 485-488 (in Chinese).

[11] 黃達, 吳根興. 飛機偏航-滾轉耦合運動非定常空氣動力實驗[J]. 南京航空航天大學學報, 2005, 37(4): 408-411.

HUANG D, WU G X. Experiment on fighter oscillating in large amplitude yaw-roll motion[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2005, 37(4): 408-411 (in chinese) .

[12] HUANG D, WU G X. Unsteady rolling moment characteristics for fighter oscillating with yawing-rolling coupled motion[J]. Journal of Aircraft, 2006, 43(5): 1570-1573.

[13] 劉春明, 趙志軍, 卜忱. 低速風洞雙自由度大幅振蕩試驗技術[J]. 航空學報, 2016, 37(8): 2417-2425.

LIU C M, ZHAO Z J, BU C， et al. Double degree-of-freedom large amplitude oscillation test technology in low speed wind tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2417-2425 (in Chinese).

[14] 楊文, 卜忱, 眭建軍. 某復雜構型飛機偏航-滾轉耦合運動非定常氣動力特性實驗研究[J]. 實驗流體力學, 2016, 30(3): 61-65.

YANG W, BU C, GUI J J. Investigation of the unsteady aerodynamic characteristics of a fighter with complex configuration undergoing yaw-roll coupling oscillation motion[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(3): 61-65 (in Chinese).

[15] 孫海生, 張海酉, 劉志濤. 大迎角非定常氣動力建模方法研究[J]. 空氣動力學學報, 2011, 29(6): 733-737.

SUN H S, ZHANG H Y, LIU Z T. Comparative evaluation of unsteady aerodynamics modeling approaches at high angle of attack[J]. Acta Aerodynamica Sinica, 2011, 29(6): 733-737 (in Chinese).

[16] 汪清, 錢煒祺, 丁娣. 飛機大迎角非定常氣動力建模研究進展[J]. 航空學報, 2016, 37(8): 2332-2347.

WANG Q, QIAN W Q, DING D. A review of unsteady aeeodynamic modeling of aircrafts at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2332-2347 (in Chinese).

[17] 史志偉, 黃達, 吳根興, 等. 耦合運動非定常氣動模型對飛機飛行特性仿真的影響[J]. 航空學報, 2008, 29(6): 1424-1428.

SHI Z W, HUANG D, WU G X, et al. Effects of coupled motion unsteady aerodynamic model on flight characteristics simulation of aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1424-1428 (in Chinese).

[18] JANTZEN R, TAIRA K. Aerodynamic force modeling for unsteady wing maneuvers: AIAA-2014-0223[R]. Reston, VA: AIAA, 2014.

[19] MICHAEL V L. The high frequency, high-amplitude pitch problem: Airfoils, plates and wings: AIAA-2009-3686[R]. Reston, VA: AIAA, 2009.

[20] 張帆, 曹喜濱, 鄒經湘. 一種新的全角度四元數與歐拉角的轉換算法[J]. 南京理工大學學報, 2002, 26(4): 376-380.

ZHANG F, CAO X B, ZOU J X. A new large-scale transformation algorithm of quaternion to Euler angle[J]. Journal of Nanjing University of Science and Technology, 2002, 26(4): 376-380 (in Chinese).

[21] WANG F J, CHEN L. Numerical prediction of stability derivatives for complex configurations[J]. Procedia Engineering, 2015, 99(1): 1561-1575.

Numericalsimulationmethodsfor2DOFcoupledoscillationsofaircraft

XIAOZhongyun*,LIUGang,JIANGXiong,WANGJiantao

ComputationalAerodynamicsInstitute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

Focusingonthe“PQR”forcedoscillationtestapparatusformodelingTwo-Degree-of-Freedom(2DOF)motions,coordinatetransformationisperformedtoobtainunifiedEulerangledescriptionsofthepitch/yaw,pitch/rollandyaw/rollcoupledmotions.BasedonmovinggridsforprescribedmotionandUnsteadyReynoldsAveragedNavier-Stokes(URANS)equations,anumericalalgorithmisdevelopedtosimulatecoupledoscillationofaircrafts.Surroundinglowspeedflowsofacomplexaircraft,single-degreeoscillationsofyawandrollandyaw/rollcoupledoscillationarerespectivelycomputedatangleofattackof10°andamplitudeofoscillationof40°.Thenumericalresultsagreewellwiththeexperimentaldata,showingthatcurrentalgorithmhaspromisingpotentialsinsimulationofcomplicatedcoupledmotionsofaircrafts.Asformovingprocessandaerodynamics,theyaw/rollcoupledmotioniscomparedwiththesuperpositionofsingleyawandrolloscillations,whichshowsthatdifferencesexistinbodyangularvelocitiesandflowangles,andthemomenthysteresiscurveoftheyaw/rollcoupledmotionshowscrossings,indicatingtotallydifferentdampingcharacteristicsfromsingleDOFoscillation.Incurrentyawandrolloscillations,flowsarecharacterizedbylaterallyseparatedvortexes.Itisassumedthatathighangleofattack,whenflowsaremorecomplicatedwithlateralandlongitudinalvortexesandstrongcoupledeffects,morestudiesshouldbedoneonnumericalmethodsofhighlyseparatedflows.

2DOF;largeamplitudeoscillation;coupledmotion;unsteady;numericalsimulation

2017-04-21；Revised2017-05-16；Accepted2017-06-07；Publishedonline2017-06-161118

URL：http://hkxb.buaa.edu.cn/CN/html/20171111.html

s：NationalBasicResearchProgramofChina(613221)；NationalNaturalScienceFoundationofChina(11572341);NationalKeyResearchandDevelopmentProgram(2016YFB0200704)

.E-mailscxiaozy@sina.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121345

V211.3

A

1000-6893(2017)11-121345-10

2017-04-21；退修日期2017-05-16；錄用日期2017-06-07；< class="emphasis_bold">網絡出版時間

時間：2017-06-161118

http://hkxb.buaa.edu.cn/CN/html/20171111.html

國家“973”計劃(613221)； 國家自然科學基金(11572341)； 國家重點研發計劃(2016YFB0200704)

.E-mailscxiaozy@sina.cn

肖中云，劉剛，江雄，等．飛行器雙自由度耦合振蕩的數值模擬方法J． 航空學報,2017,38(11)：121345.XIAOZY,LIUG,JIANGX,etal.Numericalsimulationmethodsfor2DOFcoupledoscillationsofaircraftJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):121345.

(責任編輯：李明敏)