歐拉不等式的一個加強的改進及其類似
2017-12-24 11:28:46王圣
數(shù)學通報
2017年2期
關鍵詞:探究
王 圣
(安徽滁州中學 239000)
設△ABC的三邊為a,b,c,外接圓和內(nèi)切圓半徑分別為R,r,則有不等式R≥2r.上述不等式是數(shù)學家歐拉于1765年建立,該不等式具有簡單而不平凡的特點,關于它的各種加強、隔離和推廣的研究從未間斷過. 文[1]給出歐拉不等式與邊長間的一個不等式鏈,文[2]則建立了歐拉不等式的如下三角形式的加強不等式
定理1設R,r分別為△ABC的外接圓和內(nèi)切圓半徑,則有(Σ表示循環(huán)和)
(1)
當且僅當△ABC為正三角形時取等號.
(2)
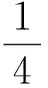
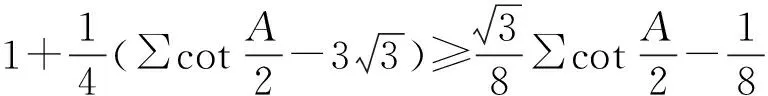
下面給出式(2)的證明.
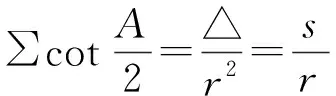
由于
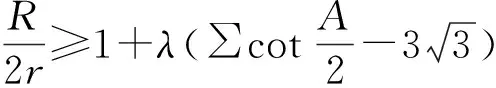
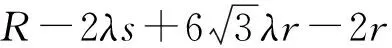
原本到此,對式(1)的探究可以暫告一個段落了,但是數(shù)學大師波利亞告誡我們:“沒有一道題目可以解決得十全十美,總存在值得我們探究的地方”,那么式(1)是否還有東西可以進一步的挖掘?
定理2設R,r分別為△ABC的外接圓和內(nèi)切圓半徑,則有

(3)
當且僅當△ABC為正三角形時取等號.
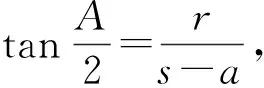
登錄APP查看全文
猜你喜歡
中國交通信息化(2023年11期)2023-12-26 07:43:50
中學生數(shù)理化·高三版(2023年1期)2023-09-04 09:24:31
中等數(shù)學(2021年11期)2021-02-12 05:11:46
今日農(nóng)業(yè)(2019年14期)2019-09-18 01:21:42
快樂語文(2018年13期)2018-06-11 01:18:16
中等數(shù)學(2018年11期)2018-02-16 07:47:42
中學數(shù)學雜志(初中版)(2016年4期)2016-10-08 09:21:22
中國中醫(yī)藥現(xiàn)代遠程教育(2014年13期)2014-03-01 04:26:39

