數學問題解答

2017年10月號問題解答

(解答由問題提供人給出)

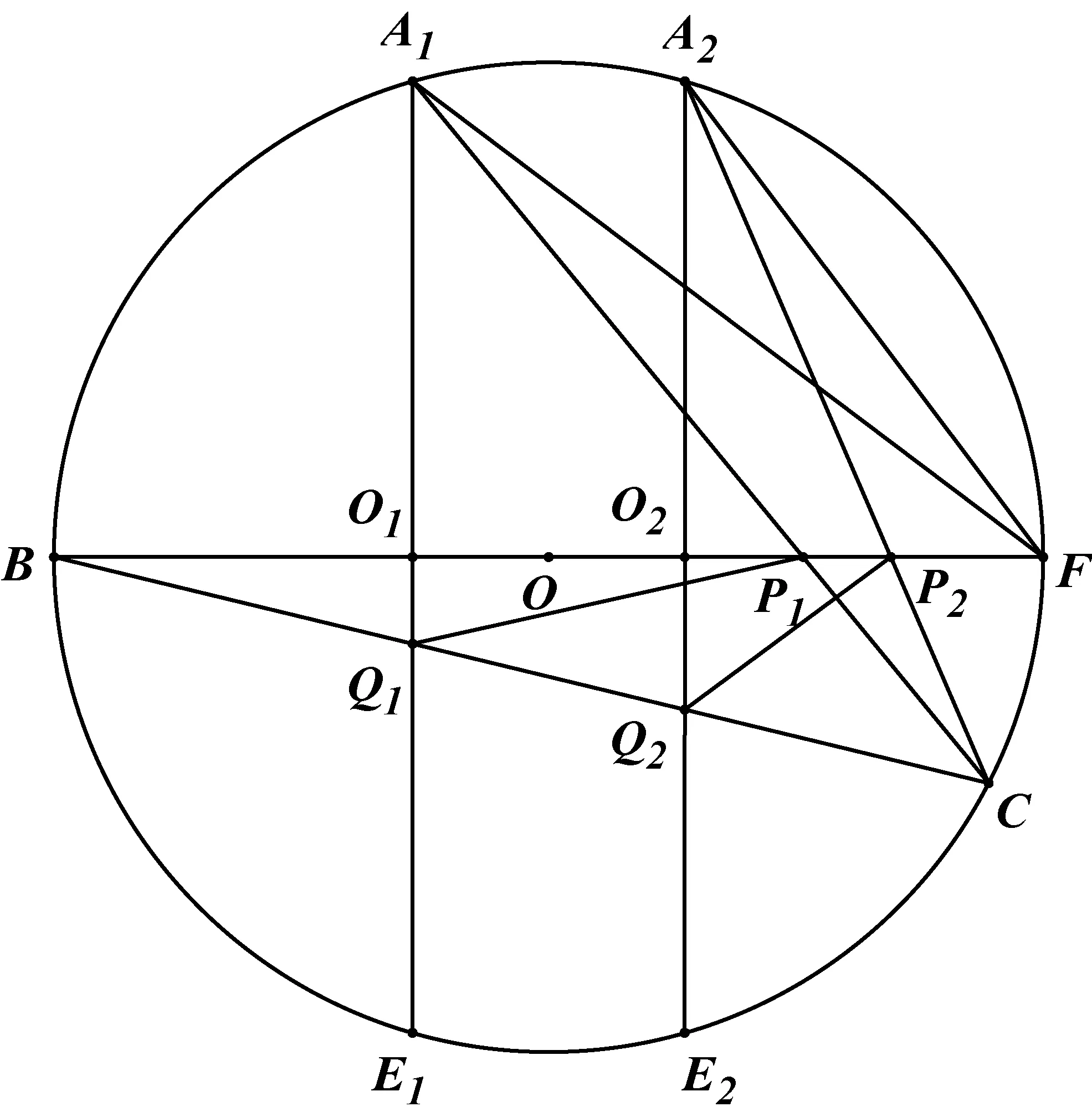
求證：S△BP1Q1·S△BP2Q2=S△FA1P1·S△FA2P2．

(北京市陳經綸中學 張留杰 100020)

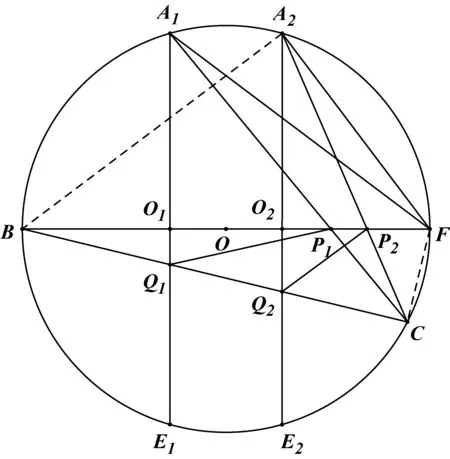
證明如圖，連結CF，

因為A1E1∥A2E2，A1E1=A2E2，

又直徑BF⊥A1E1于O1，

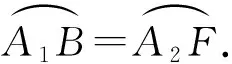
所以∠BCA1=∠FCA2，即∠BCP1=∠FCP2，

∠BCA2=∠FCA1，即∠BCP2=∠FCP1．

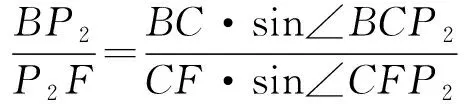
②

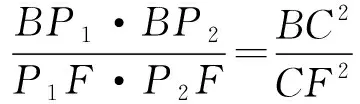
③

因為BF為圓O的直徑，所以 ∠BCF=90°，

所以 Rt△BO1Q1～Rt△BCF，

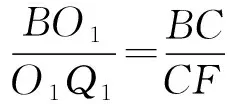
④

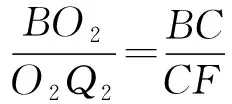
⑤

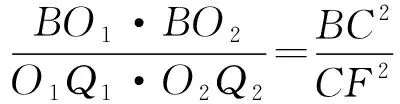
⑥

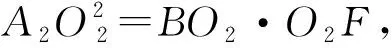
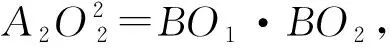
又A1O1=A2O2，

所以A1O1·A2O2=BO1·BO2．

由③和⑥式得

所以(BP1·O1Q1)·(BP2·O2Q2)

=(A1O1·P1F)·(A2O2·P2F)

即S△BP1Q1·S△BP2Q2=S△FA1P1·S△FA2P2．

2387設a,b,c≥0，a+b+c=6，求證：

(陜西省咸陽師范學院基礎教育課程研究中心 安振平 712000 )

證明不妨設a≥b≥c≥0，則2≥c≥0，先考慮

(1)

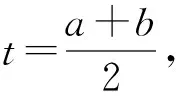
不等式(1)等價于

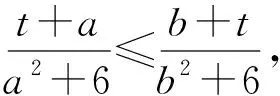
等價于(t+a)(b2+6)≤(b+t)(a2+6)，

等價于6(a-b)≤ab(a-b)+t(a2-b2)，

等價于[(a+b)2+2ab-12](a-b)≥0，

(2)

因為a+b=6-c≥4，

所以(a+b)2+2ab-12≥42+2ab-12>0，

而a≥b，即(2)成立，也就是(1)成立.

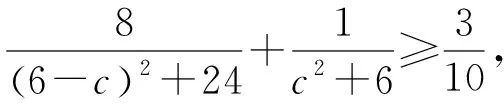
(3)

其中2≥c≥0.

不等式(3)等價于

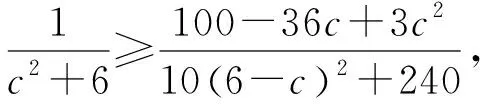
等價于 10(6-c)2+240

≥(c2+6)(100-36c+3c2)，

等價于c4-12c3+36c2-32c≤0，

等價于c(c-2)2(c-8)≤0，

(4)

注意到2≥c≥0，立即知(4)成立.

從以上證明過程，容易知道：當a,b,c都為2，或者a,b,c中一個為0，另兩個為3時，所證不等式取得等號.

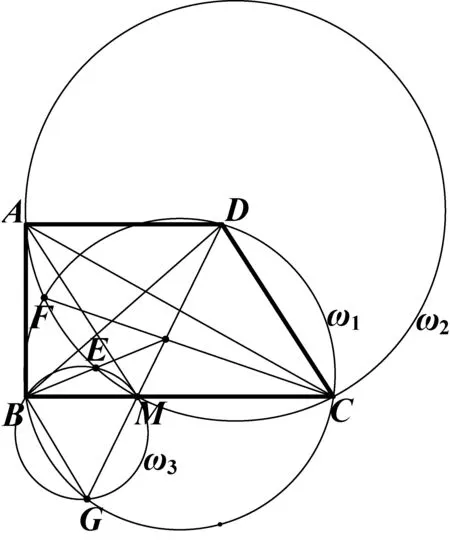
2388如圖，經過直角梯形ABCD的頂點A作斜腰CD的平行線交下底BC于點M，△DBC的外接圓ω1交直線DM于點D,G，△AMC的外接圓ω2交ω1于點C,F，△BGM的外接圓ω3交ω2于點M,E， 證明：直線BE,CF,DG交于一點，且此點為△AMC的重心.

(河南省輝縣市一中 賀基軍 453600)

證明依題意，只須證明直線BE,CF,DG分別過△AMC的重心.

(Ⅰ)如圖，設直角梯形上底AD的延長線與直線BE交于點H.

因∠AMB=∠DCB=∠DGB=∠MGB，

故圓ω3與直線AM相切于點M，

從而有∠EMA=∠EBM=∠EHA，

由此可知A,E,M,H四點共圓，點H在圓ω2上.

因AH∥MC，故圓內接四邊形AMCH為等腰梯形.設它的底邊MC和AH的中點分別為P,Q，

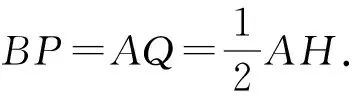
設△AMC的中線AP與直線BH的交點為W，

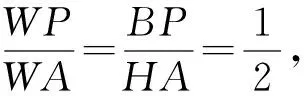
因此W為△AMC的重心，直線BE過點W.

(Ⅱ)在△AMC中，設線段CW的延長線與AM交于點O，并與它的外接圓ω2交于點F′.

作MN⊥AH于點N，則四邊形ABMN為矩形，

點O為對角線AM與NB的交點.

因NB=AM=DC，故四邊形NBCD為等腰梯形(當N與D重合時該圖形為等腰三角形)，它的頂點N,B,C,D共圓，因此點N在圓ω1上.

在圓ω2中，由相交弦定理得

F′O·OC=AO·OM.

因AO·OM=NO·OB，

故F′O·OC=NO·OB，

由此可知F′,B,C,N四點共圓，

點F′在圓ω1上.

這就是說，點F′為圓ω1與ω2的交點，且異于交點C，因此F′,F兩點重合，直線CF過點W.

(Ⅲ)因四邊形AMCD為平行四邊形，故它的對角線MD平分AC，從而可知MD過△AMC的重心W，因此直線DG過點W.