例談用概念解題

孔慶甫

(甘肅省隴南市成縣城關中學 742500)

例談用概念解題

孔慶甫

(甘肅省隴南市成縣城關中學 742500)

初中數學有非常多的基礎性概念，直接影響著學生解題的細節，概念在教材中的呈現作為范本，是教學的重要依據，對概念的理解和靈活使用是正確解題的關鍵，而這正是數學解題中不經意間出現的問題.

相反數；絕對值；概念；解題方法

初中數學有非常多的基礎性概念，直接影響著學生解題的細節，概念在教材中的呈現作為范本，是教學的重要依據，對概念的理解和靈活使用是正確解題的關鍵，而這正是教學解題中不經意間出現的問題.應從以下點滴舉例談起.

點滴一、從讀法上規范對概念的理解以便正確解題

1.用相反數的概念解題

案例1 計算出錯.如:-12=1；-(-1)=-1等.讀法出錯.如:把“-a”讀作負a； 把“-a2”讀成“負a的平方”.

訂正:這兩處錯誤均與相反數的概念有關.單項式中的性質符號“-”表示“相反”的意思.相反數:只有符號不同的兩個數互為相反數.如:a的相反數是-a.故“-a”，應該讀成a的相反數.特別是“-a2”的讀法，也有人讀成“負的a的平方”，根據相反數的意義，應該正確讀成“a的平方的相反數”.以此類推(-a)2可讀為“負a的平方”；-(-a)2讀法為“負a的平方的相反數”;-(-a2)可讀為“a的平方的相反數的相反數”.這種正確的讀法既有概念規則的依據，又有計算順序的陳述,可以杜絕以上案例的錯誤，便于以下計算的正確.

練習1 計算:-12=____； (-1)2=____；-(12)=____；-(-1)2=____.

2.用算術平方根與平方根組合的雙重性解題

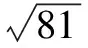
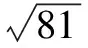
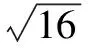
點滴二、從逆反思維上判斷對概念的理解以便正確解題

平方根的性質:一個正數的平方根有兩個，它們互為相反數.

既一個正數的平方根是m和n，那么m和n是一個正數的平方根時有幾種情形

案例3 判斷正誤

9的平方根是3(×)(判斷正數的平方根的個數)

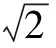
由以上判斷可知:

(1)若m和n是一個正數的平方根,則m和n取值有兩種情況:

可能相等:m=n；

可能互為相反數:m+n=0.

(2)若一個正數的平方根是m和n,則m和n取值只有一種情況:m+n=0

練習3 若一個正數的平方根是2m+3和m+1,求這個正數的值.

解∵一個正數的平方根有兩個，它們互為相反數，

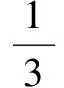
練習4 若2m+3和m+1是一個正數的平方根,求這個正數及m的值.

作為教師應潛心研讀教材并指導學生細心閱讀教材，創造性地整合教材資源，多研究教材內容，把握概念的深度、廣度及對學生的適宜度，利用概念的準確性去正確解題.

作為七年級學生，受年齡和認知的影響，雖然要淡化概念，注重實際操作，但淡化是建立在對概念深度理解的基礎上的，這樣才不至于在思考中偏離方向，模棱兩可.也只有在理解概念的基礎上把握數學中的規則與順序，去杜絕錯誤、糾正錯誤，而這些正是在教學中應該突破的難題.在教學中，把學生推向學習的前沿，讓學生感知教材中的知識點與數學思想方法，區別記憶數學中的規則與計算順序.不怕出錯，即使出錯也要徹底糾錯，糾錯的方法是對錯因要刨根問底，對教材內容的創造性整合，讓學生自主接受理解，清楚錯因，不重復錯誤，以杜絕馬虎現象再次發生.

[1]孫友權.優化復習設計,打造高效的數學復習課堂——以“一次函數復習課”為例[J].數學教學通訊,2015,28:7-9.

[2]猶大維.淺談一次函數的復習[J].數學學習與研究,2014,04:18.

2017-07-01

孔慶甫(1966.10-)男，漢族，甘肅成縣人，本科，中學一級教師，從事初中數學教法.

G632

A

1008-0333(2017)32-0024-02

李克柏]