基于ANSYS的噴涂機器人擺桿模態分析

占曉煌 ，陳潤六 ，鄒曉暉 ，鄭小民 ，王紅州 ，張志勇

（1.江西制造職業技術學院，江西 南昌 330095；2.江西省機械科學研究所，江西 南昌 330002）

基于ANSYS的噴涂機器人擺桿模態分析

占曉煌1，2，陳潤六1，2，鄒曉暉1，2，鄭小民1，2，王紅州1，2，張志勇1

（1.江西制造職業技術學院，江西 南昌 330095；2.江西省機械科學研究所，江西 南昌 330002）

本文以噴涂機器人的擺桿為研究對象，利用SolidWork建立了幾何模型，將擺桿模型保存為Parasolid格式并導入到ANSYS有限元分析軟件。對噴涂機器人擺桿的結構進行了有限元模態分析，獲得了噴涂機器人擺桿前10階的固有頻率。并通過臨界轉速計算公式獲得了臨界轉速，驗證了噴涂機器人擺桿的結構設計能夠滿足使用要求。為其下一步進行優化設計提供了理論依據，有利于提高噴涂機器人的可靠性與壽命。

模態分析；固有頻率；ANSYS

機械振動是機械系統在其平衡位置附近的往復運動。振動會降低機械動態進度和使用性能。共振是工程中重要的概念，它在激振力頻率與系統固有頻率接近時發生，所以計算振動系統的固有頻率或臨界轉速具有重要意義。

擺桿是噴涂機器人的核心功能部件，噴涂機器人工作時，其擺桿在運轉過程中會受到各種作用力的影響，如果擺桿發生強烈振動，噴涂機器人的工作精度、可靠性以及壽命會受到很大影響。

為了驗證噴涂機器人擺桿的結構是否具有合理性，尤其是在工作時是否會發生共振情況，因此，必須對其進行模態分析。本文運用三維軟件SolidWorks和有限元軟件A NS Y S對噴涂機器人擺桿進行模態分析，根據分析的結果提出優化策略。本研究對實現動態特性優化和指導實際生產都具有重要意義。

1 噴涂機器人擺桿有限元模型的建立

考慮到噴涂機器人擺桿結構復雜，選擇軟件SolidWorks進行建模。并對模型進行了合理的簡化處理：（1）將擺桿模型中的小圓角、小倒角和退刀槽等特征去除；（2）忽略因焊接造成零件本身的彎曲剛度等影響。利用Solidworks建立出該擺桿的三維幾何模型，如圖1所示。然后將擺桿模型輸出為Parasolid格式并導入到有限元分析軟件A NS Y S中。而后將導入的模型進行修復以形成幾何實體模型。建立有限元模型還必須對單元類型、材料屬性、網格劃分等設置。設置有限元模型單元為Solid45，材料屬性設置參數如表1所示。

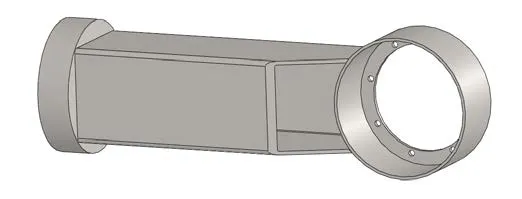
圖1 實體模型

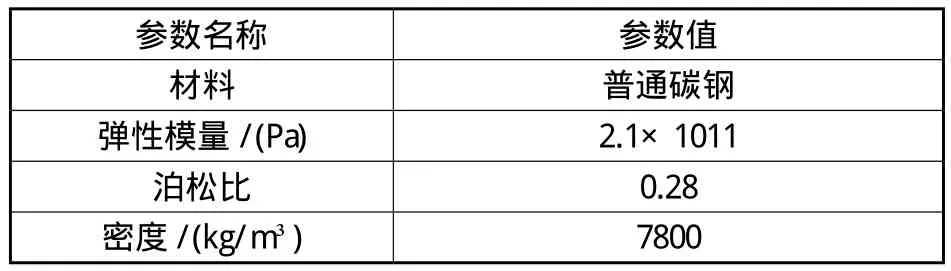
表1 擺桿參數

網格劃分產生的單元數量直接影響計算量和計算精度，由于模型結構復雜因此采用自由(F r e e)網格劃分，取劃分大小為5 mm。共劃分生成實體單元47947個，節點15953個，得到如圖2所示的實體單元的有限元模型。

圖2 有限元模型

2 噴涂機器人擺桿的模態分析

根據機械振動力學可知，擺桿的振型是由所有階次的固有振型進行相加而成的，并且對整個結構的振動特性起主導作用的前幾階次的固有振型決定了整個結構的振動特性基本上也是前幾階有振型。由于擺桿的低階模態才對擺桿的振動分析有實際的參考價值，故此次模態分析只計算擺桿的前10階固有頻率。

模型的約束方式不同，對模態分析產生的結果也不同，邊界條件發生變化，產生的的模態也會發生變化。針對噴涂機器人實際運行情況，采取對擺桿端面施加固定約束。

通過A NS Y S定義噴涂機器人擺桿的定義邊界條件、設定模態分析項和分析求解，最后得到擺桿前10階固有頻率結果如表2所示。

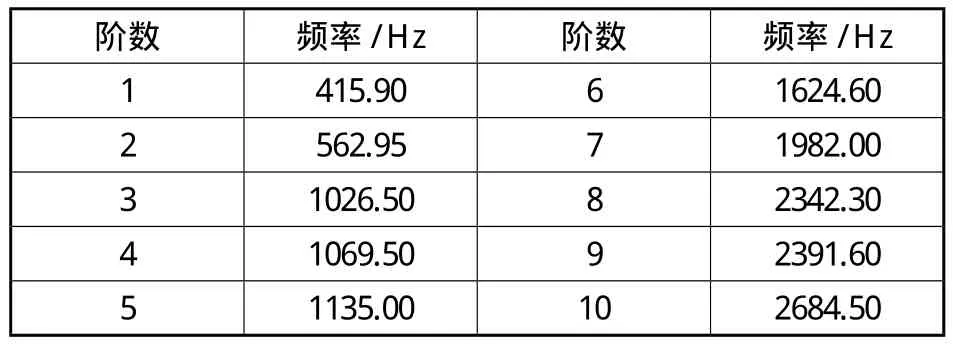
表2 擺桿前10階固有頻率

3 噴涂機器人擺桿的臨界轉速

若噴涂機器人在工作時，運轉速度不斷提高到達一定速度后就會逐漸出現振動現象，并在某一轉速達到共振，則這個轉速稱為臨界轉速。機器人短時間在臨界轉速下運轉會導致機器人噴涂精度發生偏差，若長時間在臨界轉速運轉則會使得擺桿疲勞加速和使用壽命縮短。

在實際工作條件下，影響噴涂機器人的臨界轉速因素多種多樣，例如擺桿結構尺寸、材料屬性、預緊方式和使用環境等。根據擺桿的使用要求和結合具體噴涂機器人的結構特點建立簡化模型。噴涂機器人擺桿的臨界轉速和頻率的關系可以簡化為：

式中，N為臨界轉速（r/mi n）；f為頻率（Hz）。

將A NS Y S分析所獲得的擺桿前10階固有頻率代入式（1），得到擺桿前10階固有頻率所對應的臨界轉速。擺桿的一階固有頻率值為415.90 Hz，對應的臨界轉速為24954 r/mi n。為了確保噴涂機器人擺桿工作時具有可靠的精度，擺桿運轉時的轉速必須低于該擺桿一階臨界轉速的75%。

噴涂機器人實際運行最高轉速為2000 r/mi n，與該擺桿的一階臨界轉速24954 r/mi n進行比對，可明顯得知該擺桿工作時最高轉速都遠低于計算得出的一階固有頻率對應的臨界轉速的75%。而一階以后各階固有頻率對應的臨界轉速更高，所以可以得出該擺桿在工作運轉過程中不會出現共振現象，可以保證該噴涂機器人的可靠性和精度。

4 結語

（1）本文采用SolidWorks三維設計軟件建立了擺桿的幾何模型，再將幾何模型導入A NS Y S分析軟件中進行網格劃分，得到了擺桿的有限元模型。

（2）通過自由振動方程求得擺桿的模態矩陣，并通過A NS Y S對擺桿進行模態分析，得出其前10階固有頻率。

（3）根據臨界轉速與頻率簡化公式，計算得到該擺桿前10階固有頻率的臨界轉速。擺桿運轉時的轉速低于該擺桿一階臨界轉速的75%。得出該擺桿在工作運轉過程中不會出現共振現象，可以保證該噴涂機器人的可靠性和精度。

（4）本文建立的噴涂機器人擺桿模型、有限元模型和模態分析結果，可為該擺桿后續進行結構優化設計提供支撐數據。

[1]劉釗，秦仙蓉，朱傳敏.機械振動[M].上海：同濟大學出版社,2016.

[2]蔡泰信，和興鎖.理論力學教與學[M].北京:高等教育出版社,2007.

[3]張小安. 礦用車變速器傳動斜齒圓柱齒輪有限元分析[J].煤礦機械,2017,(07).

[4]韓騰. 基于ANSYS Workbench的磨床主軸模態分析[J].機電信息,2017,(12).

[5]成大先. 機械設計手冊（第4版）[M].北京:化學工業出版社,2008.

TP242；TP273

：A

：1671-0711（2017）12（下）-0086-02

江西省教育廳重點課題：基于觸摸屏和P MA C的噴涂機器人控制系統研究（項目編號：G J J 151484）。