行為AANA陣列的若干收斂性

王寬程

(閩南理工學院信息管理學院,福建 泉州 362700)

行為AANA陣列的若干收斂性

王寬程

(閩南理工學院信息管理學院,福建 泉州 362700)

在較廣泛的條件下，研究了AANA陣列行和的收斂性質，利用截尾方法和矩不等式,獲得了行為AANA陣列的弱大數律、Lp收斂性和完全收斂性定理,所得結果推廣了前人的相應結果.

AANA陣列;收斂性;一致可積

1 引言

稱{Xn;n∈N}為漸近幾乎負相依(簡稱AANA)隨機變量序列,如果存在非負序列

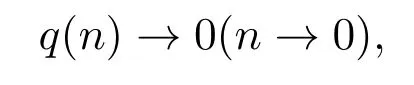
對任意的n,k≥1都有

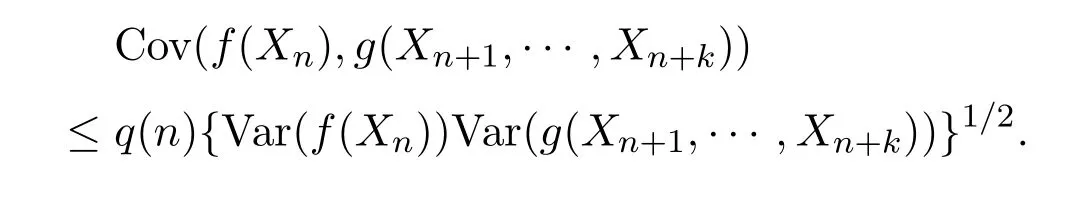
其中f和g是任何兩個使上述方差存在且對每個變元均為非降的連續函數.稱{q(n);n∈N}為該序列的混合系數.

AANA序列是包含NA列(令q(n)=0,n≥1)和獨立列的更廣泛的隨機變量序列.顯然,如果隨機變量序列是NA列,則一定是AANA列,反之不然[1].此外,AANA序列也不同于ANA列[2].近年來有關AANA序列的研究,已取得不少的成果,可以參考文獻[3-7].但對于AANA隨機陣列的研究比較少,本文研究AANA陣列行和的若干收斂性質.

稱隨機陣列{Xni;1≤i≤n,n∈N}是行為AANA陣列,固定n,假設每一行內的隨機變量列{Xni}是AANA的.

本文主要研究形如

的行和的最大值的弱大數率、Lp收斂性和完全收斂性.推廣和改進了NA列和獨立情形的大數定律和完全收斂性[8].

稱隨機陣列{Xni;1≤i≤n,n∈N}是p階cesaro一致可積的,若

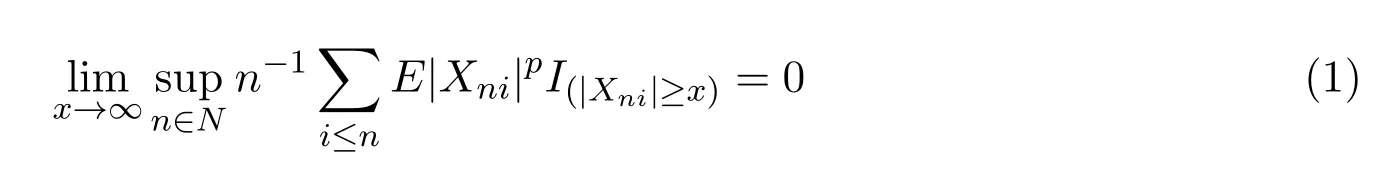
顯然p階一致可積蘊含p階cesaro一致可積的,但反之不成立,即p階cesaro一致可積嚴格弱于p階一致可積[9].

本文一律用C表示與n無關的正常數,并且C可在不同的地方表示不同的常數.

2 主要結果與證明

引理 2.1[1]設{Xn;n∈N}為AANA序列,并且混合系數是{q(n);n∈N},若{fn;n∈N}皆是單調非降(或者單調非增)連續函數,那么{fn(xn);n∈N}仍然是AANA序列,其混合系數仍然是{q(n);n∈N}.

引理 2.2[4]設{Xn;n∈N}是均值為0的AANA序列,混合系數{q(n);n∈N},1＜p≤2,那么存在僅依賴于p的正數Cp,使得

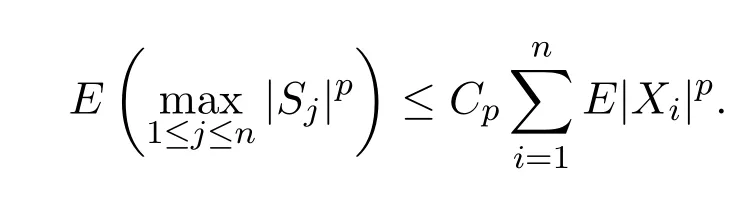
定理 2.1設{Xni;1≤i≤n,n∈N}是行為AANA陣列,其混合系數q(n),n≥1,可以滿足

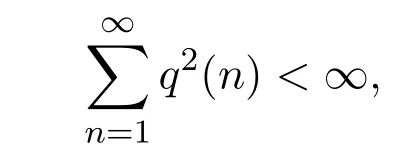
且對1＜p＜2,有

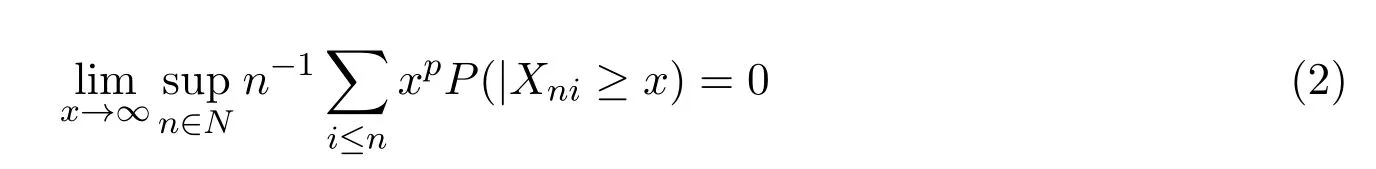
則

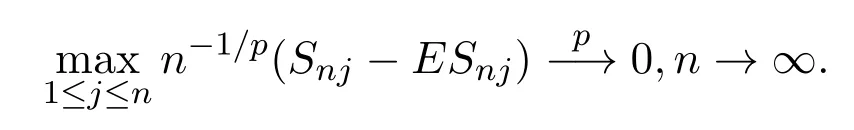
定理 2.1的證明取xn=n1/p,當n→∞時,xn→∞,對Xni截尾,記

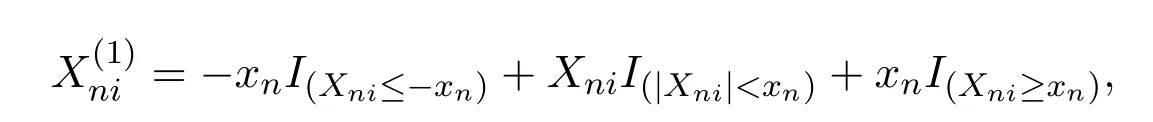
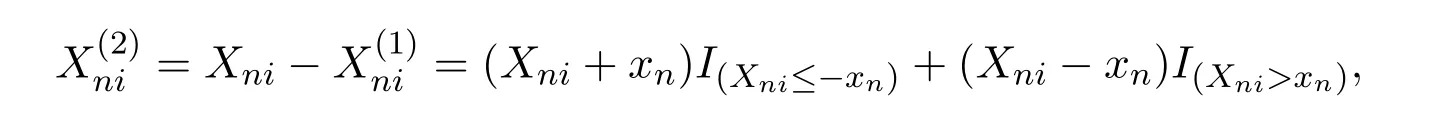
當1＜p＜2時，由引理2.1知,

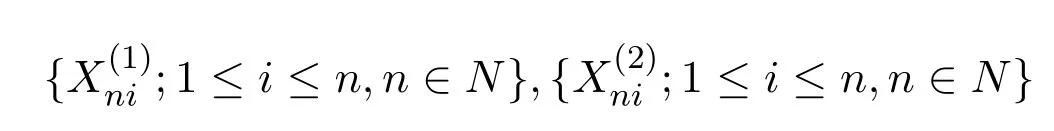
仍是AANA陣列,因

要證定理2.1,只需證Jn1→0,Jn2→0,n→0.由引理2.2以及Morkov不等式可得

由 (2)式,且xn=n1/p得,

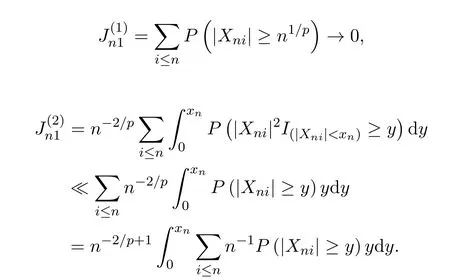
由 (2)式,?ε＞0,?M,使當y＞M時有

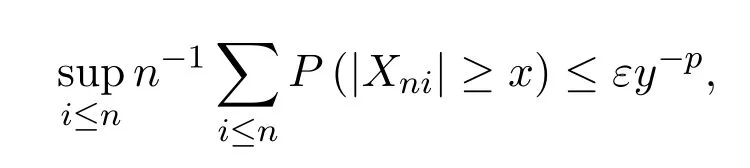
即以當xn＞M時,有

由1＜p＜2,以及ε的任意性得,n→∞.

下證Jn2→0,n→∞,由的定義及(2),有

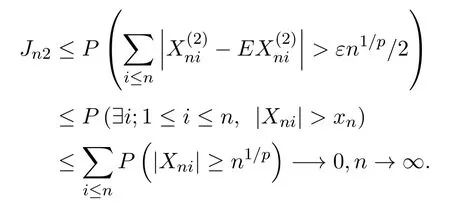
定理2.1證明完畢.

推論 2.1設{Xn;n≥1}是NA列,且對1＜p＜2,有

則

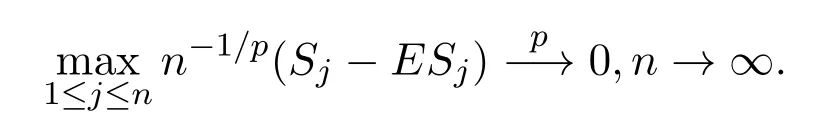
證明由

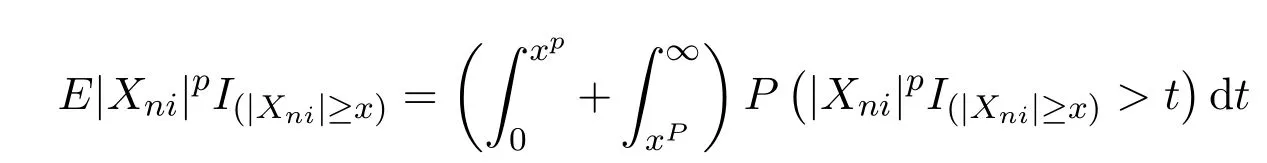
知,(1)式等價于(2)式，也等價于(3)式.再由定理1可得證.

特別取{Xn;n≥1}為同分布NA列,則(3)變為

這一結果推廣了文獻[10]的定理1的充分結果,因此,定理2.1把NA列的相關結果推廣到了AANA陣列.

定理 2.2設{Xni;1≤i≤n,n∈N}是行為AANA陣列,其混合系數q(n),滿足

且對1＜p≤2,有(1)式成立,則

定理 2.2的證明仍用定理2.1的記號,這里取xn=n(1?p/2)/4,因1＜p≤2,當n→∞時,xn→∞,由Jessen不等式,引理2得

定理2.2證明完畢.

推論 2.2設{Xn;n≥1}是NA列,且對1＜p＜2,有

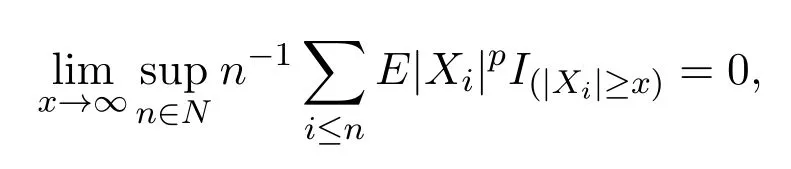
則

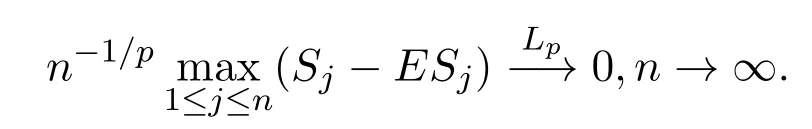
定理 2.3設{Xni;1≤i≤n,n∈N}是行為AANA陣列,其混合系數q(n),滿足

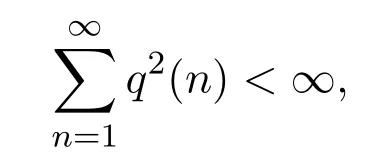
且對1＜p≤2及δ＞1時,滿足

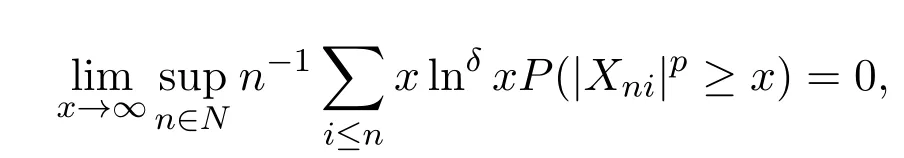
則對αp≥1有

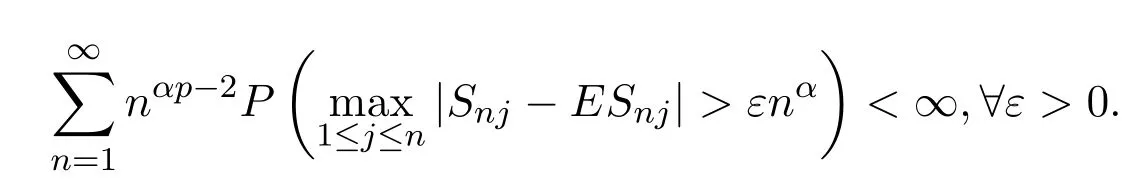
定理 2.3的證明仍沿用定理 2.1的記號,取xn=nα(2?p)/4,?ε＞0有

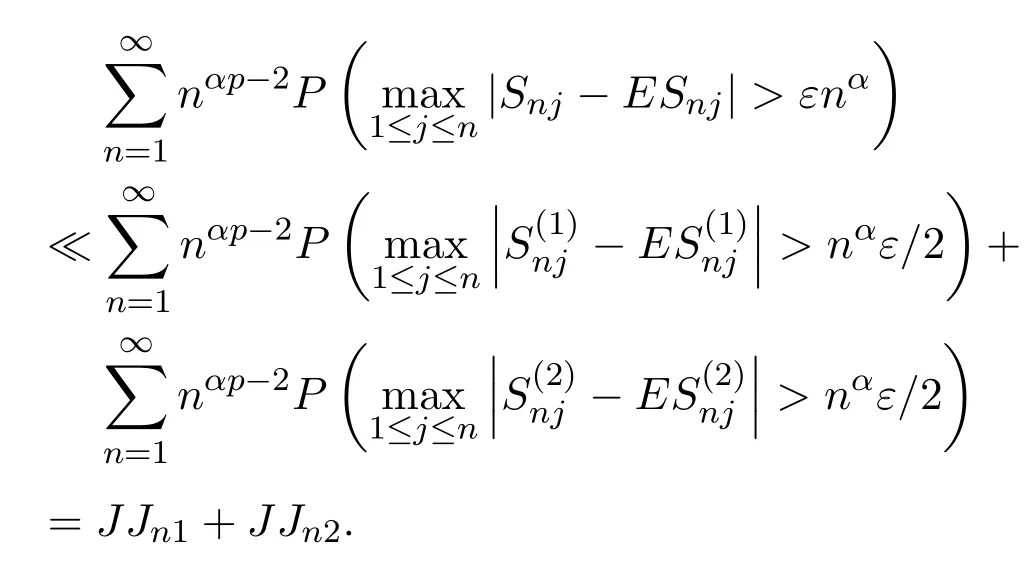
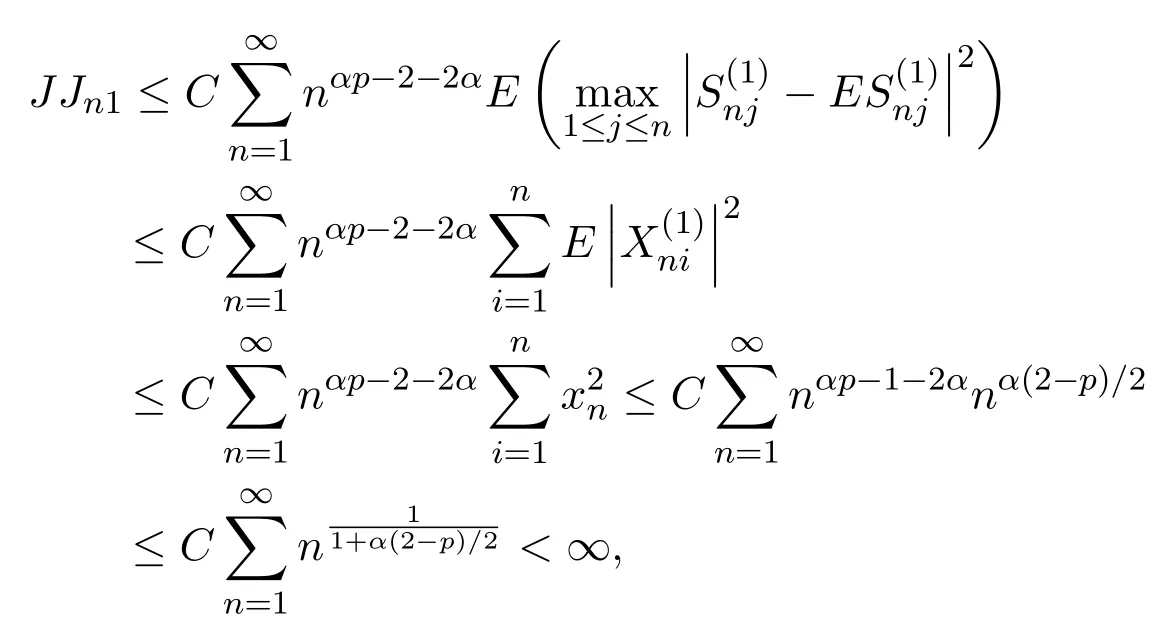
由

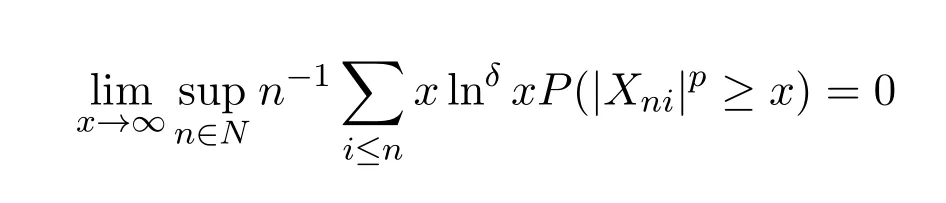
知,?M＞0,當x＞M時,有

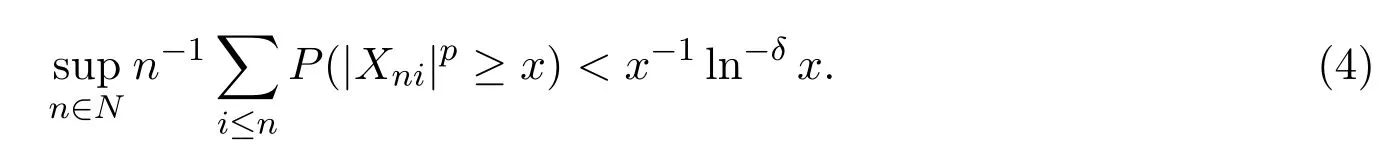
又因為xn=nα(2?p)/4,所以?N＞0,使得當n＞N時,有xn＞M,則

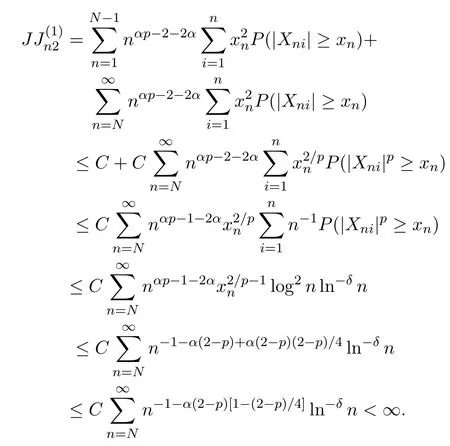
同理可得

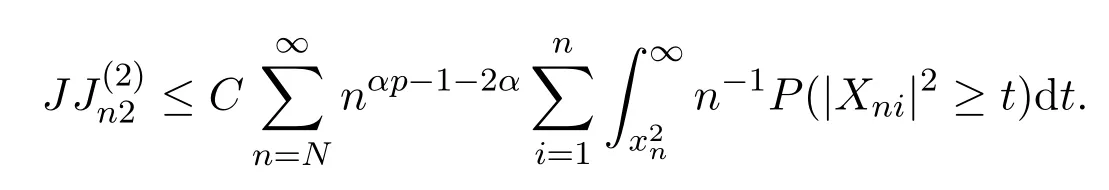
令t=z2/p,則有

由(4)得

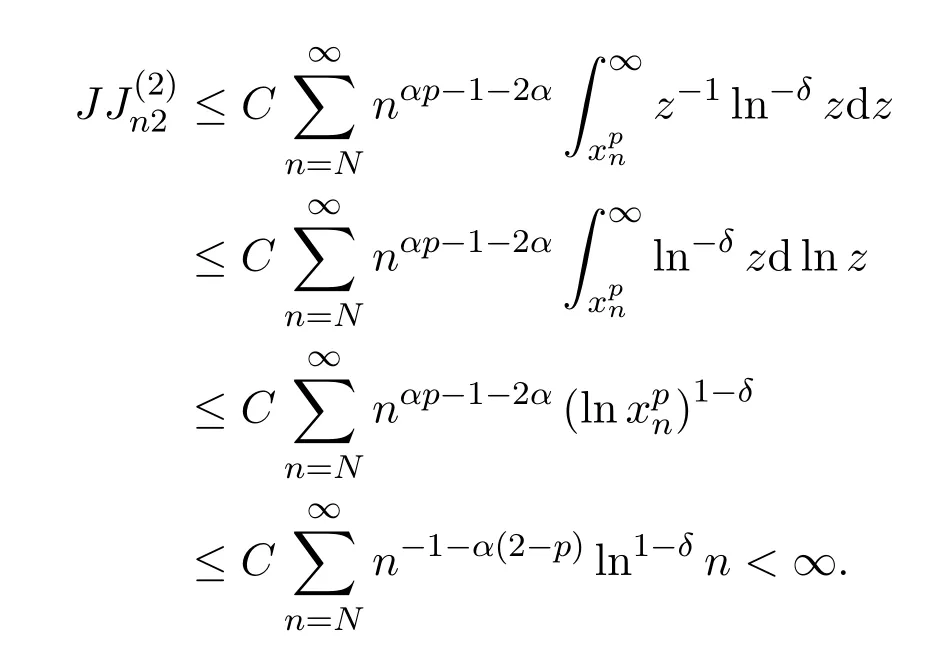
推論 2.3設{Xn;n≥1}是NA列,且對1＜p＜2有

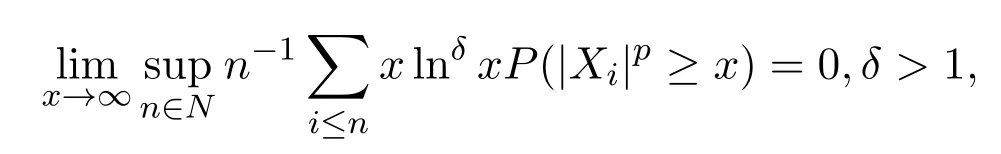
則對αp≥1,有

[1]Chandra T K,Ghosal S.Extensions of the strong law of number of Marcinkiewicz and Zygmund for dependent variables[J].Acta Mathematical Hungarica,1996,71(4):327-336.

[2]Zhang L X,Wang X Y.Convergence rates in the strong laws of asymptotically negatively associated random fields[J].Appl.Math.J.Chinese Univ.Ser.B,1999,14(4):406-416.

[3]Ko M H,Kim T S,Lin Z.The Hajek-Renyi inequality for the AANA random variables and its applications[J].Taiwanese Journal of Mathematics,2005,9(1):111-122.

[4]Yuan D M.An J.Rosenthal type inequalities for asymptotically almost negatively associated random variables and applications[J].Sci.China Ser.A,2009,52(9):1887-1904.

[5]Wang X J,Hu S H,Yang W Z.Convergence properties for asymptotically almost negative associated sequence[J/OL].Discrete Dynamics in Nature and Society,2010,http://dx.doi.org/10.1155/2010/218380.

[6]Wang X J,Hu S H,Li X Q,et al.Maximal inequalities and strong law of large numbers for AANA sequences[J].Communications of Korean Mathematical Society,2011,26:151-161.

[7]Wang X J,Hu S H,Yang W Z.Complete convergence for arrays of rowwise asymptotically almost negatively associated random variables[J].Discrete Dynt.Soc.,2011,2011:11.

[8]萬成高.鞅的極限理論[M].北京:科學出版社,2002.

[9]Chandra T K.Uniform integrability in the Cesaro sense and the week law of large numbers[J].the Indian Yournal of Siatistics(series A),1989,51:309-317.

[10]遲翔,蘇淳.同分布NA序列的一個弱大數律[J].應用概率統計,1997,13(2):199-203.

Some convergence properties of arrays of rowwise AANA random variables

Wang Kuancheng
(Minnan University of Science and Technology,Quanzhou 362700,China)

Under very mild conditions,the convergence properties for the sums of rowwise asymptotically almost negative associated random variables.By the truncated method and the means moment inequality,the author is able to give the week law of large numbers,Lp convergence and complete convergence of rowwise asymptotically almost negative associated random variables.The results extend the corresponding results in series of previous papers.

arrays of AANA,convergence properties,uniformly integral

2017 MSC:12M06

O211.4

A

1008-5513(2017)06-0615-08

10.3969/j.issn.1008-5513.2017.06.007

2017-10-07.

福建省中青年教師教育科研項目(JAT170739).

王寬程(1981-),碩士,講師,研究方向：概率極限理論.