廣義典型流形上連續小波變換的性質

周小輝 顧桂定王剛

(1.上海財經大學數學學院,上海 200433;2.浙江財經大學東方學院,浙江 嘉興 314408;3.新疆師范大學數學科學學院,新疆 烏魯木齊 830054)

廣義典型流形上連續小波變換的性質

周小輝1,2, 顧桂定1,王剛3

(1.上海財經大學數學學院,上海 200433;2.浙江財經大學東方學院,浙江 嘉興 314408;3.新疆師范大學數學科學學院,新疆 烏魯木齊 830054)

研究廣義典型流形M上小波變換的性質,根據廣義典型流形M的結構特征與廣義典型流形M上連續小波變換的定義,討論了廣義典型流形M上的連續小波變換的重構公式,線性性質,伸縮平移性等,討論了廣義典型流形M上小波變換的性質.最后,給出了連續小波ψ的卷積公式.

廣義典型流形;連續小波變換;一般線性群GL(V)

1 引言

近年來,很多學者對小波分析的發展都做出了許多突出的貢獻.應用范圍不斷擴展,理論層次不斷提高[1-18].值得注意的是,在許多領域,“流形上小波”的研究已經成為一個研究方向和研究趨勢.許多學者試圖基于“平直空間”的小波分析理論去建立與發展流形上的小波分析[13,18].人們所研究的流形上的小波理論已經牽涉到各種各樣的光滑流形,例如,雙葉雙曲面,拋物面[12-13,18]或是其他二維光滑流形;還有一些抽象流形[16-17].流形上小波的研究不論是局部的還是整體的,這些成果都是有意義的.研究某些流行上的小波理論,人們常常采用以下一些方法,例如,基于一些“好”的性質的投影（保面積投影,徑向投影,球極平面投影）將傳統的小波理論提升到流形M上,或者基于某些流形具備良好的結構與性質來討論小波分析.本文在流形上的小波理論方面也做了一些工作,包括一些光滑曲面和抽象流形,例如,旋轉類光滑曲面,某些可展曲面[18],廣義典型流形[17]等等.

本文將專注于討論廣義典型流形M上的連續小波變換的性質,如,重構公式,線性性質,伸縮平移性等等.

2 預備知識

為了討論廣義典型流形M上小波分析,首先給出廣義典型流形的定義,進一步給出相應的小波理論.下面,逐步給出與廣義典型流形和小波理論相關的若干定義.

定義 2.1[3,17]如果在F域上一個向量空間V中所有可逆線性變換在乘法運算下構成一個群,那么這個群稱為一般線性群,記作GL(V).

例如,酉群、正交群,這類群稱為典型群.關于典型群的概念,可以參見文獻[4,7].一個流形結合典型群的結構,便生成了典型流形.

定義 2.2[4](典型流形)假設M是一個微分流形,且M是一個可逆典型群G.如果存在從乘積流形G×G到G的映射,即

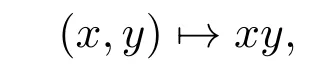
且從G到G的映射,即

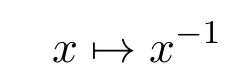
是C∞,那么稱微分流形M和典型群G是一致的(相容的),當微分流形M=G的流形結構與群結構是一致的(相容的),我們稱M(G)是典型流形.

下面有必要給出拓撲群上Fourier變換的一些符號和性質.

定義2.3[5-6]設G是一個局部緊的可換的Hausdorff拓撲群.且?G是其對偶群,χ∈?G是G的一個連續特征,μ是G上的Haar測度.?f∈L1(G),定義f的Fourier變換如下：

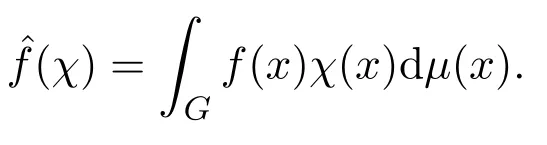
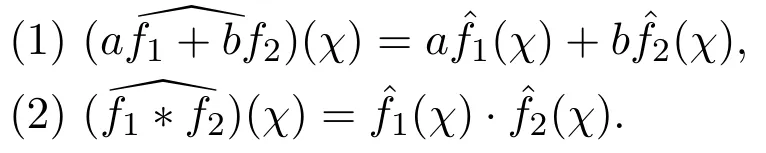
其中f1?f2表示G上函數f1和f2的卷積.在定義3.1中,給出了卷積的定義,同時在定理3.4中驗證了性質(2).

引理2.1[17]設P是在空間

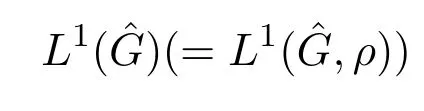
中由正定函數生成的子空間,則存在逆變換公式：

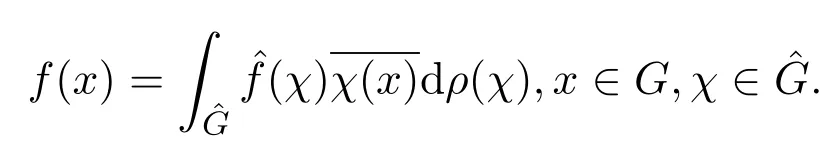
引理 2.2[17]設f,g∈L2(G)則有

從引理2.2中,可以得到Hilbert空間L2(G)的內積的定義,以及一個重要等式.同時根據Hilbert空間L2(G)的內積及Cauchy-Schwarz不等式,則有

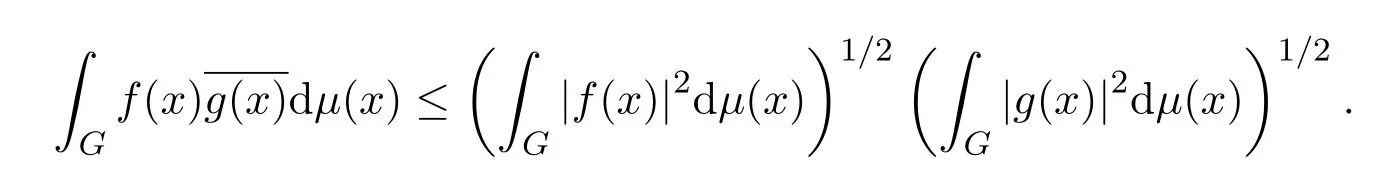
定義 2.4[17](廣義典型流形或拓撲域流形) 假設M是一個微分流形,且M也是一個拓撲域G.微分流形M=G與拓撲域G=M是一致的(相容的).如果關于流形G的C∞結構的加法與乘法運算都是C∞的,我們稱拓撲域M是拓撲域流形(TF-流形或廣義典型流形).

關于廣義典型流形的實例可參見文獻[14].

定義 2.5[17]假設G是一個域,局部緊拓撲群(G,+)上右Haar測度用μ來表示,E是G的可測子集,且令

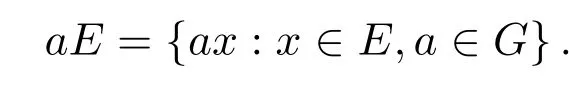
設Δ(a)是G上的非負連續函數.如果?a∈G,有

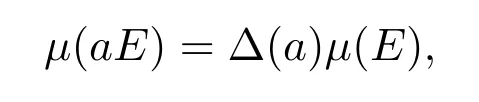
那么μ稱為域G上的Haar測度,且Δ(a)稱為局部緊拓撲群(G,+)上右模函數.

定義2.6[17]對于

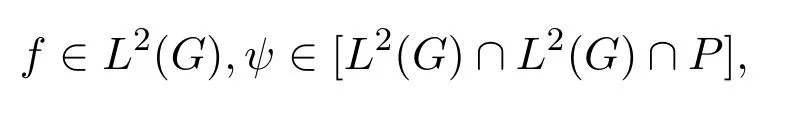
定義函數f的連續小波變換為:

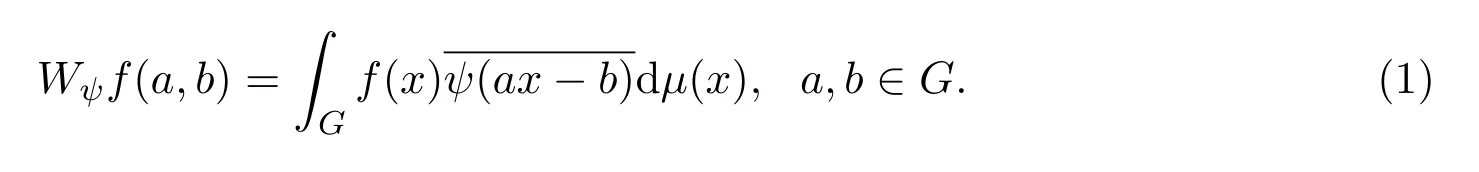
在?G上對G的作用,我們定義為:如果a∈G,χ∈?G,在χ上對a的作用定義為a·χ∈?G,(a·χ)(x)=χ(ax),a,x∈G.特別地,

3 廣義典型流形上連續小波變換的性質

在文獻[17]中,通過計算ψ(ax?b)的Fourier變換,得到

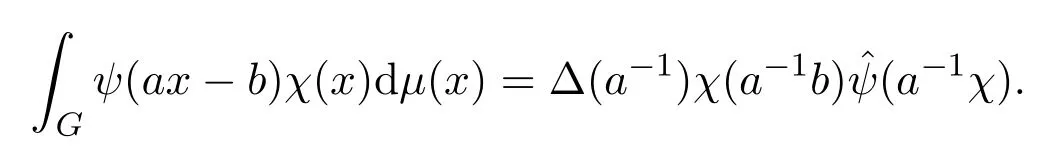
進一步給出了下面引理.

引理3.1[17]如果

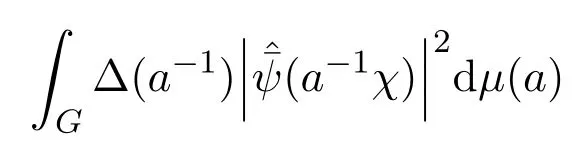
是一個有限常數N,那么

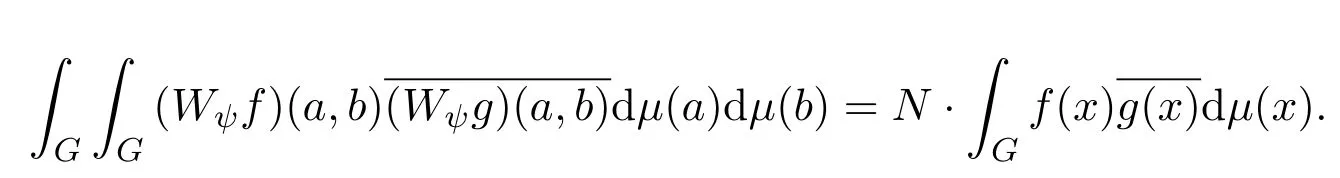
通過計算,

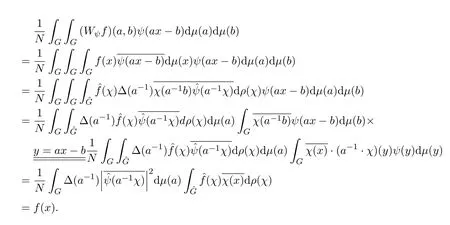
可得下面的定理：

定理3.1如果

是一個有限的常數N,小波變換的逆變換(重構公式)是

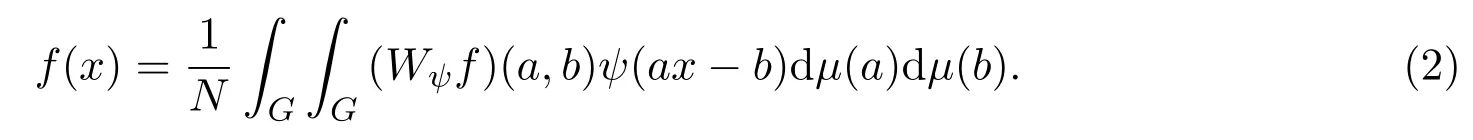
小波函數的性質對于連續小波變換是非常重要的[12].然而,廣義典型流形上的連續小波同樣繼承傳統小波的線性性質,伸縮和平移性質.相關的定理給出如下：

定理 3.2[5]假設,那么

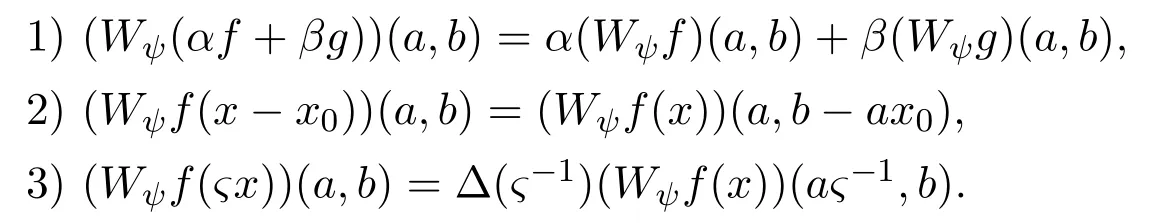
證明根據廣義典型流形上連續小波變換的定義,即(1)式可知,

這就證明了線性性質1).類似的可以證明平移性質2)和伸縮性質3).

定理 3.3假設f,g,?,ψ∈[L1(G)∩L2(G)∩P],α,β ∈R,?∈G,那么

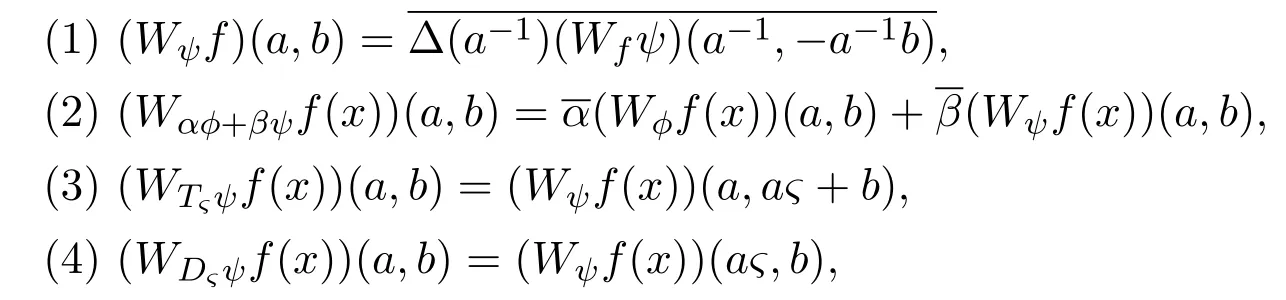
其中平移算子

伸縮算子

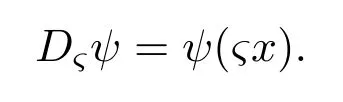
證明

類似地,可以證明其他等式.

定義 3.1假設f,g∈L2(G),x,y∈G,在G上函數f和g的卷積定義如下：

定理 3.4[5]假設f,g∈L2(G),x,y∈G,在G上函數f和g的卷積滿足下面的等式：

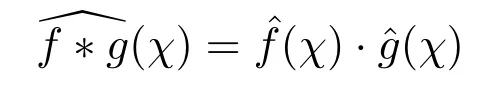
證明根據Fourier變換的定義,

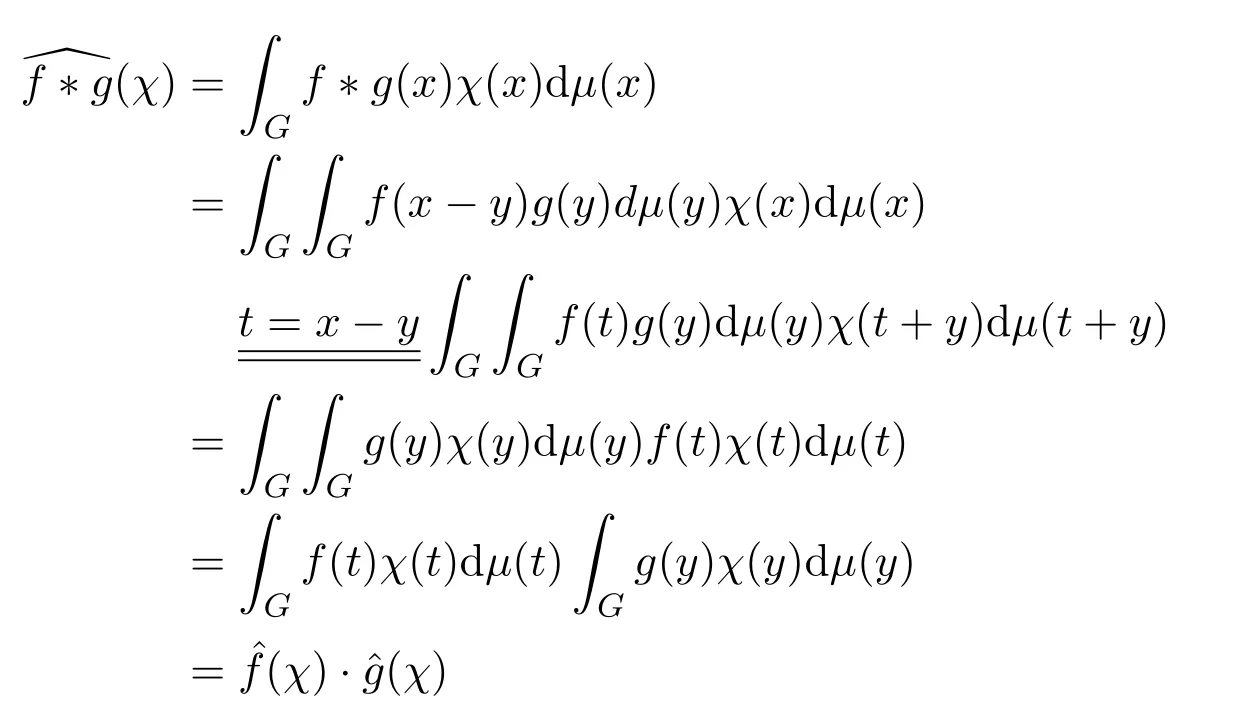
因此,G上函數f的小波變換可以看成是函數f與的卷積,即

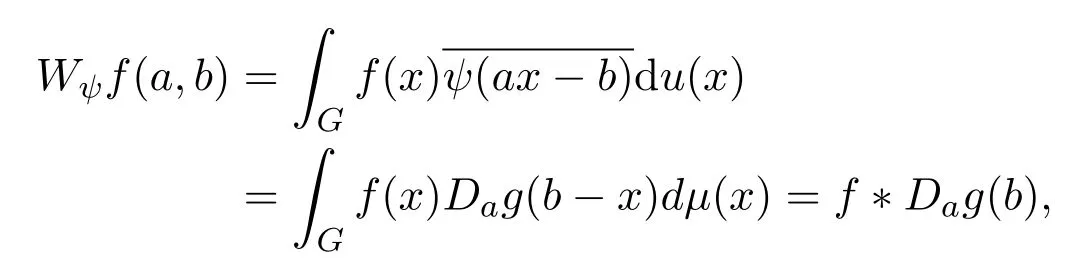
其中a,b∈G.

定理3.5假設

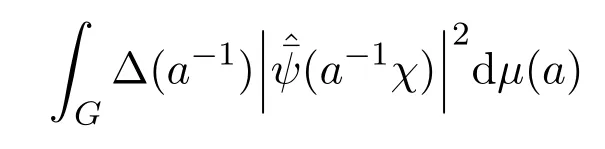
是一個有限常數N,ψ∈L2(G),且?在廣義典型流形G上是有界的且可積的,那么ψ??∈L2(G)且

也是一個有限的常數.

證明因為ψ∈L2(G),?是有界的且可積的,那么

則ψ??∈L2(G).進一步,

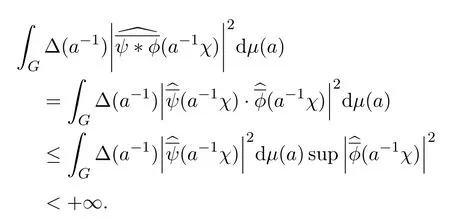
定理得證.

4 結論

根據廣義典型流形M的獨特結構,我們可以定義M上的連續小波變換且存在相應的逆變換(重構公式).進一步,在廣義典型流形M上的連續小波變換關于函數與小波都保持了線性性質,平移性質和伸縮性質.流形M上函數f的連續小波變換可以看成是函數f與

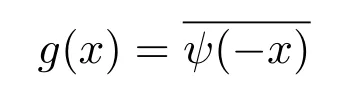
的卷積.所有這些結論對于我們后期進一步研究相應的離散情形提供了參考.同時,建立相應的應用算法將是一個值得考慮的研究問題.

[1]Daubechies I.Orthonomal basis of compactly supported wavelet[J].Comm.Pure and Appl.Math.,1998,41(7):909-996.

[2]Xu,Mingyao,etc.Introduction to fi nite group II[M].Peking:Science Press,2001.

[3]Lu Qikeng.Canonical manifold and classical domain[M].Shanghai:Shanghai Science and Technology Press,1963.

[4]Su Weiyi.Introduction to Modern Analysis[M].Peking:Peking university Press,2000.

[5]Rudin W.Fourier Analysis on Groups[M].Inter science,1967.

[6]Li Jinghui,Feng Xuning.Introduction to Topological Groups[M].Peking:Science Press,1999.

[7]Higgins P J.Introduction to Topological Groups[M].Cambridge:Cambridge University Press,1974.

[8]Montgomery D,Zippin L.Topolodical Transformation Groups[M].New York:Interscience Publishers,1995.

[9]Schaefer H H.Topological Vector Spaces[M].Berlin:Springer,1980.

[10]Helgason,S.Differential Geometry,Lie Groups and Symmetric Spaces[M]New York:Acad.Press,1978.

[11]Antoine P,Bogdanova I,Vandergheynst P.The continuous wavelet transform on conic sections[J].Int.J.Wavelets,Multiresolut.Inf.Process,2008,6:137-156.

[12]Antoine J P,Rosca D,Vandergheynst P.Wavelet transform on manifolds:Old and new approaches[J].Appl.Comput.Harmonic Anal.2010,28:189-202.

[13]Rosca D.On a norm equivalence on L2(S2)[J].Results Math.,2009,53:399-405.

[14]周小輝,王剛,王寶勤.廣義典型流形的實例構作[J].純粹數學與應用數學,2011,27(2):176-181.

[15]Wang Baoqin,Wang Gang,Zhou Xiaohui.A local wavelet transform on the torus T2[J].International Journal of Wavelets,Multiresolution and Information Processing,2015,13(4):1-5.

[15]Wang Baoqin,Wang Gang,Fu Yuexia,etal.The Mallat Algorithm for a class of orthogonal wavelet on compact Lie groups[C].Proceeding of 2009 ICWAPR,2009,2009:413-416.

[17]Wang Baoqin,Wang Gang,Yuan Lixia,etal.The wavelet transform and reconstruction formula on the generalized canonical manifold[C].proceedings of 2011 International Conference on wavelet analysis and Pattern Recognition(ISBN 978-1-4577-0280-8)(IEEE Catalog Number:CFD119C-PRT.

[18]Wang Baoqin,Wang Gang,Zhou Xiaohui,et al.Wavelet analysis on developable surface on area-preserving projection[J].Int.J.Wavelets Multiresolut Inf.Process.2015,13(1):1550007.

The properties of the continuous wavelet on the generalized canonical

Zhou Xiaohui1,2,Gu Guiding1,Wang Gang3

(1.School of mathematics,Shanghai University of Finance and Economics,Shanghai200433,China;2.Zhejiang University of Finance and Economics Dongfang College,Jiaxing 314408,China;3.School of mathematics science,Xinjiang Normal University,Urumqi 830054,China)

Some properties of the continuous wavelet on generalized canonical manifoldMwill be discussed in this paper.It is based on the structure of the generalized canonical manifoldMand the de fi nition of the continuous wavelet transform on generalized canonical manifold.It can be done that the linear property,translation property and dilation property of the continuous wavelet transform have been discussed on generalized canonical manifold.According to the properties of the generalized canonical manifoldM,the continuous wavelet onMcan be de fi ned,and some properties of the continuous wavelet on generalized canonical manifoldMsuch as the linear property,translation property and dilation property will be discussed in this paper.Finally the convolution formula of the continuous waveletψwill be given.

generalized canonical manifold,the continuous wavelet,general linear group GL(V)

2010 MSC:42C40,65T60

O189.3;O174

A

1008-5513(2017)06-0644-08

10.3969/j.issn.1008-5513.2017.06.010

2017-10-05.

國家自然科學基金(11371105,11671246);浙江財經大學東方學院教學科研課題(2017JK05).

周小輝(1986-),博士生,講師,研究方向：小波分析及其應用.