一類無圈型Nakayama代數的量

沈萍,陳正新

(福建師范大學數學與信息學院,福建 福州 350117)

一類無圈型Nakayama代數的量

沈萍,陳正新

(福建師范大學數學與信息學院,福建 福州 350117)

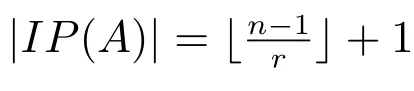
Nakayama代數;同調方法;代數的量

1 引言

在數學的許多領域,都存在關于給定對象大小的度量,如集合具有基數,向量空間具有維數,拓撲空間具有歐拉示性數等等.最近文獻[1]定義了具有廣泛存在性的富化范疇的量.富化范疇是滿足附加條件的單位半群范疇(或稱為張量范疇),要求其對象之間的Hom集不再是集合,而是原單位半群范疇中的對象.具有有限個對象的富化范疇的量是與其對象之間的Hom集相聯系的矩陣的逆矩陣中所有元素的和.在此框架下,拓撲空間的歐拉示性數、偏序集的M¨obius逆、度量空間的Minkowski維數等都與富化范疇的量密切相關,參見文獻[1-3].事實上,許多度量幾何和圖論中經典數量也與富化范疇的量密切相關,數學工作者們相信并期待富化范疇的量在更多數學分支中得到應用與發展,本文著重介紹富化范疇的量在域上有限維結合代數研究中的應用,其他的不做贅述.本文介紹域上具有有限總體維數的有限維代數的量的定義,并求出了一類特殊Nakayama代數的量.對域k上總體維數有限的有限維代數A,它的所有不可分解投射模構成了一個富化范疇,記為IP(A),稱富化范疇IP(A)的量為代數A的量.由于所有A-模都是投射A-模的同態像,而投射A-模總是所有不可分解A-模的直和的直和項,因此富化范疇IP(A)是A-模范疇中的重要構成部件.又由于所有不可分解投射A-模之間的Hom空間的維數恰好構成了代數A的Cartan矩陣,參見文獻[4],因此代數A的量(或富化范疇IP(A)的量)又可定義為代數A的Cartan矩陣的逆矩陣的所有元素求和,參見下面的定義.根據文獻[2]的主定理,我們也可以用同調方法計算代數的量.本文在文獻[2]的主定理的基礎上,計算一類Nakayama代數的單模之間同調群的維數,從而求出該Nakayama代數的量.

2 基本定義與記號

下面設k為代數封閉域,A為總體維數有限的有限維k-代數.本文中所有A-模均為左A-模,modA為全體有限維左A-模構成的模范疇.記{Si|i=1,2,···,n}為單A-模的全體,Pi(分別地,Ii),i=1,2,···,n,為Si對應的不可分解投射(分別地,內射)模.Pd Si(分別地,Id Si)表示單模Si的投射 (分別地,內射)維數.對正整數i,j,若i＜j,記 [i,j]表示集合{i,i+1,···,j?1,j}.記表示向下取整函數,如

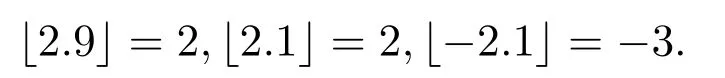
令

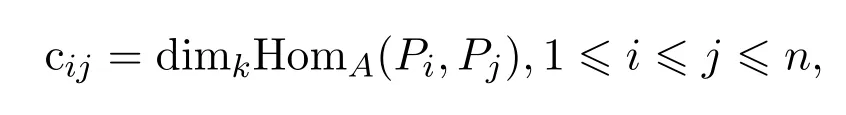
n階矩陣C=(cij)n×n,稱C為代數A的Cartan矩陣.

定義 2.1設A為總體維數有限的有限維k-代數,稱代數A的Cartan矩陣的逆矩陣的所有元素和為代數A的量,記為|IP(A)|.

定義 2.2[5]設M∈modA,若M的所有子模的集在包含關系下是線性有序的，即對M的任意兩個子模N和N′,或者N?N′,或者N?N′,則稱M是單列模.

定義 2.3[5]如果每一個不可分解投射右(左)A-模是單列模,則稱代數A是右(左)序列的.如果代數A既是左序列的又是右序列的,則稱代數A為Nakayama代數.

由文獻[5]定理3.2知,Nakayama代數可分為兩類,一類為底圖有圈的,另一類是底圖無圈的.本論文研究一類特殊的無圈型Nakayama代數A的量,A=kQ/I,其中箭圖Q為如下的線性箭圖:

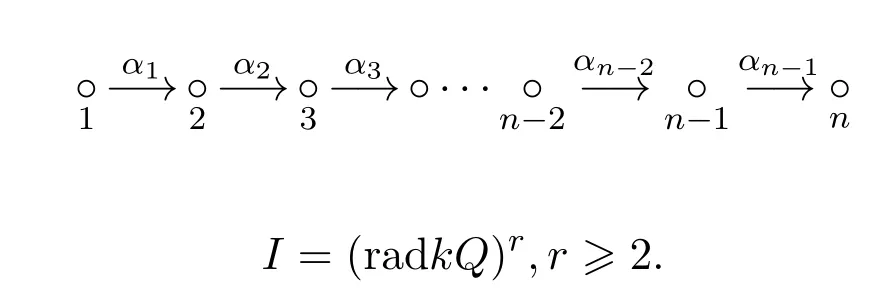
換句話說,I是kQ中由路長為r的所有路

所生成的理想.

本文以下部分中代數A總為上述Nakayama代數.對i≤j,由于Nakayama代數A中具有給定的socleSj及topSi的不可分解模是唯一的,可記該不可分解模為m(i,j),

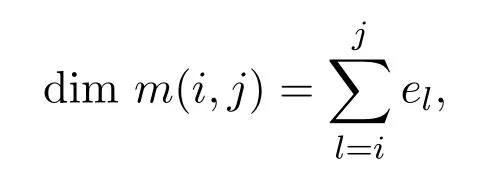
這里el表示第l個分量為1,其余分量為0的n維向量.

3 一些引理

由單列模的性質,對不可分解A-模N,其投射蓋Pi1一定為不可分解模.令f:Pi1→N為投射蓋,可得kerf為不可分解模,因此可得下面的引理3.1.

引理 3.1設M,N為不可分解模,若存在正合列

其中Pit,t=1,2,···,s,為不可分解投射模,則

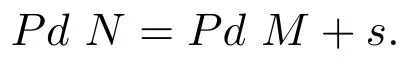
引理 3.2[6]設0→B→P→C→0為A-模中的正合列,其中P為投射A-模,則對任意的l≥1及A-模M,有

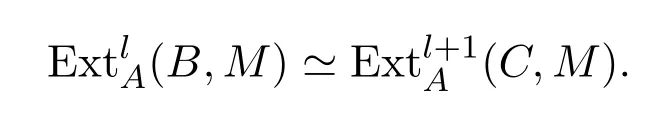
證明對正合列

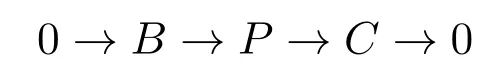
用函子Hom(?,M)作用,得到長正合列:

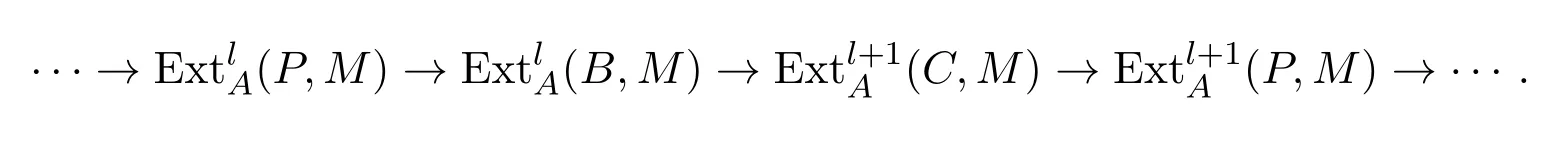
因為P為投射A-模,所以,從而有

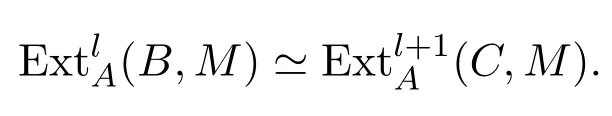
對偶地,可證如下引理:

引理 3.3設0→B→I→C→0為A-模中的正合列,其中I為內射A-模,則對任意的l≥1及A-模M,有

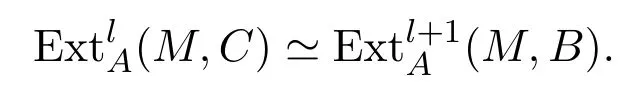
引理 3.4對任意的i=1,2,···,n,及非負整數t,若tr+i≤n,則

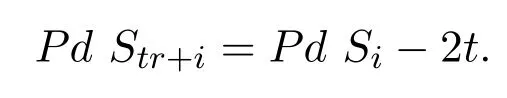
證明對t用數學歸納法.

當t=1時,有

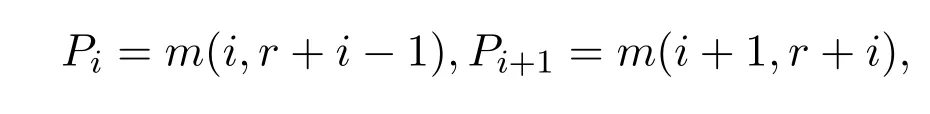
從而得到

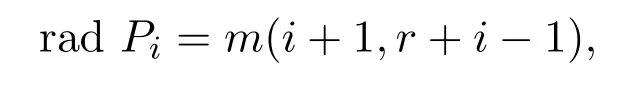
因此有下面的正合列:

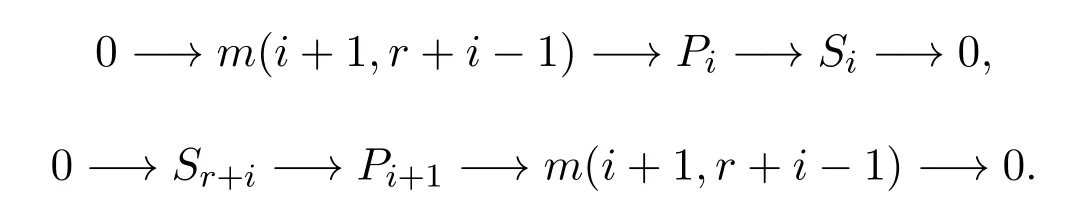
從而有正合列:

再由引理2.1得

假設等式

成立.下證等式

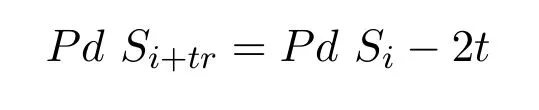
也成立.此時

并且

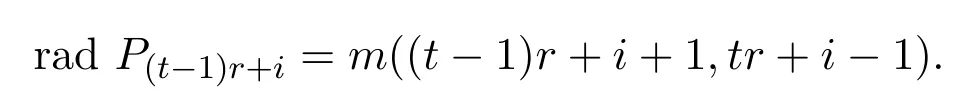
于是有下面兩個正合列:

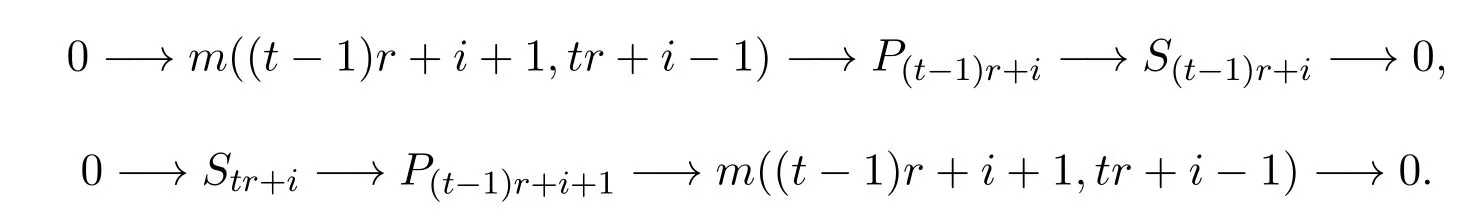
從而有正合列:

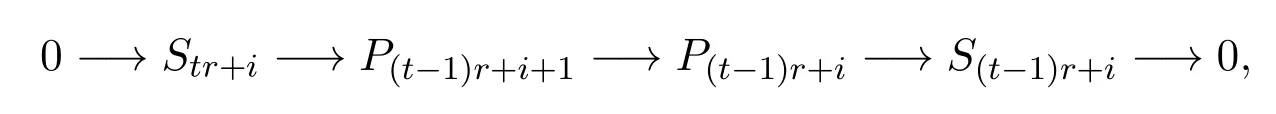
故有

又由歸納假設知

從而

對偶地,可證如下關于內射維數的引理:

引理 3.5對任意的i=1,2,···,n,及非負整數t,若tr+i≤n,則

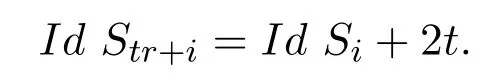
由Nakayama代數的性質及引理3.1,可證如下引理：

引理 3.6對任意的非負整數l,當i＞j時,有

證明設Pd Si=r.若l＞r,則

若l=0,

若1≤l≤r,令Si的投射分解式為:

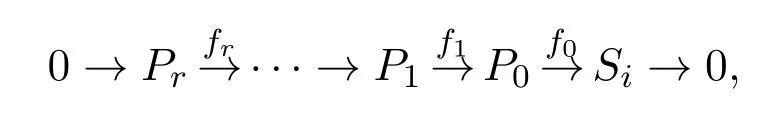
Ki=kerfi,0≤i≤r,則

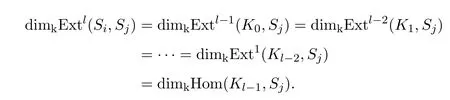
因為τi?j(Sj)=Si,則根據直向代數的性質

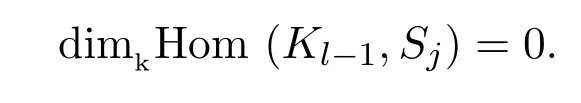
因此

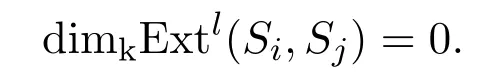
引理 3.7若j?i=tr,,則,且對任意l/=2t,

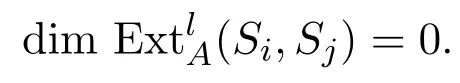
證明對t用數學歸納法.

當t=1時,有j?i=r,j=r+i,易知存在如下短正合列:

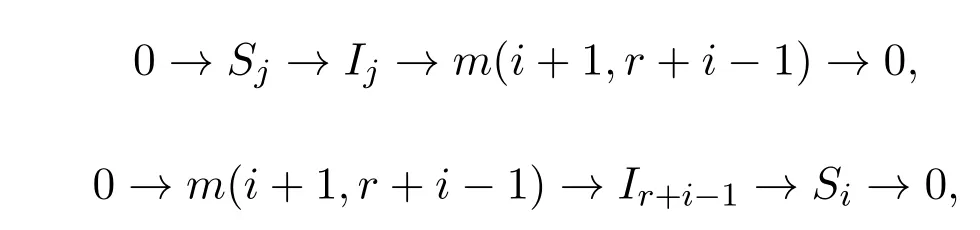
得到正合列:

故有

由引理3.6及上面的正合列知,對任意的l≥3,

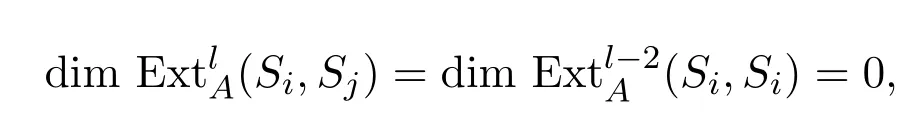
這就證明了此時引理成立.

假設當j?i=(t?1)r時,等式

且對l/=2t?2,

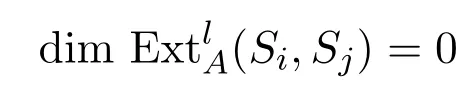
成立.下證:j?i=tr時,等式,且對l/=2t,也成立.易知存在如下短正合列:

于是有如下正合列:

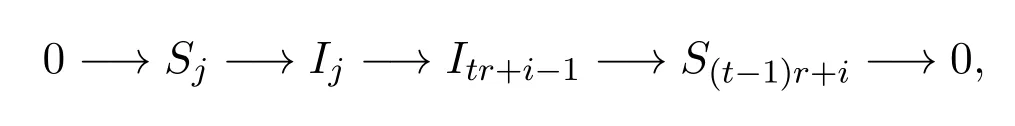
故有

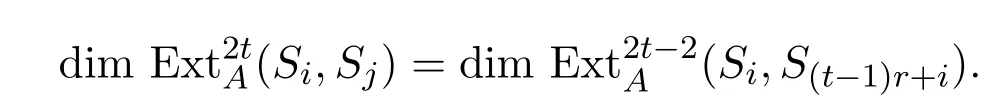
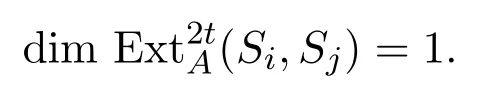
當l/=2t時,同理有

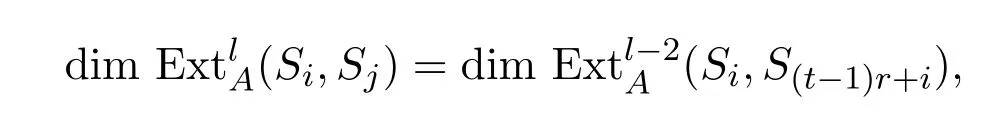
由歸納假設知,

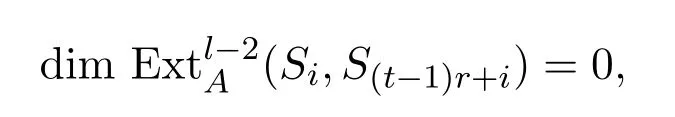
引理 3.8若j?i=tr+1,,則

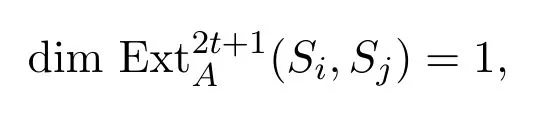
且對任意l/=2t+1,.

證明對t用數學歸納法.

若t=0時,則j=i+1.下面對j∈[2,n]分以下兩種情形證明引理成立.

情形 1j∈[r+1,n].此時，Ii=m(i?r+1,i),Ii+1=m(i?r+2,i+1),易知存在如下短正合列

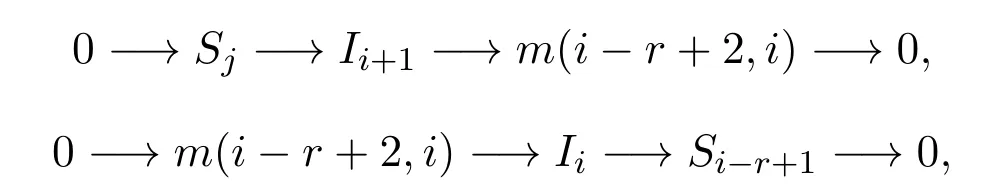
所以

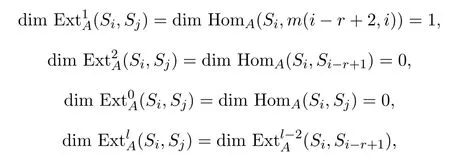
對任意的l≥3.因為r≥2,i?r+1＜i,從而由引理3.6知.故引理成立.

情形 2j∈[2,r].

此時Id Sj=1,從而,l≥2,易知存在如下短正合列:

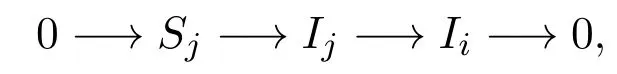
則

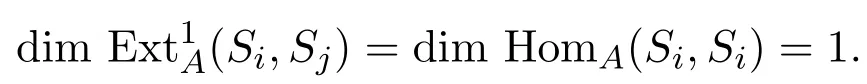
這就證明了此時引理成立.

假設j?i=tr+1時,等式,且對任意的l/=2t+1,

成立.下設j?i=(t+1)r+1.易知存在如下短正合列:

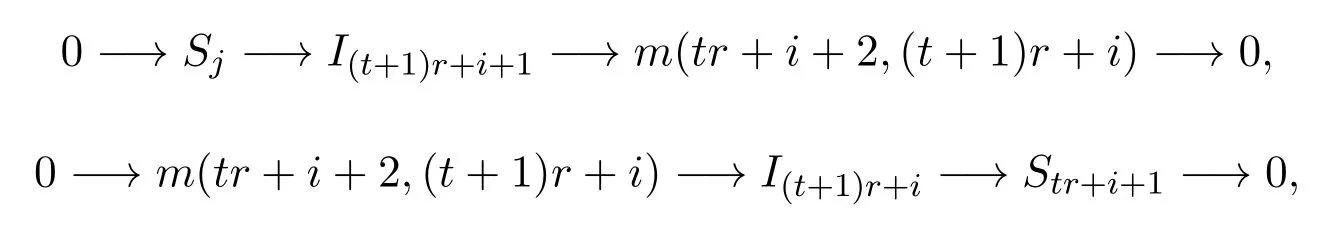
得到正合列:

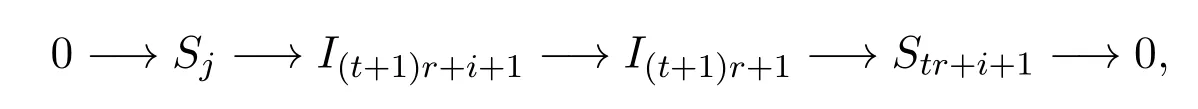
從而

由歸納假設知

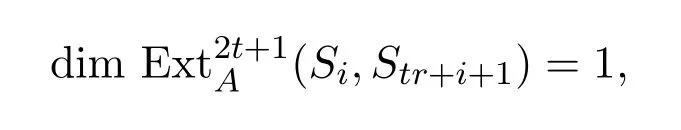
故

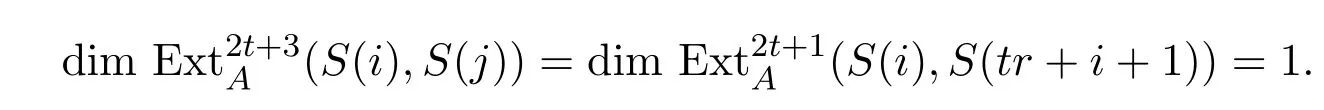
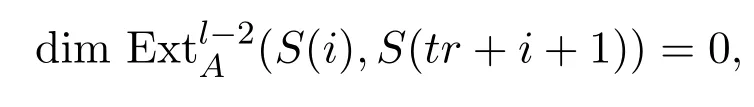
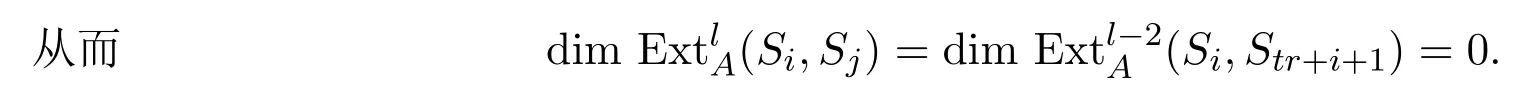
總之,由歸納可得引理對滿足條件的t均成立.

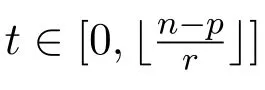
證明對t用數學歸納法.

若t=0,則j=i+p.對j∈[2,n]分以下兩種情形證明引理成立.

情形 1j∈[1,r].

此時Ip+i=m(1,p+i),Ip+i?1=m(1,p+i?1),易知存在如下短正合列:

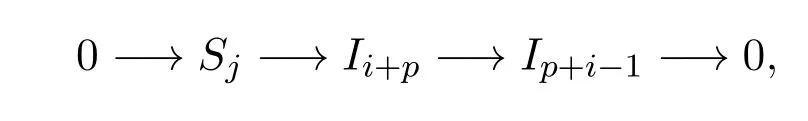
因此有

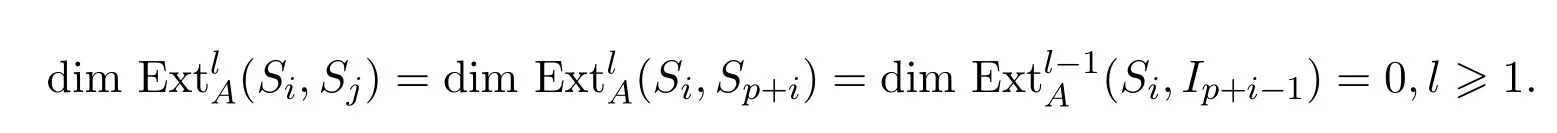
當l=0時,

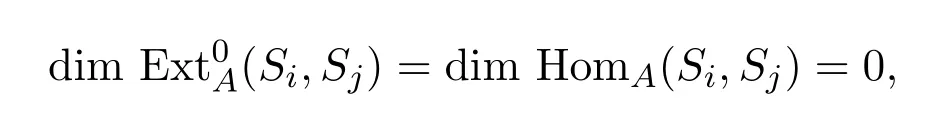
故此時引理成立.

情形 2j∈[r+1,n].

此時Ip+i=m(p+i?r+1,p+i),Ip+i?1=m(p+i?r+2,p+i?1),易知存在如下短正合列:

所以

對任意的l≥3.因為r≥2,p∈[2,r?1],i?r+p＜i,從而由引理3.6知.故此時引理成立

假設j?i=tr+p時,對任意的非負整數l,.下設j?i=(t+1)r+p.易知存在如下短正合列

得到如下正合列 0?→Sj?→Ij?→I(t+1)r+i+p?1?→Str+i+p?→0,所以

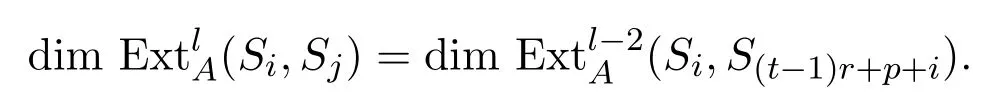
由歸納假設知

且對任意的l?2≥0,有,所以

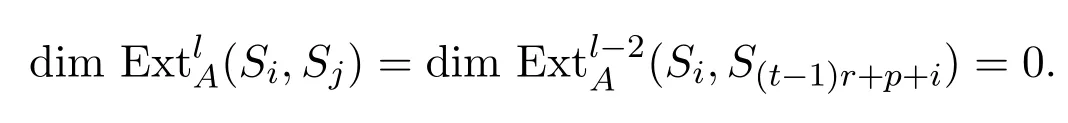
對l≥2,有

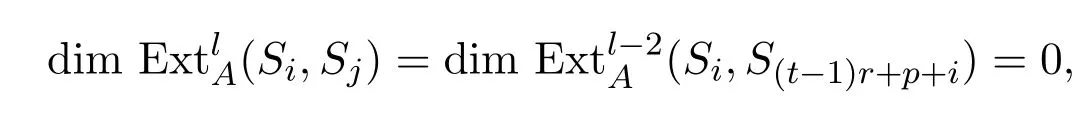
由前可知當l=0,1時,有.故引理成立.

總之,由歸納可得引理對滿足條件的t均成立.

4 定理的證明

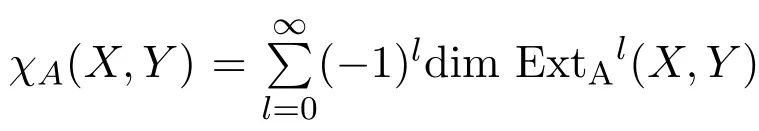
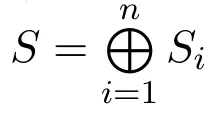
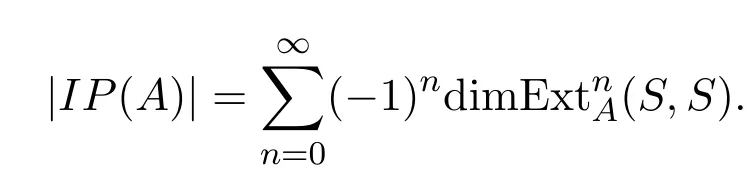
定理 4.2設k為代數封閉域,A=kQ/I為無圈型Nakayama代數,其中Q為含n個頂點的無圈箭圖,I=(kQ+)r,r≥2,令n=ar+x,則代數A的量

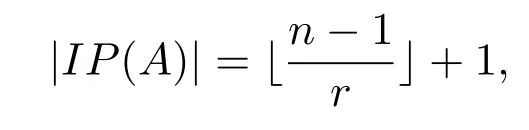
即當x=0時,|IP(A)|=a;當x/=0時,|IP(A)|=a+1.

證明對i,j∈[1,n],若i＞j,由引理3.6知,對任意的非負整數l,有,

則

若i＜j,可令j?i=tr+m,m∈[0,r?1].若j?i=tr時,由引理3.7知,

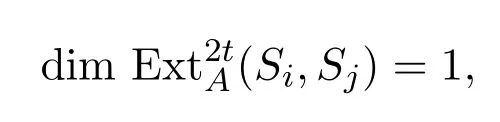
且對任意l/=2t,,則

若j?i=tr+1時,由引理 3.8知,,且對任意l/=2t+1,,則

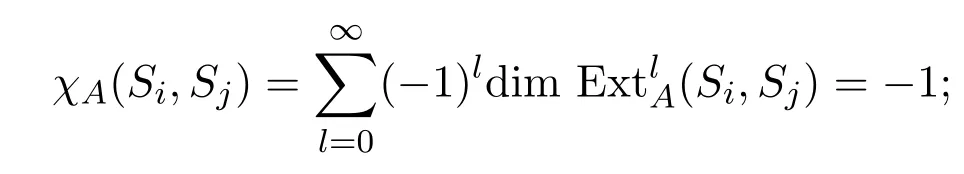
若j?i=tr+p,p∈[2,r?1]時,由引理3.9知,,則

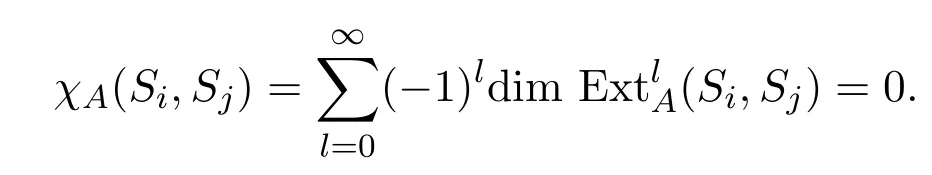
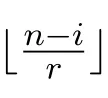
因此對給定的i∈[1,n?1],

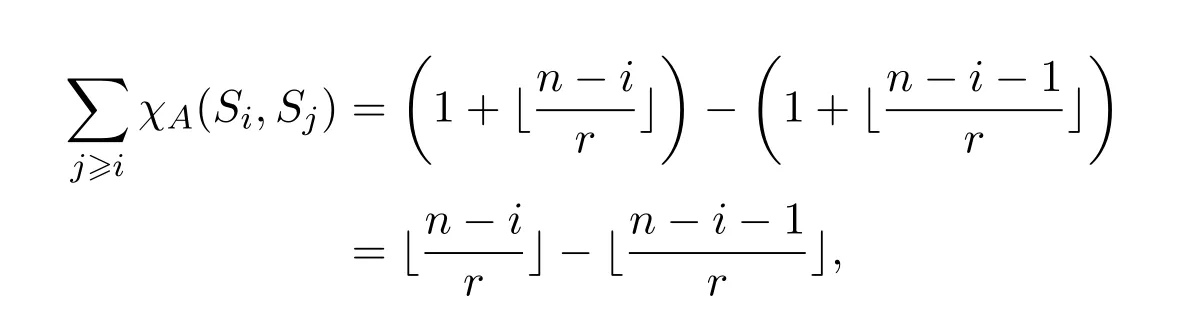
從而

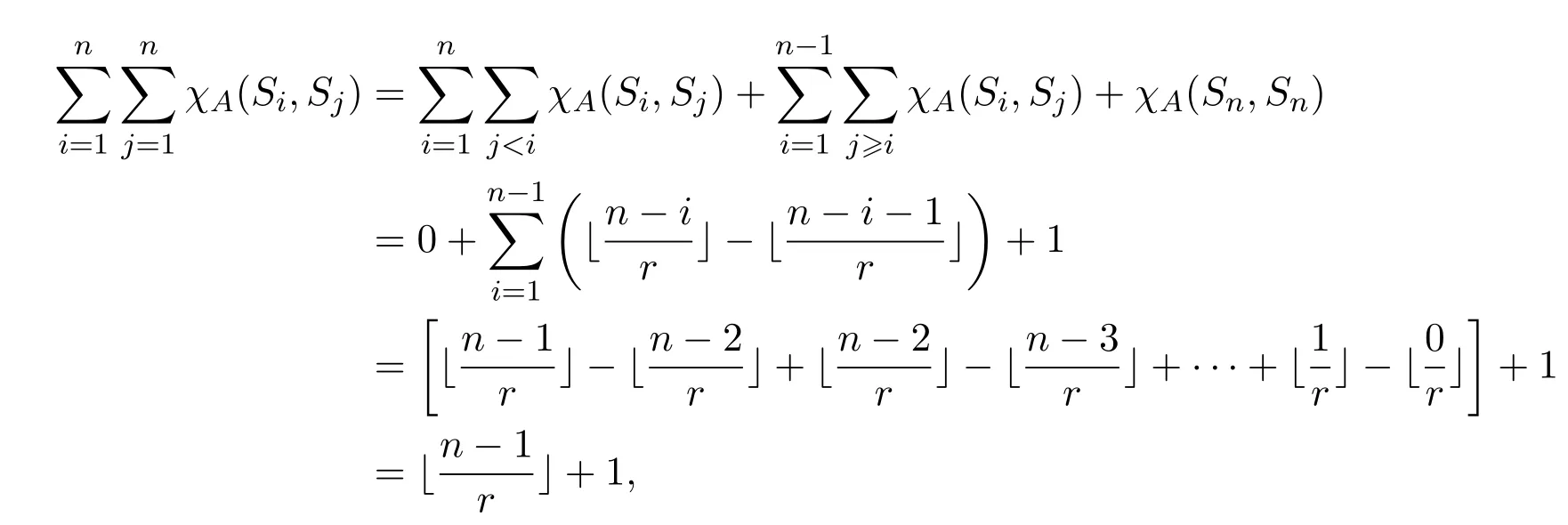
故由引理4.1,

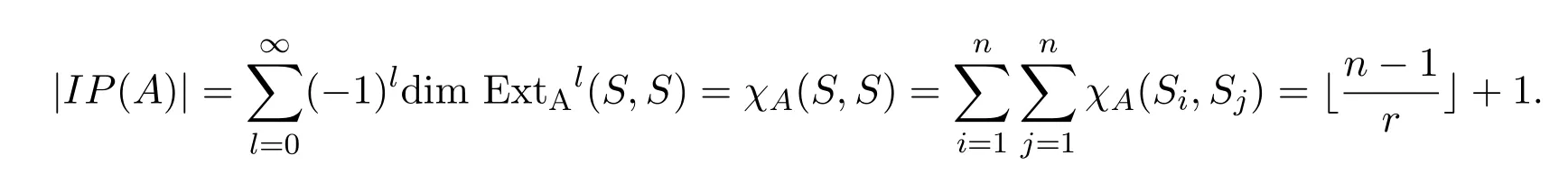
[1]Leinster T.The magnitude of metric spaces[J].Document Math.,2013,18:857-905.

[2]Chuang J,King A,Leinster T.On the magnitude of a fi nite dimensional algebra[J].Theory Appli.Categories,2016,31:63-72.

[3]Meckes M W.Magnitude,diversity,capacities,and dimensions of metric spaces[J].Potential Anal.,2015,42:549-572.

[4]Crawley-Boevey W.Lectures on representations of quivers[J].Commentarii Mathematici Helvetici,1992,69(1):137-141.

[5]Assem I,Simson D,Skowronski A.Elements of the Representation Theory of Associative Algebras[M].New York:Cambridge University Press,2006.

[6]佟文廷.同調代數引論[M].北京:高等教育出版社,1996.

Magnitudes of a class of Nakayama algebras with acyclic quivers

Shen Ping,Chen Zhengxin
(College of Mathematics and Informatics,Fujian Normal University,Fuzhou 350117,China)

Nakayama algebras,homomorphic method,magnitudes of algebras

2010 MSC:90C25

O178

A

1008-5513(2017)06-0623-11

10.3969/j.issn.1008-5513.2017.06.008

2017-09-01.

國家自然科學基金(11571360);福建省教育廳高校青年重點項目(JZ160427);福建省自然科學基金項目(2016J01006).

沈萍(1992-),碩士生,研究方向：代數表示論.