積分濾波非線性擬合科氏流量計驅動系統改進

徐同旭， 黃丹平,2,， 于少東， 郭康， 候山山

(1.四川理工學院機械工程學院， 四川自貢643000；2.人工智能四川省重點實驗室， 四川自貢643000；3.過程裝備與控制工程四川省高校重點實驗室， 四川自貢643000)

積分濾波非線性擬合科氏流量計驅動系統改進

徐同旭1， 黃丹平1,2,3， 于少東3， 郭康1， 候山山1

(1.四川理工學院機械工程學院， 四川自貢643000；2.人工智能四川省重點實驗室， 四川自貢643000；3.過程裝備與控制工程四川省高校重點實驗室， 四川自貢643000)

穩定振動的流量管保證著科氏流量計流量測量的準確性，而維持流量管振動的關鍵是流量計驅動系統。針對科氏流量計模擬驅動電路起振速度慢、受隨機干擾影響振動不穩定問題，研發基于積分濾波非線性擬合法改進驅動系統。改進驅動系統采用積分濾波方法削弱傳感器信號中隨機干擾，應用非線性擬合法對積分信號進行頻率估計，然后合成驅動信號驅動流量管振動。改進驅動系統中積分濾波可以有效抑制隨機干擾，非線性擬合法考慮信號整體不受個別采樣信號影響，提高頻率測量精度與增強振動穩定性。仿真實驗表明，基于積分濾波的非線性擬合法具有較高的頻率測量精度，適用于流量計起振頻率估計與振動頻率監測。實際改進驅動系統測試表明，改進驅動系統提高了流量計起振速度，增強振動穩定性。

科氏流量計;改進驅動系統;積分濾波;非線性擬合;合成信號驅動

引言

科氏質量流量計是發展迅速的新型質量流量計之一，因其測量流體質量具有高準確度、較長使用壽命與不受流體壓強、腐蝕性影響的特點，在工業上得到廣泛應用。科氏流量計[1]主要由兩部分組成，其一為一次儀表(又稱流量傳感器)，由流量管、速度傳感器、溫度檢測傳感器、電磁激振器組成；其二為二次儀表(又稱流量變送器)，由信號處理系統、顯示模塊和驅動系統組成，其中驅動系統為流量管穩定振動提供能量，是流量計正常、準確工作的前提。

國外對科氏流量計驅動系統研究，主要以專利形式出現，國內以徐科軍為代表，在科氏流量計驅動方法上作了一些研究，如科氏流量計模擬驅動方法研究[1]、基于FPGA的科氏流量計驅動技術實現[2]等。國內廠商基本使用模擬驅動系統驅動流量管振動，模擬驅動系統是自激振動系統，易受干擾信號影響，導致流量管起振時間慢與振動不穩定，從而影響流量測量的準確性。

波形合成驅動方法可以快速提高流量管起振時間與增強振動穩定性，可有效避免隨機干擾影響，其信號頻率估計至關重要。因此，為提高流量管起振速度與增強振動穩定性，提出在積分濾波基礎上，采用非線性擬合方法估計信號頻率，然后合成驅動信號驅動流量管振動。

1 模擬驅動系統及改進方法

在模擬驅動系統基礎上改進驅動系統的流程如圖1所示。模擬驅動系統由一次儀表、初級放大電路、低通濾波、自動增益控制模塊、功率放大模塊組成，該系統為自激振動[3-8]系統。模擬驅動系統自動增益控制模塊實時跟隨傳感器信號，易跟隨信號中干擾，導致驅動信號不穩定。因而在改進驅動系統中，采用積分濾波與非線性擬合頻率估計算法，合成驅動信號驅動流量管振動。

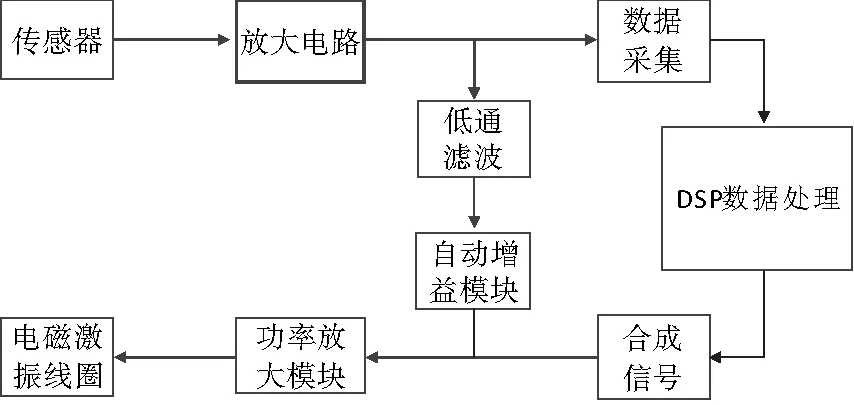
圖1科氏流量計改進驅動系統

合成驅動信號流程如圖2所示。在模擬驅動工作時，采集傳感器數據，對其進行積分濾波與頻率預估計，然后對積分濾波后數據進行非線性擬合，估計出頻率值，并與上次頻率值進行對比，判斷是否滿足頻率精度要求。若滿足則合成驅動信號，通過功放直接驅動流量管；若不滿足，則繼續下一輪頻率估計。改進部分不僅在起振初期工作，在流量測量過程中一直運行。若頻率發生變化則可自動調整驅動信號頻率，實現對流量管主頻跟蹤及驅動流量管穩定振動。

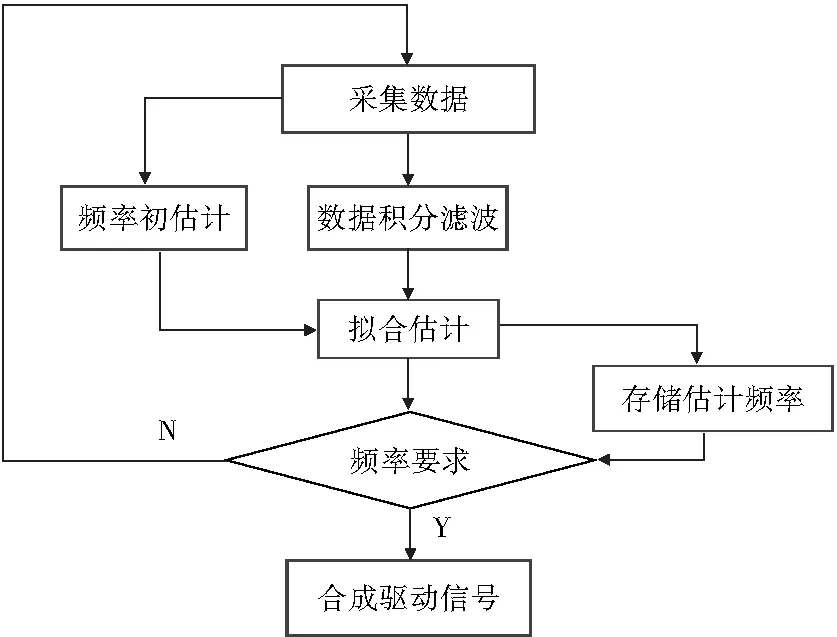
圖2合成驅動信號流程

2 基于積分濾波非線性擬合法

2.1 信號頻率對起振的影響

不同頻率合成信號驅動流量管時，其傳感器信號幅值包絡及起振時間有所區別。模擬驅動傳感器輸出信號可參考文獻[9]里面的數據波形，現對中測科技有限公司的TH010型流量計進行測試，使用幾個頻率值驅動信號驅動流量管，實驗結果如圖3所示。由圖3可知，在一定頻率范圍內不同頻率信號驅動，傳感器信號峰值不同，且穩定快慢有所差別，只有接近主頻信號驅動更快。

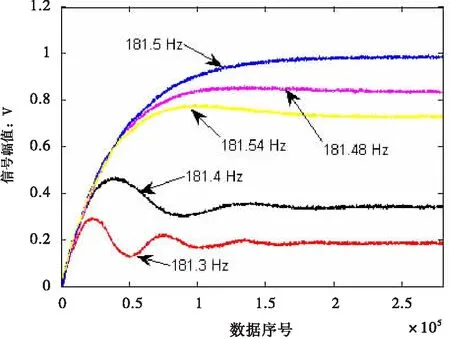
圖3傳感器信號幅值包絡曲線

實際模擬驅動系統，傳感器信號濾波后仍會帶有隨機干擾，這些干擾將影響頻率估計精度，進而影響合成信號驅動效果。積分濾波可以有效削弱信號中隨機干擾成分，故采用積分濾波法對信號進行濾波處理。

2.2 積分濾波

流量管的快速起振、穩幅與信號頻率密切相關。在合成信號時，頻率估計的準確度至關重要。采集信號中隨機干擾信號，其信號幅值在0 mV～35 mV之間，大幅值干擾信號將影響流量計頻率估計精度。

對于采集信號，相鄰離散數據所受干擾同正負概率不大，連續幾個采集數據所受干擾同正負的概率更小。利用連續采集數據所受干擾同正負的小概率事件，對其進行積分(求和)，隨機噪聲相互削弱，從而在積分信號中減少噪聲影響。

對于幅值為A、頻率ω、初相φ的流量計信號x(t)=Asin(ωt+φ)，其在區間[t,t+L]內的積分為：

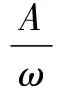
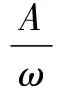
C0?bsin(ωt+α)+C

(1)

在離散采樣信號x(n)=Asin(ωnΔt+φ)中，算法實現步驟如下：

第一步，離散采集N(N>100)個數據，設置積分數據長度為10。

第二步，積分后數據y(k)，1≤k≤N-9，其中積分值為：

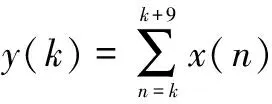
(2)

疊加隨機干擾的正弦信號與進行積分濾波后的仿真結果如圖4所示。從仿真實驗可知，積分濾波有效削弱了隨機干擾對信號的影響。結合公式(1)，積分后的信號為與原信號同頻率正弦信號，且信號整體產生固定偏移。故可用積分后信號進行頻率估計，且因隨機干擾的削弱，有利于提高頻率測量精度。

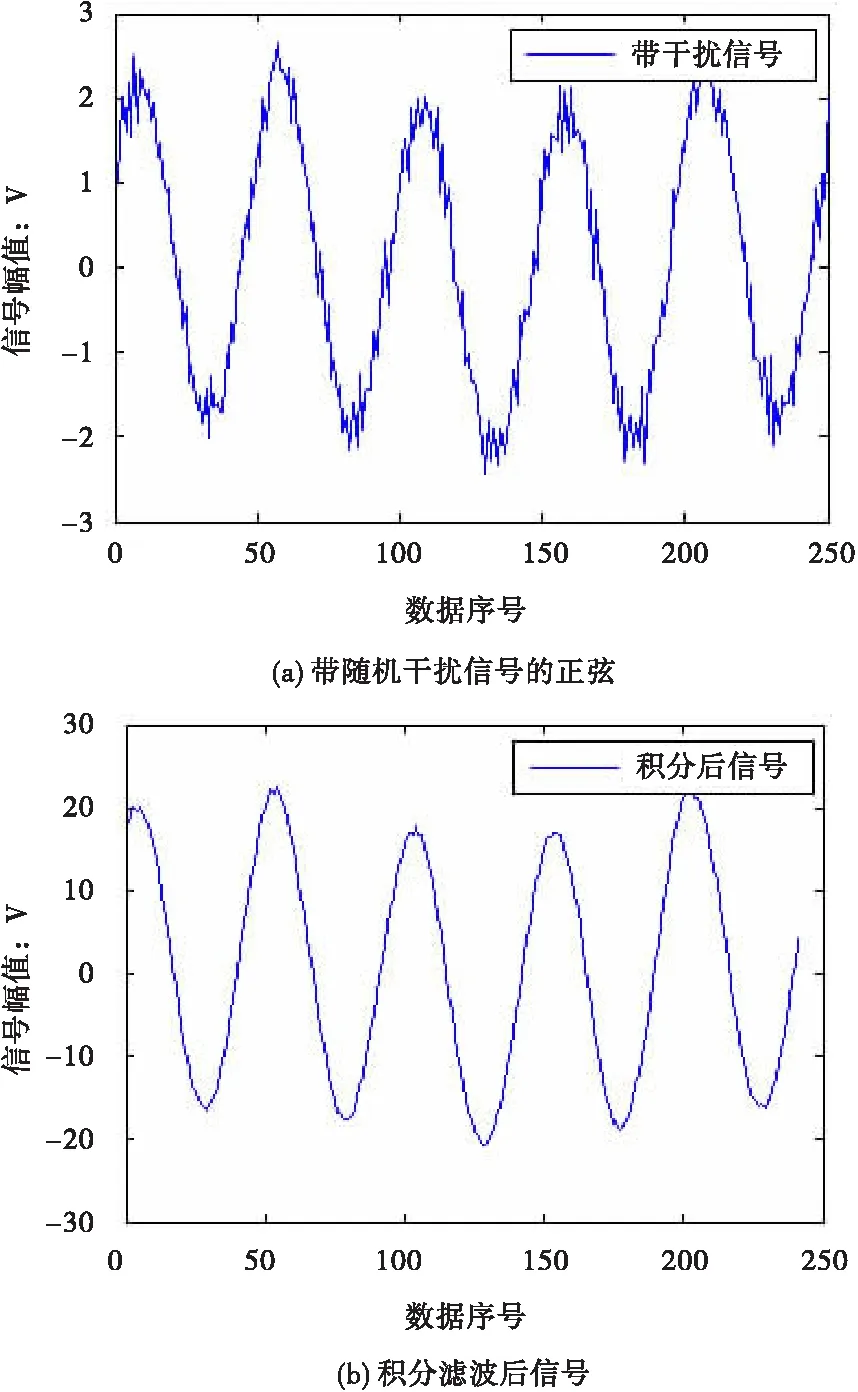
圖4積分濾波仿真實驗結果

2.3 非線性擬合法

頻率估計[9-15]經典方法過零檢測法，算法簡單快速，但其在估計信號頻率時，要求信號采集數據長度大于1倍周期，且對數據零點穩定性要求高。然而隨機干擾對零點信號有影響，從而影響過零檢測法頻率測量精度。因非線性擬合法考慮信號整體，不受信號零點值的影響，故而采用非線性擬合方法來測量信號頻率。

非線性擬合法[16-17]是數據關系預測算法，常用來分析數據之間的關系。常用的擬合函數為二次多項式、三次多項式、切比雪夫多項式和高階多項式，通常使用時未知數據變量之間的關系。在科氏流量計信號處理中，由于傳感器輸出信號為帶干擾正弦信號，其理論波形已知，故可以直接使用正弦函數對積分后信號進行擬合。設擬合函數為：

z(t)=Bsin(ωt+γ)+d

(3)

擬合函數的求解，即是求出使最小二乘函數G(B,ω,γ,d)值最小的參數B、ω、γ和d，其中最小二乘函數為：

(4)

對于公式(4)中最小二乘函數最小值求解，若直接搜索四維參數空間，數據計算量龐大。對積分信號去偏置，則公式(4)將變為：

(5)

顯然，此函數值與幅值B是線性相關，擬合信號相當于非偏置信號壓縮映射，不影響信號頻率、相位。故可以簡化最小二乘函數，可得優化函數：

(6)

其中B0為去偏置積分信號最大值。此時，頻率、相位參數求解變為二維參數空間搜索參數值，數據計算量相對于四維參數空間極大降低。

頻率、相位參數空間下優化函數取值曲面如圖5所示。由圖5(a)可知，優化函數有唯一最小值，多個極大值。結合圖5(b)優化函數等值線圖，可知當相位在一定范圍取定值、頻率在一定取值區間時，優化函數值是頻率的凹函數，可取到最小值。同樣，當頻率在一定范圍取定值、相位在一定區間取值時，優化函數值也是相位的凹函數，可取到最小值。

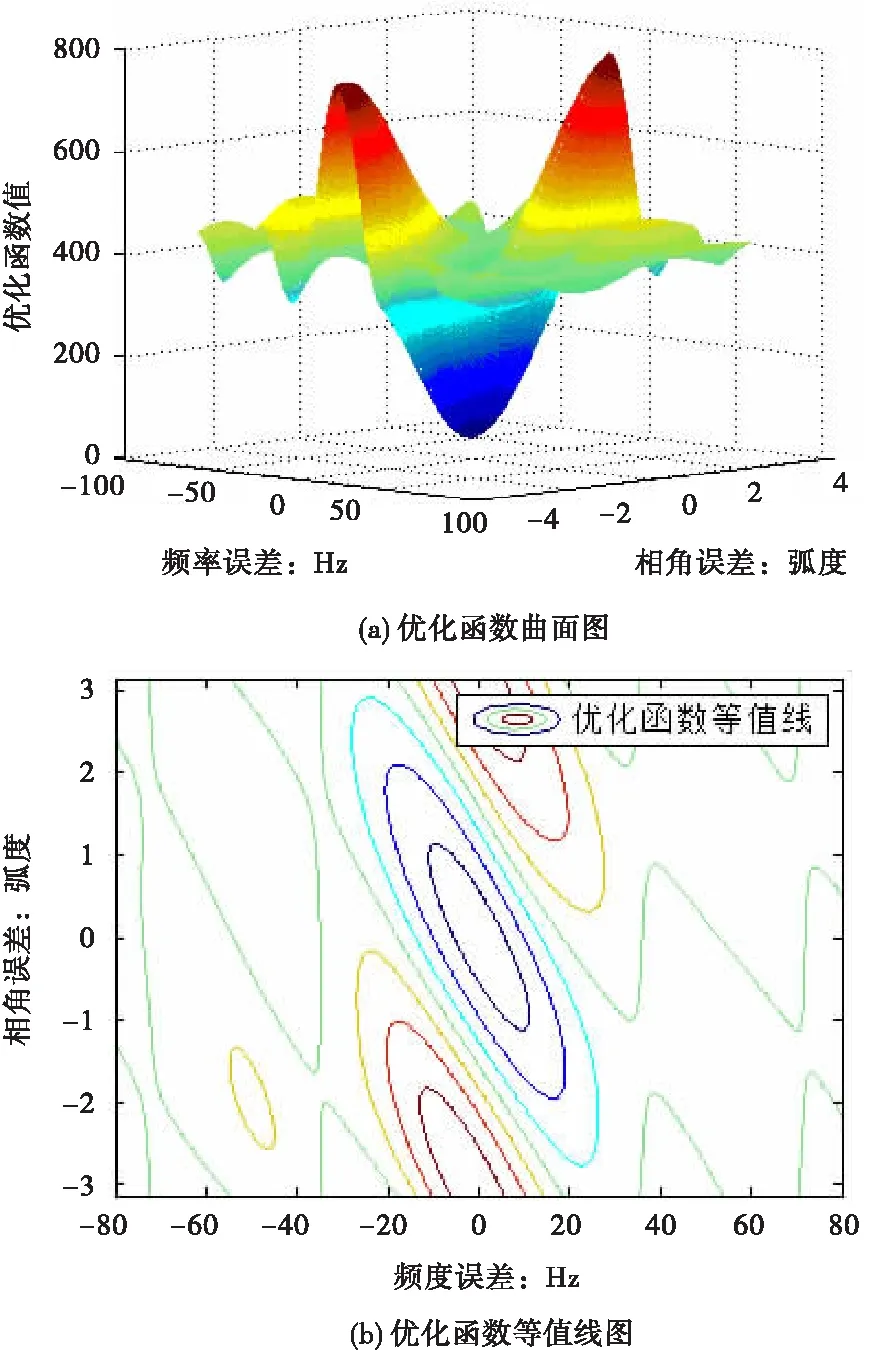
圖5參數空間下優化函數值

因此，參數搜索采用二分法，分別對頻率、相位進行搜索，求出滿足頻率、相位精度要求的參數。積分后流量計信號非線性擬合法步驟如下：

Step 1對積分后信號去偏置，設偏置參數d0，去偏置信號y*(n)=y(n)-d0，其中

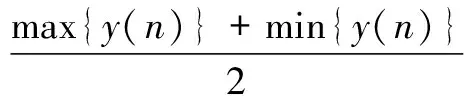
Step 2過零檢測法估計頻率初始值f0，估計出相位初始值γ0，ω0=2πf0，參考優化函數等值線，給出頻率參數區間[f0-15,f0+15]、相位參數區間[γ0-1.5,γ0+1.5]。

Step 3設置頻率搜索精度ef=0.001 Hz，相位搜索精度eγ=0.001 弧度。

Step 4取相位區間邊值γ1、γ2，對給定頻率搜索區間，采用二分法，計算優化函數S(ω,γ)數值，得到滿足頻率精度的函數值S1、S2，以及頻率f1、f2。

Step 5若γ1-γ2≤eγ，則轉Step 7，否則轉Step 6。

Step 6改變相位值γ1、γ2， 其中

轉Step 4。

Step 7搜索結束，優化函數參數為γ=γ1，ω=2πf1，優化函數值為S1。

在上述第3步中所給參數精度，滿足流量計合成信號驅動對頻率精度要求，可在100步以內得出滿足精度要求的結果。

3 仿真實驗

為進行對比，采用過零檢測法與本文算法進行仿真對比。表1為在信號頻率為181 Hz、采樣頻率為9000 Hz、固定頻率比(約49.723)，在不同信噪比水平下仿真實驗。表2為同一信噪比水平，不同頻率比下仿真實驗。

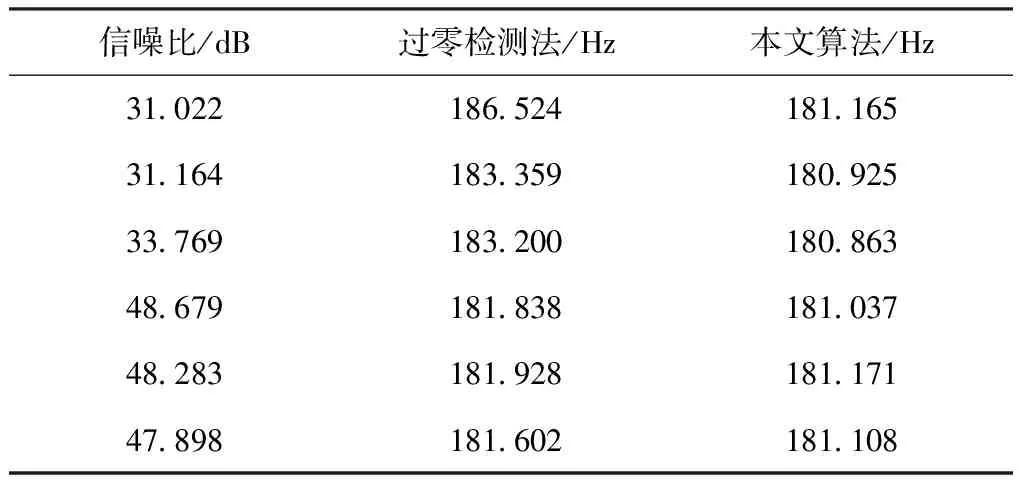
表1不同信噪比算法頻率估計仿真結果

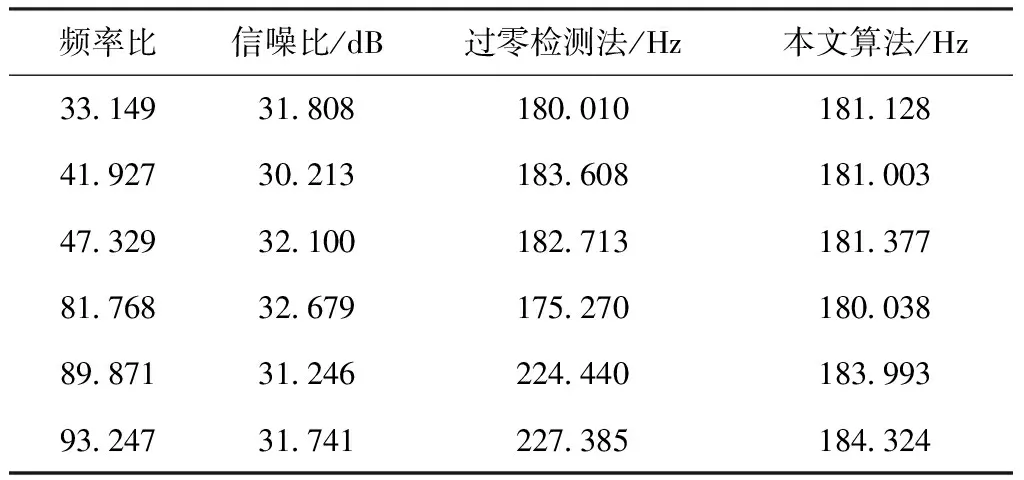
表2不同頻率比下算法頻率估計仿真結果

由表1中數據可知，在信噪比較小時，測量精度較低，但本文算法在幾組實驗中具有較高精度。表2中數據可知，在不同頻率比值下，本文算法頻率估計結果優于過零檢測法，在后面三組數據中，過零檢測法頻率估計結果誤差大。

為了確定不同頻率比與信噪比下采樣信號對算法估計值影響，在181 Hz信號頻率下，通過改變采樣頻率(即改變頻率比值)，及在不同信噪比水平上進行100組仿真測試，結果如圖6所示。

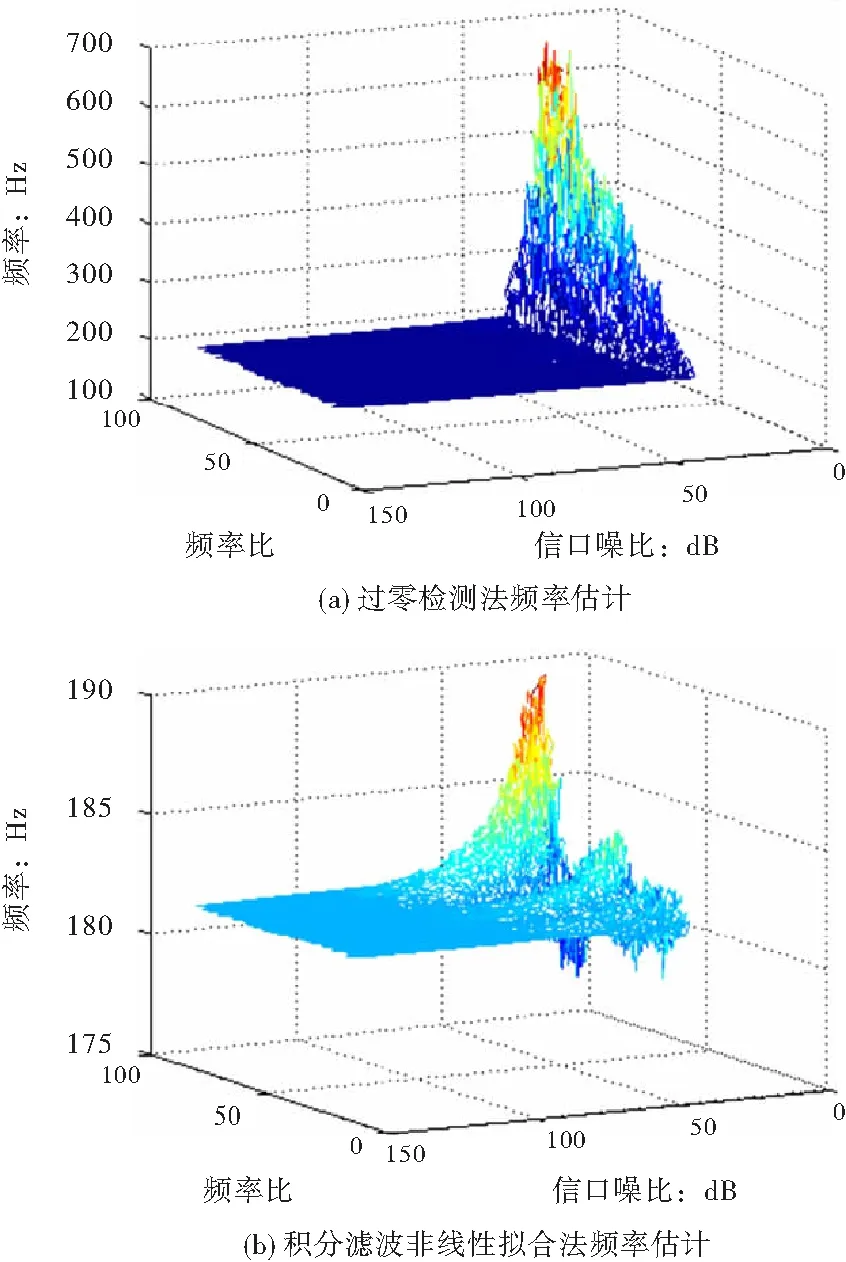
圖6參數變化下算法頻率估計仿真結果

對比圖6(a)與圖6(b)可知，在信噪比降低時，算法頻率估計誤差增大，且在低信噪比下，隨著頻率比的增加，頻率估計誤差具有變大趨勢。盡管如此，基于積分濾波擬合算法在低信噪比下具有相對較高的頻率估計精度。取仿真實驗中三個信噪比水平，在不同頻率比下算法估計的相對誤差實驗數據，結果如圖7所示。

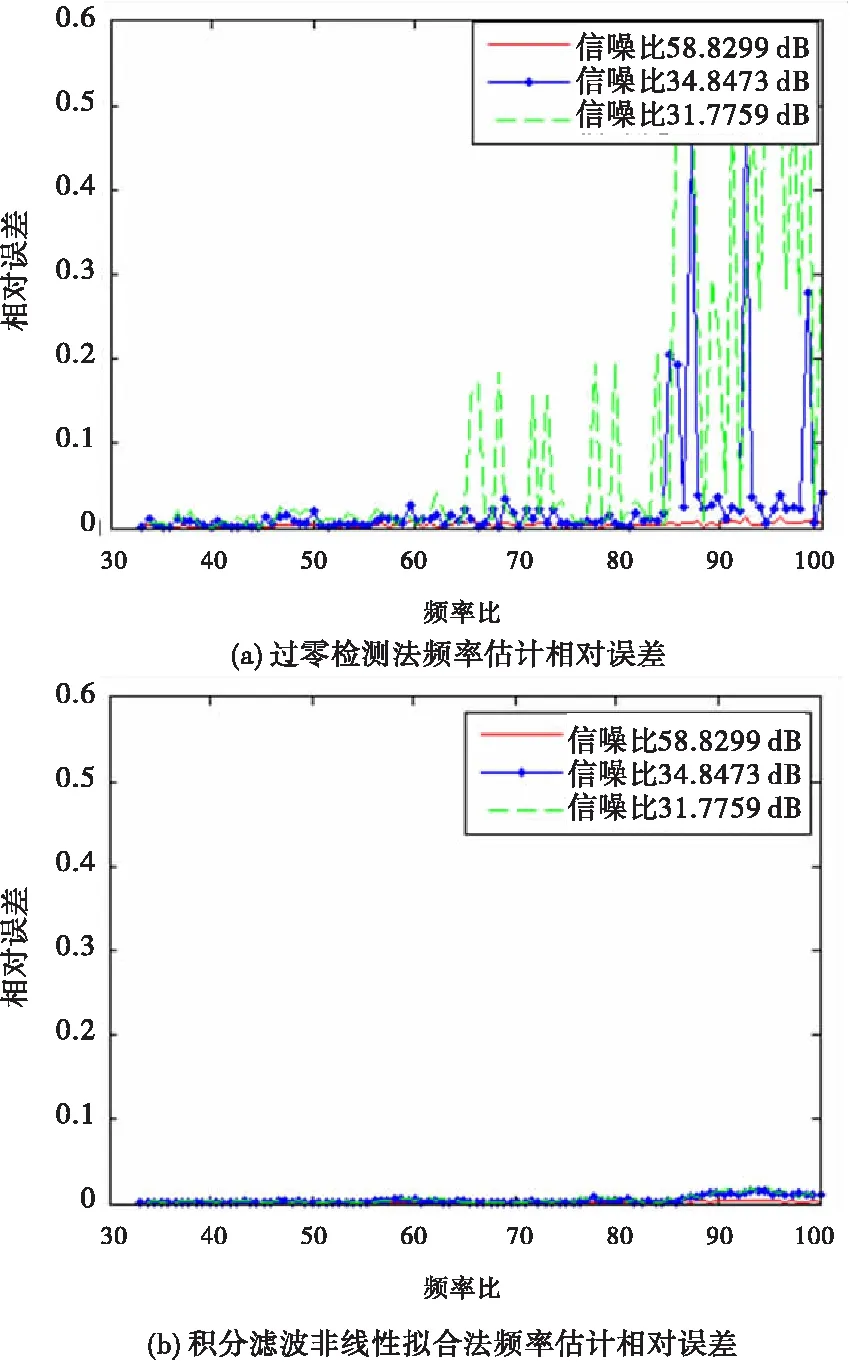
圖7算法頻率估計相對誤差比較

由圖7可知，不同頻率比下，基于積分濾波擬合算法頻率估計值的相對誤差小于過零檢測法。此外，可看出在三組信噪比下，頻率比對基于積分濾波擬合算法頻率估計影響變化趨勢，為驅動系統中采集數據時采樣頻率設置提供了依據。

通過以上仿真測試，基于積分濾波非線性擬合法能有效提高頻率估計精度，利于流量計起振速度提高，以及穩定振動時對頻率變化的監測。

4 改進驅動系統起振測試

四川中測科技發展有限公司TH010型流量傳感器作為測試對象，流量計傳感器流量管主頻約為181 Hz，流量計準確度0.5級，使用所研發改進驅動系統進行起振測試。測試中，采用NI的PCI-1747U數據采集卡采集傳感器輸出信號。

采集結束，導出驅動系統內部頻率估計數據到PC機，同時將采集數據導入到Matlab中，以便于觀察傳感器信號起振時間曲線。圖8(a)為改進驅動系統流量管起振傳感器信號曲線圖，圖8(b)為頻率估計曲線。在流量計上電后約0.46 秒內，頻率估計值遠大于181 Hz，在約0.7 秒時傳感器呈現出正弦波形，此后合成信號驅動流量管。圖8(b)只顯示了合成信號驅動以后對傳感器信號進行頻率估計的結果。

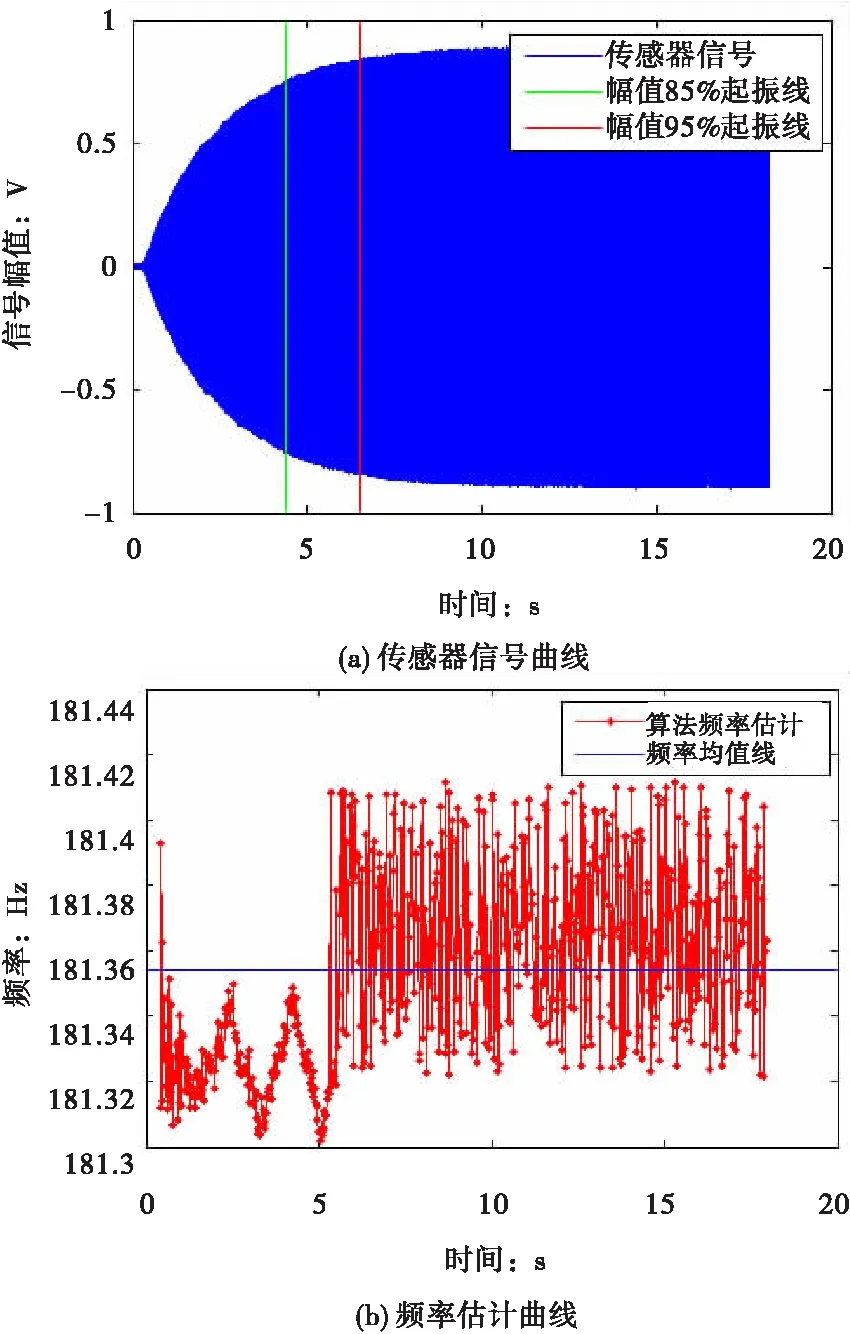
圖8起振曲線與頻率估計曲線

文獻[12]中模擬驅動以達到穩定幅值80%的時間作為流量管起振時間，其起振時間約為22秒。在模擬驅動系統下，TH010型流量計傳感器信號幅值達到穩定幅值80% 時間約13 秒，從圖8(a)可知，改進驅動系統在穩定幅值85%、95%時起振時間均優于傳統模擬驅動。

5 結束語

針對科氏流量計模擬驅動起振速度慢，受干擾信號影響導致振動不穩定問題，提出了基于積分濾波非線性擬合法估計信號頻率，合成驅動信號驅動流量管振動的改進驅動系統。合成信號驅動方法避免了模擬驅動因干擾信號導致驅動不穩定問題，驅動流量管振動更穩定。積分濾波非線性擬合法能有效抑制隨機干擾，提高頻率測量精度。實際起振測試結果表明，基于積分濾波非線性擬合法科氏流量計改進驅動系統有效提高了起振速度與振動穩定性。

[1] 徐科軍,徐文福.科氏質量流量計模擬驅動方法研究[J].計量學報,2005,26(2):149-154.

[2] 李志勇,張英敏,張鵬.基于FPGA的科氏流量計驅動技術實現[J].測控技術,2010,29(2):4-7.

[3] 徐科軍,于翠欣,蘇建徽,等.科里奧利質量流量計激振電路的研制[J].合肥工業大學學報:自然科學版,2000,23(1):37-40.

[4] HENRY M P,ZAMORA M E.Start up and operational techniques for a digital flowmeter:US,6950760[P].2005-09-27.

[5] 黃丹平,汪俊其,于少東,等.科氏質量流量計新型模擬驅動電路研究[J].自動化與儀表,2016,31(1):71-76.

[6] 李苗,徐科軍,朱永強,等.科氏質量流量計的3種驅動方法研究[J].計量學報,2011,32(1):37-39.

[7] 陶波波,徐科軍,侯其立,等.變傳感器設定值的科氏質量流量管控制方法[J].儀器儀表學報,2015,36(3):712-719.

[8] 黃世震,歐陽鋒.科氏質量流量計驅動系統模糊PI控制方法[J].太赫茲科學與電子信息學報,2014,12(1):127-131.

[9] 汪正軍,潘磊,紀國瑞.基于離散相位差檢測的頻率測量方法[J].儀器儀表學報,2013,34(5):994-999.

[10] 涂亞慶,蘇奮華,沈廷鰲,等.自適應陷波器的科氏流量計信號頻率跟蹤方法[J].重慶大學學報:自然科學版,2011,34(10):147-152.

[11] CHEN K,ZHENG D,FAN S,et al.Novel Coriolis mass flowmeter signal processing algorithms based on DFT and digital correlation[C]//Proceeding of 2010 IEEE Symposium on industrial electronics & applications,Penang,Malaysia,October 3-5,2010:56-60.

[12] 金艷,王利軍,胡亮,等.科氏流量計測量管固有頻率在線預測方法[J].計量學報,2017,38(3):328-332.

[13] 林偉,趙靜蕾.一種基于希爾伯特變換的科氏流量計信號處理算法[J].電子器件,2016,39(5):805-808.

[14] 任建新,暴苗剛,張鵬,等.一種基于自適應陷波器的科氏流量計頻率解算新方法[J].傳感技術學報,2012,25(4):339-343.

[15] 任建新,邊琦,張鵬,等.一種基于SVD和改進自適應算法的科氏流量計氣體信號頻率解算方法[J].傳感技術學報,2013,26(10):1405-1408.

[16] 楊輝躍,涂亞慶,張海濤,等.科氏流量計振動信號參數估計的最小二乘法[J].計算機工程與應用,2016,52(3):252-255.

[17] 胡運權,郭耀煌.運籌學[M].3版.北京:清華大學出版社,2007.

Improvement of the Driving System of Coriolis Mass Flowmeter Based on Integral Filter and Nonlinear Fitting

XUTongxu1,HUANGDanping1,2,3,YUShaodong1,GUOKang1,HOUShanshan1

(1.School of Mechanical Engineering, Sichuan University of Science & Engineering, Zigong 643000, China; 2.Artificial Intelligence Key Laboratory of Sichuan Province, Zigong 643000, China; 3.Sichuan Provincial Key Lab of Process Equipment and Control, Zigong 643000, China)

The drive circuit is the key factor whether the Coriolis mass flow meter can work normally. The flow pipe sometimes vibrates unsteadily due to random noise in the analog driving system and its completed oscillation cause much time. In order to decrease the start-oscillation time and increase vibration stability, an improved driving system, which based on integral filter and nonlinear fitting algorithm, has been put forward. In this improved driving system, the integral filter is used by calculating a summation of acquisition data, which has a better effect in decreasing noise. Then nonlinear fitting has been used to estimate the frequency of acquisition signal. The nonlinear fitting operating on the whole signal, as for its estimation will not be affected by the extra noise. The simulation results show that the improved algorithm has high accuracy than traditional algorithm. And experiments indicate that the improved driving system has a short time when the flow pipe vibrating stability, and improves the oscillation stability.

coriolis mass flow meter; improved driving circuit; integral filter; nonlinear fitting; composite signal

1673-1549(2017)06-0023-07

10.11863/j.suse.2017.06.05

2017-09-14

過程裝備與控制工程四川省高校重點實驗室開放基金項目(GK201602)

徐同旭(1991-)，男，江蘇淮安人，碩士生，主要從事智能儀器儀表方面的研究，(E-mail) 1966500807@qq.com

黃丹平(1968-),男，四川自貢人，副教授,博士,主要從事測控技術方面的研究,(E-mail)18739185581@163.com

TH814.6

A