空間幾何和解析幾何核心考點B卷答案
空間幾何和解析幾何核心考點B卷答案
一、選擇題
1.D 2.C 3.A 4.A 5.D 6.D 7.B
8.A 9.B 1 0.D 1 1.C 1 2.B 1 3.B
1 4.B 1 5.D 1 6.D 1 7.B 1 8.D 1 9.D
2 0.B 2 1.A 2 2.C 2 3.D 2 4.C 2 5.C
2 6.A 2 7.C 2 8.A
二、填空題
三、解答題
4 2.(1)x2+y2表示圓上的點P(x,y)到原點的距離的平方。因圓心到點P(x,y)的距離為2,所以|P O|的最大值為3,從而x2+y2的最大值為9。
4 3.(1)因為底面A B C D是菱形,∠A B C=6 0°,所以A B=A C=A D=a。在△S A B中,由S A2+A B2=2a2=S B2,知S A⊥A B。同理S A⊥A D。所以S A⊥平面A B C D。
(2)連接B D,設B D與A C交于點O,連接O P,O顯然平分B D,取S P的中點M。因為S D=3P D,所以S M=MP=P D。因此,BM∥O P,BM?平面P A C,所以BM∥平面P A C。同理ME∥平面P A C。因為BM∩ME=E,所以平面BME∥平面P A C。又B E?平面BME,故B E∥平面P A C。
4 4.(1)如圖1,過點M作ME∥C D交P D于E點,連接A E。因為AN=NB,所以AN=A B=D C=EM。又EM∥D C∥A B,所以EMAN,所以A EMN為平行四邊形,所以MN∥A E,所以MN∥平面P A D。
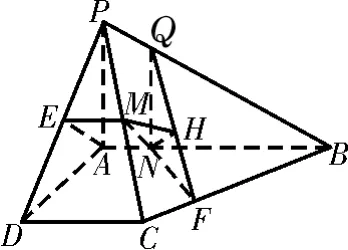
圖1
(2)如圖1,過N點作NQ∥A P交B P于點Q,NF⊥C B于點F,連接Q F,過N點作NH⊥Q F于點H,連接MH,易知QN⊥面A B C D,所以QN⊥B C。而NF⊥B C,所以B C⊥面QNF,所以B C⊥NH。而NH⊥Q F,所以NH⊥平面P B C,所以∠NMH為直線MN與平面P C B所成的角。

(2)點Ak的坐標為(-k,2),則S△AkF1F2=×FF×2=×6 3×2=6 3。122
(3)若k≥0,由62+02+1 2k-0-2 1=1 5+2k>0可知點(6,0)在圓Ck外;
若k<0,由(-6)2+02-1 2k-0-2 1=-1 5-1 2k>0可知點(-6,0)在圓Ck外。所以不論k為何值圓Ck都不能包圍橢圓G。
4 6.(1)取棱B B1的中點M,連接EM,C1M,因為E為棱A A1的中點,G為棱C1D1的中點,且A B=A D=1,C D=C C1=2,所以直四棱柱A B C D-A1B1C1D1中,EM∥A1B1∥CD且EM=AB=CD=CG。所1111111以四邊形EMC1G是平行四邊形,所以E G∥C1M。又因為E G?平面F C1C,C1M?平面F C1C,所以E G∥平面F C C1。
(2)直四棱柱A B C D-A1B1C1D1中,∠B A D=∠A D C=9 0°,所以 A D⊥ 平面DD1C1C。又因為E G∥平面F C C1,A B∥平面DD1C1C,B1B∥平面DD1C1C,所以VE-FC1C=VG-FC1C=VF-GC1C=VB-GC1C=VA-GC1C=×A D×S=×1××1×2=。△GC1C4 7.(1)依題意得a=2,以橢圓方程為+=1。將 (-,)代入y=x+m得直線l方程為y=x+1,將y=x+1與+=1聯立得(b2+4)x2+8x+4-4b2=0,則Δ=6 4-4(b2+4)(4-4b2)>0。

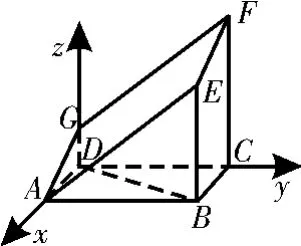
4 8.(1)在△B A D中,因為A B=2A D=2,∠B A D=6 0°,由余弦定理可得B D=3。所以A B2=A D2+B D2,所以A D⊥B D。又在直平行六面體中,G D⊥平面A B C D,所以G D⊥B D。又A D∩G D=D,所以B D⊥平面A D G。
(2)以D為坐標原點,建立如圖2所示的空間直角坐標系D-x y z。因為∠B A E=∠G A D=4 5°,A D=2A D=2,則 有A(1,0,0),B(0,,0),G(0,0,1),E(0,3,2),C(-1,,0)。所 以=(-1,3,2),=(-1,0,1)。設平面A E F G的法向量為n=(x,y,z),由


4 9.(1)因為A B C D-A1B1C1D1是長方體,所以平面A1A B∥平面C DD1C1。因為A1B?平面A1A B,A1B?平面C DD1C1,所以A1B∥平面C DD1C1。
(2)設A1A=h,因為幾何體A B C DACD的體積為,所以V=111ABCD-A1C1D1V-V=,即 S×A B C D-A1B1C1D1B-A1B1C1面ABCDh-×S×h=,即2×2×h-△A1B1C1××2×2×h=,解得h=4。所以A1A的長為4。
(3)如圖3,連接D1B,設D1B的中點為O,連接O A1,O C1,O D。因為A B C DA1B1C1D1是長方體,所以A1D1⊥平面A1A B。因為A1B?平面A1A B,所以A1D1⊥AB。所以O A=DB。111同理O D=O CDB。所以11O A1=O D=O C1=O B。所以經過A1,C1,B,D四點的球的球心為點O。因為D1B2=A1D12+A1A2+A B2=22+42+22=2 4。所以S球=4 π×(O D1)22=4 π× ()=π×D1B2=2 4 π。故經過A1,C1,B,D四點的球的表面積為2 4 π。
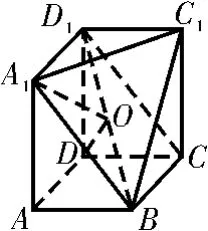
圖3


(責任編輯 劉鐘華)

