男女相親的最優配對問題

◎袁淑娟

男女相親的最優配對問題

◎袁淑娟

隨著社會的發展，相親已成為很多人尋找配偶的一種選擇。婚姻介紹所面對大量男士和女士，在了解他們的個人情況以及對對方的基本要求后，如何給他們配對才能使成功率最高就是一個亟需解決的問題。本文根據實際情況建立評價標準，得到男女相互間的評分表，然后利用匈牙利算法，計算出男女的最優配對組合，使得相親的總體成功率最高。

問題描述

相親已成為男女交友中較為流行的方式，其中大量相親是通過婚姻介紹所之類的機構組織的。我們假設婚介所了解了10對男女的個人情況（年齡，身高，體重，容貌，學歷，工作，家庭情況），以及他們對對方的要求（要求也是限制在這7個方面）。根據這些情況，婚介所該如何給這10對男女配對，才能使成功配對的人數最多。

模型的建立與求解

1） 處理數據，分析男女彼此滿意度

記 10位 女 士 分 別 為：w1，w2，w3…，w10，10位男士分別為：m1，m2，m3…，m10。先從女士w1開始，根據她在7個方面對對方的要求，逐一對10位男士進行評價打分，最后將得分相加，即該女士對該男士的評分，分數越高表示滿意度越高。結合實際情況，評價分為非常符合、比較符合、一般符合、不太符合和一定不行五種標準。為了量化處理，五種標準對應的數值如下表：

非常符合 比較符合 一般符合 不太符合 一定不行8 6 4 2 0

女士w1對10位男士的評價表：

w1 年齡 身高 體重 容貌 學歷 工作 家庭情況 總分m1 8 8 8 6 4 2 4 40 m2 8 8 8 8 8 8 8 56 m3 6 8 8 6 6 6 6 46 m4 6 4 4 6 2 2 4 28 m5 6 6 4 8 2 4 4 34 m6 8 6 6 6 0 2 4 0 m7 2 2 2 2 2 2 2 14 m8 8 6 2 4 2 4 6 32 m9 8 2 4 2 4 2 2 24 m10 8 8 6 8 8 8 6 52

根據實際情況，我們規定如果表中某一項評價為0分，則總分為0分。

同樣方式得到其余9位女士對10位男士的評價表，將總分匯總，得到10位女士對10為男士的評分表（表1），如下：

表中的數據表示所在列的女士對所在行的男士的評價總分。

同樣得到10位男士對10位女士的評分表（表2），如下：

表1

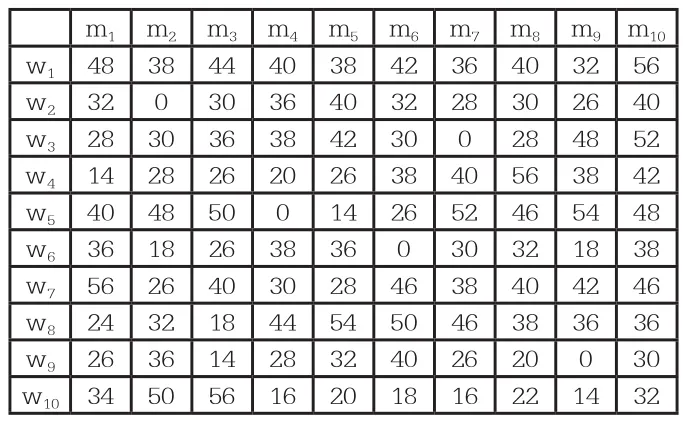
表2

將表1和表2的數據分別記為矩陣A和B，其中矩陣A中的數據Aij表示女士 wi對男士mj的評分，矩陣B中的數據Bij表示男士mi對女士wj的評分。記，則Eij表示女士wi與男士mj的互評分的平均值，Eij值越大，說明wi與mj的相互滿意度越高，兩位配對成功的概率越大。特別地，若A或BT中有一項數據為0，則E中對應數據為0。這是符合實際情況的，因為若A或BT中有一項數據為0，說明有一方對另一方一定不滿意，那么他們配對就不可能成功，所以E中對應數據為0。

2）建立模型并求解

要解決婚介所如何安排才能使配對成功的人數最多這一問題，只需要找出在矩陣E中的10個不同行不同列的元素，使其總和最大。顯然，這是一個指派問題，我們運用匈牙利算法求解。算法如下：

第一步，找出矩陣E中的最大值，然后用最大值減去矩陣E中的每一個元素得到新矩陣F，這樣就轉化為指派問題的標準形式，即求矩陣F中10個不同行不同列的元素，使其總和最小;

第二步，將矩陣F中的每一行元素減去此行中的最小元素，得到新矩陣F1;

第三步，從矩陣F1中只能選出6個不同行不同列的零元素，最優指派還無法看出，此時按照如下步驟進行：（1）對未選出0元素的行打√；（2）對√行中0元素所在列打√；（3）對√列中選中的0元素所在行打√。重復（2），（3）直到無法再打√為止。

第四步，用直線畫出沒有打√的行和打√的列，就得到了能夠覆蓋住矩陣中所有0元素的最小條數的直線集合，找出未覆蓋的元素中的最小者，令√行元素減去此數，√列元素加上此數，則原先選中的0元素不變，而未被覆蓋的元素中至少會有一個已轉變為0，得到新矩陣F1且新矩陣的指派問題與原問題也有相同的最優指派。

第五步，第三步和第四步反復進行，直到F1中能選出10個不同行不同列的0元素為止。

按照上述步驟計算，我們最終得到

該矩陣中已經可以選出10個不同行不同列的0元素（矩陣中已標記），這些0元素所在位置即最優指派，所以男女最優配對是 (M1,W3)、 (M2,W9)、 (M3,W10)、 (M4,W8)、(M5,W2)、 (M6,W7)、 (M7,W6)、 (M8,W4)、(M9,W5)、 (M10,W1)。

模型的推廣與評價

為了方便說明模型的情況，本文是為10對男女進行配對，在個人情況這方面給出了7個要求，但在Matlab運算軟件的幫助下，我們可以將人數和要求都提高至成千上萬，模型依然適用。并且在現實生活中有很多類似相親配對的問題，如公司招聘、學生就業等都可以用這個模型進行求解。

浙江經濟職業技術學院）