聯供系統在線尋優的遺傳算法軟件實現

江 兵，李 冰，黃振軍

（中國船舶重工集團公司第七一一研究所，上海 201108）

聯供系統在線尋優的遺傳算法軟件實現

江 兵，李 冰，黃振軍

（中國船舶重工集團公司第七一一研究所，上海 201108）

本文聚焦于實用型熱電聯供系統。為克服運行調度技術障礙，依據熱力學原理建立了聯供系統能效優化模型。利用聯供系統示范項目實測數據，通過回歸計算，并參考所用設備性能規格，確定了該優化模型參數。為適應優化模型非線性、多變量特點，對通用遺傳算法適當改進，并用 C#語言開發了智能優化軟件，解決了聯供系統上述優化模型在線求解難題。最后，用實際算例驗證了該遺傳算法優化軟件，在熱電聯供系統聯線優化調度中的應用價值。

計算機軟件；熱電聯供；能效優化；遺傳算法

0 引言

熱/電負荷之間不平衡變化，是熱電聯供系統的一對矛盾[1]，引發了機組運行調度困難、能效達不到預期、經濟效益下滑等一系列問題。采用圖（1）帶儲熱或蓄冷的熱電聯供方案，雖然可以緩解這對矛盾；但是，儲能裝置的投入給系統運行調度增加了難度[2]。隨著熱、電負荷的不平衡變化，聯供發電機組最佳輸出功率點的實時、在線、自動計算，成為熱電聯供系統運行控制環節面臨的難題[3]。

遺傳算法求解復雜非線性優化問題具有普適性[4]。盡管遺傳算法應用中還存在著局部搜索能力差和容易出現早熟現象等問題[5-9]；但是，以遺傳算法為基礎的隨機優化方法仍然是提高與聯供系統類似的復雜系統調度自動化水平、降低運行操作負擔的有效途徑[10-12]。

本文針對聯供系統能效優化模型特點，以及遺傳算法的優缺點，從編碼方案和遺傳算子開發等方面著手，采用通俗易懂的C#語言，和具有跨平臺運行優點的.NET技術，實現了聯供系統遺傳算法尋優技術。

1 熱電聯供系統結構特點

由天然氣內燃機組構成的熱電聯供系統如圖 1所示，其特點如下：

（1）機組缸套水余熱利用+容積水箱蓄熱。煙氣余熱單獨利用，不參與調度；

（2）機組輸出電功率和余熱功率之間的比例，與動態變化的熱/電負荷比不一致；

（3）系統熱負荷變化符合統計規律,可以預測。

2 能效優化原理

以系統熱負荷預測為基礎；以提高能效，降低天然氣消耗為優化目標；通過決策變量（燃氣機組運行功率）優化設置，來維持系統熱量供求關系動態平衡，避免冷卻回水溫度超限，提高機組利用率。尋優區間將根據機組容量和經濟負荷率確定。能效優化問題形式化描述如下：

（2）約束條件:機組冷卻回水溫度低于上限，即： Thi＜Tmax

（3）決策向量：未來若干時間段機組功率設定

3 能效優化模型實例

3.1 某型號燃氣發電機組天然氣消耗特性

3.2 某賓館春秋季熱電聯供系統熱負荷（時間序列）預測模型

熱負荷預測模型的階次和系數由實測數據通過辨識得到。

3.3 機組冷卻回水溫度數學模型

3.3.1 缸套水換熱器熱端出口溫度與冷端進口溫度之間的聯系

根據換熱器的傳熱方程 Pi= K× Sh×ΔTmi、熱端和冷端熱平衡方程可得換熱器熱端出口溫度與冷端進口溫度的換算關系：

3.3.2 蓄熱水罐熱量傳遞關系

蓄熱水罐既通過缸套水換熱器吸收熱量，又提供生活熱水釋放熱量；其換熱過程可以用如下方程描述：

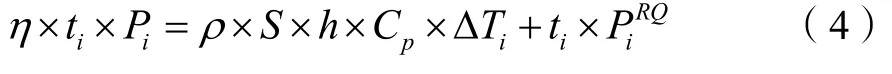
式中：η：蓄熱水罐熱損失系數；it：第i時段機組運行時間，s；S：水罐橫截面積，；h：蓄熱水罐水位，m；：蓄熱水罐第i時段熱負荷預測值，kW。

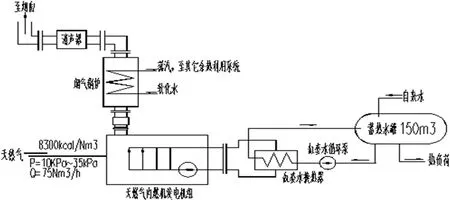
圖1 熱電聯供系統示意圖Fig.1 Cogeneration system schematic diagram

3.3.3 冷卻回水溫度的數學描述

式（3）既描述蓄熱水罐換熱過程，又反映熱電聯供系統熱量供需動態平衡。

綜合（2）、（3）式可得缸套水回水溫度（換熱器熱端出口溫度）與機組運行功率、系統熱負荷之間關系如下：

3.3.4 不等式約束條件及處理方式

為保證發電機組穩定運行,提高機組利用率，必須限制缸套冷卻水回水溫度，以避免機組因超溫保護而意外停機。因此要求由（4）式得：

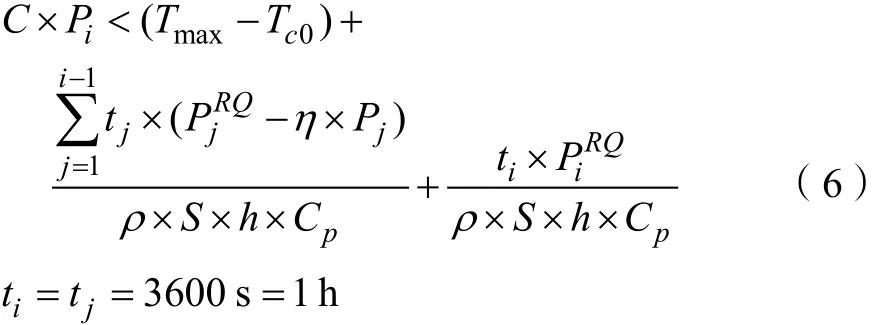
Tc0：起點時刻換熱器冷端入口溫度（即：蓄熱水罐溫度），此前各時段蓄熱水罐熱負荷與輸入熱量差額的累積（可測參數），kJ。

如果對所討論的熱電聯供系統進行提前2 h的優化調度，并對熱負荷作2步預測（每步時長為1 h），則在蓄熱水罐已蓄熱 30.00 kWh，并且系統熱負荷 2步預測值分別為=200 kW前提下，將表1中工藝參數帶入（5）式，可得熱電聯供系統能效優化模型約束條件的參數化實例如下：

式（6）所示能效優化模型約束條件實例為不等式。為便于求解，必須對式（6）作進一步處理。

采用“松弛變量”（松弛系數：0.05），可將不等式約束（6）轉化為等式約束（7），以便優化模型的后續求解。

采用“懲罰函數”，可消除優化模型中的等式約束，從而將原優化問題進一步轉換為不含約束條件的經典優化問題來求解。具體方法：通過權重系數將約束等式與原目標函數組合，重新構造等價的目標函數（8）。轉換后的目標函數最優解將逼近原優化問題的最優解。

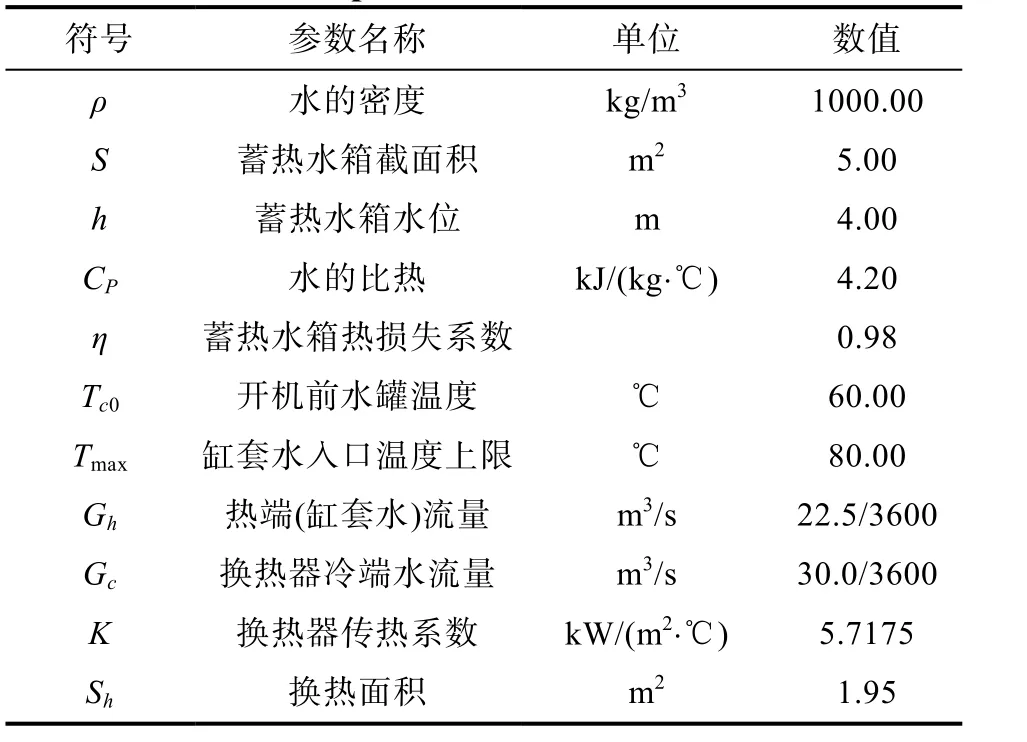
表1 熱電聯供系統工藝參數Tab.1 Cogeneration system technological parameter table

3.3.5 等效目標函數

經過以上處理，與原熱電聯供系統能效優化問題等效的無約束優化問題目標函數為：

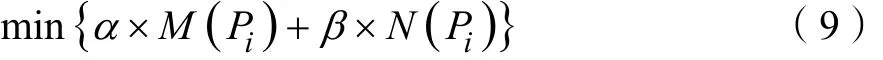
天然氣發電機組額定容量為300 kW，經濟運行功率下限為150 kW，決策分量的取值范圍為[150, 300]。

4 遺傳算法尋優的軟件實現

遺傳算法實現過程需要設計：編碼方案、選擇策略和遺傳算子。

4.1 編碼方案

采用二進制編碼，將整數格式的2個決策分量分別轉換成二進制編碼，再連接成長串二進制碼序列。決策變量尋優空間為實數[150.0,300.0]之間。偏移-150.0后，待編碼的搜索變量取值范圍為整數[0，150]之間。為了提高計算精度，搜索變量分別乘10倍，取值范圍相應擴大為 0～1500。由于 210能表示的無符號整數范圍為0～1024，因此單個搜索變量的二進制編碼長度至少為11位，所以2個搜索變量連成串后的二進制編碼長度為22位。

4.2 選擇策略

采用“比例選擇算子”。設計思想：單個個體被選中的概率與其適應度成正比。如果種群規模為n，個體i的適應度為fi，則個體i被選中的概率Pi為：

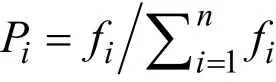
4.3 遺傳算子

采用單點交叉。雜交個體、交叉換位點和變異點都隨機選擇。雜交概率和變異概率在人機界面設置。交叉換位和變異算法，充分利用了C#語言移位和位邏輯運算指令簡潔、高效的優勢。

4.4 適應值函數

式（9）作為優化問題的目標函數，需要求的是最小值；而適應值函數通常求最大值。為此，將式（9）改寫成式（10）形式:

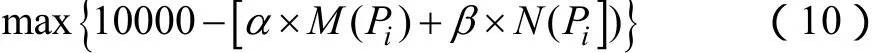
4.5 聯供系統遺傳算法尋優的C#語言關鍵源代碼

public class CsGaClass //遺傳算法基因類

{

public int PopulationSize; //種群規模

private int CodeSize; //編碼長度

public double CrossProbab; //交叉概率

public double MutantProbab; //變異概率

public int[] Popula; //種群

public double Alpha; //權重

public double Belta;

······

public void FitComput() //適應值計算

{

for (int i = 0; i ＜ PopulationSize; i++)

{

·····

mx=0.0007086*System.Math.Pow(p1,2)-0.09694*p1+32.65+0.0007086*System.Math.Pow(p2,2)-0.09694*p2+32.65;

nx=System.Math.Pow(0.085*p1-24.293,2)+System.Math.Pow(0.042*p1+0.085*p2-32.436,2);

Fit[i] = 10000-(Alpha * mx + Belta * nx) ;//適應值公式

}

}

public void PopulaSelect() //選擇算子

{

double sel; //[0，1]之間均勻分布的隨機數，用于輪盤賭

·····

for (int i = 0; i ＜ PopulationSize; i++)

{

sel = autoRand.NextDouble();

if (sel ＜ accselpro[0])

TransitPopula[i] = Popula[0];

for (int j = 1; j ＜ PopulationSize; j++)

{

if (( accselpro[j - 1] ＜= sel) && (sel ＜accselpro[j])) //輪盤賭

{

TransitPopula[i] = Popula[j];

break;

}

}

}

}

public void PopulaCross() //交叉算子

{

·····

while ( i ＜ (int)( crosscount/2 ) )

{

cross

point=(int)(CodeSize*autoRand.NextDouble()); //隨機確定交叉位

tp11 = anticrossmask & cross[2 * i];

tp12 = crossmask & cross[2 * i]; //與掩碼逐位與，交叉位分離

tp21 = anticrossmask & cross[2 * i + 1];

tp22 = crossmask & cross[2 * i + 1];

cross[2*i] = tp11 | tp22; //逐位邏輯或，完成交叉互換

cross[2*i+1] = tp21 | tp12;

}

}

public void PopulaMutant() //變異算子

{

·····

while(i＜mutantcount)

{

l =(int)(PopulationSize*autoRand.NextDouble());

tp = TransitPopula[l]; //隨機確定基因變異個體

mutantpoint=(int)(CodeSize*autoRand.Next

Double());//隨機定變異位

if (( tp & mutantmask ) != 0 ) //基因變異

tp &= antimutantmask;

else

tp |= mutantmask;

}

}

}

4.6 遺傳算法與遍歷搜索算法的比較

為比較算法性能優劣，首先采用基本的遍歷搜索算法求解上述優化問題。當 a=b=0.5時，遍歷搜索算法求得的精確最優解：P1=273.5,P2=230.6。

當算法關鍵參數取下圖所示經驗值，同樣在a=b=0.5條件下，用遺傳算法求解上述熱電聯供系統能效優化問題的實測計算性能為：誤差＜1.0%的命中概率＞95.6%。因此，所實現的遺傳算法穩定性和計算精度2項衡量指標都可以滿足工程實際需要。

采用遺傳算法求解上述能效優化問題，平均耗時 0.88 s；而在同一臺計算機上，采用遍歷算法搜索同樣的尋優空間,平均耗時0.63 s。所以，在上述優化問題尋優空間內搜索，遍歷算法雖然略微領先，但不具備突出優勢。一旦搜索范圍擴大至n倍，則遍歷算法求解時間將增長至n2倍。而遺傳算法求解時間僅受遺傳代數影響略大，并且時間增長與遺傳代數增加呈線性比例關系。更為重要的是，下圖所示遺傳算法相關參數已經優化，搜索空間擴大后無須通過增加遺傳代數來減小誤差或提高命中概率；因此，計算時間不會明顯增加。所以，用遺傳算法解決上述熱電聯供系統能效優化問題優勢明顯。

圖2 遺傳算法參數設定界面Fig.2 Genetic algorithm parameter setting interface

5 結論

本文根據一種熱電聯供系統結構建立的能效優化調度模型，不僅重點圍繞實際應用中存在的問題而設置優化目標和約束條件，而且模型參數計算也建立在實際測量或工程設計計算基礎上，具有切合實際的應用背景，對解決同類熱電聯供系統運行調度和優化控制問題具有良好的參考價值和借鑒意義。

所開發的遺傳算法尋優程序，在計算精度和穩定性方面已得到遍歷搜索算法驗證。計算速度相對穩定的優勢也表明，遺傳算法比較適合實際工程應用。

[1] 馬瑞, 李文曄, 李晅, 等. 分布式冷熱電聯供系統負荷隨機模糊建模[J]. 電力系統自動化. 2016, 40(15): 53-58.MA R, LI W Y, LI X, et al. Random Fuzzy Model for Load of Distributed Combined Cooling Heating and Power System[J]. Automation of Electric Power Systems, 2016, 40(15):53-58. (in Chinese)

[2] 陸偉, 張士杰, 肖云漢. 有蓄冷器的聯供系統優化運行[J].中國電機工程學報. 2007, 27(8): 49-53. LU W, ZHANG S J,XIAO Y H. The Optimal Operational Planning of a Cogeneration System With Storage[J]. Proceedings of the CSEE,2007, 27(8): 49-53. (in Chinese)

[3] 王成山, 武震, 李鵬. 微電網關鍵技術研究[J]. 電工技術學報. 2014, 29(2): 1-12.WANG C S, WU Z, LI P. Research on Key Technologies of Microgrid [J]. Transactions of China Electrotechnical Society,2014, 29(2): 1-12. (in Chinese)

[4] 楊啟文, 蔣靜坪, 張國宏. 遺傳算法優化速度的改進[J].軟件學報. 2001, 12(2): 270-275.YANG Q W, JIANG J P, ZHANG G H. Improving Optimization Speed for Genetic Algorithms[J]. Journal of Software,2001, 12(2): 270-275. (in Chinese)

[5] 邊霞, 米良. 遺傳算法理論及其應用研究進展[J]. 計算機應用研究. 2010, 27(7): 2425-2429.BIAN X, MI L. Development on genetic algorithm theory and its applications[J]. Application Research of Computers,2010, 27(7): 2425-2429. (in Chinese)

[6] 朱臻, 何清頂, 張博. 大規模測控資源規劃問題的改進遺傳算法研究[J]. 軟件, 2013, 34(2): 82-83.ZHU Z, HE Q D, ZHANG B. An Improved GA to Solve Large Scale TT & C Resource Scheduling Problem[J].Software, 2013, 34(2) : 83-83. (in Chinese)

[7] 薄鈞戈, 蘇紅旗. 一種基于遺傳算法的排課方法研究[J].軟件, 2014, 35(1): 43-45.BO J G, SU H Q. One Study on the Genetic Algorithms for the Timetabling Problem[J]. Software, 2014, 35(1): 43-45.(in Chinese)

[8] 水勇. 遺傳算法的研究與應用[J]. 軟件, 2014, 35(3): 107.SHUI Y. The Research and Application of Genetic Algorithm[J]. Software, 2014, 35(3): 107. (in Chinese)

[9] 聶敬云, 李春青, 李威威, 等. 關于遺傳算法優化的最小二乘支持向量機在MBR 仿真預測中的研究[J]. 軟件,2015, 36(5): 40-44.NIE J Y, LI C Q, LI W W, et al. Research on the Least Squares Support Vector Machine Optimized by Genetic Algorithm in the Simulation MBR Prediction[J]. Software,2015, 36(5): 40-44. (in Chinese)

[10] 李杰煌, 栗元邦. 基于遺傳算法的民航機組排班系統[J].軟件, 2013, 34(4): 38-39.LI J H, LI Y B. Civil aviation units scheduling system based on genetic algorithm [J]. Software, 2013, 34(4): 38-39. (in Chinese)

[11] 謝佩軍. 一種基于膜計算的遺傳算法圖像分割方法[J]. 軟件, 2014, 35(9): 80-85 XIE P J. A GA-Based Image Segmentation Using Membrane Computing[J]. Software, 2014, 35(9): 80-85. (in Chinese)

[12] 陳曉燕, 姚高偉, 張鯤, 等. 基于遺傳算法的無線傳感器節點定位在農業的應用[J]. 軟件, 2015, 36(4): 1-5.CHEN X Y, YAO G W, ZHANG K, et al. The Application of Wireless Sensor Node Localization Based on Genetic Algorithm in Agriculture[J]. Software, 2015, 36(4): 1-5. (in Chinese)

Software Implementation of Genetic Algorithm for Cogeneration System Online Optimization

JIANG Bing, LI Bing, HUANG Zhen-jun
(Shanghai Marine Diesel Engine Research Institute, Shanghai 201108, China)

This paper focuses on the commonly used cogeneration system. Based on the thermodynamics principle, the cogeneration system energy efficiency optimization model is established to resolve the difficulty in the system scheduling. The parameters of the optimization model are determined by regression calculation of the measured datas and consulting the performance specifications of the equipments used in the demonstrative cogeneration system. For adapting the nonlinear and multi-variable characteristics of the optimization model, the general genetic algorithm is improved appropriately. Using C# language, the intelligent optimization software is developed at the same time for solving the cogeneration system online optimization problem. Finally, the application value of the genetic algorithm optimization software for cogeneration system optimal scheduling is verified by a practical example.

Software; Cogeneration; Optimization of energy efficiency; Genetic algorithm

TP273+.1

A

10.3969/j.issn.1003-6970.2017.12.040

本文著錄格式：江兵，李冰，黃振軍. 聯供系統在線尋優的遺傳算法軟件實現[J]. 軟件，2017，38（12）：206-210

江兵(1967-)，男，高級工程師，主要研究方向為：發動機控制、分布式能源控制和可再生能源優化調度技術；李冰(1966-)，男，高級工程師，主要研究方向為：內燃機、分布式供能和可再生能源技術；黃振軍(1975-)，男，高級工程師，主要研究方向為：特種發動機控制、軟件、人工智能。