基于DCT零系數和局部標準差的自動聚焦算法

呂美妮，玉振明

(1.桂林電子科技大學 信息與通信學院，桂林 541004；2.梧州學院 廣西高校圖像處理與智能信息系統重點實驗室，梧州 543002)

基于DCT零系數和局部標準差的自動聚焦算法

呂美妮1，玉振明2*

(1.桂林電子科技大學 信息與通信學院，桂林 541004；2.梧州學院 廣西高校圖像處理與智能信息系統重點實驗室，梧州 543002)

聚焦評價函數的設計與選取是顯微鏡自動聚焦的核心問題之一,光照變化引起函數曲線失去理想特性，傳統的聚焦評價函數無法克服這一問題。為了解決此問題，提出一種結合頻域離散余弦變換(DCT)零系數和空域局部標準差的自動聚焦算法。通過計算圖像子塊的DCT高頻零系數個數和局部標準差，利用兩者相反的作用效果進行除法運算，并采用平方運算加大該算法的清晰度比率，在不同光照條件下，與幾種傳統的聚焦評價函數進行聚焦對比實驗，驗證了該算法的適用性，并對聚焦評價函數使用定量指標進行性能評估。結果表明，該算法在低照度的條件下還能保持良好的曲線特性，并且具有較強的抗噪性、靈敏度和穩定性。

圖像處理；自動聚焦；聚焦評價函數；離散余弦變換零系數；局部標準差

引 言

聚焦是顯微鏡成像系統的重要環節，常用的聚焦方法主要分為焦點檢測法、測距法和圖像處理法3種[1]。相比于焦點檢測法和測距法，基于數字圖像處理的自動聚焦技術具有智能化、快速準確、控制方便等特點，成為近年來研究的熱點[2-3]。其中，聚焦評價函數的選取是基于數字圖像處理的自動聚焦技術的核心問題之一，它直接決定聚焦的準確性。目前已有的聚焦評價函數主要分為3類：頻域類函數、梯度類函數和統計類函數[4-5]。在光照強度適宜的條件下，顯微鏡采集的圖像對比度高，細節更明顯，上述的聚焦評價函數均能滿足聚焦的要求；但遇到光照強度較弱的條件下，上述的聚焦評價函數大多會失去原來的理想曲線特性，造成聚焦的不準確性。低照度的顯微圖像，對比度低、噪聲大、圖像整體和細節辨識度較低，加大聚焦的難度。雖然可以通過提升對比度、低通濾波器等方式減弱光強對聚焦的影響，但圖像方法拉伸對比度也會增加額外的噪聲、低通濾波器的選擇不當也會造成濾波不足使得噪聲依然存在或者濾波過度使得原本有用的高頻信息被消除的問題[6]。

大多數傳統聚焦評價函數不能克服光照變化帶來的不利影響，針對此問題，本文中提出一種基于離散余弦變換(discrete cosine transform，DCT)零系數和局部標準差的聚焦算法，該算法結合頻域DCT零系數和空域局部標準差，在光照變化的條件下，還能保持良好的聚焦特性，適用于顯微鏡成像系統。

1 傳統聚焦函數和性能評價指標

實現高精度的自動聚焦是顯微鏡自動化的首要問題之一[7]，其關鍵是確定評價聚焦評價函數的定性指標。一個理想的聚焦評價函數應滿足單峰性、無偏性、高靈敏性和抗噪性[8]。

1.1 傳統聚焦函數

本節中列舉的5種聚焦函數用于后續的對比實驗，其中F為聚焦評價函數值，f(x,y)為圖像點(x,y)的灰度值，圖像大小為M×N。

(1)灰度差分絕對值和(sum modulus difference， SMD)函數[9]:

(2)方差函數[10](variance函數):

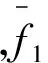
(3)基于Robert算子的差分絕對值和函數[11](簡稱Robert函數):

(4)基于Sobel算子的函數[12](簡稱Sobel函數):

式中,gx(x,y)和gy(x,y)分別表示圖像與水平和垂直Sobel算子Sx和Sy的卷積。

(5)離散傅里葉變換(discrete Fourier transform，DFT)函數[13]:

式中,f(u,v)為圖像進行離散傅里葉變換后的頻率系數矩陣。

1.2 性能評價指標

評價聚焦評價函數性能的好壞，除了定性指標(單峰性、無偏性、高靈敏度和抗噪性)還應結合定量指標，定量指標更能客觀地體現不同聚焦評價函數的差異。

(1)清晰度比率R

清晰度比率R表征聚焦評價函數對不同離焦程度圖像的分辨能力[12]。R越大，聚焦圖像和離焦圖像清晰度值的差異越大，越容易區分。

式中,Fmax和Fmin聚焦函數的最大值和最小值(最小值應在聚焦曲線的平緩區取得)。

(2)靈敏度因子S

靈敏度因子S表征聚焦評價函數最大值附近變化的劇烈程度[12]。對于不同的聚焦評價函數，靈敏度因子越高，則該函數適用于細聚焦階段。

式中，x1為橫坐標變化量，xmax為函數最大值的橫坐標。

(3)平緩區波動量V

受噪聲的影響，平緩區的聚焦評價函數值并不是單調遞增或遞減，而是呈現出一種波動狀態[14]，波動越平緩，說明該函數的抗噪性較強。首先假設采樣點有N個(曲線的平緩區取得)，則定義N個點的函數值標準差為平緩區波動量。

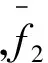
2DCT零系數和局部標準差結合的聚焦評價函數

2.1 理論知識

2.1.1 DCT零系數 圖像經過DCT變換后的DCT系數矩陣體現了圖像頻率的分布情況。對于任意的圖像進行DCT變換，得到一個2維矩陣F1(u,v)，隨著u和v的增大，對應的DCT系數也不斷增大。DCT系數主要分為低頻系數、中頻系數和高頻系數3種。在圖像局部模糊檢測中，由于模糊區域邊緣信息較少，導致高頻系數為零的個數較多；而內容豐富的清晰區域，高頻零系數個數較少[15]。在此理論基礎上，可以發現在聚焦的過程中，內容子塊經歷了模糊→清晰→模糊這樣一個過程，其對應的高頻零系數的個數發生相應的變化。而背景子塊在聚焦過程基本上無變化，故其對應的高頻零系數個數基本上不變。

選中的圖像子塊位置如圖1a所示，圖1b為相同位置的子塊在聚焦過程中DCT零系數個數的變化曲線圖。從圖1b中可以看出，內容子塊的DCT零系數在聚焦位置個數最少，且曲線變化和理想的聚焦評價函數曲線有相同的特性，但唯一的區別是，曲線最小值點為圖像聚焦位置。背景子塊的DCT零系數個數在一定的范圍內波動，且內容子塊的DCT零系數個數變化曲線的平緩區也出現一定的波動，這是受圖像子塊中噪聲的影響，引起誤判造成的，但不影響后續算法中應用。

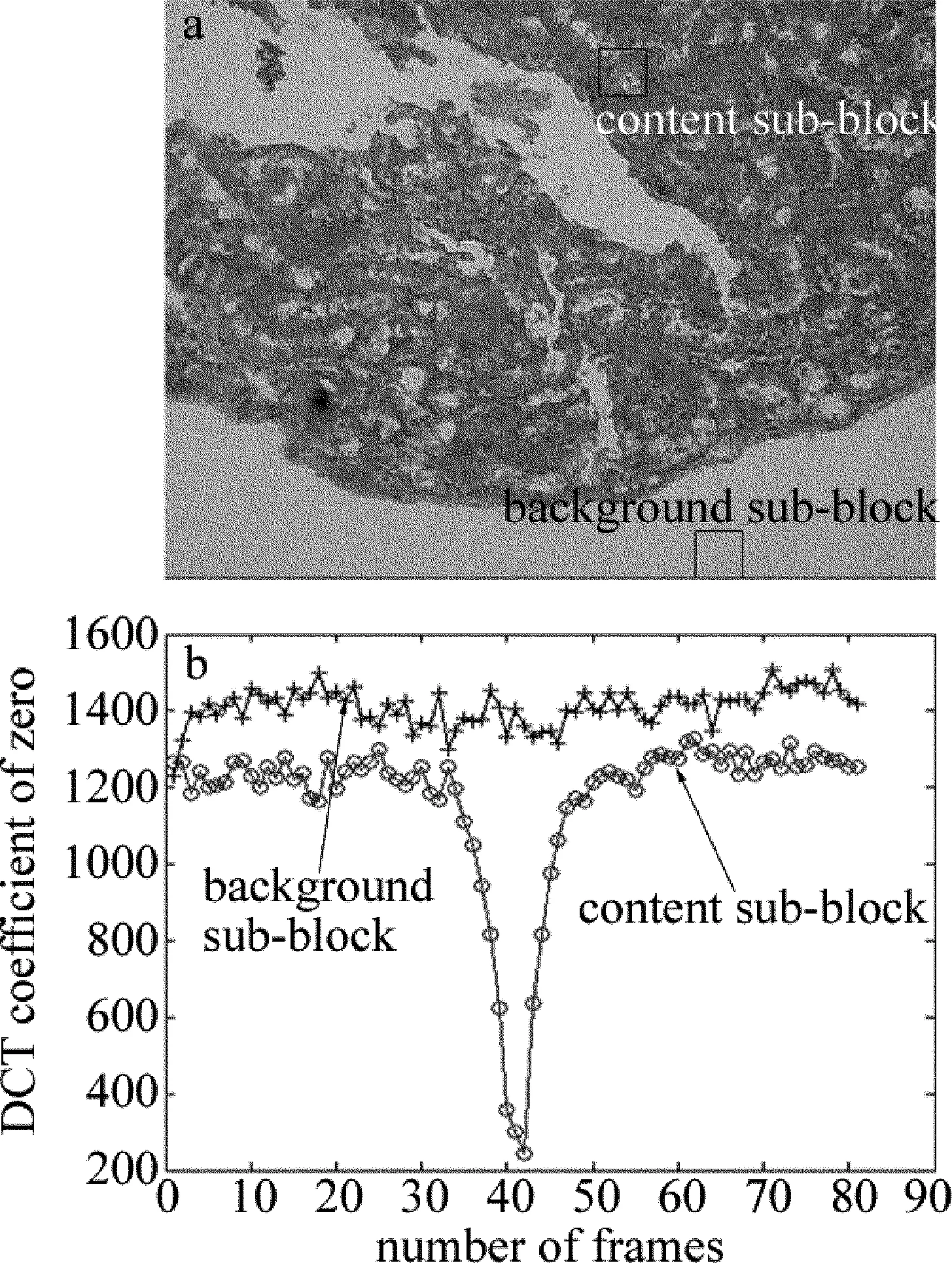
Fig.1 a—the positions of sub-blocks b—the curves of DCT coefficient of zero of the sub-blocks

圖1b中，內容子塊的DCT零系數個數變化明顯，而背景子塊的DCT零系數個數則在一定的范圍內波動，故圖像所有子塊的DCT零系數個數相加之和，可作為聚焦評價函數，其最小值點即為聚焦位置。

2.1.2 局部標準差 局部標準差反映圖像局部灰度值的變化程度[16]。在圖像局部模糊檢測中，一般用于單個像素點的判斷。圖像分為模糊區域和清晰區域，模糊區域包含較少的邊緣信息，灰度變化緩慢，故局部標準差較小；而清晰區域包含較多的邊緣信息，灰度變化劇烈，一般具有較大的局部標準差。同樣的道理，在聚焦的過程中，內容子塊經過了模糊→清晰→模糊的過程，故可以推斷，在此過程中，內容子塊的局部標準差也發生相應的變化，且在聚焦位置內容子塊的局部標準差最大。而背景子塊灰度值基本不變[17],故背景子塊的局部標準差也基本不變。

選中的圖像子塊位置如圖2a所示，圖2b為相同位置的子塊在聚焦過程中局部標準差的變化曲線。從圖2 可以看出，在聚焦的過程中，內容子塊的局部標準差變化劇烈，最清晰圖片對應的位置為曲線最大值處，滿足聚焦曲線的特性。而背景子塊的局部標準差在一定的范圍內基本不變，故圖像所有子塊的局部標準差之和也可作為聚焦評價函數，其曲線最大值點即為聚焦位置。

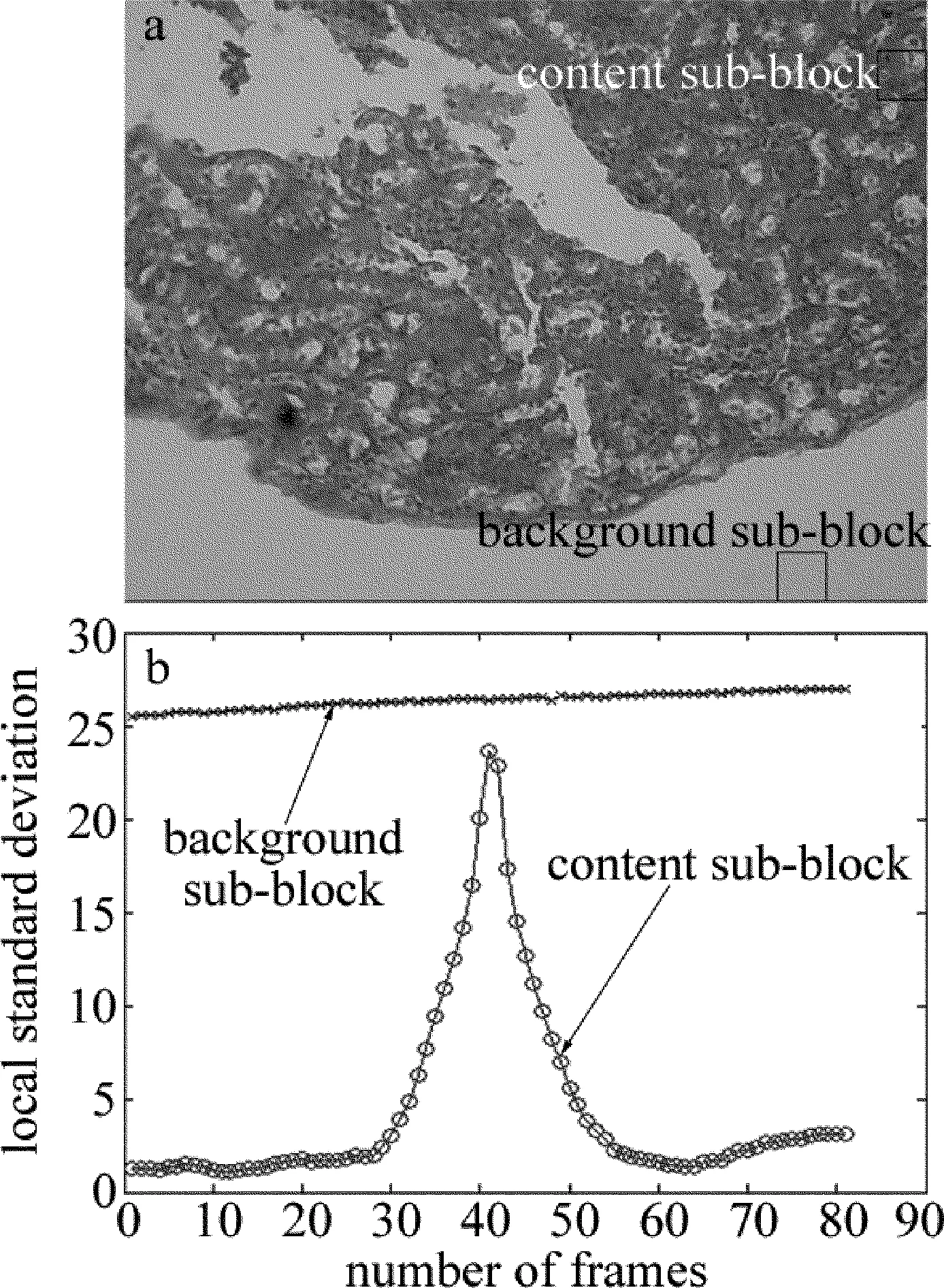
Fig.2 a—the positions of sub-blocks b—the curves of local standard deviation of the sub-blocks

2.2 聚焦函數

對大小為M×N的圖像進行分塊，將其劃分為m×n個圖像塊，子塊大小為w×w，其中m=M/w，n=N/w。(i,j)為圖像子塊位置，f(x,y)為圖像點(x,y)的灰度值。

(1)對圖像子塊進行DCT變換:

F2(u,v)=c(u)c(v)×

式中,

(2)統計子塊(i,j)內DCT零系數個數:

(3)求子塊(i,j)的局部標準差:

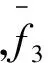
(4)在聚焦的過程中，圖像子塊的DCT系數個數和局部標準差發生劇烈的變化，DCT零系數個數與局部標準差的變化正好相反，利用這個特性，組建新的聚焦函數，并進行平方運算來加大函數的清晰度比率，公式如下：

在聚焦的過程中，子塊的DCT零系數個數變化如圖1b所示，而子塊的局部標準差的變化如圖2b所示，當圖像最清晰時(最佳聚焦點)，此時相同位置的內容子塊的d(i,j)最小，σ(i,j)最大，則其對應的F最大；而相同位置的背景子塊的d(i,j)和σ(i,j)則在一定范圍內保持不變，則其對應的F在一定的范圍內平緩波動，故所有子塊的聚焦函數值F在圖像最清晰的情況下，處于最大值位置，符合聚焦函數曲線的特性，且聚焦的過程中，d(i,j)和σ(i,j)的作用效果相反，相除會使得函數作用效果更加明顯，更能區分離焦圖像和聚焦圖像的差異。在此過程中，背景子塊一直在一定的范圍內波動，作用不大，起決定性作用的是內容子塊，故一般先確定聚焦窗口，剔除背景子塊，使得聚焦效果更明顯。而本文中聚焦函數不僅能適用于對整幅圖像進行處理，且也具有理想聚焦曲線的一般特性。

3 聚焦函數仿真實驗及結果分析

本文中的實驗壞境為：CPU，Intel(R) Core(TM)i7-6700 3.4GHz；RAM，8.00GB；MATLAB(R2014a)。

實驗圖片(480×640)均通過梧州奧卡光學儀器公司研發的光學顯微鏡(XSZ-8100)進行采集。

3.1 仿真實驗1

驗證本文中函數的性能，對所提到的聚焦函數進行仿真實驗。實驗中采用如圖3、圖4所示的2組不同光照強度但內容相同的顯微圖像序列(離焦-聚焦-離焦)。為了便于觀察，圖像序列的最佳聚焦位置為第40幀。聚焦窗口的選取方法統一使用參考文獻[18]中提到的選取方法。

Fig.3 Defocus and focus images with light intensity of 6

Fig.4 Defocus and focus images with light intensity of 1

實驗仿真曲線如圖5所示。從圖5a可以看出，本文中聚焦評價函數和傳統的聚焦評價函數在光照穩定的條件下，均滿足單峰性和無偏性。當光照強度較弱的情況下，顯微圖像序列的噪聲大，圖像整體和細節辨識度較低。從圖5b中可以看出，在低照度的情況下，傳統聚焦評價函數的仿真曲線大多數出現了局部極值，且平緩區出現了波動，而本文中函數還能保持理想曲線的特性。故本文中函數適用于低照度的自動聚焦系統，且具有較強的抗噪性。

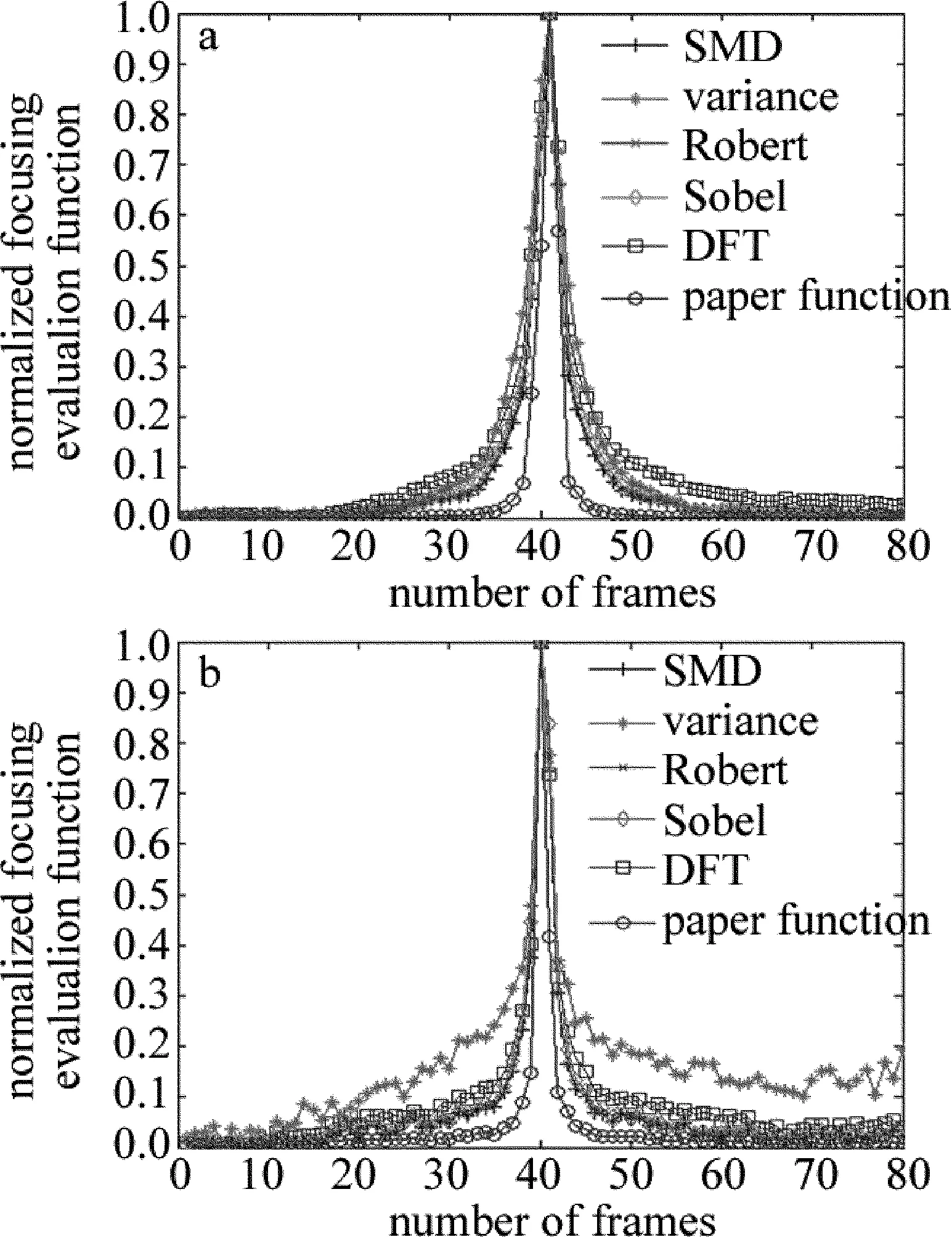
Fig.5 Simulation curves of focusing function

3.2 仿真實驗2

為了進一步驗證本文中函數的適用性，通過與傳統的聚焦函數進行再次聚焦對比實驗，實驗中采用2組低照度的顯微圖像序列(離焦-聚焦-離焦)如圖6、圖7所示。聚焦窗口的選取方法統一使用參考文獻[18]中所提到的選取方法。圖6所示的圖像序列的最佳聚焦位置在第74幀，圖7所示的圖像序列的最佳聚焦位置在第48幀。

Fig.6 Defocus and focus images with light intensity of 1.5

Fig.7 Defocus and focus images with light intensity of 2

此處需要說明是：(1)光照強度越弱，采集到的顯微圖像序列整體灰度值越低，對比度越低，且噪聲越大，對聚焦評價函數的影響也就越大，但由于光照強度低于1的情況下，即使能從肉眼能辨別圖片的聚焦位置，但本文中函數與傳統聚焦函數曲線均失去理想的曲線特性，故實驗中選取光照強度大于1的圖像序列;(2)考慮到選用低通濾波器不當有可能造成噪聲依然存在或濾除掉圖像的有用信息，造成聚焦的不準確，故不對圖像進行預處理;(3)對圖片不進行預處理噪聲依然存在，在實驗的過

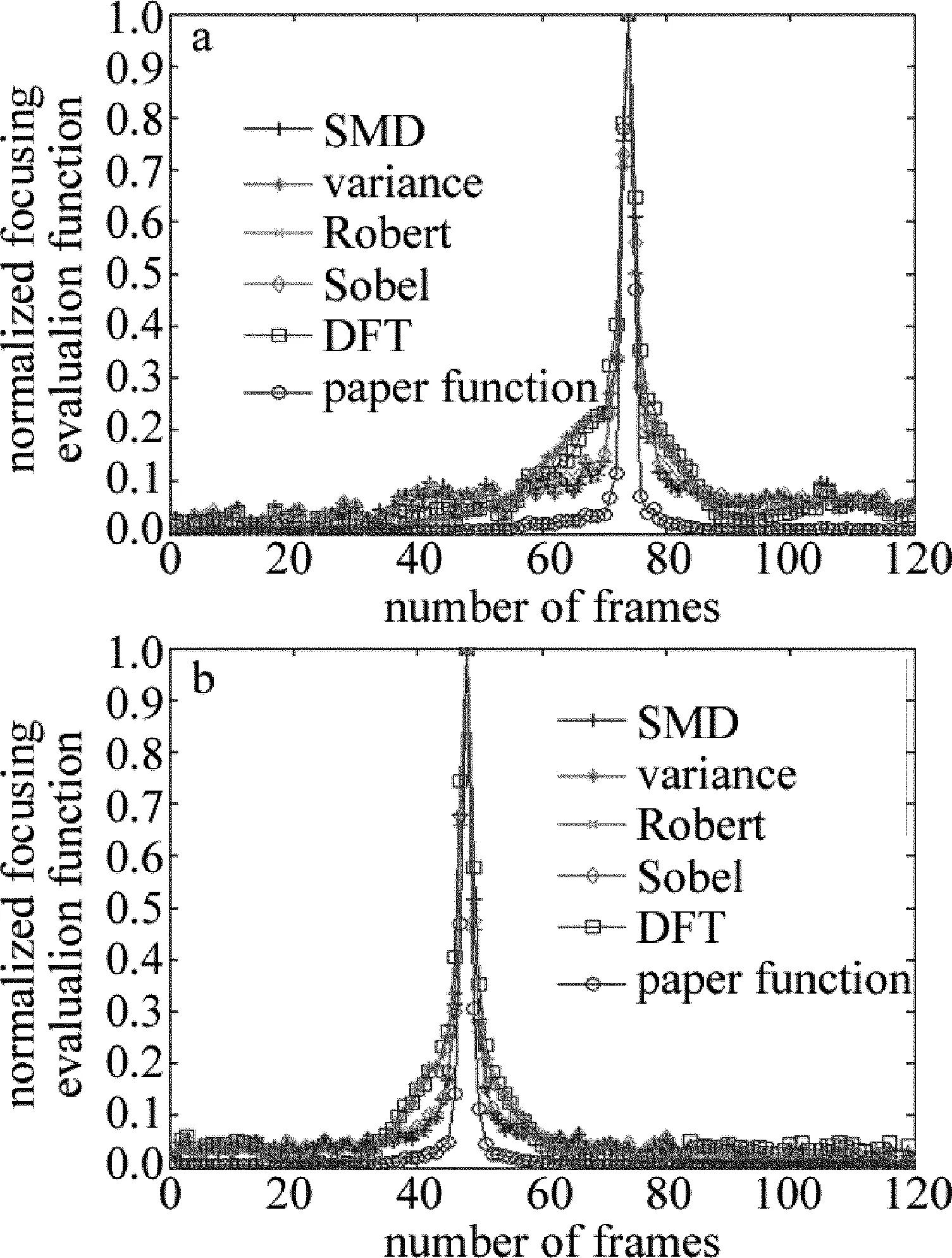
Fig.8 Simulation curves of focusing function

x

3.3 實驗結果分析

從實驗仿真曲線可以看出，本文中函數在低照度的情況下還能滿足理想聚焦曲線的特性，而傳統的聚焦評價函數在低照度的情況下，由于受噪聲的影響，平緩區出現波動，且隨著光照強度的增加，平緩區波動也逐漸平緩。

對進行實驗的聚焦函數進行定量分析。通過數據分析各函數的曲線特性。表1、表2中給出實驗2中，各函數的清晰度比率R、靈敏度因子S、平緩區波動量V和處理時間t。

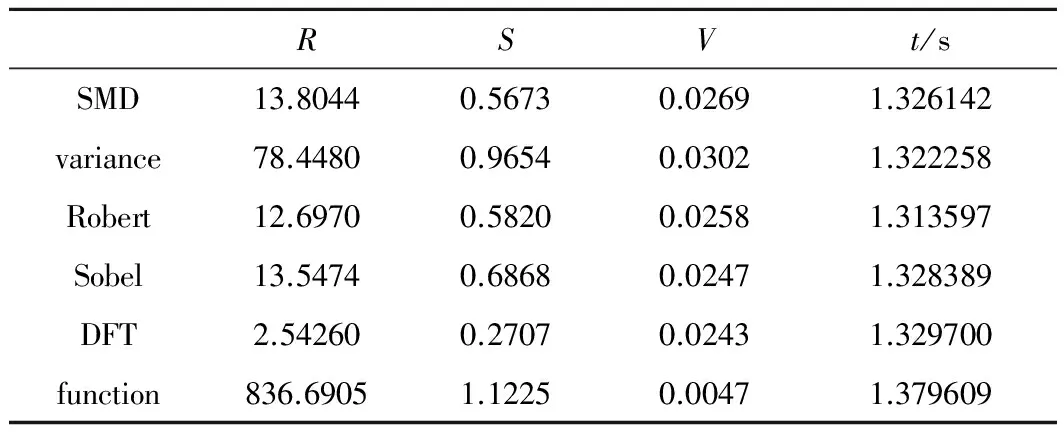
Table 1 Performance index of each focusing function with light intensity of 1.5

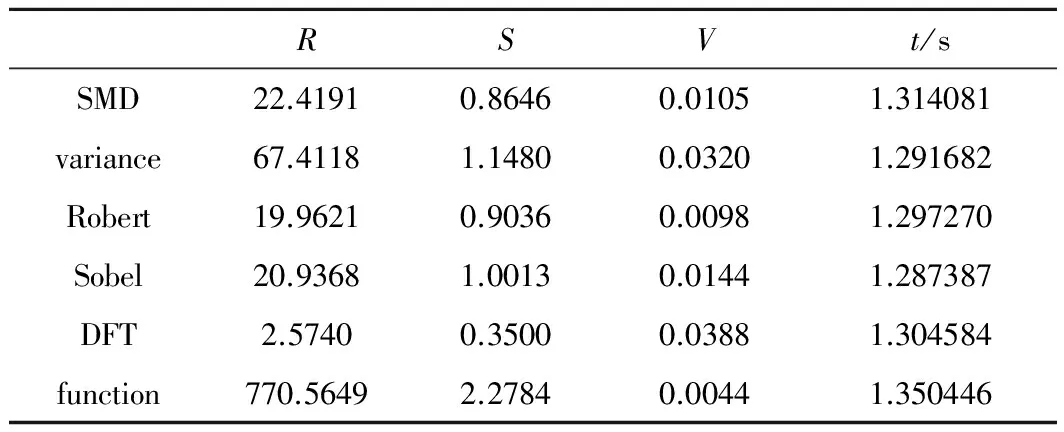
Table 2 Performance index of each focusing function with light intensity of 2

從表1、表2可以看出，在低照度的條件下，本文中聚焦評價函數的清晰度比率遠遠大于傳統的聚焦函數，證明該函數對于不同程度的離焦圖像具有較強的分辨力，同時也說明了本文中函數具有較強的抗噪性。而本文中聚焦評價函數的靈敏度因子提高了0.1571～1.9284，相比傳統的聚焦評價函數，該函數的靈敏度因子至少提高了16.3%，說明該函數具有較高的靈敏度，且在函數最大值附近變化劇烈，適用于精聚焦階段。平緩區波動量的大小，表征一個函數的抗噪性能強弱，而本文中聚焦評價函數的平緩區波動量最小，該函數的平緩區波動量減少了0.0054～0.0344，相比于傳統的聚焦評價函數，該函數的平緩區波動至少減少了55.1%，說明該函數抗噪性強，且具有較強的穩定性。

從時間上來看，本文中函數的耗時和傳統的聚焦函數相差不多。主要是因為本文中函數在計算的過程中有轉換到頻域，一般頻域類函數計算復雜且計算量大，但在驗證的過程中，利用參考文獻[18]中的方法先確定了聚焦窗口，大大減少了計算量，且計算DCT高頻零系數個數只是簡單地對圖像塊計算零系數數目，故在耗時上稍慢于傳統的聚焦函數。

4 結 論

聚焦評價函數是顯微鏡自動聚焦系統的重要環節，通過分析聚焦評價函數的理想曲線特性，本文中提出一種基于頻域DCT零系數和空域局部標準差的自動聚焦算法，該算法在光照強度適宜的條件下，與傳統的聚焦函數均能保持良好的聚焦特性，但在光照強度較弱的情況下，大多數傳統聚焦函數會失去理想的曲線特性，容易造成聚焦的不準確。而本文中函數在低照度的情況下，還能保持良好的曲線特性，且在靈敏度、抗噪性和穩定性方面具有一定的優勢。綜上所述，本文中函數適用于顯微鏡自動聚焦系統。

[1] ZOU Ch F, LIU B Q, HUANG F Y,etal. Automatic focusing evaluation function based on multi-directional maximal gradient threshold method [J]. Laser & Infrared, 2016,46(1):115-118 (in Chinese).

[2] ZHANG L X, SUN H Y, GUO H Ch,etal. Auto focusing algorithm based on largest gray gradient summation[J]. Acta Photonica Sinica, 2013, 42(5):605-610(in Chinese).

[3] LIU P, WANG Ch P, FU Q,etal. Auto-focusing method based on octahedral gradient variance for tracking system [J]. Video Engineering, 2013, 37(9):183-186(in Chinese).

[4] MO Ch H, LIU B, DING L,etal. A gradient threshold auto-focus algorithm [J]. Infrared and Laser Engineering, 2014, 43(1):323-327 (in Chinese).

[5] JIN X, MA W H. Study on image definition evaluation function in auto-focusing process [J]. Optical Instruments, 2012, 34(1):59-64(in Chinese).

[6] HAN R Y, WANG J J, NIE K,etal. Adaptive autofocus technique under different contrast [J]. Acta Photonica Sinica, 2012, 41(2):222-227 (in Chinese).

[7] WANG Q, SONG E M, XU X Y,etal. Auto-focusing function for microscope image based on weighted neighborhood correlation [J]. Optics and Precision Engineering, 2008, 16(1):166-171 (in Chinese).

[8] JIANG T, ZUO F, WANG L G. Achievement of auto-focusing in severe defocused state [J]. Laser Technology, 2015,39(6):794-797 (in Chinese).

[9] JARVIS R. Focus optimization criteria for computer image processing [J]. Microscope, 1976, 24(2):163-180.

[10] CHEN G J, ZHU M F, WANG Y K,etal. Study on definition evaluation function based on image contrast variation [C]//Proceedings of the 2007 China—Ireland International Conference on Information and Communications Technologies. Dublin，Ireland: IET, 2007:254-258.

[11] GAO Z, JIANG W, ZHU K F,etal. Auto-focusing algorithm based on Roberts gradient [J]. Infrared and Laser Engineering, 2006, 35(1): 117-121(in Chinese).

[12] ZHAI Y P, ZHOU D X, LIU Y H,etal. Design of evaluation index for auto-focusing function and optimal function selection [J]. Acta Optica Sinica, 2011, 31(4):0418002(in Chinese).

[13] PENG G J. Video information transmission and processing and application technology development of remote microscopy workstation [D].Guilin:Guilin University of Electronic Technology, 2015:34-35 (in Chinese).

[14] ZHU Q, JIANG W, BEN X Y,etal. Auto-focusing algorithm based on gradient and correlation [J]. Optical Technique, 2016, 42(4):329-332 (in Chinese).

[15] MARICHAL X, MA W Y, ZHANG H J. Blur determination in the compressed domain using DCT information[J]. IEEE Xplore, 2002,2(2):386-390.

[16] XIAN Zh Y, GAN J M, YU Zh M,etal. A method for detecting image defocus blurred region based on correlation and local standard deviation [J]. Computer Applications and Software, 2014,31(9):198-200(in Chinese).

[17] ZHAI Y P, LIU Y H, ZHOU D X,etal. Autofocusing method for microscopy with low image content density [J]. Journal of Software, 2012, 34(5):1281-1294 (in Chinese).

[18] LI H G, WANG Sh, SHA X P,etal. Study of auto focusing technique of micro-vision system [J]. Opto-Electronic Engineering, 2014, 41(8):1-9(in Chinese).

AutomaticfocusingalgorithmbasedonDCTcoefficientofzeroandlocalstandarddeviation

LüMeini1,YUZhenming2

(1.College of Information and Communication, Guilin University of Electronic Technology, Guilin 541004, China; 2.Guangxi Colleges and Universities Key Laboratory of Image Processing and Intelligent Information System, College of Wuzhou, Wuzhou 543002, China)

The design and selection of focusing evaluation function was one of the key problems of automatic focusing microscopes. The illumination change would cause function curve to lose its ideal characteristics. The traditional focusing evaluation function can not overcome this problem. In order to solve the problem, an automatic focusing algorithm combining discrete cosine transform (DCT) coefficient of zero of frequency domain and local standard deviation of spatial domain was proposed. DCT coefficient of zero and local standard deviation of sub-blocks were calculated. Division operation was performed by taking advantage of the opposite effect. And square algorithm was used to increase the clarity ratio of the algorithm. Under different light conditions, compared with several traditional focusing evaluation functions, the focusing experiment was carried out to verify the applicability of the new algorithm. The performance of focus evaluation function was evaluated quantitatively. The results show that the algorithm can keep good curve characteristics under low illumination conditions and has strong anti-noise ability, sensitivity and stability.

image processing; automatic focusing; focusing evaluation function; discrete cosine transform coefficient of zero; local standard deviation

1001-3806(2018)01-0066-06

國家自然科學基金資助項目(61562074)；廣西自治區科學研究與技術開發計劃資助項目(桂科攻1598007-13)

呂美妮(1991-)，女，碩士研究生，主要研究方向為數字圖像處理。

*通訊聯系人。E-mail：yumingming@vip.sina.com

2017-04-10；

2017-04-28

TP391

A

10.7510/jgjs.issn.1001-3806.2018.01.013