解析AISC-89 ASD中K以及Lb對結構強度計算的影響
楊肖龍 李彥麗 安振武 祖 巍
(中海油能源發展裝備技術有限公司 工程設計研發中心 天津300452)
解析AISC-89 ASD中K以及Lb對結構強度計算的影響
楊肖龍 李彥麗 安振武 祖 巍
(中海油能源發展裝備技術有限公司 工程設計研發中心 天津300452)
AISC-89中明確了“ASD”法規定,即在工作載荷作用下,結構構件的應力不應超過規定的容許應力(即“容許應力法”,簡稱“ASD法”)。文中以容許應力法為基礎,對海洋工程鋼結構計算進行深入解讀,歸納總結許用彎曲應力和許用壓應力的計算方法,分析受壓彎構件的有效長度系數K和側向無支撐長度Lb對結構構件強度校核的影響,可供海洋工程鋼結構設計參考。
容許應力法;海洋工程;結構設計;有效長度系數;側向無支撐長度
引 言
作為世界上最具權威的鋼結構設計規范,AISC自1923年問世以來獲得了廣泛應用。至今共推出兩種不同的設計方法,即“容許應力法(ASD)”與“荷載和抗力分項系數設計法(LRFD)”。“ASD法”所基于的概念是:在正常工作載荷作用下結構部件中的最大應力不應超過規定的容許應力[1],容許應力是屈服應力除以安全系數,通過安全系數求得的容許應力的大小取決于起控制作用的特定極限狀態,而安全系數是材料和所考慮構件的函數,僅依賴于傳統經驗。“LRFD法”是以統計方式分析各種荷載使材料破壞的概率,將各種荷載乘以不同的分項系數,作為應力需求,與材料實際的屈服強度比較判斷是否安全。因此,“LRFD法”采用不同的分項系數,可以更精確地模擬不同荷載對結構強度的影響,計算方法更接近于實際,該方法在結構房屋建筑設計方面應用越來越廣泛。
ANSI/AISC 360-10中也給出“ASD法”,但是該方法有別于傳統的AISC-89版“ASD法”,而是將抗力系數和安全系數進行關聯的簡單方法,使“ASD法”與“LRFD法”具有相同的失效控制模式和承載 力 標準 值[2]。API RP 2A-WSD2014認 為 ANSI/AISC360-10版適用于鋼框架房屋建筑設計,而對于海洋平臺而言,其環境相對更加惡劣,基于保守考慮,API不推薦采用“LRFD法”,而是推薦采用AISC-89版“ASD法”[3]。目前,國內海洋平臺的結構設計普遍沿用API RP 2A的推薦做法。國內,羅剛[4]對不同的鋼結構設計方法進行詳細的對比研究。
基于“ASD法”進行結構設計時,許用應力的計算是判斷結構構件是否滿足設計要求的基準,而構件的有效長度系數K和側向無支撐長度Lb對許用應力的計算有直接影響。對于海洋平臺立柱以及斜撐的設計,API RP 2A-WSD 2014已經有明確規定,本文主要探討有效長度系數和側向無支撐長度對受壓I型或H型截面梁結構強度校核的影響。
1 截面類型定義
AISC根據截面尺寸將鋼構件截面劃分為緊湊型(Compact)、非緊湊型(Noncompact)和薄柔型(Slender)三種。該分類方法以構件受壓截面的寬厚比為判斷依據,AISC-89版定義了具體的劃分依據,本文對部分常用構件的分類進行匯總和完善,見表1。

表1 受壓構件截面單元寬厚比類型表
另外,AISC根據約束形式將構件截面分為加筋單元(Stiffened element)和非加筋單元(Unstiffened element)。加筋單元定義為沿力的方向兩端有支撐的單元,例如I型、H型鋼的腹板;非加筋單元定義為沿力的方向一端有支撐的單元,例如I型、H型鋼翼緣的外伸枝、槽鋼的翼緣等[5]。AISC根據構件截面的類型,規定了許用應力的不同計算方式。
2 許用壓應力
2.1 規范分析
有效長度系數K,用于計算受壓構件的許用壓應力,Kl為等效長度,Kl/r稱為長細比,是衡量構件剛度的標志,l為構件實際長度,r為構件截面回轉半徑,單位均為m。對于H型鋼,K值按照截面方向可分為Ky、Kz,本文取一種進行分析。
(1)對于緊湊型和非緊湊型截面,當Kl/r 式中:Fy為構件的屈服強度,MPa;Cc為構件整體屈曲判斷標準,規定: 當Kl/r>Cc時,構件發生整體屈曲的臨界載荷值小于使構件屈服的載荷值,因此以構件屈曲作為結構強度的判斷依據,那么構件許用壓應力為: (2)以上公式是針對緊湊和非緊湊截面,而對于含有薄柔型單元的構件,由于其結構特性需要考慮相應的折減系數。以H型鋼為例,對于薄柔型截面,當時,受壓構件許用壓應力為: 當時,受壓構件許用壓應力為: 式中:b為非加筋受壓單元寬度;t為非加筋單元厚度;Fy為屈服強度;當h/t>70,kc= 4.05/(h/t)0.46;其他情況,kc=1.0。 Qa為 加筋單元折減系數,Qa=Aeffective/Aactual,有效截面積Aeffective計算詳見AISC(89版)附錄B5.2。 從式(1)和式(3)可以看出,對于給定的某種材質的型鋼,其屈服強度和彈性模量是確定的,那么受壓構件的許用壓應力只是長細比Kl/r的分段函數,對于H型鋼,有強軸和弱軸之分,長細比取二者之間的較小值計算許用壓應力。以JIS SM490YB材質的型鋼為例,其屈服強度Fy=345 MPa,彈性模量E=2.06E5 MPa,其許用壓應力隨長細比的變化曲線如圖1所示,Kl/r=Cc為分段函數的臨界值。 圖1 許用壓應力曲線 從圖中可以看出,受壓構件的許用壓應力隨著長細比的增大顯著降低,基于上述原因AISC對長細比給出明確的規定,對于受壓構件長細比不能大于120,受拉構件長細比不能大于300。 有效長度Kl決定了構件許用壓應力,有效長度系數K與構件端部約束有關,更準確地說,當無側向支撐的構件受到足夠大的軸向荷載時,其有效長度取決于其端部抵抗側向位移的能力。顯然,固支約束要強于絞支約束,絞支約束強于自由端,詳見表2。 表2 不用約束方式的構件有效長度系數表 對于海洋工程中常見的平面框架結構,一般設計為縱橫交錯的主梁和次梁,這種結構不同于兩端約束的簡單構件,是一種空間結構體系。在結構計算中,需要考慮次梁是否對主梁的側向變形產生影響。AISC給出門型框架結構立柱有效長度的系數計算經驗公式: 式中:Ic和Lc分別為立柱的慣性矩和長度;Ig和Lg分別為立柱側向支撐構件的慣性矩和長度。通過G值確定有效長度系數K值。G值越大,立柱側向支撐構件對其約束能力越差,有效長度系數越大;反之,G值越小,立柱側向支撐構件對其約束能力越強,有效長度系數越小。 以受壓H440×300×11×18型鋼為例,長度為2.0 m,屈服強度為345 MPa,假設有效長度系數為0.7,計算其許用壓應力。 首先,判斷型鋼翼緣和腹板的截面單元特性,根據表1,受壓I型鋼翼緣判斷公式計算如下: 翼緣:b/t=150/18=8.3,由表1可知臨界值為故判斷翼緣為緊湊單元。 腹板:H/tw= 404/11=36.7,由表 1可知臨界值故判斷腹板為薄柔型單元。 因此Qs=1,而腹板需考慮面積折減,Qa=Aeffective/Aactual=0.99。 根據截面尺寸可得弱側回轉半徑rz=0.072 m,細長比Kl/r=19.5,Cc=106.97。 根據式(4),計算得到許用壓應力Fa=195.6 MPa,根據API規范,結構實際壓應力應與此值對比校核。 采用SACS軟件結構強度分析,在水平層有主次分明的H型鋼框架,對于受壓主梁而言,如果側向的支撐小梁對主梁翼緣的屈曲產生抵抗影響很小,那么需要對主梁的側向無支撐強度進行修正。AISC規定側向無支撐長度Lb作為計算H型鋼強軸方向許用彎曲應力的判斷依據。 首先,根據AISC規范,令 3.1.1 對于H型鋼強軸受彎作用 (1)當Lb≤Lc時 對于緊湊型截面(翼緣板為緊湊型單元,不含Hybird beams和屈服強度高于450 MPa的構件) 困擾云服務行業的另一個問題是數據備份機制,以及存儲在云中的信息究竟如何避免濫用或丟失的問題。這些企業是不能確保數據備份會存儲在單獨的磁帶或者專門的設備上的。事實是,你的這些備份信息會與其他客戶的數據一起存儲在供應商可以負擔得起的備份媒介上。可怕的是,你不會知道誰,何時,能夠訪問這些信息。 對于非緊湊型截面I(翼緣板為非緊湊型單元,腹板為緊湊單元) 對于非緊湊型截面II(翼緣板和腹板均為非緊湊型單元的Built-up members) 式中 :當h/tw>70,kc= 4.05 / (h/tw)0.46,否則kc= 1.0。 對于其他非緊湊型截面 (2)當Lb>Lc時 分為兩種情況,第一種許用彎曲應力以l/rT值為界限進行區分。 第二種對于任意的l/rT: 從式(14)、式(15)和式(16)來看,對于給定結構形式的構件,其許用彎曲應力Fb是側向無支撐長度l的單一函數,其中式(14)、式(15)是以l/rT值為界限的分段函數,式(16)為連續函數,通過這兩種方式計算可以得到兩條不同的函數曲線,許用彎曲應力取二者的較大值。 3.1.2 對于H型鋼弱軸受彎作用 對于緊湊型對稱截面 對于非緊湊型截面 以型鋼H440×300×11×18和H800×300×16×25為例,長度l=2 m,其中H440屈服強度為345 MPa,H800屈服強度為550 MPa。分析在強軸受彎作用下不同側向無支撐長度Lb對許用彎曲應力的影響。 對于H440型鋼,根據式(9)計算得到Lc=3.22 m,以Lc為判斷基準: (1)當Lb≤Lc,即側向無支撐長度取值小于等于3.22 m,根據表1,公式計算H440翼緣為緊湊截面,許用彎曲應力應按照式(10)計算; (2)當Lb>Lc,許用彎曲應力應按照式(14)、式(15)和式(16)計算,取二者中較大值,且不超過0.6Fy。直觀的分析,如圖2所示,對于Lb>Lc的情況,按照式(14)、式(15)和式(16)計算的許用彎曲應力分別為圖2中曲線F(14)、F(15)和曲線F(16),從圖中可以看出按照式(16)計算的許用彎曲應力較大,應以此曲線作為不同Lb值時許用彎曲應力的取值,但不超過0.6Fy。 圖2 H440許用彎曲應力曲線圖 綜上所述,圖中實線(共3段)為許用彎曲應力隨側向無支撐長度Lb而變化的曲線。 對于H800型鋼,根據式(9)計算得到,Lc= 2.35 m,以Lc為判斷基準。 (1)當Lb≤Lc,即側向無支撐長度取值小于等于2.35 m,根據表1公式計算H800翼緣為緊湊截面,許用彎曲應力應按式(10)計算; (2)當Lb>Lc,許用彎曲應力應按式(14)、式(15)和式(16)計算,取二者中較大值,且不超過0.6Fy。直觀地分析(如圖3所示),采用上述公式計算的許用彎曲應力有多個交叉點,所以H800型鋼許用彎曲應力分為多段曲線。按式(14)、式(15)計算的許用彎曲應力分別為曲線F(14)和F(15),P2為分界點;按式(16)計算的許用彎曲應力為曲線F(16),其中曲線F(16c)代表的應力值大于式(14)、式(15)計算的應力值(P1和P3為分界點),但不超過0.6Fy。 圖3 H800許用彎曲應力曲線圖 綜上所述,圖3實線(共6段)為H800型鋼許用彎曲應力隨側向無支撐長度Lb而變化的曲線。 本文以AISC-89版為基礎,對海洋工程鋼結構校核進行深入研究,重點分析鋼結構許用壓應力和許用彎曲應力計算的影響因素,總結為以下幾點: (1)總結鋼結構截面類型的分類和判斷標準,以及截面類型的劃分是結構許用應力計算的首要要素。 (2)根據理論計算分析受壓構件有效長度系數K對結構許用壓應力的影響,對于給定材質、截面類型的構件,其許用壓應力只與構件的長細比有關。 (3)根據理論計算分析受彎構件的側向無支撐長度Lb對結構許用彎曲應力的影響,對于給定材質、截面類型的構件,其許用彎曲應力只與側向無支撐長度Lb有關,但判斷條件較為復雜,表現為多區間函數。 綜上所述,有效長度系數K和側向無支撐長度Lb對許用彎曲應力的計算具有較大影響,海洋工程設計可根據結構特點并結合上述研究分析對有效長度系數K和側向無支撐長度Lb進行合理地修正,以保證結構設計的可靠性與安全性。 [1] AISC. Manual of Steel Construction-Allowable Stress Design[S]. American Institute of Steel Construction,Inc,1989. [2] ANSI/AISC 360-10,Specification for Structural Steel Buildings[S]. American Institute of Steel Construction,Inc,2010. [3] API RP 2A,Planning, Designing, and Constructing Fixed Offshore Platforms-WSD[S]. American Petroleum Institute,2014. [4] 羅剛.中美鋼結構基本構件安全度差異的比較分析[J].浙江建筑,2010(12):12-16. [5] 張慶芳,張志國.中外鋼結構規范腹板有效寬度確定方法對比[J].鋼結構,2008(5):45-48. [6] 王雪飛,王鐵紅,孫新.解讀美標(AISC-ASD89)鋼結構構件強度的計算方法[J].吉林建筑工程學院學報,2010(3):4-8. Influence of K and Lbon structural strength calculation based on AISC-89 ASD YANG Xiao-long LI Yan-li AN Zhen-wu ZU Wei In the AISC-89 ASD, the stress of the structural members under the working load should not exceed the allowable stress, which is called as allowable stress design and plastic design(ASD) method. The calculation of offshore engineering steel structure is then thoroughly interpreted based on the ASD method. The article summarizes the calculation methods of allowable bending stress, allowable compression stress, and analyzes the influence of the effective length factor K and the laterally unsupported length Lbof the compressed members on the structural strength calculation. It can provide reference for the design of offshore engineering steel structure. allowable stress design and plastic design(ASD); offshore engineering; structural design; effective length factor; laterally unsupported length U661.43 A 1001-9855(2017)06-0037-06 10.19423 / j.cnki.31-1561 / u.2017.06.037 2017-05-23; 2017-06-23 楊肖龍(1985-),男,碩士,工程師。研究方向:海洋工程結構設計。 李彥麗(1982-),女,碩士,工程師。研究方向:海洋工程結構設計。 安振武(1981-),男,碩士,工程師。研究方向:海洋工程結構設計。 祖 巍(1987-),男,工程師。研究方向:海洋工程結構設計。


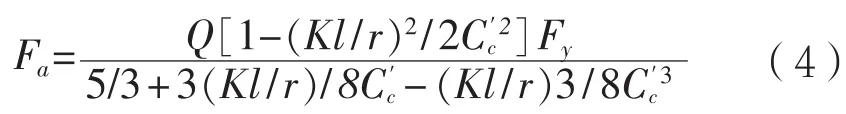

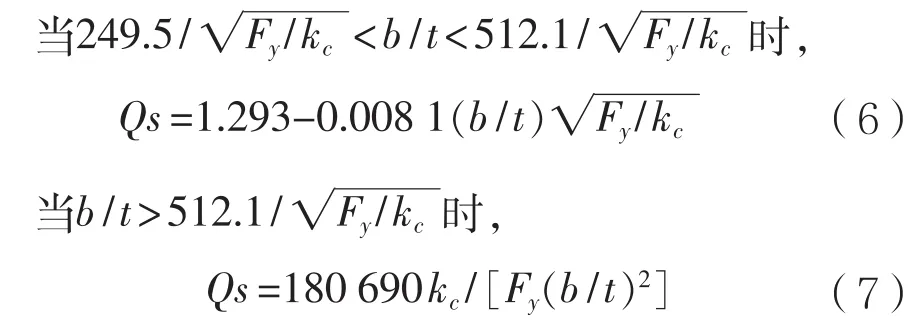

2.2 K值選取


2.3 算 例
3 許用彎曲應力
3.1 規范分析









3.2 算 例

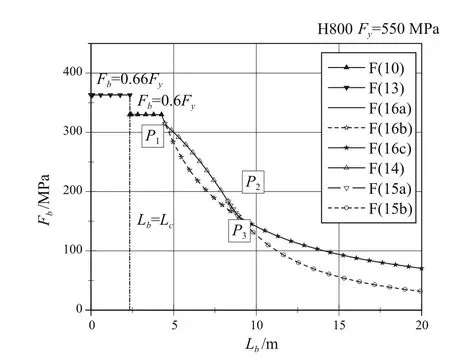
4 結 論
(CNOOC Ener Tech Equipment Technology Research & Design Center,Tianjin 300452, China)

