探究一道高考題幾何背景的心路歷程

江西省萍鄉中學 (337000)

黃賢鋒

探究一道高考題幾何背景的心路歷程

江西省萍鄉中學 (337000)

黃賢鋒

眾所周知，解析幾何首先是幾何.“代數”只是我們解決幾何問題時用到的工具，學生在解答過程中，首先要將幾何圖形的性質用代數的語言來描述，最終是通過坐標的代數運算來研究幾何圖形的性質，“幾何”是我們思考的起點和終點，也是問題的緣起和歸宿.歷年高考中的圓錐曲線解答題除考查解析幾何基本思想之外，均富有深刻的幾何內涵，下面就2017年高考全國Ⅱ卷第20題為例，談談對其幾何本質的探究過程.

(Ⅰ)求點P的軌跡方程；

試題考查了動點軌跡問題、直線在運動變化過程中過定點的問題，結論的“幾何味”頗濃，而題設條件卻是“向量的數乘、數量積”等代數關系式，這些數量關系是如何影響或決定圖形中的點、線位置關系的呢？該試題的幾何本質特征是什么呢？筆者帶著這些問題開啟了探究之路.

一、轉化條件，揭示幾何特征

圖1

圖2

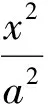
類似地，在雙曲線中也有如下結論.

圖3

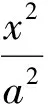
(證明過程從略)

二、弱化條件，探究幾何規律

當筆者想把結論推廣到拋物線中時，似乎遇到了障礙，反思上述結論，突然發現條件和結論之間僅僅是數量關系之間的內在聯系，和曲線的形狀好像無關，于是，決定淡化圓錐曲線這個“背景”，探究更一般的規律，于是得到：

探究至此，深感這道高考試題的綜合性之強，幾何背景之深厚，試題的本質最終回歸到平面幾何中的重要定理——圓冪定理，凸顯了平面幾何與解析幾何之間的交融.