一道2017年高考向量試題的多角度探究及啟示

安徽省滁州中學 (239000)

程潤申 王 圣

一道2017年高考向量試題的多角度探究及啟示

安徽省滁州中學 (239000)

程潤申 王 圣

1.真題再現

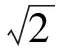
上述試題是2017年全國新課標卷Ⅲ理科選擇題第12題，主要考察了平面向量的坐標運算，平面向量基本定理，應用平面向量基本定理表示向量的實質以及利用平行四邊形法則或三角形法則進行向量的加、減或數乘運算.考查內容豐富，綜合性較強.本文擬從不同的角度對此題作多角度的探究.

2.探究過程

2.1 探究角度一：通過“自乘”的方法，把向量關系轉化為數量關系，進而求解λ+μ的最大值

下面通過不同路徑研究λ+μ的最大值：

圖1

2.2 探究角度二：通過“它乘”的方法，把向量關系轉化為數量關系，進而求解λ+μ的最大值

下面解法同法一.

2.3 探究角度三：通過向量系數分解回歸向量概念本質，進而求解λ+μ的最大值

由平行四邊形法則分解如圖2所示，在ΔPNC中由正弦定理可得

圖2 圖3

2.4 探究角度四：通過建立平面直角坐標系，把向量問題代數化，進而求解λ+μ的最大值.

2.5 探究角度五：挖掘向量背后的平面幾何意義，進而求解λ+μ的最大值

3.探究過程的一點啟示

向量本身既有大小，又有方向，向量相關知識融合數形于一體，能夠較好的綜合考查代數，幾何，三角，不等式等各個章節的內容，使得他們有機的聯系到一起.在具體解決問題過程中，向量本身就成為了一個重要的工具，與平面向量相關的最值問題，頻率較高的出現在各地的模擬試卷以及高考試卷中，經久不衰.也是高中學生學習的一個難點.

3.1 抓住向量概念中的代數特征，以數輔形

向量問題解決的本質在于概念本身的理解，有長度方向，兩者需兼顧不可荒廢，但在具體的問題中，顯現出的外在表征不同，促使我們同學在解決問題的過程中有所傾向.抓住問題本質，建立坐標也不失為是解決向量問題的一個很好代數手段，同時，函數方程觀點，向量三角不等式，三角工具，數量積公式，極化恒等式等等都是可以作為輔助工具使用，也能較好的考查學生的基本運算能力.

3.2 抓住向量知識中的幾何特征，以形助數

向量的方向性決定了向量問題中的幾何特征，但在具體的應用過程中，包括我們的教師在高三復習的很多時候都強調能建立坐標系的盡量建坐標，這樣能減少“思維量”，這里所謂的“思維量”恐怕就是我們經常所說的平面向量背后所具有的幾何屬性.涉及到平面幾何相關性質，我們的學生在解決問題的過程中確實有所“怵”，但這樣的“怵”是不是和我們或多或少的教學暗示或者走捷徑有關，可以讓學生去探究提煉相關幾何背景，比如投影的幾何意義，線圓等相關初中幾何知識和性質的總結和應用.在潤物細無聲中慢慢滲透向量的幾何特征，以幾何屬性提升化簡運算的能力.

對于向量的復習，我們不需要題海戰術，可以以經典高考向量試題，通過不同角度的激發學生合作探究，直至最終解決問題來構建高三向量復習微專題，在數中顯形，在形中助數.