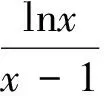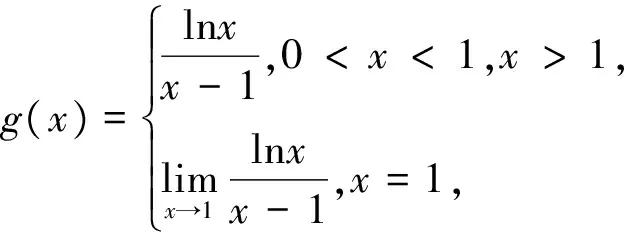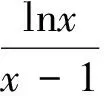2015-2017年高考數學全國卷導數命題的幾個視角*
2018-01-03 01:41:53四川內江師范學院數學與信息科學學院641100
中學數學研究(江西) 2017年12期
四川內江師范學院數學與信息科學學院 (641100)
董萬平 余小芬 袁小燕
2015-2017年高考數學全國卷導數命題的幾個視角*
四川內江師范學院數學與信息科學學院 (641100)
董萬平 余小芬 袁小燕
導數是微積分的初步知識，也是微分學的重要內容，同時還是刻畫函數和曲線性態的有力工具.近年高考中，導數考點深受命題者青睞，題型覆蓋客觀題和解答題，內容上體現了與函數、三角函數、數列、向量、不等式、概率等知識的交匯融合，蘊含了數形結合、分類與整合、化歸與轉化、函數與方程等基本數學思想方法.充分考查學生的抽象思維能力，邏輯推理能力，運算求解能力.本文以近三年高考數學全國卷中導數試題為例，分析導數考查的幾個視角.
視角一 利用導數的定義求極限
例1 (2017年全國卷Ⅱ，文21)函數f(x)=(1-x2)ex.
(Ⅰ)討論f(x)的單調性；
(Ⅱ)當x≥0時，f(x)≤ax+1，求a的取值范圍.
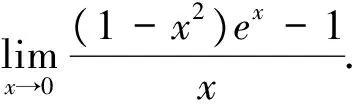
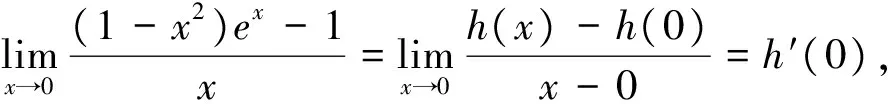
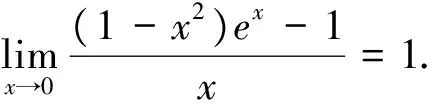
視角二 利用導數的幾何意義求解曲線的切線問題
導數的幾何意義體現了導數與曲線的聯系，蘊含著“以直代曲”的重要數學思想.利用導數的幾何意義求解曲線的切線問題是導數的一種最基本應用.該類問題主要考查學生對導數幾何意義的理解及求導公式、求導法則的應用，高考中常以選擇、填空題形式出現，有時也滲透在解答題中，難度中等.
例2 (2015年全國卷I，文14)已知函數f(x)=ax3+x+1的圖像在點(1,f(1))處的切線過點(2,7)，則a=________.
解:f′(x)=3ax2+1，則f(x)在點(1,f(1))的切線斜率為k=f′(1)=3a+1，又f(1)=a+2，故切線方程為y-(a+2)=(3a+1)(x-1)，代入(2,7)，解得a=1.
點評:利用導數的幾何意義求解曲線的切線問題時，一定要把握“切點坐標”這一關鍵要素.同時要注意“在某點處的切線”與“過某點的切線”的區別，進而才能準確表達切線斜率.近三年全國卷類似考題還有：2017年全國卷Ⅰ文科14題，2016年全國卷Ⅲ文科16題、理科15題，2016年全國卷Ⅱ理科16題，2015年全國卷I理科12題，2015年全國卷Ⅱ文科16題.
視角三 利用導數研究函數的單調性、極值與最值
導數是研究函數單調性、求解極值與最值、刻畫函數圖像變化趨勢的重要工具.近年高考中以此為背景的試題屢見不鮮.
例3 (2017年全國卷Ⅱ，理11)若x=-2是函數f(x)=(x2+ax-1)ex-1的極值點，則f(x)的極小值為( ).
A.-1B.-2e-3C.5e-3D.1
解:f′(x)=ex-1[x2+(2+a)x+a-1].由x=-2為f(x)的極值點得f′(-2)=0，解得a=-1.故f′(x)=ex-1(x2+x-2)，令f′(x)=0，解得x1=-2或x2=1.容易分析f(x)的極小值為f(1)=-1.故選A.
點評:本題考查求解可導函數極值的一般步驟，難度中等，重點強調對極值概念的理解及求導公式、法則的正確使用.理解極值概念時，應把握極值反映的是函數的局部最值特征.函數在點x0處取得的極值未必是函數的最值，要區分極值與最值的“局部”與“整體”關系.其次，對可導函數f(x)而言，f′(x0)=0只是f(x)在點x0處取極值的必要條件，而非充要條件.
例4 (2015年全國卷Ⅱ，文21)已知f(x)=lnx+a(1-x).
(Ⅰ)討論f(x)的單調性；
(Ⅱ)當f(x)有最大值,且最大值大于2a-2時,求a的取值范圍.
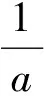
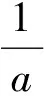
令g(a)=lna+a-1，則g(a)在(0,+∞)是增函數，且g(1)=0.于是當0
視角四 利用導數研究函數的零點問題
利用導數求解函數零點、估算零點范圍，判斷零點個數以及已知函數零點求參數范圍，是導數綜合運用的體現，也是近年高考的熱點問題.該類問題常涉及對函數零點、方程根、兩函數圖像交點的橫坐標之間關系的理解，以及對零點存在性定理的靈活應用，滲透著分類討論、化歸與轉化、數形結合等基本思想.
例5 (2017年全國卷Ⅰ，理21)已知函數f(x)=ae2x+(a-2)ex-x.
(Ⅰ)討論f(x)的單調性；
(Ⅱ)若f(x)有兩個零點，求a的取值范圍.
解:(Ⅰ)f(x)的定義域為(-∞,+∞).當a≤0，f(x)在(-∞,+∞)單調遞減.當a>0，f(x)在(-∞,-lna)單調遞減，在(-lna,+∞)單調遞增.
點評:本題考查利用導數求解函數的單調性、最值及零點的綜合問題，考查學生對問題的分析、轉化及運算能力.(Ⅱ)利用(Ⅰ)問單調性結論作為零點問題分類討論的依據，并結合零點存在性定理將函數零點問題轉化為函數最值與0的大小問題，進而求解a的范圍.問題的解決中對不等式放縮技巧要求較高.當然解決(Ⅱ)問還可利用分離參數法，或轉化為兩函數圖像的交點問題進行處理，考生可根據知識把握情況，靈活選取.近三年全國卷類似考題還有：2017年全國卷Ⅲ文科12題、2016年全國卷Ⅰ理科21題.
視角五 利用導數證明不等式
不等式的證明問題是高中數學的難點，解決問題所涉及的方法多樣，技巧性靈活，學生不易把握.通過導數研究函數的單調性，再由單調性證明不等式，這種解決問題的思路清晰，操作性強，易于掌握，同時也體現了函數與導數、不等式的綜合應用.
例6 (2017年全國卷Ⅲ，理21)已知函數f(x)=x-1-alnx.
(Ⅰ)若f(x)≥0，求a的值
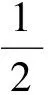
解:(Ⅰ)f(x)的定義域為(0,+∞).
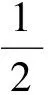
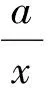
(Ⅱ)由(Ⅰ)問，當x∈(1,+∞)時，x-1-lnx>0，即lnx 點評:本題是一個有遞進關系的綜合問題，通過導數解決(Ⅰ)問中不等式的恒成立問題，求得a值，進而獲得解決(Ⅱ)問的“隱性條件”lnx 利用導數研究函數存在性問題或恒成立問題是歷年高考考查的難點、熱點.主要考查導數與函數、方程、不等式的綜合應用. 例7 (2017年全國卷Ⅱ理科，21)已知函數f(x)=ax2-ax-xlnx，且f(x)≥0. (Ⅰ)求a. (Ⅱ)證明：存在唯一的極大值點x0，且e-2 解:(Ⅰ)f(x)的定義域為(0,+∞).f(x)≥0等價于a(x-1)≥lnx. 綜上，對任意x∈(0,+∞)，f(x)≥0成立，則a=1. (Ⅱ)由(Ⅰ)知f(x)=x2-x-xlnx，f′(x)=2x-2-lnx. 當然，導數的考查視角絕不止上述總結，限于篇幅，本文僅以全國卷試題為例，權作拋磚引玉，有興趣的讀者可結合地方省份高考試題作進一步研究，比如利用導數解決函數圖像交點問題、處理極值偏移點問題等. 四川省"西部卓越中學數學教師協同培養計劃"項目(ZY16001).余小芬系本文通訊作者.
視角六 利用導數研究存在性、恒成立問題
