一道例題的多視角探究

江蘇省蘇州工業園區第二高級中學 (215121)

南愛玲

一道例題的多視角探究

江蘇省蘇州工業園區第二高級中學 (215121)

南愛玲

著名數學家波利亞在其著作《怎樣解題》中給出一張解題表，包括弄清問題，擬定計劃，實現計劃，回顧.弄清問題就是我們通常說的審題，分析理解題目中的條件，研究問題的結論；擬定解題方案，這一過程中要有理性思維，分析解決問題需要的條件，如何實現與已知條件之間的轉化；實現計劃，就是具體解決問題的過程，在解題過程中不斷調整策略；回顧，就是解題后進行總結和反思，完善解題認知結構.而解題教學時數學課堂的一個重要組成部分，教師不僅要教會學生怎樣解題，還應該探究數學思維的過程，解題后養成回頭看一看的習慣，也就是我們通常所說的解題反思，反思解決問題的方法和思路.本文遵循波利亞的解題步驟，從不同的視角對一道典型例題進行探究.

一、弄清問題，高屋建瓴

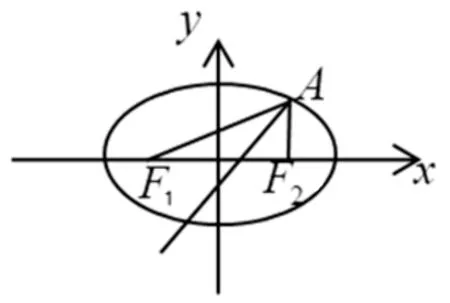
圖1

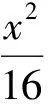
審題是解題的首要環節，深入細致的審題是順利解題的前提，因此在平時的解題教學中，要引導學生重視審題.

審題就是要弄清楚題目的背景，分析題目中的已知條件，弄清要解決的問題.這是一道求直線方程的問題，直線的方程在江蘇省考試說明中是C級要求內容，要求系統地掌握知識的內在聯系，并能解決綜合性較強或較為困難的問題.本題以橢圓為背景，給定橢圓上一定點A(2,3)，求兩個焦點F1,F2對點A張角的平分線，從難易程度上來講，屬于基礎題，但是判斷一道題好不好，難易不是唯一的標準，還要看這道題是否典型，是否包含了重要的基礎知識，解題過程中是否能夠多角度探究，培養學生的思維能力，從這個角度看，本題很典型.因為題目中橢圓的方程已知，可以求出橢圓兩焦點F1,F2的坐標，而這個角平分線所在直線必經過點A，那么要求該直線的方程，只要再求出直線上一點坐標或者求出該直線的斜率即可.

二、擬定計劃，深謀遠慮

擬定計劃也就是根據題目中的條件探究解題思路的過程.求直線的方程這種題型對學生來講是一類常見題型，在讀完題目后學生的思路應該就出來了，兩類思路：只要再求出直線的另一點的坐標或者求出直線的斜率.第一種思路中要考慮的問題是求哪一點的坐標呢？我們可以考慮該直線與x軸或者y軸的交點，當然也可以任意取一點P(異于點A)，根據角平分線的性質：角平分線上的點到角的兩邊距離相等，即可求出點的坐標，問題也就隨之解決.而第二種思路中求直線的斜率，相對來講思維難度要大一點.那么這時候要考慮的問題就是求斜率的方法有哪些呢？本題中哪些方法可行？順著這個思路尋求問題的解決辦法.這是一道比較簡單的求直線問題，在實際教學中，有的老師處理這個問題時可能一帶而過，那就很遺憾了，沒有從各個視角深入探究這個問題，也就錯失了利用這道題拓展學生的視野，培養學生分析問題解決問題的能力.

三、實施計劃，靈活應變

(一)求點

(1)特殊點的視角

在求點時往往選擇直線與坐標軸的交點，原因是坐標軸上的點有一個坐標為0，可以簡化運算.這其實也是特殊化的具體應用，特殊化是數學解題教學中尤其是解析幾何中應用較為廣泛，通過對某種特殊位置的考察，來探究一般情況的性質.

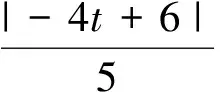
(2)直線方程的定義視角

所謂求直線的方程，其本質就是求直線上任意一點P(x,y)的縱坐標y與橫坐標x之間滿足的關系.如果從這個角度考慮，我們就可以根據角平分線的性質直接求出直線的方程.

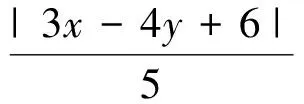
(3)角平分線定理的視角

除了角平分線的性質，我們還可以從角平分線定理的角度來求點.根據角平分線定理，可以求出直線l與x的交點坐標，從而求出直線l的方程.

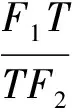
(4)三角形的視角

從三角形的角度來考察本題，由角平分線聯想到等腰三角形中三線合一的性質，此題也迎刃而解.

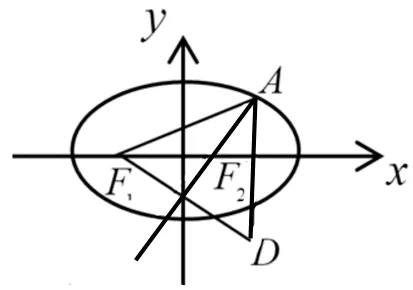
圖2

構建等腰三角形，如圖2，延長AF2至AD使AD=AF1=5，則知點D(2,-2)，由等腰三角線三線合一知F1D的中點M(0,-1)在直線l上，進而求出直線方程.解決問題的過程中用聯系的觀點看問題，這是數學思維必備能力之一.

(二)求斜率

(1)向量的視角

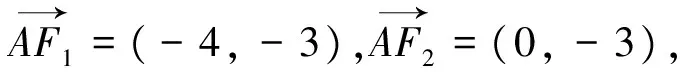
(2)三角函數的視角

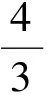
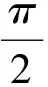
(3)橢圓切線的視角

本題以橢圓為背景，而橢圓的幾何光學性質等也為解題提供了不一樣的視角.

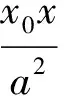
四、反思總結，融會貫通

反思是一種積極的探究行為，通過反思，有利于提高發現問題的能力，有利于完善解題過程，增強自我調控意識.反思解題的過程，運用的數學知識和數學思想方法，反思解題策略，在反思的過程中，加深對問題本質的理解，提煉對數學問題的認識.本題是一道基礎題，學生很容易想到第一種求點的方法，如果問題到這一步就結束，可以說是輕描淡寫的收場，那么師生就會錯過多視角多方位的對這個問題的理解和探究.求點的坐標，那么求哪些點的坐標呢？有哪些不同的方法呢？如果在平時的解題中不僅僅滿足于把問題解決了，而是習慣性地追問自己：還有不一樣的方法嗎？還有更好的方法嗎？如果經常這樣追問自己，解題的方法和思路就會越來越寬，解題能力也會不斷提高.本題是典型的求直線方程問題，除了求點，很自然就會想到，求斜率行不行呢？怎么去求斜率呢？這樣思路就打開了.問題與問題之間不是孤立的，許多表面上看似無關的問題卻有著內在的聯系，解題不能就題論題，要尋找問題與問題之間本質的聯系，要質疑為什么有這樣的問題？他和哪些問題有聯系？能否受這個問題的啟發.將一些重要的數學思想、數學方法進行有效的整合，創造性地設問，在不斷的知識聯系和知識整合中，豐富認知結構中的內容，體驗“創造”帶來的樂趣.

在平時的解題教學中，要有意識的引導學生進行解題回顧和總結，完善解題認知結構.在解題后，引導學生對解題中用到的數學知識點，數學思想方法和解題技巧進行回顧，對典型的問題進行深入地挖掘、研究、引申和推廣，使學生在回顧反思的過程中親身體驗，總結和積累數學解題經驗，從而提升學生的數學解題能力和數學思維能力.