遺傳算法優(yōu)化Prony電力系統(tǒng)諧波檢測(cè)的研究

葛江紅 張昌麗

（1. 國網(wǎng)滁州供電公司，安徽 滁州 239000；2. 國網(wǎng)蕪湖供電公司，安徽 蕪湖 241000）

遺傳算法優(yōu)化Prony電力系統(tǒng)諧波檢測(cè)的研究

葛江紅1張昌麗2

（1. 國網(wǎng)滁州供電公司，安徽 滁州 239000；2. 國網(wǎng)蕪湖供電公司，安徽 蕪湖 241000）

實(shí)現(xiàn)對(duì)電力系統(tǒng)所含諧波的快速、準(zhǔn)確檢測(cè)是對(duì)其進(jìn)行有效抑制、以提高電能質(zhì)量和增強(qiáng)電網(wǎng)穩(wěn)定性的關(guān)鍵技術(shù)。本文通過對(duì)現(xiàn)有電力系統(tǒng)諧波檢測(cè)方法的比較，通過分析含噪聲條件下傳統(tǒng)Prony算法的相關(guān)參數(shù)優(yōu)化選擇方面存在的局限性，并根據(jù)Prony算法可以直接提取待檢測(cè)信號(hào)的相關(guān)參數(shù)的特征，同時(shí)具有較強(qiáng)的自適應(yīng)能力等特點(diǎn)，提出了遺傳算法優(yōu)化 Prony電力系統(tǒng)諧波檢測(cè)方法，以實(shí)現(xiàn)對(duì) Prony方法檢測(cè)諧波相關(guān)參數(shù)的優(yōu)化求取。通過仿真實(shí)驗(yàn)表明，本文所提出的方法對(duì)于不同信噪比條件下的諧波檢測(cè)信號(hào)在擬合誤差精確度以及穩(wěn)定性等方面均具有顯著的優(yōu)勢(shì)。

諧波檢測(cè)；遺傳算法；Prony算法

隨著電力電子技術(shù)的快速應(yīng)用以及非線性負(fù)荷需求的不斷增加，由此所導(dǎo)致的電力系統(tǒng)諧波對(duì)電能質(zhì)量造成了嚴(yán)重的影響。近年來，諧波等相關(guān)原因所造成的大面積停電事故時(shí)有發(fā)生，這不僅對(duì)人民群眾的正常生產(chǎn)生活帶來了極大的不便，而且對(duì)國民經(jīng)濟(jì)的發(fā)展造成了巨大的損失。在此背景下，為了減小甚至避免電力系統(tǒng)諧波對(duì)于電網(wǎng)正常運(yùn)行的不利影響，準(zhǔn)確而有效地對(duì)電力系統(tǒng)諧波進(jìn)行檢測(cè)并適時(shí)采取相應(yīng)的抑制措施，已成為電力系統(tǒng)安全穩(wěn)定運(yùn)行的一項(xiàng)決定性要素[1-2]。

目前對(duì)于電力系統(tǒng)諧波檢測(cè)方面的方法主要有：模擬濾波器諧波檢測(cè)方法、希爾伯特-黃變換檢測(cè)方法、基于神經(jīng)網(wǎng)絡(luò)的檢測(cè)方法、基于傅里葉變換的檢測(cè)方法、基于小波變換的檢測(cè)方法、基于Prony算法的諧波檢測(cè)方法等[3]。其中模擬濾波器檢測(cè)方法硬件電路設(shè)計(jì)簡單，易于實(shí)現(xiàn)，然而其中心頻率帶有參數(shù)敏感性，在實(shí)際中難以獲得滿意的特性參數(shù)，從而使得檢測(cè)結(jié)果存在較大的誤差。希爾伯特-黃變換檢測(cè)方法對(duì)于非線性非平穩(wěn)信號(hào)具有較強(qiáng)的適用性，具有計(jì)算量小的優(yōu)勢(shì)，然而其在諧波檢測(cè)過程中易出現(xiàn)模態(tài)混疊等問題，導(dǎo)致對(duì)于多成分信號(hào)分解穩(wěn)定性較差。基于神經(jīng)網(wǎng)絡(luò)的檢測(cè)方法對(duì)于訓(xùn)練樣本具有較高的依賴性，同時(shí)缺乏標(biāo)準(zhǔn)化的神經(jīng)網(wǎng)絡(luò)模型構(gòu)造方法與流程[4]。基于傅里葉變換的檢測(cè)方法計(jì)算量較大，計(jì)算效率不高，此外當(dāng)待檢測(cè)信號(hào)的頻率與采樣頻率不相匹配時(shí)，易產(chǎn)生頻譜泄露效應(yīng)（柵欄效應(yīng)），從而造成較大的檢測(cè)誤差。作為一種信號(hào)時(shí)域分析中所廣泛采用的工具，應(yīng)用小波變換檢測(cè)并分析電力系統(tǒng)諧波信號(hào)具有較強(qiáng)的普遍性，其可對(duì)待檢測(cè)信號(hào)中的奇異值進(jìn)行準(zhǔn)確定位進(jìn)而判斷其相應(yīng)的干擾類型。然而在實(shí)際檢測(cè)過程中，如何選擇合適的小波基函數(shù)對(duì)信號(hào)進(jìn)行分離目前尚無統(tǒng)一化的指導(dǎo)原則，此外小波變換無法準(zhǔn)確檢測(cè)諧波信號(hào)的頻率與對(duì)應(yīng)的幅值[5]。這些因素都限制了上述方法的廣泛應(yīng)用。

擴(kuò)展 Prony算法模型可以直接提取待檢測(cè)信號(hào)的幅值、頻率、初相以及衰減因子，具有較強(qiáng)的自適應(yīng)能力，無需對(duì)特征方程進(jìn)行求解，也不必進(jìn)行樣本自相關(guān)的估計(jì)驗(yàn)算，僅借助于對(duì)多項(xiàng)式與線性方程組的求解便可得到精確度高的模態(tài)信號(hào)[6-7]。然而，模型參數(shù)的選擇制約著 Prony算法信號(hào)檢測(cè)的最終結(jié)果，在含噪聲條件下這一問題將變得越發(fā)突出。基于此，本文提出利用擴(kuò)展的Prony 算法進(jìn)行電力系統(tǒng)諧波檢測(cè)過程，以啟發(fā)式的智能優(yōu)化算法-遺傳算法對(duì) Prony的相關(guān)參數(shù)（包括幅值、相位、頻率以及衰減因子）進(jìn)行在線優(yōu)化選擇，克服離線模型參數(shù)選擇對(duì)諧波檢測(cè)結(jié)果的不利影響，從而最終實(shí)現(xiàn)提升 Prony算法諧波檢測(cè)精度，減少系統(tǒng)誤差的目的。本文對(duì)含有不同噪聲強(qiáng)度的諧波信號(hào)進(jìn)行了基于Matlab平臺(tái)的仿真實(shí)驗(yàn)研究，結(jié)果顯示該方法相比于傳統(tǒng)的 Prony算法準(zhǔn)確度有了顯著的提升。

1 擴(kuò)展Prony算法理論分析

1795年由法國數(shù)學(xué)家Gaspard Riche和Baron de Prony聯(lián)合提出了Prony算法。該方法最初應(yīng)用于氣體膨脹問題的研究，其基本機(jī)理為通過一系列的指數(shù)函數(shù)的線性組合對(duì)待測(cè)信號(hào)進(jìn)行擬合，以獲取待測(cè)信號(hào)的幅值、相位、頻率以及衰減因子，其數(shù)學(xué)表達(dá)式定義如下：

式中，Ai為幅值；αi為衰減因子；iφ為相角；fi為余弦信號(hào)的頻率，P為阻尼余弦分量的個(gè)數(shù)。

對(duì)于離散時(shí)間諧波檢測(cè)信號(hào) x(n)=[x(0), x(1), …, x(N-1)]，0≤n≤N-1，利用 Prony 方法對(duì)上述信號(hào)進(jìn)行擬合的數(shù)學(xué)表達(dá)式為

式中，采樣間隔為Δt。

假設(shè)式（2）中有衰減直流分量 p1個(gè)，衰減余弦分量p2個(gè)，利用歐拉公式將對(duì)應(yīng)的余弦分量展開表示，同時(shí)令p=p1+p2，則離散時(shí)間表示的待檢測(cè)諧波信號(hào)的函數(shù)形式為

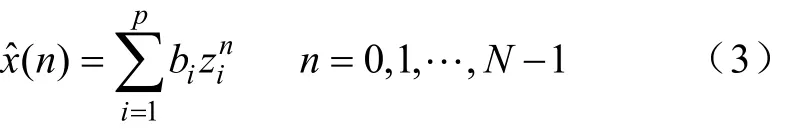
式中，k為模型的階數(shù)；N為采樣點(diǎn)的個(gè)數(shù)，且N≥2n，?()x n為x(n)的擬合估計(jì)值；bi和zi為對(duì)應(yīng)的復(fù)數(shù)。為了實(shí)現(xiàn)信號(hào)估計(jì)值與待檢測(cè)信號(hào)值的精確匹配，利用平方誤差最小的原則，求得上式中的相關(guān)參數(shù)解，使得估計(jì)值與真實(shí)值之間的平方誤差最小。Prony算法認(rèn)為式（2）中的信號(hào)擬合過程是一個(gè)常系數(shù)線性差分方程的齊次解。為此定義多項(xiàng)式：

對(duì)式（2）兩邊同時(shí)乘以ak，再對(duì)p+1個(gè)乘積求和，整理得

定義 e(n)為真實(shí)待檢測(cè)信號(hào) x(n)與其估計(jì)值?()x n之間的誤差，則有

根據(jù)上式有

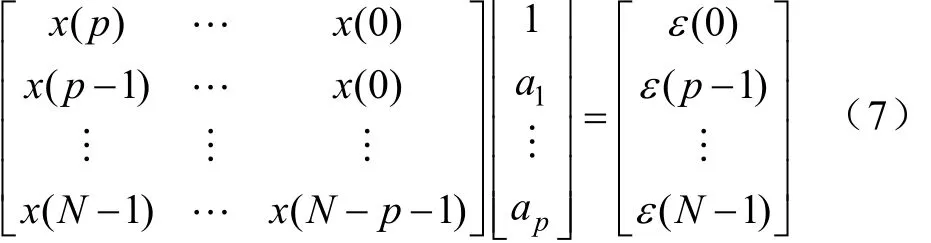
擴(kuò)展 Prony算法即是求解上述方程的線性最小二乘解。根據(jù)式（7）中的參數(shù) a1, a2,…, ap可求得特征方程式1+a1z-1+…+apz-p=0的根，即為Prony的極點(diǎn)。根據(jù)zk的取值，式（2）即可化簡為線性方程，其相應(yīng)的矩陣形式表示如下：

由上述推導(dǎo)過程可知，擴(kuò)展 Prony算法的實(shí)質(zhì)是將非線性求解問題轉(zhuǎn)換為線性差分問題進(jìn)行求解，通過最小二乘法實(shí)現(xiàn)曲線擬合過程，以對(duì)信號(hào)中的各個(gè)參數(shù)值進(jìn)行計(jì)算。

2 遺傳算法優(yōu)化Prony的諧波檢測(cè)

2.1 遺傳算法原理

遺傳算法（Genetic Algorithm）是模擬達(dá)爾文生物進(jìn)化論的自然選擇和遺傳學(xué)機(jī)理的生物進(jìn)化過程的計(jì)算模型，是一種通過模擬自然進(jìn)化過程搜索最優(yōu)解的方法[8-9]。遺傳算法是從代表問題可能潛在解集的一個(gè)種群（population）開始的，而一個(gè)種群則由經(jīng)過基因（gene）編碼的一定數(shù)目的個(gè)體（individual）組成。每個(gè)個(gè)體實(shí)際上是染色體（chromosome）帶有特征的實(shí)體。在初代種群產(chǎn)生之后，按照適者生存和優(yōu)勝劣汰的原理，逐代（generation）演化產(chǎn)生出越來越好的近似解，在每一代，根據(jù)問題域中個(gè)體的適應(yīng)度（fitness）大小選擇（selection）個(gè)體，并借助于自然遺傳學(xué)的遺傳算子（genetic operators）進(jìn)行組合交叉（crossover）和變異（mutation），產(chǎn)生出代表新的解集的種群。這個(gè)過程將導(dǎo)致種群像自然進(jìn)化一樣的后生代種群比前代更加適應(yīng)于環(huán)境，末代種群中的最優(yōu)個(gè)體經(jīng)過解碼（decoding），可以作為問題近似最優(yōu)解。

2.2 遺傳算法優(yōu)化Prony諧波檢測(cè)流程

利用遺傳算法優(yōu)化擴(kuò)展 Prony方法以實(shí)現(xiàn)對(duì)電力系統(tǒng)諧波檢測(cè)的目的，通過遺傳算法的尋優(yōu)過程可得出諧波參數(shù)（幅值A(chǔ)i、相位iφ、頻率fi以及衰減因子αi）的最優(yōu)取值。相應(yīng)的具體流程如下。

1）初始化。設(shè)置最大進(jìn)化代數(shù)T，隨機(jī)生成M個(gè)個(gè)體作為初始群體 P(0)，其中每個(gè)個(gè)體的維度為各個(gè)幅值A(chǔ)i、相位iφ、頻率fi以及衰減因子αi的個(gè)數(shù)之和，此外設(shè)置交叉規(guī)模 pn、交叉概率 pc與變異概率pm。

2）個(gè)體評(píng)價(jià)。計(jì)算基因群體P(t)中各個(gè)個(gè)體的適應(yīng)度值，其中t表示當(dāng)前進(jìn)化代數(shù)。

3）選擇運(yùn)算。將適應(yīng)度高的個(gè)體直接遺傳到下一代或是通過配對(duì)交叉以產(chǎn)生新的個(gè)體再遺傳到下一代，本文選擇俄羅斯輪盤賭的概率生成方式實(shí)現(xiàn)個(gè)體的選擇過程。

圖1 遺傳算法優(yōu)化Prony諧波檢測(cè)流程圖

4）交叉運(yùn)算。基于預(yù)先設(shè)定的交叉概率 pc對(duì)任意兩個(gè)個(gè)體進(jìn)行交叉操作以產(chǎn)生新的個(gè)體p*。

5）變異運(yùn)算。按照變異概率對(duì)群體中的某些個(gè)體上的某些基因位置上的染色體值進(jìn)行隨機(jī)變動(dòng)。

6）群體P(t)經(jīng)過選擇、交叉、變異運(yùn)算之后得到下一代群體P(t+1)。

7）終止條件判斷。若t=T，則為進(jìn)化過程中所得到的具有最大適應(yīng)度值的個(gè)體，并將其作為最優(yōu)解輸出，終止計(jì)算過程。

基于本文所提出的遺傳算法優(yōu)化 Prony諧波檢測(cè)方法，可以實(shí)現(xiàn)對(duì)輸入待檢測(cè)諧波信號(hào)的非線性擬合，同時(shí)以在線優(yōu)化參數(shù)機(jī)制克服了傳統(tǒng)諧波分析方法對(duì)諧波頻率無法精確估計(jì)的不足，有效提升諧波幅值以及相角的計(jì)算精度與穩(wěn)定性。

2.3 遺傳算法優(yōu)化Prony諧波檢測(cè)參數(shù)求解步驟

1）基于上式構(gòu)建樣本函數(shù) r(i,j)，并以此為基礎(chǔ)計(jì)算擴(kuò)展階數(shù)的方程矩陣形式，即

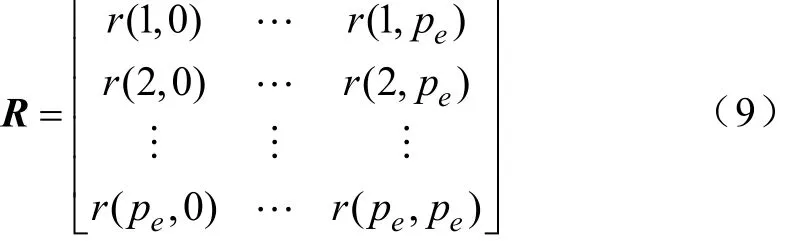
2）通過最小二乘估計(jì)確定矩陣 R的有效秩 p以及參數(shù)a1, a2,…, ap。

3）對(duì)多項(xiàng)式 1 + a z-1+ . ..+ a z-p= 0 計(jì)算其特征

p根 zk，1≤k≤p，令 x?( n ) = x(0)，計(jì)算參數(shù) b1, …, bp。4）利用諧波頻率建立遺傳算法優(yōu)化目標(biāo)函數(shù)，即

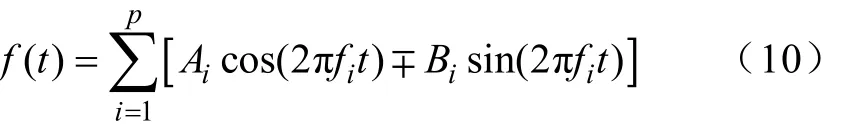
通過遺傳算法尋優(yōu)過程得出最優(yōu)解（Ai, Bi），i=1, 2, …, p，以此為基礎(chǔ)，算得諧波的幅值與相角。

電力諧波信號(hào)中往往含有隨機(jī)噪聲信號(hào)，基于傳統(tǒng) Prony諧波檢測(cè)方法所得到的各次諧波的幅值與相角存在比較大的誤差，這也是傳統(tǒng) Prony算法對(duì)實(shí)際諧波信號(hào)分析的局限性所在。利用遺傳算法的在線啟發(fā)式參數(shù)尋優(yōu)的優(yōu)勢(shì)，以及在曲線擬合方面的穩(wěn)定性強(qiáng)、精度高的優(yōu)點(diǎn)，構(gòu)建基于在線遺傳算法Prony參數(shù)尋優(yōu)的改進(jìn)Prony諧波檢測(cè)方法通過對(duì)輸入信號(hào)進(jìn)行非線性的擬合，計(jì)算出相應(yīng)的幅值與相角，同時(shí)對(duì)于頻率的估計(jì)精度有望改善和提升。

3 仿真實(shí)驗(yàn)

為了驗(yàn)證所提出的遺傳算法優(yōu)化 Prony電力諧波檢測(cè)方法的有效性，本文采用相關(guān)電力諧波檢測(cè)文獻(xiàn)中廣泛采用的算例，其中相應(yīng)的諧波模型信號(hào)為

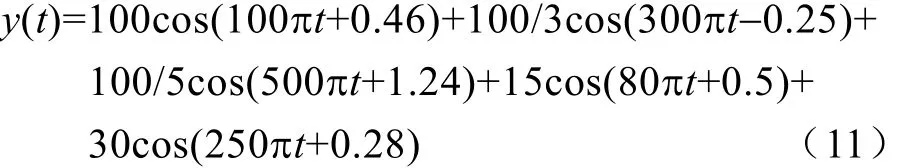
其中測(cè)試信號(hào)中含有基波、3次以及5次諧波，此外還含有40Hz和125Hz頻率的間諧波信號(hào)。取采樣頻率為1000Hz，其中采樣點(diǎn)數(shù)為50個(gè)，同時(shí)分別在 y(t)信號(hào)中疊加 50dB、40dB的白噪聲。在Matlab平臺(tái)上，分別對(duì)傳統(tǒng)的Prony諧波檢測(cè)方法以及本文所提出的遺傳算法優(yōu)化 Prony諧波檢測(cè)方法對(duì)測(cè)試信號(hào)進(jìn)行擬合，比較兩種方法的相關(guān)性能。對(duì)應(yīng)的擬合誤差結(jié)果如圖2和圖3所示。

圖3中，Prony諧波檢測(cè)方法在50dB信噪比條件下的平均誤差為 0.1310，在 40dB信噪比條件下的平均誤差為0.1523；而遺傳算法優(yōu)化Prony諧波檢測(cè)方法在上述不同信噪比下的平均誤差分別為0.0628與 0.0616。上述結(jié)果表明，信噪比變小對(duì)Prony諧波檢測(cè)方法具有不利影響，其擬合誤差有增大的趨勢(shì)，從而說明該方法對(duì)于信號(hào)中的噪聲較為敏感。而遺傳算法優(yōu)化 Prony諧波檢測(cè)方法擬合誤差平均值有顯著的下降，計(jì)算結(jié)果精度顯著改善（約為Prony方法的50%左右）；同時(shí)，該方法隨著信噪比的下降平均擬合誤差變動(dòng)不大，說明該方法對(duì)于引入的噪聲具有較好的抑制以及消除作用。此外，Prony檢測(cè)方法的擬合誤差在時(shí)間軸上分布不均，且有較大的分布區(qū)間，在50dB和40dB信噪比條件下的最大誤差值分別達(dá)到了0.4018和0.4326。

圖2 50dB信噪比下諧波檢測(cè)擬合誤差圖

圖3 40dB信噪比下諧波檢測(cè)擬合誤差圖

從圖4可知，本文所提出的遺傳算法優(yōu)化Prony諧波檢測(cè)方法在幅值估計(jì)值以及相角估計(jì)值的擬合誤差方面較傳統(tǒng)的 Prony諧波檢測(cè)方法具有顯著的優(yōu)勢(shì)。在信噪比為50dB時(shí)，遺傳算法優(yōu)化Prony諧波檢測(cè)方法基波分量幅值的絕對(duì)值誤差為 0.0236，而傳統(tǒng)的Prony諧波檢測(cè)方法的絕對(duì)誤差為0.0713，所提出的遺傳算法優(yōu)化 Prony諧波檢測(cè)的誤差精度下降了約66.7%；同時(shí)所提出的遺傳算法優(yōu)化Prony諧波檢測(cè)方法的相角誤差也明顯減少。

4 結(jié)論

本文以擴(kuò)展 Prony諧波檢測(cè)方法為基礎(chǔ)，針對(duì)其存在的噪聲條件下在線參數(shù)（包括幅值、相位、頻率以及衰減因子）匹配選擇問題，以啟發(fā)式遺傳算法對(duì)Prony諧波檢測(cè)相關(guān)參數(shù)進(jìn)行優(yōu)化選取，設(shè)計(jì)了相關(guān)了方法流程以及參數(shù)計(jì)算步驟。進(jìn)行與傳統(tǒng) Prony諧波檢測(cè)方法的仿真實(shí)驗(yàn)比較，結(jié)果顯示本文所提出的方法在擬合誤差精度、穩(wěn)定性等方面具有顯著的優(yōu)勢(shì)。

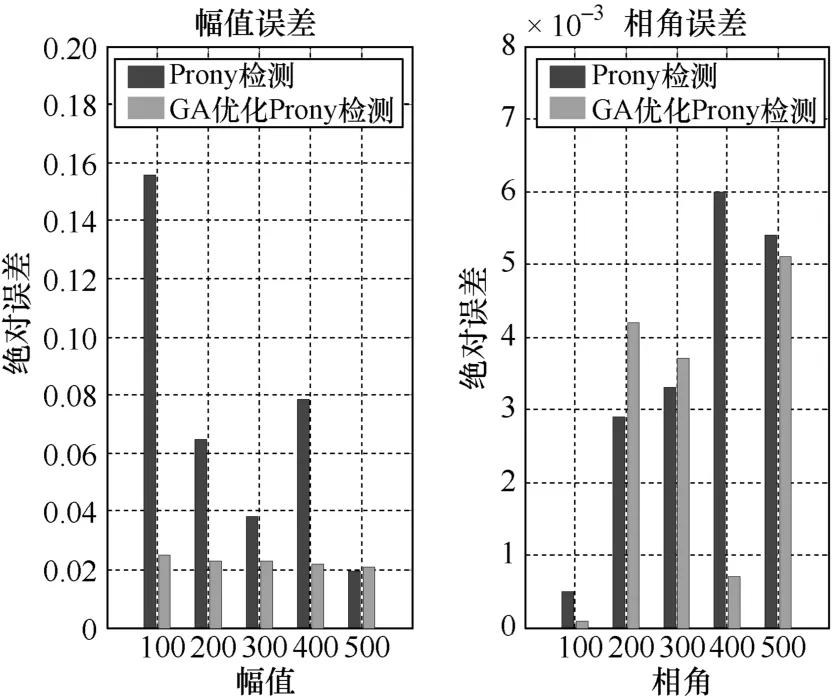
圖4 50dB信噪比下幅值與相角估計(jì)誤差

[1] 熊杰鋒, 李群, 袁曉冬, 等. 電力系統(tǒng)諧波和間諧波檢測(cè)方法綜述[J]. 電力系統(tǒng)自動(dòng)化, 2013, 37(11)：125-133.

[2] Asiminciaei L, Blaabjerg F, Hansen S. Detection is key-Harmonic detection methods for active power filter applications[J]. IEEE Industry Applications Magazine, 2007, 13(4)： 22-33.

[3] 楊洪耕, 惠錦, 侯鵬. 電力系統(tǒng)諧波和間諧波檢測(cè)方法綜述[J]. 電力系統(tǒng)及其自動(dòng)化學(xué)報(bào), 2010, 22(2)：65-69.

[4] 谷文靜, 金濤. 基于小波變換的電力系統(tǒng)諧波分析研究[J]. 電氣技術(shù), 2012, 13(8)： 36-40.

[5] 何巨龍, 王根平, 劉丹, 等. 配電系統(tǒng)諧波擾動(dòng)的定位與識(shí)別研究[J]. 電氣技術(shù), 2016, 17(12)： 25-30.

[6] 郭成, 李群湛, 賀建閩, 等. 電網(wǎng)諧波與間諧波檢測(cè)的分段Prony算法[J]. 電網(wǎng)技術(shù), 2010, 34(3)： 21-25.

[7] 陳曉芳, 趙成勇. 基于特定頻帶的Prony暫態(tài)振蕩檢測(cè)方法[J]. 電測(cè)與儀表, 2011(5)： 1-5.

[8] 王超學(xué), 田利波. 一種改進(jìn)的多目標(biāo)合作型協(xié)同進(jìn)化遺傳算法[J]. 計(jì)算機(jī)工程與應(yīng)用, 2016, 52(2)： 12-18.

[9] 葉滿園, 周琪琦, 蔡鴻, 等. 基于多種群遺傳算法的多電平逆變器多波段 SHEWM技術(shù)[J]. 電工技術(shù)學(xué)報(bào), 2015, 30(16)： 111-119.

Power System Harmonic Detection based on Prony Optimized by Genetic Algorithm

Ge Jianghong1Zhang Changli2
(1. State Grid Chuzhou Power Supply Company, Chuzhou, Anhui 239000;2. State Grid Wuhu Power Supply Company, Wuhu, Anhui 241000)

The realization of fast and accurate detection of power system harmonics is the key factor to effectively suppress harmonics, to improve power quality and enhance the stability of power grid. Through the comparison of the existing power system harmonic detection method, by analyzing the limitation of parameter optimization selection of the traditional Prony algorithm under noise conditions,and according to the fact that Prony algorithm can directly extract the characteristic parameters of the detected signal, and having the characteristics of strong adaptive ability, this paper proposes the power system harmonic detection method based on Prony optimized by genetic algorithm, in order to achieve the optimization selection of related parameters. Simulation results show that the proposed method has significant advantages in fitting error, accuracy and stability for harmonic detection signals under different signal-to-noise ratio conditions.

harmonic detection; genetic algorithm; prony algorithm

葛江紅（1972-），女，安徽滁州人，本科，工程師，研究方向?yàn)闊o功電壓電能質(zhì)量。