電氣彈簧關鍵負載電壓穩定的影響因素分析

詹 俊， 趙朝會， 王輝航

(上海電機學院 電氣學院, 上海 201306)

電氣彈簧關鍵負載電壓穩定的影響因素分析

詹 俊， 趙朝會， 王輝航

(上海電機學院 電氣學院, 上海 201306)

為分析電氣彈簧(ES)關鍵負載電壓穩定的影響因素，在分析ES工作原理的基礎上，借助數學推導研究了非關鍵負載電阻、輸電線阻抗、LC濾波器中電容/電感、電網頻率對關鍵負載電壓穩定的影響，并利用MATLAB/Simulink進行了仿真分析。仿真結果表明：當非關鍵負載電阻、輸電線阻抗、LC濾波器中電容增加時，ES能抑制的電壓波動范圍先增大后減小；當LC濾波器中電感增加時，ES能抑制的電壓波動范圍隨之增大；當電網頻率增加時，ES能抑制的電壓波動范圍逐漸減小。

智能負載; 電氣彈簧; 關鍵負載電壓; 影響因素

為緩解化石能源即將枯竭的危機，可再生能源得到了快速發展。可再生能源的發展使其有望成為全球電力的主要來源，但是，目前風能、太陽能等新能源發電的可控性較差，其發電量的不穩定性造成電網電壓波動和發電總量難以預測等問題[1-2]。為解決電壓波動的問題，研究人員提出了電力負荷管理的方法，如負荷調度[3]、實時電價[4]、電能存儲[5]、電力負荷控制[6-7]等，但這些方法不僅不能快速響應以緩解電壓波動，電能存儲的成本較高，且廢舊的電池和超級電容還會給環境帶來嚴重污染。

為更好地解決電壓波動的問題，文獻[8]中研究出了一種新型電力電子裝置——電氣彈簧(Electric Spring ，ES)，目前該技術已取得一定的研究成果。文獻[9]中對比研究了傳統機械彈簧與ES的物理模型，分析了ES的工作原理及其應用方向；文獻[10]中分析了ES的穩壓性，并通過改變非關鍵負載電流的相角，確定了ES電壓補償的范圍;文獻[11]中研究了一種相位控制算法，對ES進行了穩態性分析。當前ES的功能主要有穩定用戶側母線電壓[8]、穩定電網頻率[12-13]、功率因素校正[14]、抑制諧波[15]、平衡三相功率[16]等，其中，最重要的是穩定關鍵負載電壓，因此，分析ES關鍵負載電壓穩定的影響因素至關重要。

本文在分析ES工作原理的基礎上，借助數學推導研究了非關鍵負載電阻、輸電線阻抗、LC濾波器中電容/電感、電網頻率對關鍵負載電壓穩定的影響，并利用MATLAB/Simulink進行了仿真分析。

1 ES結構及其工作原理

1.1 ES結構

ES是由功率變換器和LC低通濾波器構成的。圖1所示為采用DC/AC變換器的ES拓撲和其在電網中的連接圖。在實際電網中,ES和非關鍵負載(Znc)串聯形成智能負載后，與關鍵負載(Zc)并聯接入電網。圖中，Ug為電網電壓；Us為關鍵負載電壓；UES、IES為ES中LC濾波器電容C的電壓、電流；IL為ES中LC濾波器電感L的電流;Inc為非關鍵負載的電流。

為了將電壓波動轉移至非關鍵負載上，故ES串聯非關鍵負載，通過改變非關鍵負載的功率消耗來實現發電量與用電量的平衡，從而確保關鍵負載的穩定運行。其中，關鍵負載是要求工作電壓穩定、且對電壓波動敏感的負載，如精密儀器、醫療儀器等；而非關鍵負載是輸入電壓范圍較大的負載，如照明系統、電冰箱、空調、電加熱器等。

(a) 拓撲結構圖

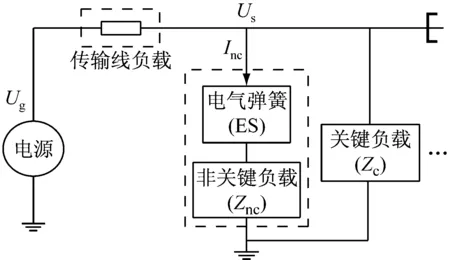
(b) 連接圖

1.2 ES的工作原理

ES在工作時，存在9種工作模式[17]，本文主要介紹兩種模式: ① 感性模式，即Ug發生波動導致Us高于理想值時，通過調節電流IES改變UES，使其超前Inc90°，由ES吸收無功功率來穩定Us；② 容性模式，即Us低于理想值時，通過調節IES改變UES，使其滯后Inc90°，由ES釋放無功功率來穩定Us。具體的物理關系式如下：

(1)

(2)

(3)

IES=IL+Inc

(4)

|SES|θES=|UES|·|Inc|(φES-φnc)

(5)

式中，q為電容C兩端的電荷量； |SES|、|UES|、|Inc|分別為ES輸出功率、輸出電壓、流進ES中電網電流的幅值；θES、φES、φnc為ES輸出功率、輸出電壓、流進ES中電網電流的相角。

2 影響ES關鍵負載電壓穩定的因素

ES的主要作用是穩定關鍵負載的電壓，因此，研究電路參數對ES調節性能的影響、對確保關鍵負載電壓的穩定有重要意義。

圖2所示為第二代ES的結構圖。

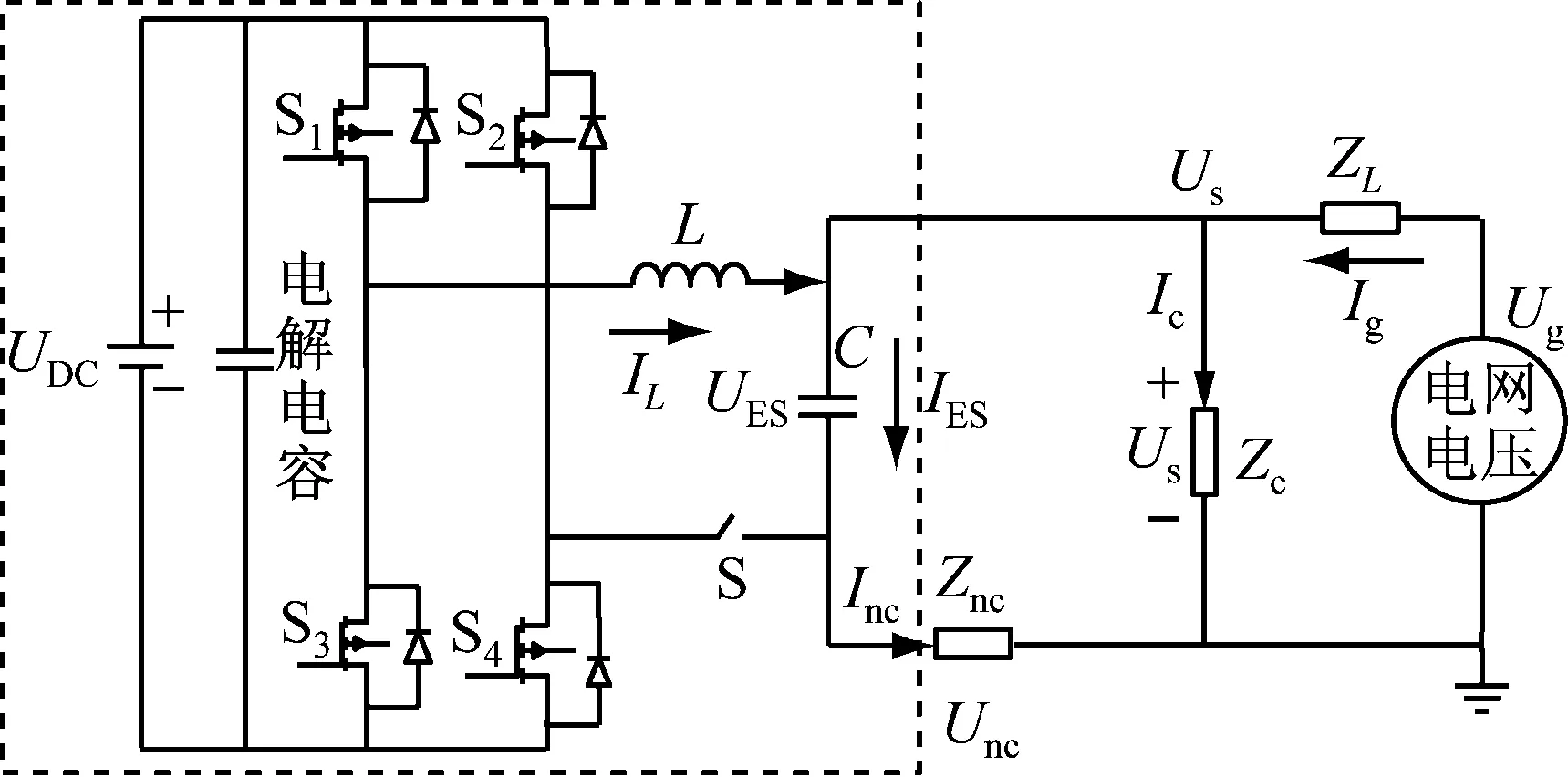
圖2 第二代電氣彈簧結構圖

為分析影響ES調壓的參數，對圖2中ES所在的支路列出如下電壓等式：

Us=UES+Unc

(6)

式中，Unc為非關鍵負載兩端的電壓，V。

由戴維寧定理將ES等效為一個電壓源和一個等效阻抗后，其開路電壓為

(7)

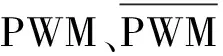
等效阻抗為

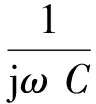
(8)

圖3所示為控制逆變器開關信號PWM的輸出波形，其中，Ts為輸出波形的周期。

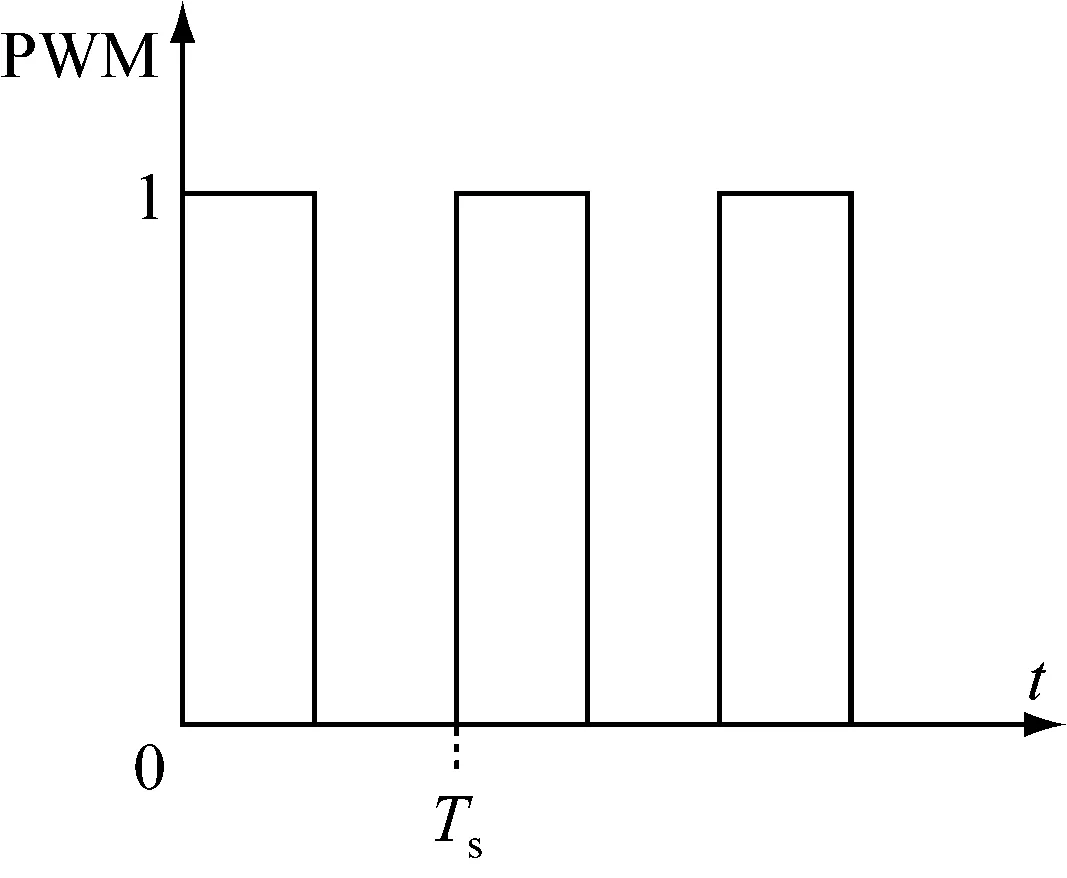
圖3 PWM的輸出波形

式(6)可轉換為

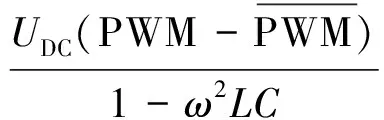
(9)

式中，Znc為非關鍵負載的阻抗，Ω。又由于

Ug=Us+IgZL=Us+(Inc+Ic)ZL

(10)

Ic=Us/Zc

(11)

式中，Ig為電網電流；IL為電網輸電線的阻抗；Zc、Ic分別為關鍵負載的阻抗、電流。故非關鍵負載電流為

Inc=(Ug-Us)/ZL-Us/Zc

(12)

將式(12)代入式(9)可得

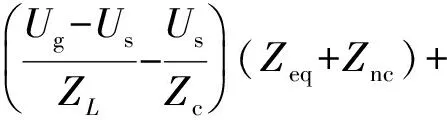
(13)

整理后得到

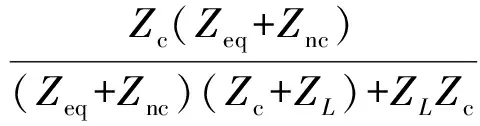
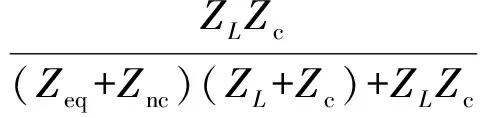
(14)

由式(14)可見，影響ES關鍵負載電壓穩定的因素有Znc、ZL、C、L、ω。由于ω為電網角頻率而非電網頻率f，根據ω=2πf的比例關系，故可將對ω的分析轉換成對f的分析。

3 仿真分析

為分析Znc、ZL、C、L、f對ES關鍵負載電壓穩定的影響，本文進行了仿真研究。圖4所示為仿真控制框圖。

根據圖4在MATLAB/Simulink中建立了仿真模型,仿真分析了Znc、ZL、C、L、f變化時，對ES關鍵負載電壓穩定的影響。仿真實驗中，通過PI環節保證Us跟蹤參考電壓來實現穩定關鍵負載電壓的目標；此外，在控制環節中額外增加了一階低通濾波環節和諧波補償環節來降低Us的諧波含量。其中，PI環節中比例系數kp=50,積分系數kI=5，powergui為離散模式，Ts=10 μs，仿真時間為1 s。諧波補償環節中的濾波器為MATLAB/Simulink庫中的帶通濾波器，由于基波頻率為50 Hz，故仿真中帶通濾波器的通帶頻率設置為45～55 Hz。

(1)Znc的影響。由于感/容性負載中電感/電容的變化對ES 調壓性能的影響不大，故分析電阻型非關鍵負載對ES調壓的影響。改變Znc，其他仿真參數如下：C=1.32 mF,L=5 mH，Zc=43.2 Ω，ZL=0.2+0.023j Ω，UDC=600 V，f=50 Hz，進行仿真實驗。圖5所示為Znc=30 Ω時，部分Ug和Us有效值波形。

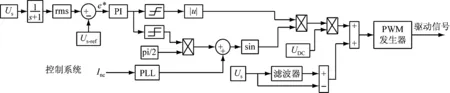
圖4 無功補償控制框圖

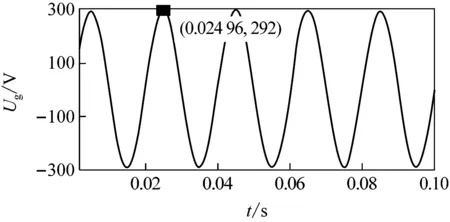
(a) Ug=292 V時，Ug波形

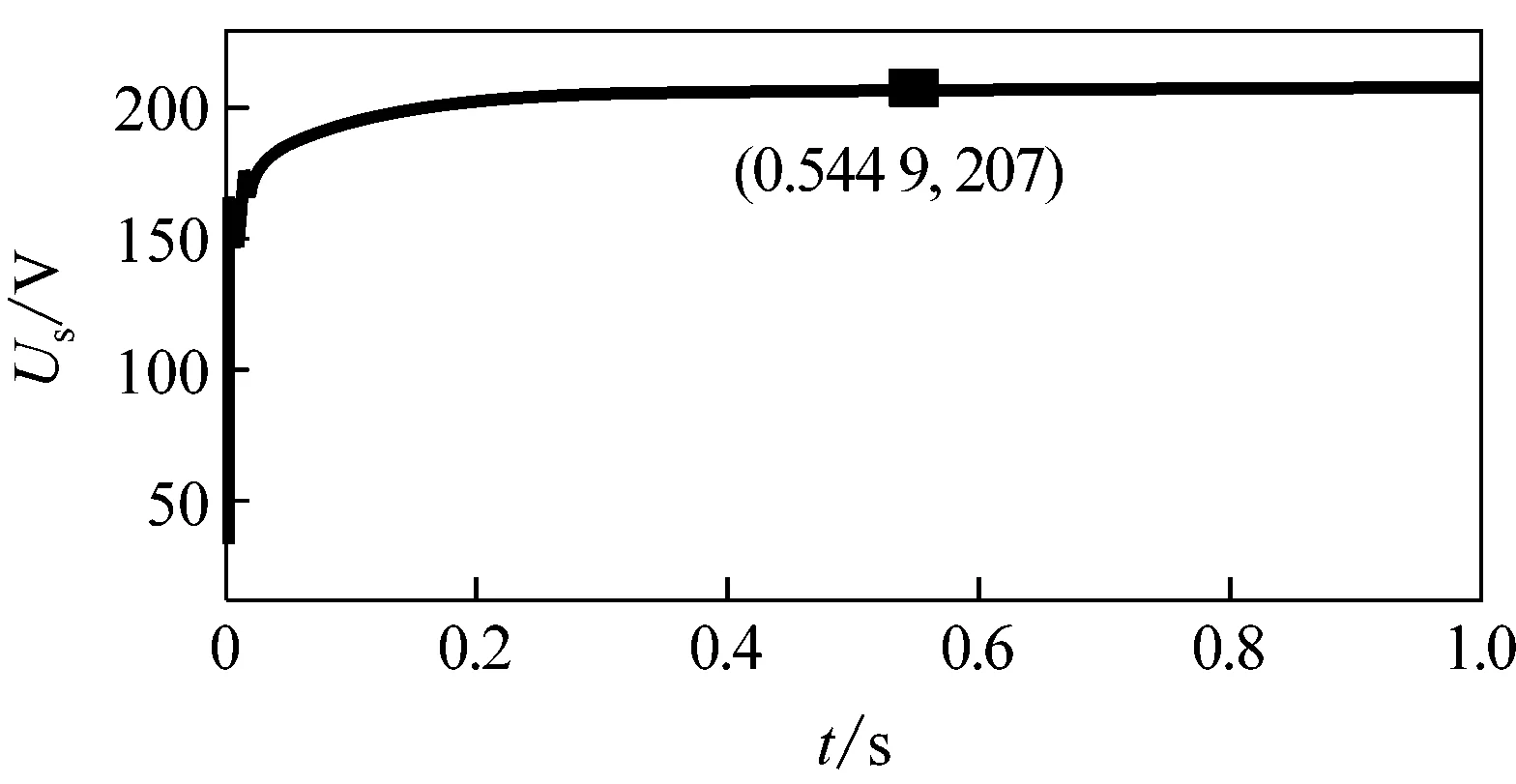
(b) Ug=292 V時，Us波形

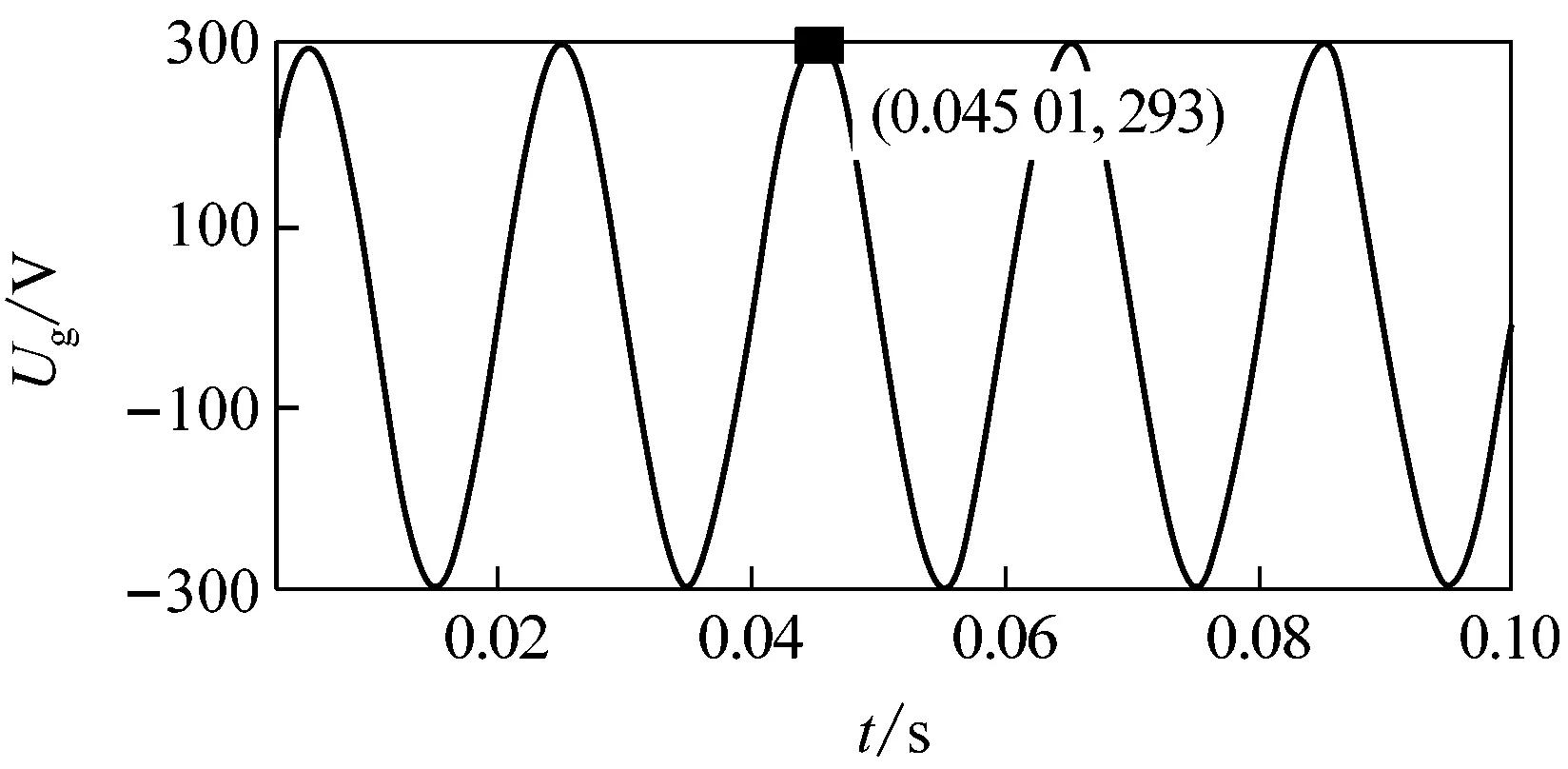
(c) Ug=293 V時，Ug波形

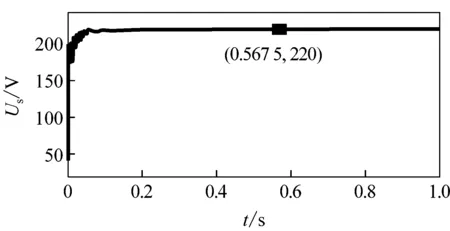
(d) Ug=293 V時，Us波形

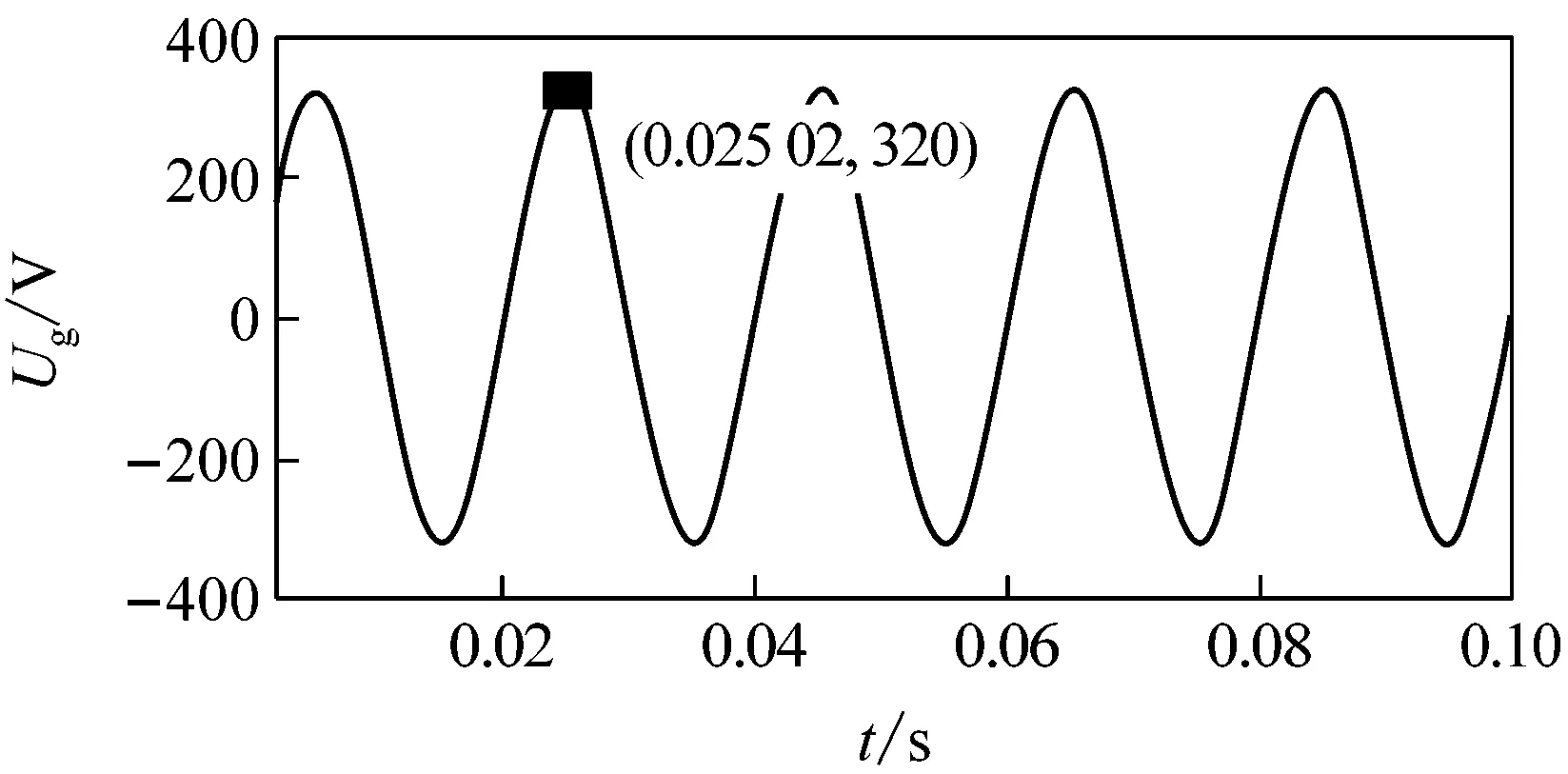
(e) Ug=320 V時，Ug波形

(f) Ug=320 V時，Us波形

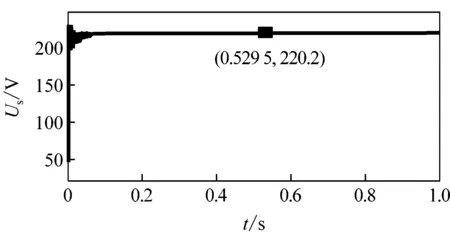
(h) Ug=483 V時，Us波形

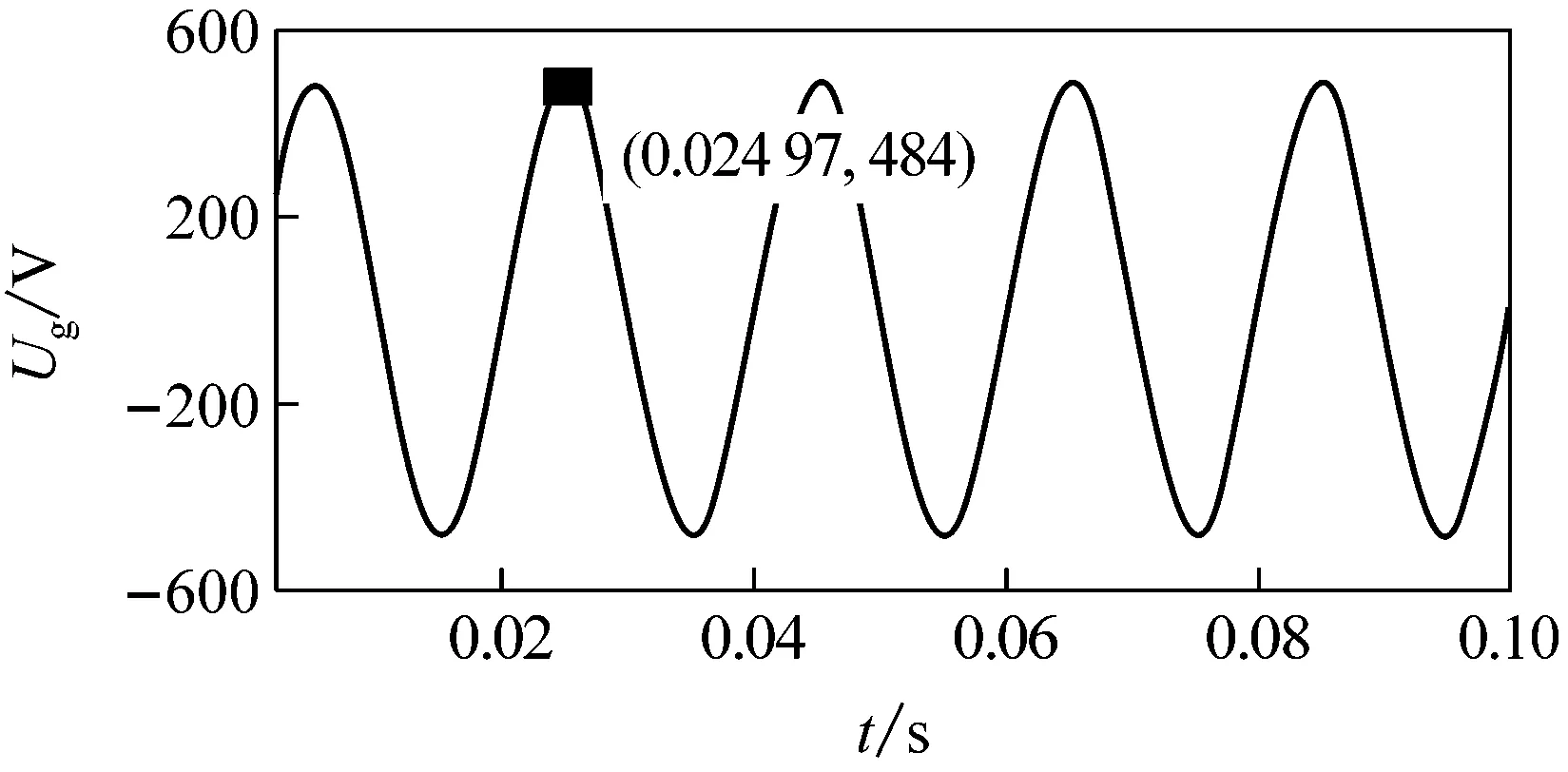
(i) Ug=484 V時，Ug波形

續圖5當Znc=30Ω時，Ug波形和ES工作后，關鍵負載電壓有效值波形

Fig.5 Waveform ofUgwhenZncis 30 Ω, and that of RMS voltage on the critical load when ES is activated

由圖可知，當Ug為292、484 V時，ES工作后的Us有效值分別為207 V和250.1 V，都不能將Us調至220 V；而當Ug為293、483、320 V(取293～483 V間任意值)時，ES工作后的Us都能被調至220 V；由此可確定， 293 V和483 V分別為ES能抑制的電壓的下限和上限值，即Znc=30 Ω時，ES的電壓補償Ug的范圍為293～383 V。

由于篇幅有限，本文省略其他仿真波形，得到Us穩定情況下，Znc變化時，Ug的波動范圍如表1所示，Ug波動范圍內的長度變化如圖6所示。

表1 當Znc變化時，Ug的波動范圍

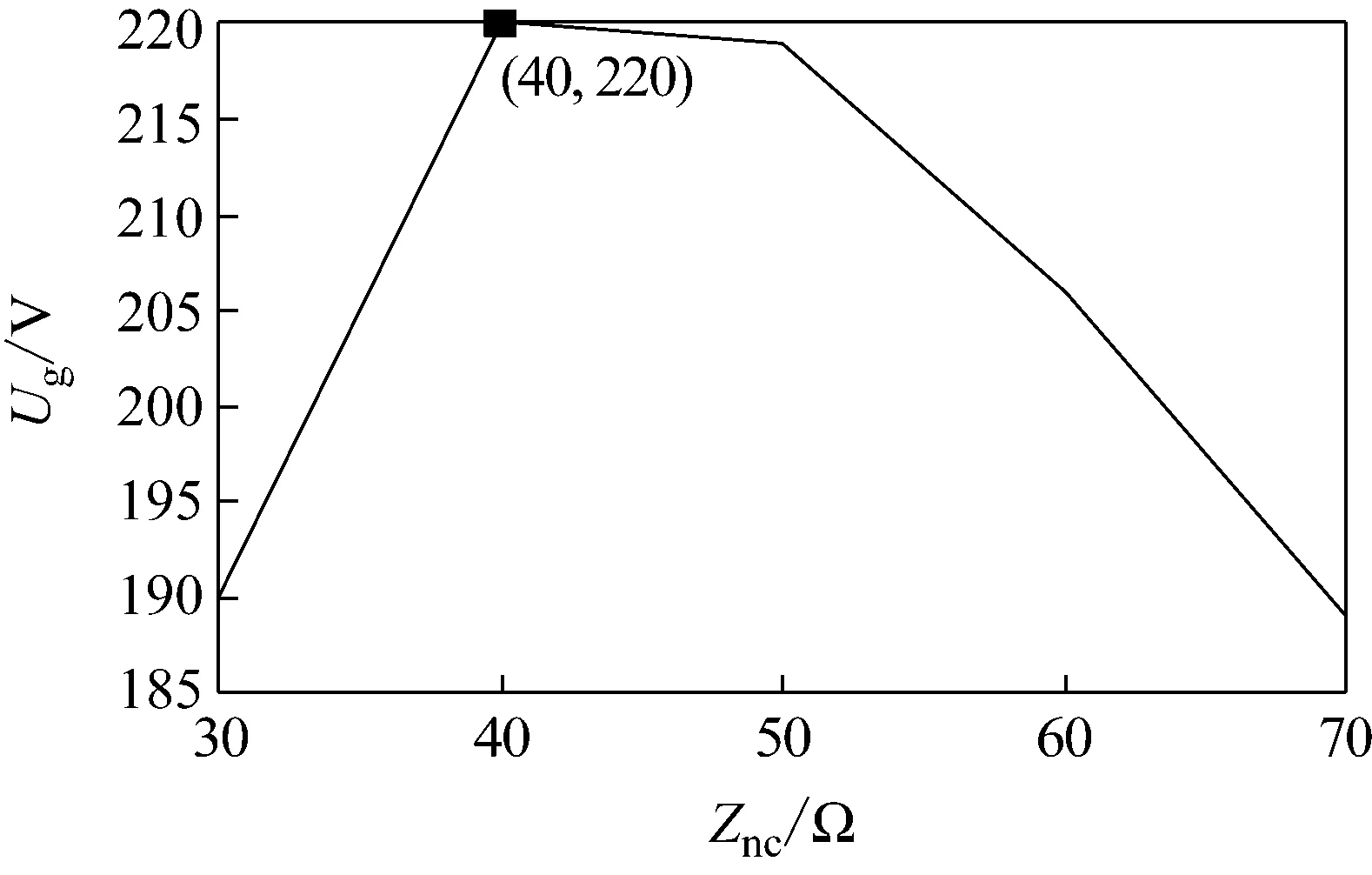
圖6 非關鍵負載的電阻發生變化時，Ug波動范圍內的長度變化

由表1和圖6可見，當Znc=30，40，50，60，70 Ω時，ES的電壓補償Ug波動長度分別為190、220、219、206、189 V，可見，隨著Znc的增加，ES可抑制的電壓波動范圍先增大后減小。

(2)ZL的影響。改變ZL，其他仿真參數如下：C=1.32 mF,L=5 mH,Znc=50 Ω，Zc=70 Ω,UDC=800 V,f=50 Hz，進行仿真實驗。為確保Us穩定，當ZL變化時，得到Ug的波動范圍如表2所示，Ug波動范圍內的長度變化如圖7所示。

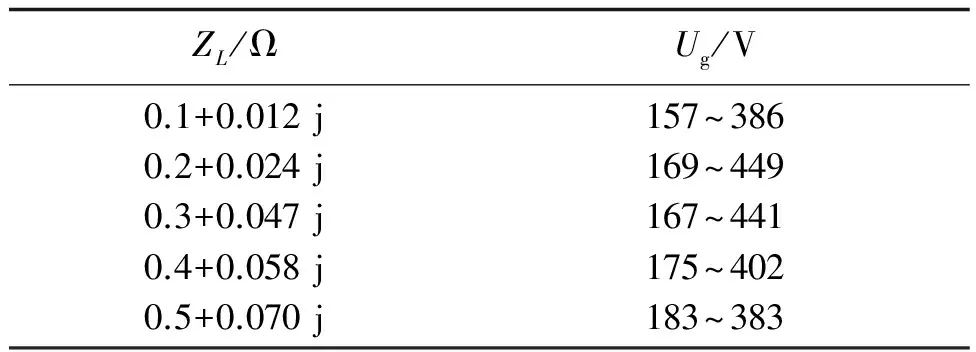
表2 當ZL變化時，Ug的波動范圍

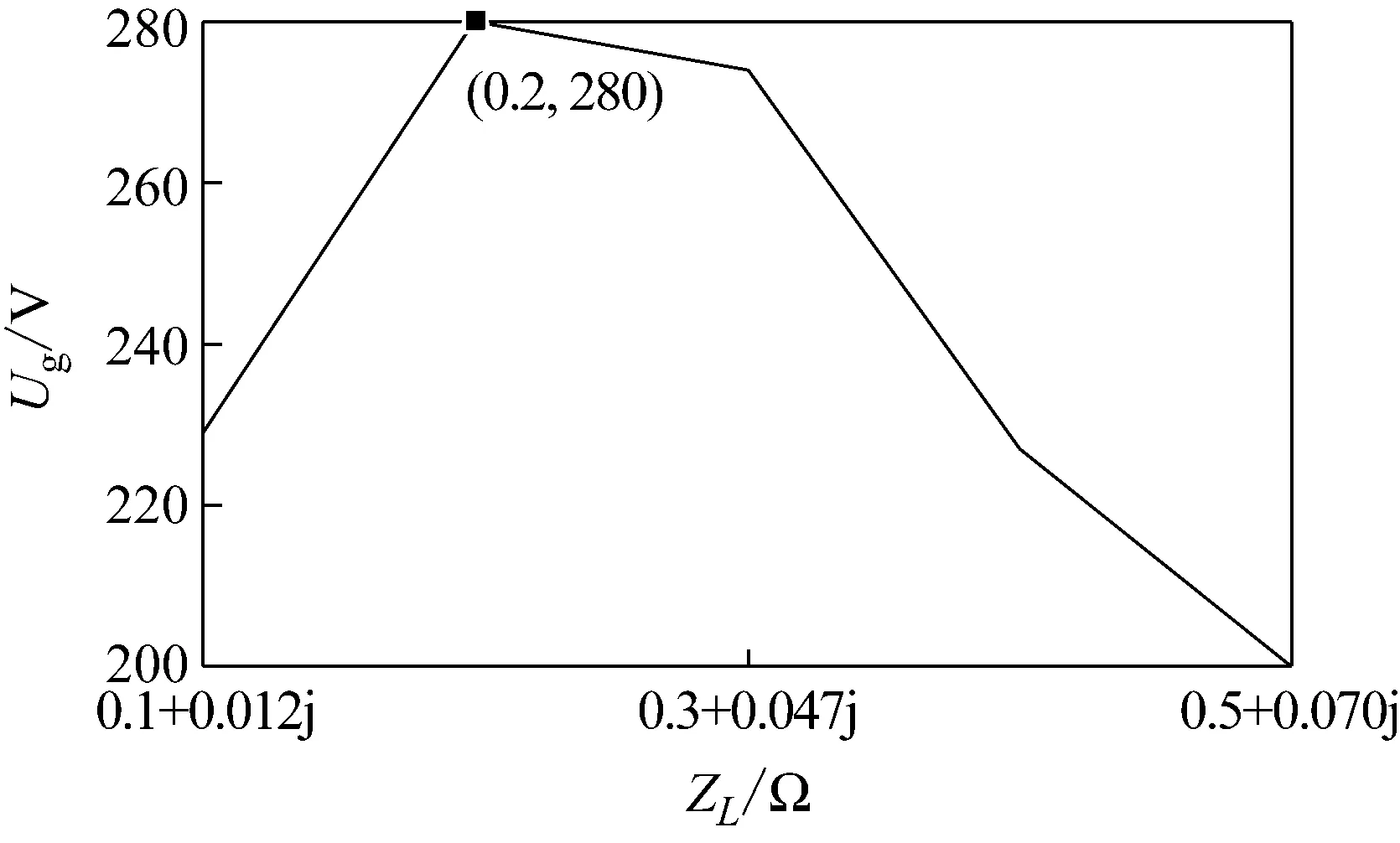
圖7 當ZL變化時，Ug波動范圍內的長度變化

由表2、圖7可見，當ZL= 0.1+0.012j，0.2+0.024j，0.3+0.047j，0.4+0.058j，0.5+0.070j Ω時，ES工作后，Ug波動長度分別為229、320、200 V，可見，隨著ZL的增加，ES可抑制的電壓波動范圍先增大后減小。

(3)C的影響。改變LC濾波器中的C值，其他仿真參數如下：L=0.5 mH,Znc=50 Ω,Zc=43.2 Ω,ZL=0.2+0.023j Ω,UDC=600 V,f=50 Hz，進行仿真實驗。為確保Us穩定，得到Ug的波動范圍如表3所示，Ug波動范圍內的長度變化如圖9所示。

表3 當C變化時，Ug的波動范圍

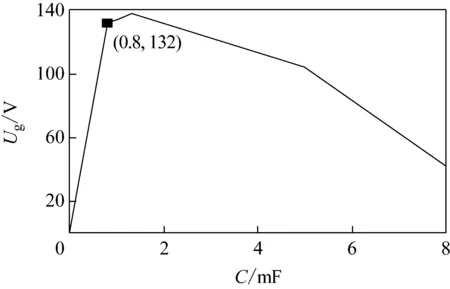
圖8 當LC濾波器中C變化時，Ug波動范圍內的長度變化

由表3、圖8可見，當LC濾波器中的C=0.80，1.00，1.32，5.00，8.00 mF時，Ug波動長度分別132、134、138、104、42 V，可見，隨著C的增加，ES可抑制的電壓波動范圍先增大后減小。

(4)LC濾波器中L的影響。改變LC濾波器中L的值，其他參數如下：C=1.32 mF,Znc=50 Ω，ZC=70 Ω,ZL=0.2+0.023j Ω，UDC=600 V,f=50 Hz，進行仿真實驗。為確保Us穩定，得到Ug波動范圍如表4所示，Ug波動范圍內的長度變化如圖10所示。

由表4、圖9可見，當L=0.1，0.9，1.0，2.5，5.0 mH時，Ug波動范圍內的長度為129、148、151、191、220 V，可見，隨著L的增加，ES可抑制的電壓波動范圍也在增大。

(5)f的影響。改變f，其他仿真參數如下：C=5 mF,L=0.5 mH,Znc=50 Ω,ZC=43.2 Ω,ZL=0.2+0.023j Ω,UDC=600 V，進行仿真實驗。為確保Us穩定，得到Ug波動范圍表如5所示，Ug波動范圍內的長度變化如圖11所示。

表4 當L變化時，Ug的波動范圍

圖9 當LC濾波器中L變化時，Ug波動范圍內的長度變化

由表5、圖10可見，當ω= 44，47，50，53，56 Hz時，Ug波動范圍內的長度分別為110、106、104、99、97 V，可見，隨著f的增加，ES可抑制的電壓波動范圍逐漸減小。

表5 當f變化時，Ug的波動范圍

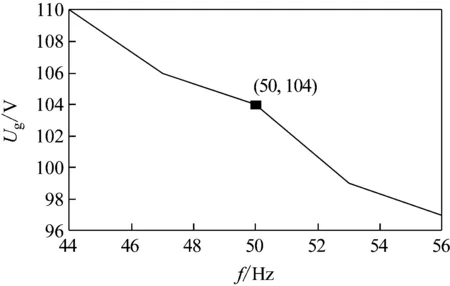
圖10 電網頻率發生變化時，Ug波動范圍內的長度變化

4 結 論

本文對ES工作原理進行分析，借助數學推導，研究了ES對Us穩定的影響因素，最后通過仿真得出以下結論：

(1) 影響Us穩定的因素有Znc、ZL、C、L、f。

(2) 在確保Us穩定的前提下，當Znc、ZL、C、L、f發生變化時，ES可抑制的Ug波動范圍會發生改變，超出該范圍,ES將無法確保Us的穩定，具體表現為隨著Znc、ZL、LC濾波器中C的增加，ES可抑制的Ug波動范圍先增大后減小；隨著LC濾波器中L的增加，ES可抑制的Ug波動范圍也逐漸增大；隨著f的增加，ES可抑制的Ug波動范圍逐漸減小。

[1] 白建華,辛頌旭,劉俊,等.中國實現高比例可再生能源發展路徑研究 [J].中國電機工程學報,2015,35(14):3699-3705.

[2] 孫濤,王偉勝，戴慧珠，等．風力發電引起的電壓波動和閃變 [J]．電網技術，2003，27(12)：62-66．

[3] MOHSENIAN-RAD A H，WONG V W S，JATSKEVICH J，et al. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid [J]. IEEE Transactions on Smart Grid, 2010(3):320-331.

[4] CONEJO A J, MORALES J M, BARINGO L. Real-time demand response model [J].IEEE Transactions on Smart Grid, 2010(3):236-242.

[5] 林海雪. 現代儲能技術應用概況及展望 [J].電源學報，2015，13(5)：34-40.

[6] LEE S C, KIM S J, KIM S H. Demand side management with air conditioner loads based on the queuing system model [J].IEEE Transactions on Power Systems,2011,26(2):661-668.

[7] 周潮，邢文洋，李宇龍. 電力系統負荷預測方法綜述 [J].電源學報,2012，10(6)：32-39.

[8] HUI S Y, LEE C K, WU F F. Electric springs-A new smart grid technology [J].IEEE Transactions on Smart Grid,2012,3(3):1552-1561.

[9] 卓克瓊,趙朝會,王飛宇,等.電氣彈簧的原理及發展[J].上海電機學院學報,2016,19(1):12-17.

[10] WEI Xile, LIU Yang, ZHANG Zhen, et al. Steady-state analysis of electric spring for smart grid [C]// 12th World Congress on Intelligent Control and Automation. Guilin, China: IEEE, 2016:905-909.

[11] WANG Qingsong, CHENG Ming, CHEN Zhe, et al. Steady-state analysis of electric springs with a novel δ control [J]. IEEE Transactions on PowerElectronics, 2015,30(12):7159-7169.

[12] CHAKRAVORTY D, CHAUDHURI B, HUI S Y R. Rapid frequency response from smart loads in great Britain power system [J]. IEEE Transactions on Smart Grid,2017,8(5): 2160-2169.

[13] AKHTAR Z, CHAUDHURI B, HUI S Y R. Primary frequency control contribution from smart loads using reactive compensation [J].IEEE Transactions on Smart Grid,2015,6(5):2356-2365.

[14] SONI J, PANDA S K. Electric spring for voltage and power stability and power factor correction [C]// 2015 9th International Conference on Power Electronics and ECCE Asia. Seoul, Korea: IEEE, 2015:2091-2097.

[15] WANG Qingsong, CHENG Ming, JIANG Yunlei. Harmonics suppression for critical loads using electric springs with current-source inverters [J].IEEE Journal of Emerging & Selected Topics in PowerElectronics,2016,4(4):1362-1369.

[16] YAN S, TAN S C, LEE C K, et al. Reducing three-phase power imbalance with electric springs [C]//2014 IEEE 5th International Symposium on Power Electronics for Distributed Generation Systems. Galway, Ireland:IEEE, 2014:1-7.

[17] 詹俊,趙朝會,卓克瓊，等.電氣彈簧技術的現狀與發展 [J].上海電機學院學報,2017,20(2):86-97.

Influencing Factors for Stabilizing Voltage on Critical Loads of Electric Spring

ZHANJun,ZHAOChaohui,WANGHuihang

(School of Electrical Engineering, Shanghai Dianji University, Shanghai 201306, China)

To study the influencing factors for stabilizing voltage on critical loads of an electric spring ES, the principle of (ES) is analyzed. By mathematical derivation, the effects of non-critical resistance load, impedance of the power line, capacitance/inductance in theLCfilter, and frequency of the power grid on the voltage stability of critical load are studied. MATLAB/Simulink was used in the analysis. The results show that, with increase of non-critical load resistance, impedance of the transmission line and capacitance of theLCfilter, the range of voltage fluctuation that ES can suppress increases first, and then decreases. With the increase of inductance ofLCfilter, the range of voltage fluctuation that ES can suppress increases. As the frequency of the power grid increases, the range of voltage fluctuation that ES can suppress gradually decreases.

smart load; electric spring (ES); critical load voltage; influence factor

2017 -09 -25

上海市教育委員會科技創新項目資助(13AZ01)

詹俊(1991-)，男，碩士生，主要研究方向為電力電子與電力傳動，E-mail: 1397654759@qq.com

2095 - 0020(2017)06 -0335 - 07

TM 761

A