基于誤差修正的極端學習機超短期風速預測

潘羿龍， 丁云飛

(上海電機學院 電氣學院， 上海 201306)

基于誤差修正的極端學習機超短期風速預測

潘羿龍， 丁云飛

(上海電機學院 電氣學院， 上海 201306)

超短期風速預測對風電場功率預報系統的建立和運行至關重要。針對具有較大隨機波動性的風速預測，研究了一種基于誤差修正的極端學習機(ELM)超短期風速預測方法。利用ELM模型對風速進行初步預測，并利用由此得到的誤差數據樣本建立差分自回歸滑動平均模型(ARIMA)，進行誤差預測，最后使用預測誤差對風速的初步預測值進行補正，從而求得最終預測值。仿真實驗結果表明，該方法在風速超短期預測中的可行性及有效性。

風速預測； 預測誤差補正； 極端學習機； 差分自回歸滑動平均模型

隨著風電裝機容量的不斷增加以及大規模的風電并網運行，風速的間歇性和隨機性變化勢必會對電力系統的安全運行帶來嚴峻挑戰[1]。因此，風速預測作為風力發電的基礎，對電網的可靠運行具有舉足輕重的意義，受到了越來越多的關注[2]。

從時間尺度上講，風速的預測可分為長期、中期、短期以及超短期預測[3]。其中，長期預測是對一年或更長時間的預測，主要用于風電場選址與建設；中期預測為一周或數周內的風速預測，主要用來擬定風電機組檢修計劃；短期預測為48～72 h內的風速預測，主要用于電力調度部門的調度；超短期預測為4 h以內的風速預測，主要為風電機組的控制以及為電力實時調度系統提供參考。同時，超短期風速預測對電網并網運行也有重要作用，預測精度越高，實時調度系統做出的判斷就越準確，對備用機組的選擇也就越準確[4]。

對于風速的預測方法主要有時間序列法[5]、人工神經網絡法[6]以及組合預測法[7]等，在預測效果上各有優、缺點。為提高風速的預測精度，各種組合預測方法受到了越來越多的關注，文獻[8-10]中用時間序列分別與馬爾科夫鏈、卡爾曼濾波、神經網絡等方法組合進行風速預測。文獻[11]中將最小二乘支持向量機(Least Squares Support Vector Machines,LS-SVM)與自回歸滑動平均模型(Autoregressive Moving Average Model, ARMA)相結合，對風速進行短期預測。上述組合方法通過分攤單獨預測的誤差風險來減小大偏差對最終預測值的影響，但是，加權系數的強壯性一直是組合方法的瓶頸[12]。目前，更多學者關注的是通過改進算法本身來提高模型的預測精度。文獻[13]中將LS-SVM與誤差補正結合起來，提高了風速的預測精度。文獻[14]中通過引入天氣預報數值，利用BP神經網絡與SVM相結合的方法對風速進行預測，獲得了較好的效果。

極端學習機(Extreme Learning Machine，ELM)是近期發展起來的一種前饋神經網絡方法，輸入權值在訓練過程中不需要多次調整，具有計算速度快、訓練過程簡單、抗干擾能力強等優點[15]，在實際操作中，有較高預測精度[16]。將ELM與時間序列方法組合起來可以在較短的時間內獲得風速的預測值，為實時調度提供更好的幫助。

為了減少風速的預測誤差，本文用ELM做初步預測時所獲得的誤差作為原始數據，導入差分自回歸滑動平均模型(Autoregressive Integrated Moving Average Model,ARIMA)，獲得誤差預測值；并用該誤差預測值對ELM的初步預測結果進行誤差修正，以提高風速的預測精度。仿真實驗結果表明，該方法在實際應用中具有一定的優勢。

1 極端學習機(ELM)

ELM是一種前饋單隱層神經網絡，圖1所示為ELM網絡結構。圖中，J、K、L分別為輸入層、隱含層、輸出層的神經元個數，其中，j=1,2,…,J；k=1,2,…，K；l=1,2,…，L；ωjk為輸入層第j個神經元與第k個隱含層神經元的權重；βkl為第k個隱含層神經元與第l個輸出層的權重；X=[x1,x2,…,xJ] 為輸入向量;Y=[y1,y2,…,yL]為輸出向量,xJ、yL分別為輸入、輸出值。

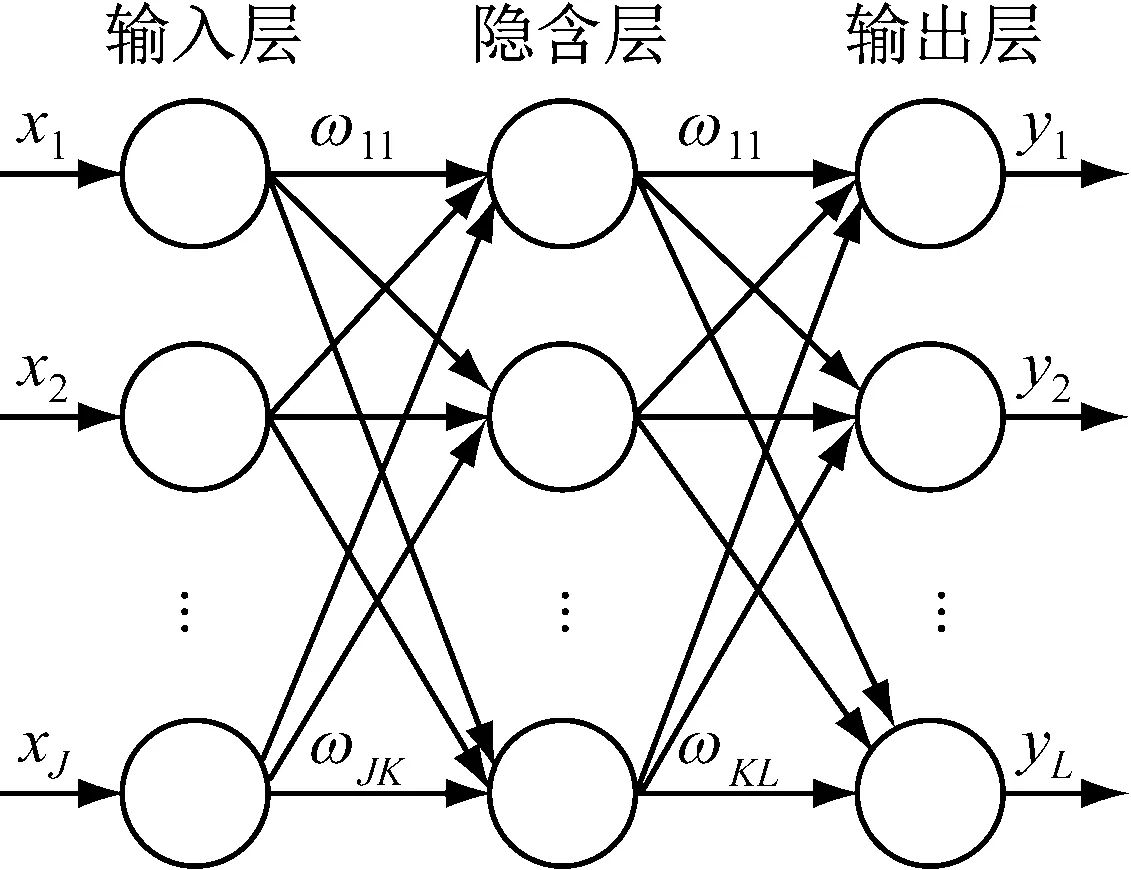
圖1 ELM網絡結構

在確定了隱含層的激活函數f(x)后，ELM的訓練輸出向量為

T=[t1,t2,…,ti,…,tn]L×n,i∈L

其中，n為數據維數；ti為訓練輸出，

(1)

式中,ψk=[ωj1,ωj2,…,ωjK]為第j個輸入神經元與隱含層的權值向量；bk為第k個隱含層的偏置;f(ψk,bk,xj)為第k個隱含層神經元輸出，f(ψk,bk,xj)=f(ψkxj+bk)，激活函數可選擇sigmoid或sine函數。

若ELM能以零誤差逼近學習樣本，則可以認為存在βk=[β1l,β2l,…,βKl]、ψk、bk，使

(2)

成立。

將式(2)改寫成矩陣形式，

Hβ=Y

(3)

式中，H為隱含層輸出矩陣；β為權值矩陣；Y為輸出矩陣。這樣上述問題就變成了求輸出權值的最小二乘解β問題[17]，即

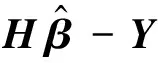
(4)

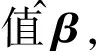
2 ARIMA

ARIMA又稱為Box-Jenkins模型，是一種基于時間序列的預測模型，適用于短期和超短期預測，精度較高[4]。ARIMA模型先對數據進行d階差分處理,使其平穩化，然后對平穩化序列建模,即得到ARMA,

(5)

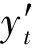
在估計自回歸系數、滑動平均系數時，最常用的是最小二乘法，可得到δg、θh；并根據赤池信息準則(Akaike Information Criterion，AIC)進行定階，得到p、q[18]。

3 基于ARIMA修正的ELM預測模型

由于風速的隨機、不穩定性，故在利用歷史數據進行預測時，會產生誤差。誤差修正模型可以對當前的預測方法進行補充，結合預測方法的優勢，可以更好地對風速進行預測。

3.1 基于誤差修正的超短期風速預測流程

圖2所示為基于誤差修正的超短期風速預測流程圖。具體步驟如下：① 先對風速的歷史數據做歸一化處理；② 將處理后的數據分為訓練集D1、測試集D2和預測集D3，并用訓練集D1對ELM訓練，用確定好的ELM模型對測試集D2、預測集D3進行預測；③ 用預測集D1對ELM做訓練，用測試集D2對ELM做測試，將獲得的訓練誤差和測試誤差作為誤差數據；④ 判斷序列是否平穩，若平穩，則使用ARMA模型，若不平穩，則使用ARIMA模型；⑤ 將初步預測值與誤差預測值疊加獲得最終風速預測值。

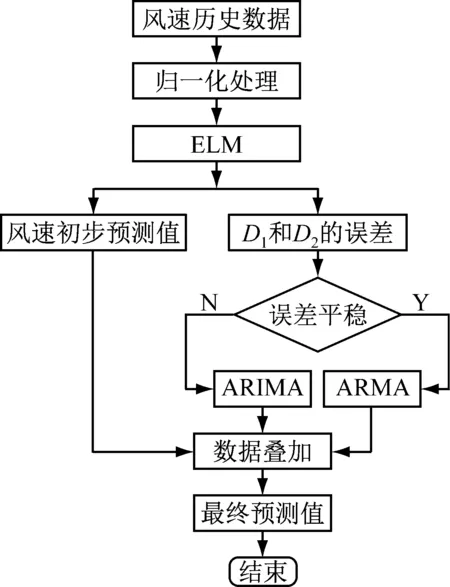
圖2 超短期風速預測流程圖

(1) 對原始數據進行歸一化處理。遠離零區域的數據會對學習速度造成影響，故在訓練前要對數據進行歸一化處理。本文將風速原始數據映射到[0,1]內，訓練結束后再反映射回原數據空間，即

(6)

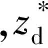
(2) ELM參數選取。當用大量的歷史數據進行學習時，ELM可有效地提高預測模型的預測精度。與傳統SVM相比，ELM在進行模型訓練時還具有較快的運算速度。

圖3所示為ELM參數選擇流程圖。

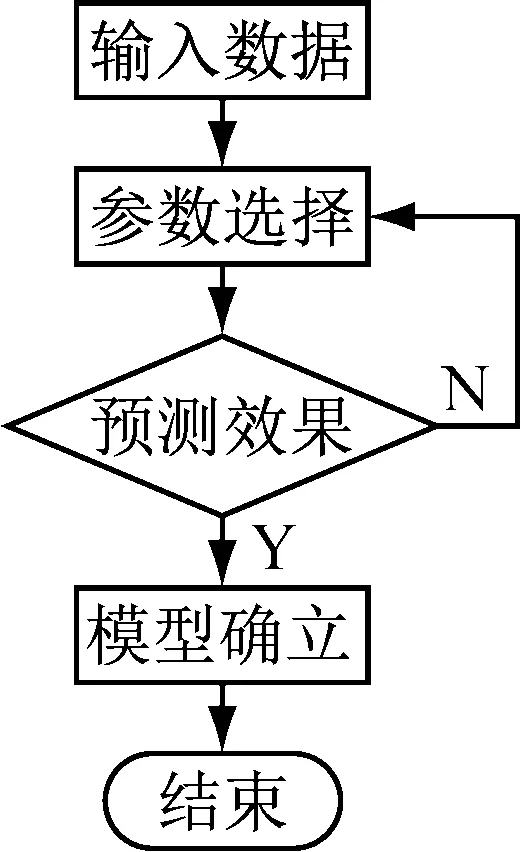
圖3 ELM參數選擇流程

在進行ELM訓練時，以ELM輸出誤差與真實值之比作為評價標準判斷ELM模型的好壞。ELM訓練步驟如下：① 進行ELM初始化。本文選取sigmoid函數為激活函數，隨機產生輸入權值Г、隱含層偏置B，并根據實驗確定隱含層神經元的個數，完成ELM網絡初始化；② 根據誤差率的大小作為評價標準來評價ELM初步預測結果的好壞，多次運行程序，選取其中較好的結果所對應的ELM參數作為模型參數；③ 應用確定好的ELM模型進行風速初步預測。

(3) 輸入數據平穩性判別。 單位根檢驗由Dickey-Fuller于1979年提出，主要用來驗證時間序列是否存在單位根，若數據小于顯著性水平α，則認為不存在單位根，即數據平穩[19]。本文使用目前使用較多的判斷方法——增廣DF檢驗(Augmented Dickey-Fuller，ADF)[19]來進行輸入數據的平穩性判別。

(4) 誤差擬合預測。圖4所示為誤差數據預測圖。具體過程如下：① 根據自相關、偏相關圖估計p、q的大致取值；② 根據AIC準則選取最優p、q值；③ 建立ARIMA模型進行誤差預測。

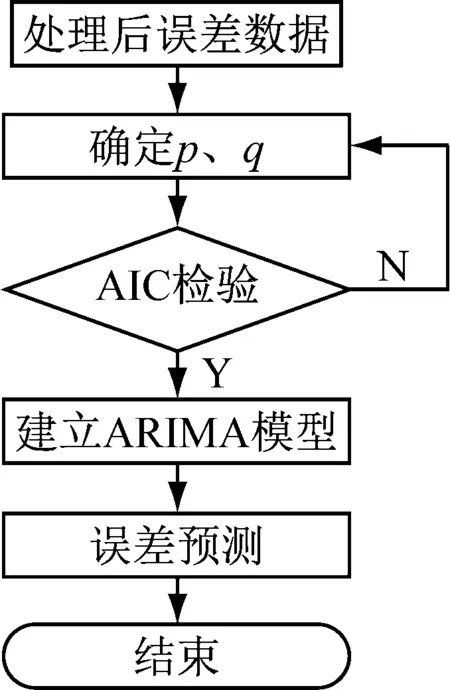
圖4 誤差數據預測流程

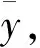
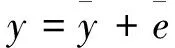
(7)

4 仿真結果與分析

為驗證本文方法的可行性，對東北某電廠2007-04-07—2007-04-11采集的風速數據進行分析，采集高度為71 m，每10 min記錄一次，共計720個數據；其中，前576個數據用于數據訓練，中間132個數據用于測試，后面12個數據用于最終預測。

圖5為720個風速數據的折線圖。圖中，n為數據個數。其中，最大風速值vmax=14.02 m/s，最小風速值vmin=0.35 m/s，可見，風速波動較大。

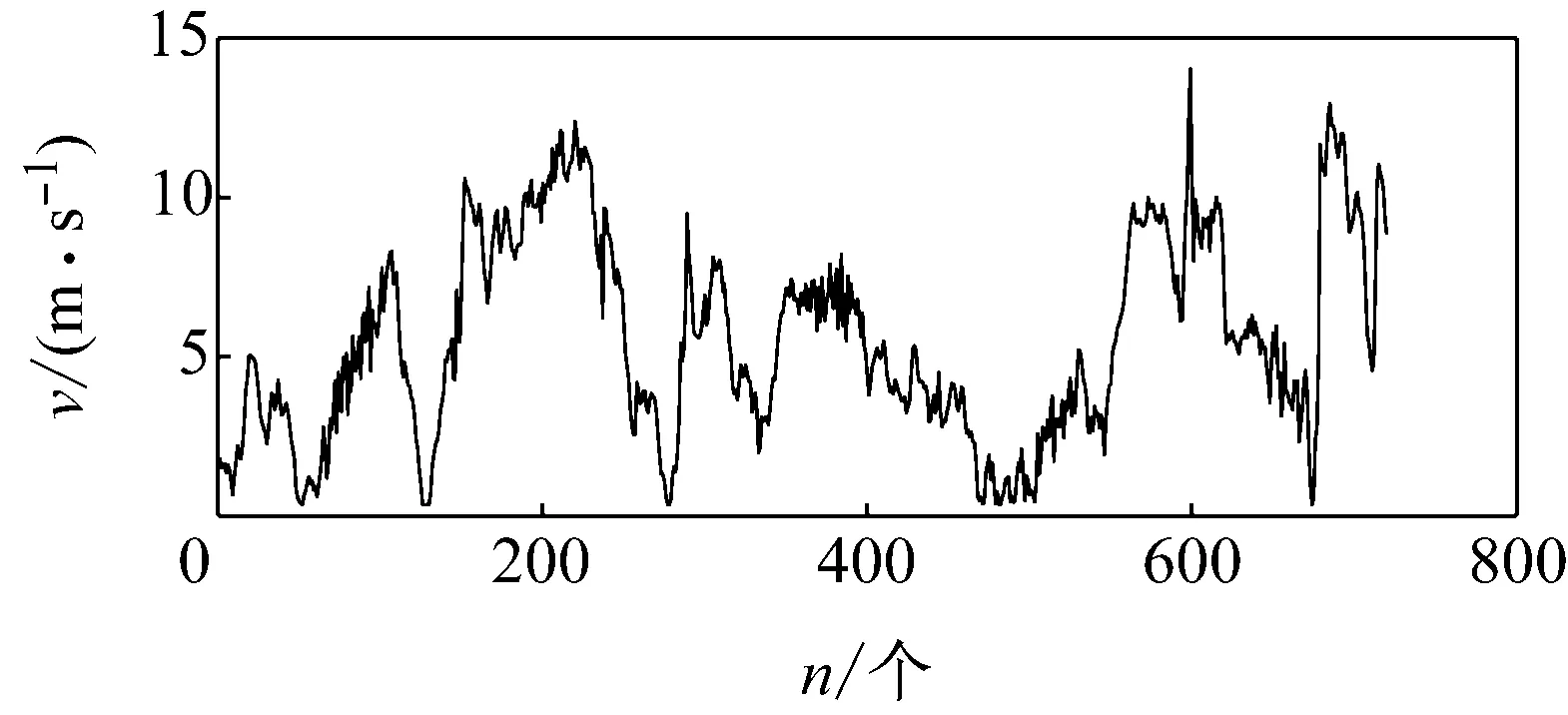
圖5 風速歷史數據圖

選取前576個數據作為訓練集D1，利用ELM模型進行數據訓練；將中間132個數據作為測試集D2，進行風速預測，圖6所示為預測值與實際值。

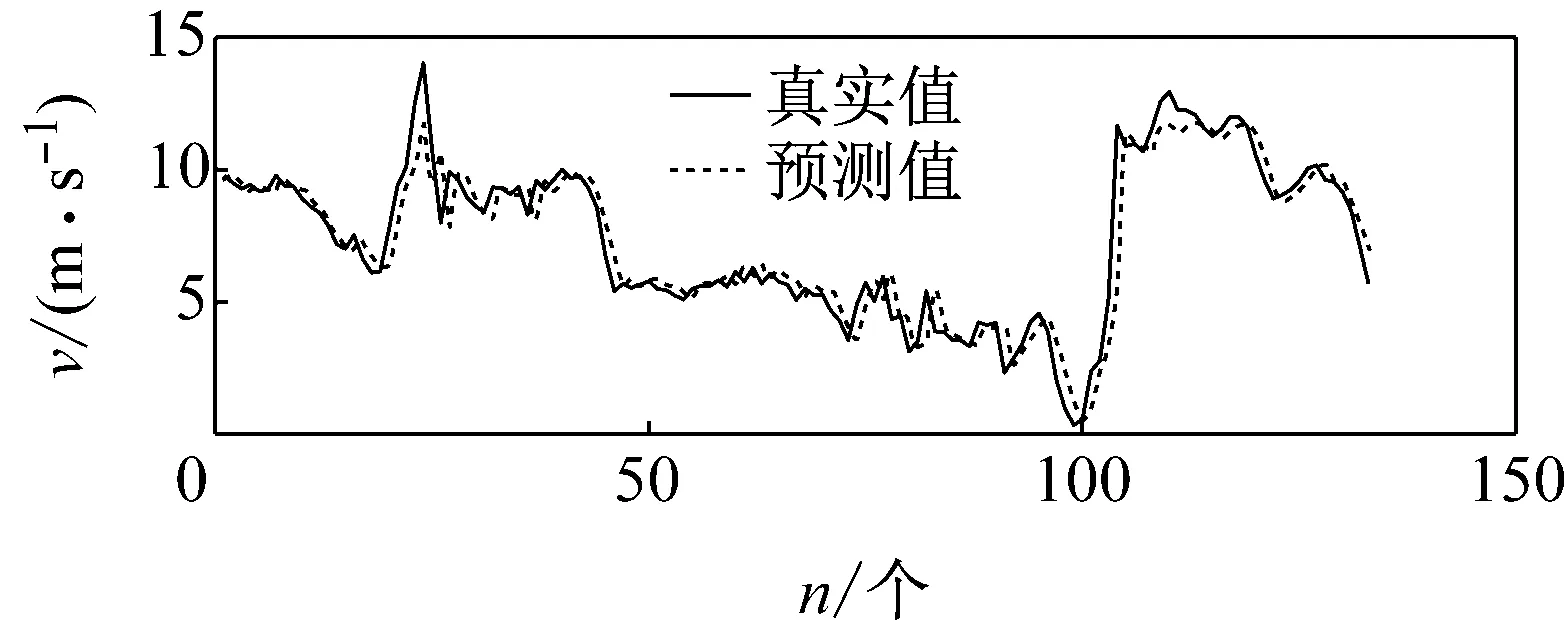
圖6 測試集預測值與實際值

由圖可見，當風速v出現明顯的起伏波動時，風速的預測誤差也越大。

為進一步提高預測精度，本文采用誤差修正方法，利用ADF對誤差數據進行平穩性檢驗。得到如表1所示的1階差分后的單位根檢驗結果。

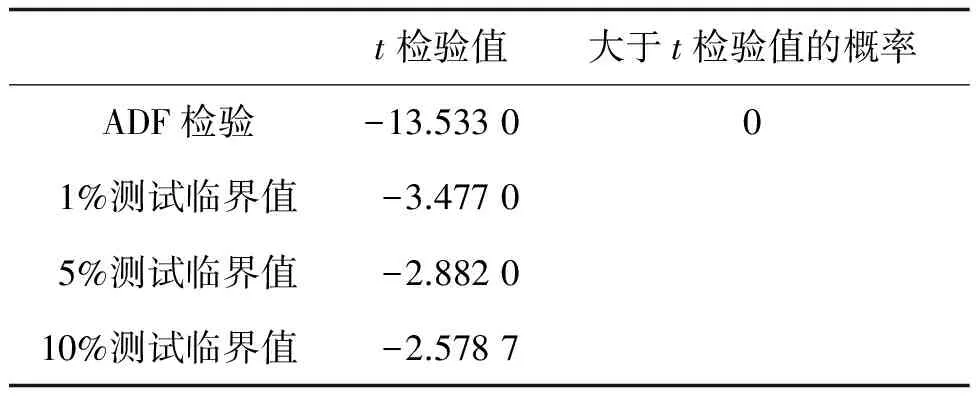
表1 1階差分后單位根檢驗結果

一般認為當ADF檢驗所得到的t檢驗值<5%測試臨界值的t檢驗值時，數據平穩。由表可見，經ADF檢驗的t檢驗值<1%測試臨界值的t檢驗值，故認為1階差分后的誤差數據不存在單位根，此時序列是平穩的。

利用Eviews軟件得到自相關和偏相關圖如圖7所示。圖中，虛線內區域為置信區間。Autocorrelation為自相關圖;Partial Correlation為偏相關圖;AC為自相關系數;PAC為偏相關系數;Q-Stat為Q統計量，用于檢驗白噪聲;Prob為小于顯著性水平的概率。由圖可見，自相關部分，第7個數據已經明顯收束到區間內；而偏相關部分，第2個數據已經明顯收縮在區間內。故依據定階規則，p、q的取值應為 [0-7]內的整數。

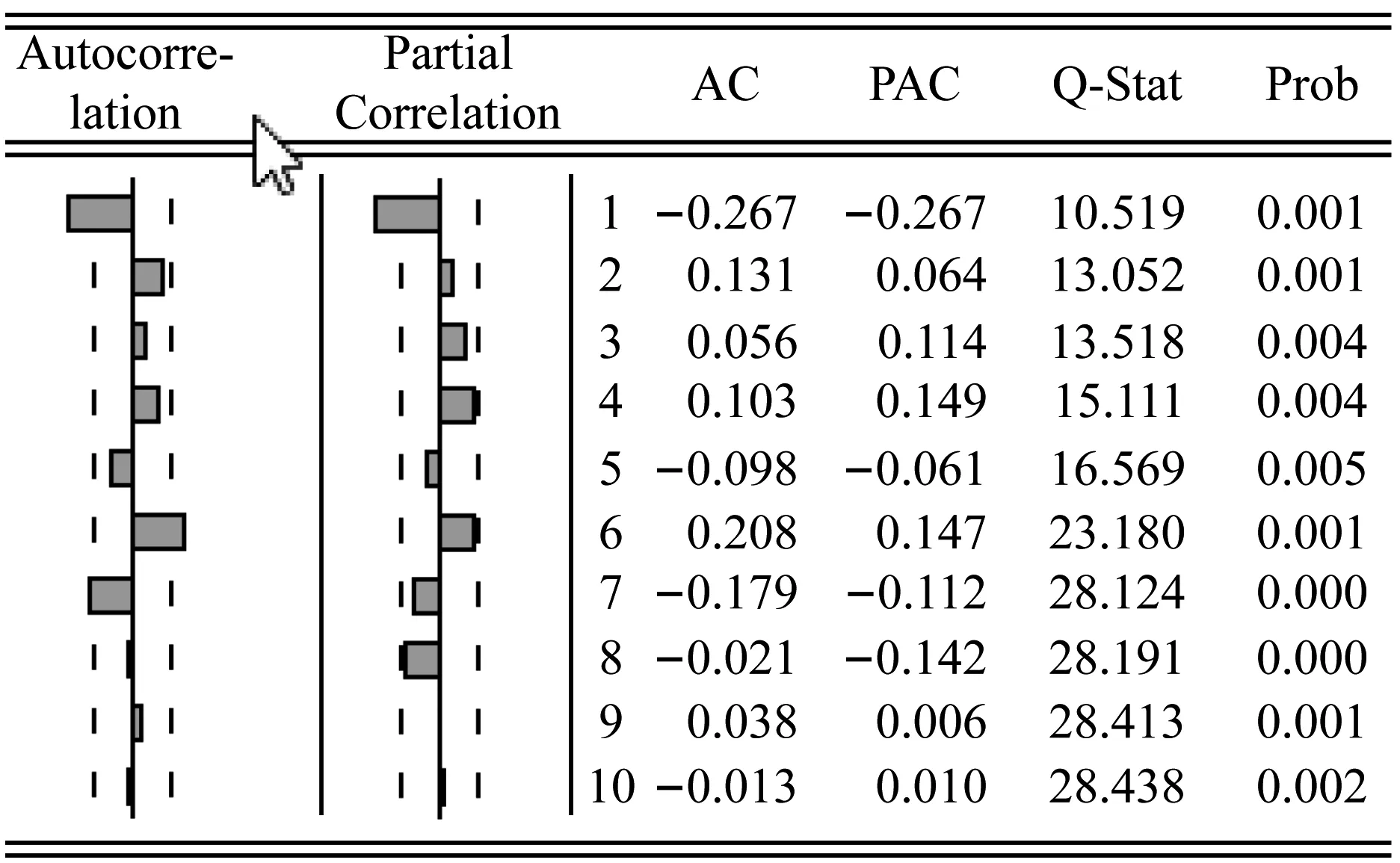
圖7 自相關與偏相關圖

針對(p，q)的不同組合，采用最小二乘法對ARMA(p，q)模型中的未知參數進行估計；然后利用AIC準則,選擇最小的那一組作為ARMA的p，q階數。本文最終選取ARIMA(4，1，2)模型對初步誤差進行預測。

利用ARIMA模型可得到誤差預測結果與實際誤差值的比較，如圖8所示。

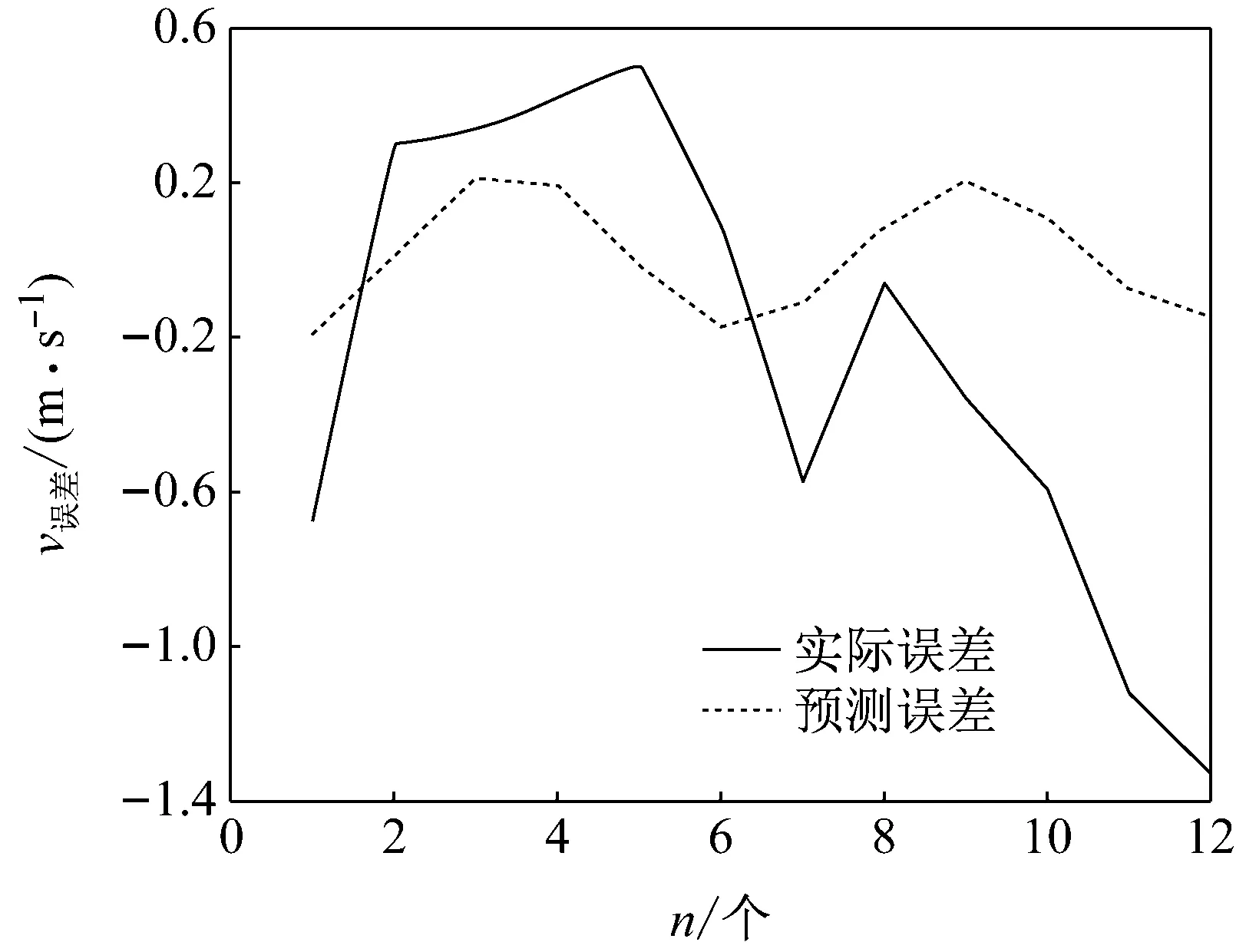
圖8 ARIMA的誤差預測值與實際誤差值的比較

由圖可見，隨著預測步長的增加，誤差的預測值與實際誤差值的偏差加大。因此，ARIMA模型更適用于超短期和短期預測。故將本文方法用于超短期風速的預測，并與ELM預測值、實際值進行比較，圖9所示為超短期預測結果。

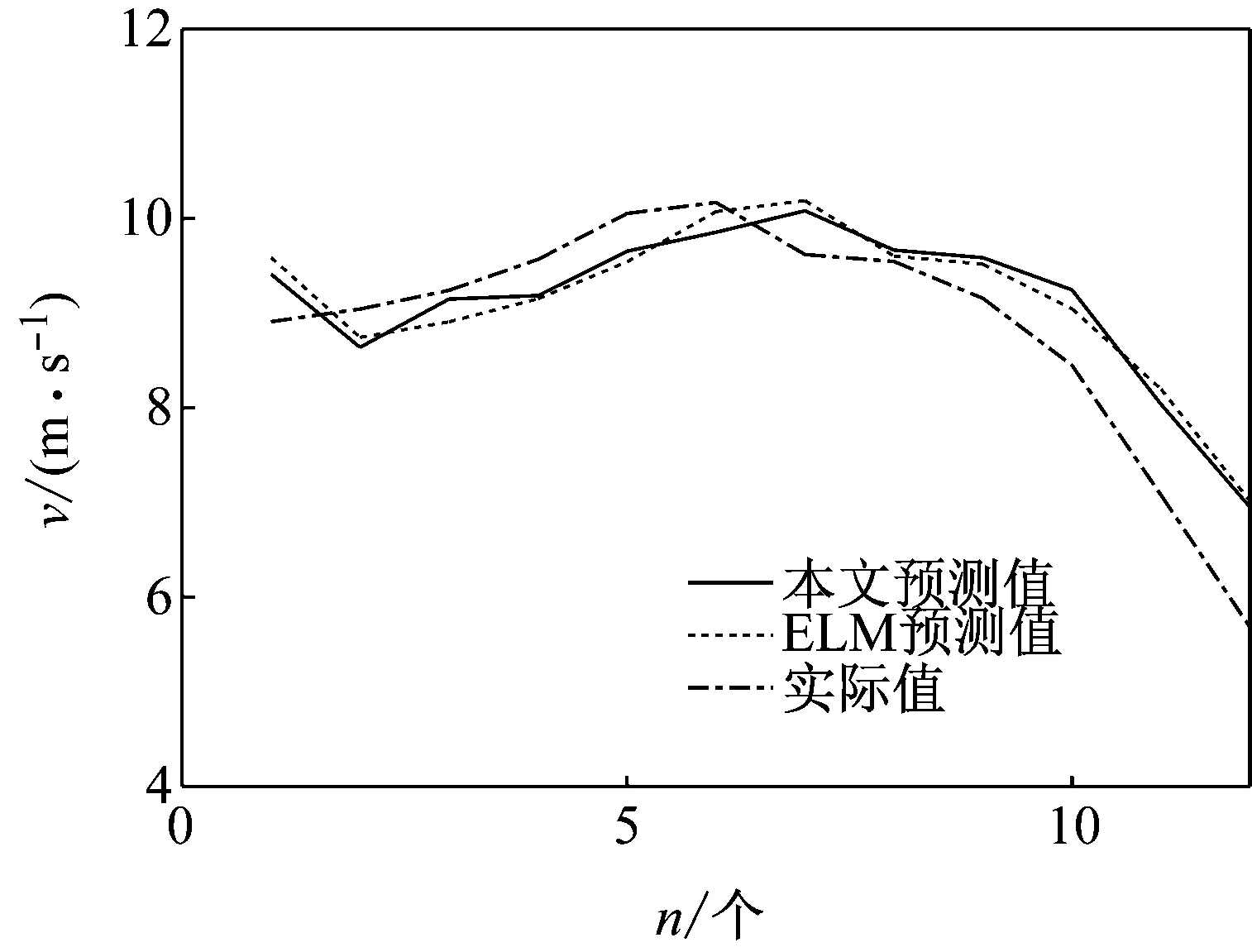
圖9 最終預測圖

由圖可見，應用本文方法進行超短期風速預測，步長越短，預測效果越好。

為評價本文方法的預測精度，選取平均絕對百分比誤差(Mean Absolute Percent Error，MAPE)、平均絕對誤差(Mean Absolute Error，MAE)、均方誤差(Mean Square Error,MSE)來對模型的預測結果的準確度進行評價，其中，

(8)

(9)

(10)

表2給出了本文方法與SVM、LS-SVM、ELM方法的實驗結果評價。

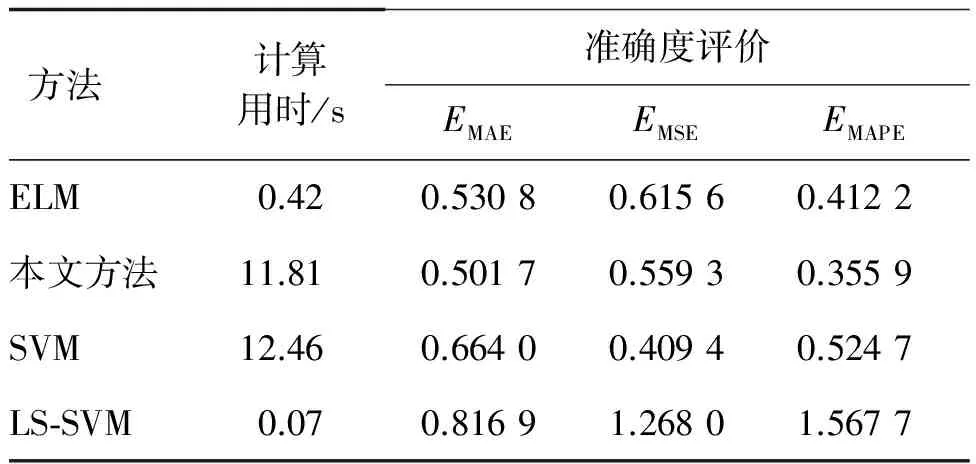
表2 不同模型的風速預測用時與評價結果

由表可見，本文方法的誤差率明顯較LS-SVM和ELM方法低；與SVM 方法相比，除EMSE外，其他指標也明顯低于SVM方法。可見，本文方法有效提高了預測的精度。同時，與SVM相比，本文方法運算速度快，且精度較高，SVM的EMSE值優于本文方法是由于隨機確定的ELM參數不能很好地擬合預測數據中的突變點，這也是本文后續將要進行的研究；LS-SVM計算速度快，但精度較低。因此，本文方法在實際應用中具有一定的優勢。

5 結 語

本文針對具有較大隨機波動性的風速，提出了基于誤差修正的風速超短期預測方法。利用ELM對風速進行初步預測，并取得預測誤差；然后，對誤差進行擬合與預測；最后，對風速初步預測值進行補正，從而求得最終預測值。仿真實驗表明，本文所提出的對誤差進行修正的風速超短期預測方法可以提高風速的預測精度，優于單獨使用ELM前饋神經網絡的預測值。本文所提出的方法也可以推廣到負荷預測等領域，具有一定的泛化能力。

[1] 韓爽. 風電場功率短期預測方法研究 [D]. 北京：華北電力大學, 2008：緒論1-2.

[2] 楊秀媛，肖洋，陳樹勇. 風電場風速和發電功率預測研究 [J]. 中國電機工程學報, 2005, 25(11): 1-5.

[3] 南曉強, 風電預測技術及其運行分析 [D]. 成都：西南交通大學， 2013:5.

[4] 丁藤，馮冬涵，林曉凡，等. 基于修正后ARIMA-GARCH模型的超短期風速預測 [J]. 電網技術, 2017，41(6): 1808-1814.

[5] 孫春順，王耀南，李欣然. 小時風速的向量自回歸模型及應用 [J]. 中國電機工程學報, 2008, 28(14): 112-117.

[6] KARINIOTAKIS G N, STAVRAKAKIS G S, NOGARET E F. Wind power forecasting using advanced neural networks models [J].IEEE Transactions on Energy Conversion,1996,11(4): 762-767.

[7] 張國強，張伯明. 基于組合預測的風電場風速及風電機功率預測 [J]. 電力系統自動化, 2009, 33(18): 92-95，109.

[8] PAPAEFTHYMIOU G, KLOCKL B. MCMC for wind power simulation [J]. IEEE Transactions on Energy Conversion, 2008，23(1): 234-240.

[9] 丁明，張立軍，吳義純. 基于時間序列分析的風電場風速預測模型 [J]. 電力自動化設備, 2005, 25(8): 32-34.

[10] 蔡凱，譚倫農，李春林，等. 時間序列與神經網絡法相結合的短期風速預測 [J]. 電網技術, 2008, 32(8): 82-85，90.

[11] 田中大, 李樹江，王艷文，等. 基于小波變換的風電場短期風速組合預測 [J]. 電工技術學報, 2015，30(9): 112-120.

[12] 薛禹勝，郁琛，趙俊華，等. 關于短期及超短期風電功率預測的評述[J]. 電力系統自動化, 2015,39(6): 141-150.

[13] ZHANG Y, WANG P, NI T, et al. Wind power prediction based on LS-SVM model with error correction [J]. Advances In Electrical and Computer Engineering, 2017, 17(1): 3-8.

[14] PENG Xiaosheng, DENG Diyuan, WEN Jinyu, et al. A very short term wind power forecasting approach based on numerical weather prediction and error correction method [C]//2016 China International Conference on Electricity Distribution. Xi’an, China: IEEE, 2016:1-5.

[15] 王新迎，韓敏. 基于極端學習機的多變量混沌時間序列預測 [J]. 物理學報, 2012,61(8): 97-105.

[16] 張學清，梁軍，張熙，等. 基于樣本熵和極端學習機的超短期風電功率組合預測模型 [J]. 中國電機工程學報, 2013, 33(25): 33-40.

[17] 王輝, 劉達, 王繼龍. 基于譜聚類和優化極端學習機的超短期風速預測 [J]. 電網技術, 2015,39(5): 1307-1314.

[18] 蔣金良，林廣明. 基于ARIMA模型的自動站風速預測 [J]. 控制理論與應用, 2008, 25(2): 374-376.

[19] 房林, 鄒衛星. 多種單位根檢驗法的比較研究 [J]. 數量經濟技術經濟研究, 2007, 24(1): 151-160.

Ultra-short Term Wind Speed Prediction for Extreme Learning Machine Based on Error Correction

PANYilong,DINGYunfei

(School of Electrical Engineering, Shanghai Dianji University, Shanghai 201306, China)

Ultra-short term wind speed prediction is important for the establishment and operation of a wind power forecasting system. Aimed at wind speed with evident fluctuation property and randomness, an ultra-short-term wind speed prediction method for extreme learning machine (ELM) based on error correction is proposed. ELM are used to predict wind speed preliminarily. With the error as original data, using auto-regressive integrated moving average to predict the error. Finally, prediction error is used to correction the wind speed to forecast the wind speed. Simulation results show feasibility and effectiveness of the method in ultra-short term prediction of wind speed.

wind speed prediction; error correction; extreme learning machine (ELM); auto-regressive integrated moving average (ARIMA)

2017 -09 -10

國家自然科學基金項目資助(11302123)；上海市浦江人才計劃資助(15PJ1402500)；上海市教育委員會科研創新項目資助(14YZ163)；上海市教育委員會和上海市教育發展基金會"晨光計劃"資助(13CG63)

潘羿龍(1992-)，男，碩士生，主要研究方向為模式識別與智能系統，E-mail：363889821@qq.com

丁云飛(1976-)，女，教授，博士，主要研究方向為模式識別、智能控制、故障診斷、人工智能、數據挖掘，E-mail：dingyf@sdju.edu.cn

2095 - 0020(2017)06 -0342 - 06

TM 614； TP 183

A