空間太陽能電站重力姿態-軌道-結構耦合特性
劉玉亮,鄔樹楠,劉家夫,吳志剛,
1.大連理工大學 航空航天學院,大連 116024 2.大連理工大學 工業裝備結構分析國家重點實驗室,大連 116024 3.沈陽航空航天大學 航空航天工程學部,沈陽 110136
空間太陽能電站重力姿態-軌道-結構耦合特性
劉玉亮1,2,鄔樹楠1,2,劉家夫3,吳志剛1,2,*
1.大連理工大學 航空航天學院,大連 116024 2.大連理工大學 工業裝備結構分析國家重點實驗室,大連 116024 3.沈陽航空航天大學 航空航天工程學部,沈陽 110136
基于結構小變形假設,將太陽帆塔式空間太陽能電站(SSPS)簡化為兩端自由的Euler-Bernoulli梁模型,并建立在重力作用下,假設只考慮軌道平面內電站的姿態和軌道運動與結構振動的耦合動力學方程。其受到的重力、重力梯度力矩和廣義重力將以其結構尺寸與運行軌道半徑的比值為變量進行泰勒展開,并保留至四階項。通過對其動力學方程的分析發現,當假設只考慮軌道平面內的姿態運動和軌道平面內結構的橫向振動時,結構振動對姿態和軌道運動的影響只存在于三階及其以上的重力和重力梯度力矩中。此外,在重力激勵下當電站的結構角頻率小于某一特定值時,其結構振動將會出現屈曲不穩定的現象。保證電站結構振動穩定的條件也將在文中給出。為了分析重力激勵對結構振動的影響,提出了“等效角頻率”的概念。數值仿真表明,當電站結構角頻率較低時,重力激勵將對電站的振動產生很大影響。而且重力引起的姿態-軌道-結構的耦合作用也將對空間太陽能電站的軌道運動產生較大影響,軌道半徑誤差能達千米量級。
空間太陽能電站;姿態-軌道耦合;結構振動;重力梯度;泰勒展開
空間太陽能電站(SSPS)的概念由美國科學家Glaser博士于1968年提出[1]。自從這一概念提出以來,多個航天大國陸續開展了相關研究,并提出了多種概念設計,如美國國家航空航天局的“ALPHA”構型[2],日本宇航開發局的繩系構型[3],歐洲太空局的太陽帆塔式構型[4],以及中國空間技術研究院侯欣賓等提出的多旋轉關節式構型[5]和西安電子科技大學段寶巖院士等提出的“OMEGA”式構型[6]。迄今為止,世界各國一共提出了20多種SSPS方案[7]。
在目前關于SSPS的研究中,大都集中在對概念設計的研究,而對其在軌運行過程中的軌道、姿態與結構動力學行為的研究較少。為保證SSPS的正常工作,首先需要清楚地了解其在軌動力學行為。Graf, Jr[8]首先分析了SSPS運行在地球靜止軌道上的軌道動力學特性。McNally等[9]提出了一種新穎的SSPS運行軌道——地球同步拉普拉斯軌道,并指出了這種軌道相對于地球靜止軌道的優勢。劉玉亮等[10]對該種軌道的動力學特性進行了進一步的分析,提出了評價SSPS軌道的指標。McNally等[11]進一步研究了運行在地球同步拉普拉斯軌道的SSPS在無控狀態下的姿態運動。Wie和Roithmayr[12]初步分析了地球靜止軌道“Abacus”式SSPS的軌道和姿態運動特性,并設計了軌道保持控制器和對日指向控制器。Ishimura等[13-14]通過建立起繩系SSPS的有限元模型,綜合分析了在地球引力場中其軌道運動、姿態運動及結構振動的穩定性問題。Glaese和McDonald[15]基于多體動力學的理論建立了“ISC”式SSPS的軌道和姿態運動及結構振動的動力學模型,并設計了太陽指向控制器。周荻和范繼祥[16]針對繩系SSPS大角度機動時產生的振動問題進行了研究,提出了一種主動振動控制系統。魏乙等[17]通過采用絕對節點坐標法建立起了繩系SSPS在軌運行中軌道、姿態和結構振動的耦合動力學方程,并對其動力學特性進行了分析。
在上述關于SSPS姿態和軌道運動和結構振動的研究中,大都沒考慮三者之間的相互耦合作用[8-12,15,17];其軌道運動常被假設為開普勒軌道,而姿態運動和結構振動與軌道運動之間的耦合作用常忽略不計。傳統衛星因具有較小尺寸和較高結構頻率的特點,這種假設是合理的。但對于空間太陽能電站這種超大、超柔的空間結構而言,它們之間的耦合作用需要重新考慮。此外,有學者采用有限元方法綜合分析了SSPS軌道、姿態和結構振動的動力學特性,但并沒有揭示它們之間的耦合機理[13-14,16]。
目前,在關于航天器姿態運動和軌道運動耦合作用的研究中,很多學者已取得了一些優異的成果。Duboshin[18]首先推導了兩個任意形狀天體在相互引力作用下的姿態和軌道耦合運動的微分方程。Lange[19]研究了一種任意構型的航天器在地球引力場中的姿態和軌道耦合運動,并將其所受到的重力和重力梯度力矩通過Taylor級數進行展開,保留至ε2項(ε=ρ/R,ρ為航天器的特征尺寸,R為航天器的運行軌道半徑),為姿態和軌道耦合運動的數值運算提供了一種方法。Sincarsin和Hughes[20]研究了一種超大型的板狀航天器在地球引力場中的姿態和軌道耦合運動,并將其所受到的重力和重力梯度力矩保留至ε4項。Ashenberg[21]研究了兩個任意形狀且相互吸引的天體之間的姿態和軌道耦合問題,并提出了高階慣性積的概念。通過采用Ashenberg提出的方法,Wang和Xu[22]分析了一種特殊構型的航天器在某一小行星表面運動時的姿態和軌道耦合特性。基于上述研究成果,劉玉亮等[23-24]研究了太陽帆塔式SSPS在地球引力場中的姿態和軌道耦合問題。然而,在這些研究中,大都將航天器或者天體當成剛體來處理,并未考慮柔性振動所帶來的影響。對于SSPS這種超柔的航天器而言,這種假設是不合理的,因此需要重新考慮柔性振動給SSPS姿態和軌道耦合運動帶來的影響。
為了解決上述問題,本文將重點研究太陽帆塔式空間太陽能電站(見圖1)在地球引力場作用下的姿態-軌道-結構耦合作用,并揭示它們之間的耦合機理。全文安排如下:第1節,將對坐標系和符號進行定義并推導出SSPS在軌運行過程中的軌道運動、姿態運動和結構振動的動力學方程。第2節,將SSPS受到的重力、重力梯度力矩和廣義重力進行泰勒展開,并保留至四階項,同時對其動力學方程進行分析,給出“等效角頻率”的定義。第3節,通過數值仿真對姿態-軌道-結構耦合的動力學特性進行分析。結論將在第4節給出。
圖1 太陽帆塔式空間太陽能電站
Fig.1 Sun tower space solar power station
1 動力學方程
1.1 坐標系與假設
為了便于描述SSPS的運動,本節將給出坐標系和一些符號的定義,如圖2和圖3所示。由于太陽帆塔式SSPS的寬度h遠小于其長度l,如圖1所示,故在本文中,太陽帆塔式SSPS被簡化成一個兩端自由的Euler-Bernoulli梁模型[24],SSPS的結構振動假設只考慮垂直于太陽能電池板表面方向的橫向振動,且假設只考慮SSPS軌道平面內的姿態運動和結構振動,即垂直于太陽能電池板表面方向的結構橫向振動在SSPS的軌道平面內。

圖2 坐標系示意圖
Fig.2 Schematic of coordinate systems
圖3 太陽帆塔式SSPS在軌示意圖
Fig.3 Schematic of sun tower SSPS in the Earth’s orbit
1.2 動力學方程
在本文中,SSPS的變形被假設為小變形,可通過模態坐標表示,則u可表示為
(1)
式中:Ai(t)為第i階模態的模態坐標;φi(x)為第i階歸一化的模態振型,且滿足式(2)所示條件[26]。
(2a)
(2b)
(2c)
式中:δij為Kronecker符號;Mii為第i階模態的廣義質量,對于歸一化的振型φi(x),Mii≡1 kg。
單位質量dm相對于慣性系Oei1j1的絕對加速度在浮動坐標系Oi2j2下的分量可表示為
ω×(ω×ρb)]dm=L(qb)+fgdm
(3a)
dm=σdx
(3b)
沿SSPS的長度方向對式(3a)進行積分,并結合式(2a)和式(3b)對方程進行化簡,可得到SSPS的軌道運動方程為
(4)
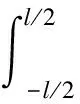
(5)

(6)
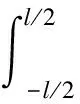
(7)
2 重力、重力梯度力矩和廣義重力
為便于進行數值計算,需要得到式(4)、式(5)和式(7)右端項的顯式表達式。在本節中,將會對SSPS在軌運行過程中受到的重力、重力梯度力矩及廣義重力進行推導。
在本文中,地球被假設成一個均勻的球體,不考慮地球扁率帶來的影響,則SSPS單位質量受到的重力可表示為
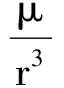
(8)
式中:μ為地球引力常數;r=rb,且可表示為
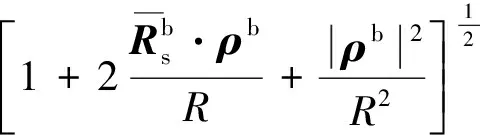
(9)
將式(9)通過泰勒級數進行展開,保留至(ρb/R)4,并將其代入式(8)可得
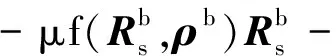
(10a)
(10b)
(10c)
(11)
式中:i≠j且I1=Jxx。由式(2a)、式(2b)、式(2c)和O作為SSPS的質心可知,式(12)所示條件得以滿足。
Jx=Jxxx=Jφi=Jx φi=Jφiφj=0
(12)
此外,對于兩端自由的Euler-Bernoulli梁而言,其橫向振動的各階歸一化振型可表示為
(13)

Jxxφe=Jxφoφo=Jxφeφe=Jxxxφo=
Jxxφeφo=Jxxxxφe=Jxxxφoφo=Jxxxφeφe=0
(14)
從附錄中式(A1)~式(A3)可以看出,當假設只考慮軌道平面內的姿態運動和結構振動時,且結構振動假設只考慮垂直于太陽能電池板表面方向的橫向振動,太陽帆塔式SSPS的結構振動對其受到的重力和重力梯度力矩的影響存在于三階及其以上的重力和重力梯度力矩中,對低階重力和重力梯度力矩則無影響。此外,不同的姿態角下,SSPS受到的二階及其以上的重力和一階及其以上的廣義重力的大小不同;而且,在不同的軌道半徑下,SSPS受到的各階重力梯度力矩和廣義重力的大小也不同,故SSPS的軌道運動、姿態運動和結構振動之間存在著耦合關系。
將式(A3)代入式(7),并結合式(14)可得
(15)
(16)
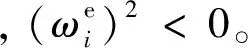
(17)

(18)
(19)
3 仿真與分析
為了分析SSPS在軌運行中,其結構的“等效角頻率”隨姿態角的變化規律和各階重力、重力梯度力矩及廣義重力對其軌道運動、姿態運動和結構振動的影響。本節將給出兩個數值仿真算例。


圖4 一階臨界角頻率的平方隨θ的變化 Fig.4 Variation of squared value of the first ordercritical angular frequency ()2 with θ
圖5 不同一階角頻率下F隨θ的變化
Fig.5Charts of F change over θ with different first order angular frequencies
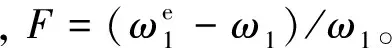
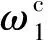
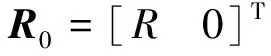
表1給出了采用不同模型計算時所考慮的重力、重力梯度力矩及廣義重力。
表1不同階次模型的重力、重力梯度力矩和廣義重力
Table1Gravitationalforces,torquesandgeneralizedforcesofdifferentordermodels
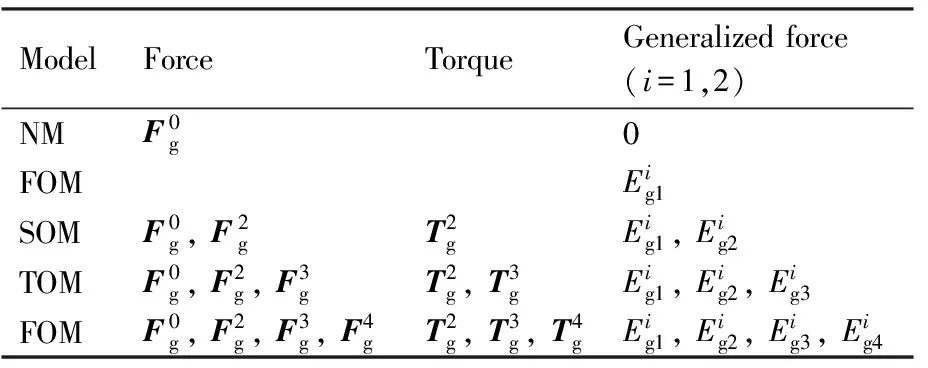
ModelForceTorqueGeneralizedforce(i=1,2)NMF0g0FOMEig1SOMF0g,F2gT2gEig1,Eig2TOMF0g,F2g,F3gT2g,T3gEig1,Eig2,Eig3FOMF0g,F2g,F3g,F4gT2g,T3g,T4gEig1,Eig2,Eig3,Eig4
Notes:NM——None higher orders Model; FOM, SOM, TOM, and FOM represent the First, Second, Third, and Fourth order Models, respectively
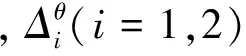
圖6 不同階次的重力對軌道運動的影響
Fig.6 Influences of different order gravitational forces on orbital motion
圖7 不同階次的重力梯度力矩對姿態運動的影響
Fig.7 Influences of different order gravitational gradient torques on attitude motion
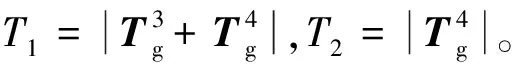
圖8 不同階次的廣義重力對結構振動的影響
Fig.8 Influences of different order generalized gravitational forces on structural vibration
4 結 論
1) 對于假設只考慮軌道平面內的姿態運動和軌道平面內結構橫向振動的兩端自由的梁式空間太陽能電站,其結構振動對姿軌運動的影響只存在于三階及其以上的重力和重力梯度力矩中,其影響可忽略不計。
2) 在一定姿態角和重力激勵下,當空間太陽能電站的結構角頻率低于某一值時,其結構將出現屈曲不穩定,其主要原因是由于結構因形變產生的回復力小于結構受到的重力梯度力引起的。此外,當結構的角頻率靠近臨界角頻率時,重力激勵將對其結構振動產生較大影響,且主要由前兩階廣義重力引起。
3) 空間太陽能電站的姿態-軌道-結構耦合作用將對電站的軌道運動產生較大影響,能使其軌道半徑誤差達至千米量級,且主要由二階重力引起。此外,對其姿態運動也將產生一定影響,姿態角誤差將隨時間逐漸積累。
[1] GLASER P E. Power from the sun: Its future[J]. Science, 1968, 162(3856): 857-861.
[2] MANKINS J, KAYA N, VASILE M. SPS-ALPHA: The first practical solar power satellite via arbitrarily large phased array: AIAA-2012-3978[R]. Reston, VA: AIAA, 2012.
[3] SASAKI S, TANAKA K, HIGUCHI K, et al. A new concept of solar power satellite: Tethered-SPS[J]. Acta Astronautica, 2007, 60(3): 153-165.
[4] SEBOLDT W, KLIMKE M, LEIPOLD M, et al. European sail tower SPS concept[J]. Acta Astronautica, 2001, 48(5): 785-792.
[5] 侯欣賓, 王立, 張興華, 等. 多旋轉關節空間太陽能電站概念方案設計[J]. 宇航學報, 2015, 36(11): 1332-1338.
HOU X B, WANG L, ZHANG X H, et al. Concept design on multi-rotary joints SPS[J]. Journal of Astronautics, 2015, 36(11): 1332-1338 (in Chinese).
[6] YANG Y, ZHANG Y Q, DUAN B Y, et al. A novel design project for space solar power station (SSPS-OMEGA)[J]. Acta Astronautica, 2016, 121: 51-58.
[7] 王立, 侯欣賓. 空間太陽能電站的關鍵技術及發展建議[J]. 航天器環境工程, 2014, 31(4): 343-350.
WANG L, HOU X B. Key technologies and some suggestions for the development of space solar power station[J]. Spacecraft Environment Engineering, 2014, 31(4): 343-350 (in Chinese).
[8] GRAF O F, Jr. Orbital motion of the solar power satellite: NASA-CP-151603[R]. Washington, D.C.: NASA, 1978.
[9] MCNALLY I, SCHEERES D, RADICE G. Locating large solar power satellites in the geosynchronous Laplace plane[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(3): 489-505.
[10] 劉玉亮, 鄔樹楠, 吳志剛, 等. 空間太陽能電站地球同步拉普拉斯軌道動力學特性[J]. 中國空間科學技術, 2016, 36(5): 1-8.
LIU Y L, WU S N, WU Z G, et al. Dynamic characteristics of geosynchronous Laplace orbit for space solar power station[J]. Chinese Space Science and Technology, 2016, 36(5): 1-8 (in Chinese).
[11] MCNALLY I, SCHEERES D, RADICE G. Attitude dynamics of large geosynchronous solar power satellites[C]∥AIAA/AAS Astrodynamics Specialist Conference. Reston, VA: AIAA, 2014: 1-13.
[12] WIE B, ROITHMAYR C M. Attitude and orbit control of a very large geostationary solar power satellite[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(3): 439-451.
[13] ISHIMURA K, NATORI M, WADA M. Stability analysis and decentralized system design of large space structures based on potential field[C]∥13th International Conferenc on Adaptive Structures and Technologies. Boca Raton, FL: CRC Press, 2003: 413-422.
[14] ISHIMURA K, HIGUCHI K. Coupling between structural deformation and attitude motion of large planar space structures suspended by multi-tethers[J]. Acta Astronautica, 2007, 60(8): 691-710.
[15] GLAESE J R, MCDONALD E J. Space solar power multi-body dynamics and controls, concepts for the integrated symmetrical concentrator configuration: TCD20000222A[R]. Washington, D.C.: NASA, 2000.
[16] 周荻, 范繼祥. 繩系太陽能發電衛星姿態機動的主動振動控制[J]. 宇航學報, 2012, 33(5): 605-611.
ZHOU D, FAN J X. Boundary control in the attitude maneuvering of tethered space solar power satellite[J]. Journal of Astronautics, 2012, 33(5): 605-611 (in Chinese).
[17] 魏乙, 鄧子辰, 李慶軍, 等. 繩系空間太陽能電站動力學響應分析[J]. 宇航學報, 2016, 37(9): 1041-1048.
WEI Y, DENG Z C, LI Q J, et al. Analysis of dynamic response of tethered space solar power station[J]. Journal of Astronautics, 2016, 37(9): 1041-1048 (in Chinese).
[18] DUBOSHIN G N. The differential equations of translational-rotational motion of mutally attracting rigid bodies[J]. Soviet Astronomy, 1958, 2: 239-250.
[19] LANGE B. Linear coupling between orbital and attitude motions of a rigid body[J]. Journal of the Astronautical Sciences, 1970, 18: 150-167.
[20] SINCARSIN G B, HUGHES P C. Gravitational orbit-attitude coupling for very large spacecraft[J]. Celestial Mechanics, 1983, 31(2): 143-161.
[21] ASHENBERG J. Mutual gravitational potential and torque of solid bodies via inertia integrals[J]. Celestial Mechanics and Dynamical Astronomy, 2007, 99(2): 149-159.
[22] WANG Y, XU S. Gravitational orbit-rotation coupling of a rigid satellite around a spheroid planet[J]. Journal of Aerospace Engineering, 2012, 27(1): 140-150.
[23] 吳志剛, 劉玉亮, 張開明, 等. 高階重力和力矩對空間太陽能電站運動的影響[J]. 空間控制技術與應用, 2016, 42(4): 1-5.
WU Z G, LIU Y L, ZHANG K M, et al. The influences of higher order gravitational force and torque to the motion of space solar power station[J]. Aerospace Control and Application, 2016, 42(4): 1-5 (in Chinese).
[24] LIU Y L, WU S N, ZHANG K G, et al. Gravitational orbit-attitude coupling dynamics of a large solar power satellite[J]. Aerospace Science and Technology, 2017, 62: 46-54.
[25] 劉暾, 趙鈞. 空間飛行器動力學[M]. 哈爾濱: 哈爾濱工業大學出版社, 2003: 153-154.
LIU D, ZHAO J. Dynamics of spacecraft[M]. Harbin: Harbin Institute of Technology Press, 2003: 153-154 (in Chinese).
[26] ASHLEY H. Observations on the dynamic behavior of large flexible bodies in orbit[J]. AIAA Journal, 1967, 5(3): 460-469.
[27] BAINUM P M, KUMAR V K, JAMES P K. The dynamics and control of large flexible space structures, Part B: Development of continuum model and computer simulation: NASA-CR-l63612[R]. Washington,D.C.: NASA, 1978.
[28] KANE T R, RYAN R, BANERJEE A K. Dynamics of a cantilever beam attached to a moving base[J]. Journal of Guidance, Control, and Dynamics, 1987, 10(2): 139-151.
[29] 楊輝, 洪嘉振, 余征躍. 兩種剛柔耦合動力學模型的對比研究[J]. 上海交通大學學報, 2002, 36(11): 1591-1595.
YANG H, HONG J Z, YU Z Y. Study on two dynamic models for a rigid-flexible coupling system[J]. Journal of Shanghai Jiaotong University, 2002, 36(11): 1591-1595 (in Chinese).
[30] ASHLEY H. Observations on the dynamic behavior of large flexible bodies in orbit[J]. AIAA Journal, 1967, 5(3): 460-469.
附錄A
(A1)
式中:
(A2)
式中:
(A3)
其中:
其中:
(A4)
Gravitationalattitude-orbit-structurecouplingofspacesolarpowerstation
LIUYuliang1, 2,WUShu’nan1, 2,LIUJiafu3,WUZhigang1, 2, *
1.SchoolofAeronauticsandAstronautics,DalianUniversityofTechnology,Dalian116024,China2.StateKeyLaboratoryofStructuralAnalysisforIndustrialEquipment,DalianUniversityofTechnology,Dalian116024,China3.DepartmentofAerospaceEngineering,ShenyangAerospaceUniversity,Shenyang110136,China
Basedontheassumptionofsmalldeformationofthestructure,thesuntowerSpaceSolarPowerStation(SSPS)issimplifiedtoaEuler-Bernoullibeamwithbothendsbeingfree,andthecoupleddynamicalequationsfortheorbitalandattitudemotionsandstructurevibrationofthestationundertheexcitationofgravitationalforceareproposed,whichconsideronlytheattitudemotionandthestructurevibrationontheorbitalplane.Thegravitationalforce,torqueandgeneralizedforceareexpandedinaTaylorseriesinthesmallratio(spacecraftsize/orbitalradius)whichpermitstermsuptofourthordertoberetained.Ananalysisofthestructuralvibrationequationsfindsthattheinfluenceofstructuralvibrationontheorbitalandattitudemotionexistsonlyinnolessthanthree-ordergravitationalforcesandtorquesifonlyattitudemotionandtransversevibrationofthestructureontheorbitalplaneareconsidered.Inaddition,abucklinginstabilityofthestructurecanoccurundertheexcitationofgravitationalforceiftheangularfrequencyofthespacesolarpowerstationisbelowacertainthreshold.Theconditiontoguaranteethestabilizationofthestructurevibrationisalsoderived.Aconceptof“equivalentangularfrequency”isdefinedforanalyzingtheinfluenceoftheexcitationofgravitationalforceonstructuralvibration.Numericalsimulationsshowthattheinfluenceoftheexcitationofgravitationalforceonthestructuralvibrationisgreatiftheangularfrequencyislow.Thecouplingeffectamongtheorbitalandattitudemotionandstructuralvibrationonorbitalmotionisalsogreat,andtheerroroftheorbitalradiuscanreachtheorderofonekilometer.
spacesolarpowerstation;attitude-orbitcoupling;structuralvibration;gravitygradient;Taylorexpansion
2017-03-15;
2017-04-17;
2017-05-17;Publishedonline2017-12-071001
URL:http://hkxb.buaa.edu.cn/CN/html/20171215.html
s:NationalNaturalScienceFoundationofChina(11432010,11502040);theFundamentalResearchFundsfortheCentralUniversities(DUT15LK31)
.E-mailwuzhg@dlut.edu.cn
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2017.221244
2017-03-15;退修日期2017-04-17;錄用日期2017-05-17;網絡出版時間2017-12-071001
http://hkxb.buaa.edu.cn/CN/html/20171215.html
國家自然科學基金(11432010,1150240); 中央高校基本科研業務費專項資金(DUT15LK31)
.E-mailwuzhg@dlut.edu.cn
劉玉亮,鄔樹楠,劉家夫,等. 空間太陽能電站重力姿態-軌道-結構耦合特性J. 航空學報,2017,38(12):221244.LIUYL,WUSN,LIUJF,etal.Gravitationalattitude-orbit-structurecouplingofspacesolarpowerstationJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):221244.
V412
A
1000-6893(2017)12-221244-12
徐曉)

