基于SDT和間接平差的中機身自動調(diào)姿精度分析

朱永國，張文博，劉春鋒，趙爽

1.南昌航空大學(xué) 航空制造工程學(xué)院，南昌 330063 2.中航工業(yè)江西洪都航空工業(yè)集團有限責(zé)任公司，南昌 330024

基于SDT和間接平差的中機身自動調(diào)姿精度分析

朱永國1,*，張文博1，劉春鋒2，趙爽2

1.南昌航空大學(xué) 航空制造工程學(xué)院，南昌 330063 2.中航工業(yè)江西洪都航空工業(yè)集團有限責(zé)任公司，南昌 330024

以4定位器式中機身調(diào)姿機構(gòu)為研究對象，提出了一種飛機部件動態(tài)調(diào)姿精度的分析方法。首先，使用小位移旋量(Small Displacement Torsors, SDT)對定位器各關(guān)鍵公差建模，建立了定位器4層次誤差SDT模型。其次，基于微分變換推導(dǎo)出定位器制造誤差與中機身位姿誤差之間的顯式函數(shù)關(guān)系，給出了制造誤差傳遞與累積系數(shù)矩陣。在此基礎(chǔ)上，結(jié)合5次多項式軌跡規(guī)劃方法，建立了單個定位器動態(tài)誤差傳遞數(shù)學(xué)模型。然后，針對多定位器的誤差耦合，綜合運用間接平差法和加權(quán)最小二乘法，提出了多定位器球鉸中心點動態(tài)誤差耦合計算方法，并推導(dǎo)出了誤差補償量計算表達式。試驗結(jié)果表明，依據(jù)該方法計算定位器驅(qū)動修正值，對調(diào)姿機構(gòu)實施誤差補償，能較好地降低調(diào)姿誤差，提高調(diào)姿部件的定位精度，為保證大部件對接裝配協(xié)調(diào)準(zhǔn)確度提供了有效途徑。

飛機；裝配；機身；小位移旋量(SDT)；間接平差；誤差傳遞；誤差耦合

依靠經(jīng)緯儀測量，手工操作的傳統(tǒng)飛機大部件對接裝配方法已不能滿足現(xiàn)代飛機高精度、高效、經(jīng)濟性等制造要求。需采用數(shù)字化對接裝配系統(tǒng)，使飛機大部件對接裝配朝著自動化和數(shù)字化的方向發(fā)展[1-3]。飛機大部件數(shù)字化對接裝配系統(tǒng)主要由數(shù)控位置和姿態(tài)(以下簡稱位姿)調(diào)整機構(gòu)、高精度數(shù)字化測量系統(tǒng)、運動控制系統(tǒng)等組成。其中，數(shù)控位姿調(diào)整機構(gòu)往往采用三坐標(biāo)POGO或定位器來實現(xiàn)大部件位姿的精確定位[4-7]。位姿能否精確定位既是大部件對接裝配成功的關(guān)鍵因素，也是影響對接裝配質(zhì)量的重要因素。因此，需明晰調(diào)姿系統(tǒng)的誤差源，建立位姿調(diào)整(以下簡稱調(diào)姿)機構(gòu)的誤差傳遞與累積計算表達式，并在裝配過程實施動態(tài)誤差補償，以提高大部件的定位精度。

目前，已有不少學(xué)者對大部件調(diào)姿精度進行了研究。李晨等運用多體運動學(xué)理論對三坐標(biāo)定位器式調(diào)姿機構(gòu)的誤差進行了分析，采用蒙特卡羅模擬法對誤差分布進行了仿真[8]。郭飛燕等針對滾珠絲杠傳動系統(tǒng)的安裝誤差，建立了柔性工裝立柱單軸運動的定位誤差模型[9]。郭志敏等研究了POGO柱受力變形引起的調(diào)姿誤差[10]。朱永國等利用齊次變換矩陣分析了調(diào)姿機構(gòu)各誤差源與調(diào)姿部件位姿誤差的關(guān)系[11-12]。以上研究成果為大部件調(diào)姿精度分析提供了基礎(chǔ)，但仍存在以下3個亟待完善的方面：① 以往的研究沒有顧及到調(diào)姿機構(gòu)運動對調(diào)姿精度的影響，只進行了靜態(tài)誤差分析；② 以往的研究只關(guān)注于誤差的傳遞與累積，沒有提出驅(qū)動機構(gòu)誤差補償?shù)娘@式計算方法；③ 以往的研究僅分析了單個定位器對部件調(diào)姿精度的影響，沒有給出多個定位器的耦合誤差與調(diào)姿部件位姿誤差之間的顯式函數(shù)關(guān)系，也沒有顧及到定位器球鉸副中心坐標(biāo)誤差與調(diào)姿部件位姿誤差的非線性強耦合關(guān)系。

小位移旋量(SDT)是表示剛體微小位移的6個運動分量所構(gòu)成的矢量，Bourdet等首次將SDT引入到公差領(lǐng)域，并將其成功應(yīng)用于不同類型的公差分析中[13-15]。文獻[16-18]借助SDT對幾何要素的形狀、位置、方向和尺寸誤差進行了定量的描述。工程實際中，調(diào)姿機構(gòu)的制造誤差均相比其幾何尺寸是微小量，且調(diào)姿機構(gòu)剛性大，調(diào)姿過程中受力變形相對于其幾何尺寸也是微小量，因此，可以引入基于剛體假設(shè)的SDT公差建模方法進行調(diào)姿機構(gòu)的誤差分析。

基于以上分析，三坐標(biāo)定位器式調(diào)姿機構(gòu)已在飛機機身、機翼等大部件自動調(diào)姿中獲得成功應(yīng)用，為此，本文以中機身自動調(diào)姿機構(gòu)為具體研究對象，其誤差分析過程具有典型意義。引入SDT，用小位移旋量表示調(diào)姿機構(gòu)制造誤差；結(jié)合微分變換和5次多項式軌跡規(guī)劃方法建立單個定位器動態(tài)誤差的傳遞表達式；針對多個定位器誤差耦合，引入測量學(xué)中的間接平差理論，將工藝接頭球鉸中心的位置坐標(biāo)視為測量點，結(jié)合測量學(xué)

中的改正數(shù)計算式和加權(quán)最小二乘法，推導(dǎo)調(diào)姿機構(gòu)動態(tài)誤差耦合計算表達式，以獲得裝配部件位姿參數(shù)的波動區(qū)間和實時誤差補償量。

1 中機身調(diào)姿坐標(biāo)系構(gòu)建

圖1和圖2所示為三坐標(biāo)定位器式中機身調(diào)姿機構(gòu)，該調(diào)姿機構(gòu)由4個三坐標(biāo)定位器組成，利用鉤頭螺栓將中機身與調(diào)姿機構(gòu)托架固連，定位接頭與定位器通過球鉸副連接，各定位器結(jié)構(gòu)相同， 均由z向伸縮柱和滾珠絲杠驅(qū)動的x、y向?qū)к壗M成。中機身的位姿調(diào)整由4個定位器并聯(lián)驅(qū)動。

圖1 4定位器式中機身調(diào)姿機構(gòu)
Fig.1Mechanism for fuselage posture adjustment with four positioners

為描述方便，建立圖1和圖2所示的坐標(biāo)系：① 中機身坐標(biāo)系Ofxfyfzf；② 定位接頭坐標(biāo)系Ojxjyjzj，4個定位接頭坐標(biāo)系分別記為Oj1xj1yj1zj1、Oj2xj2yj2zj2、Oj3xj3yj3zj3和Oj4xj4yj4zj4；③z向伸縮柱坐標(biāo)系Opxpypzp，z向伸縮柱坐標(biāo)系的坐標(biāo)原點和定位接頭坐標(biāo)系的坐標(biāo)原點重合，均為定位接頭球鉸中心點； ④x向?qū)к壸鴺?biāo)系Os1xs1ys1zs1； ⑤y向?qū)к壸鴺?biāo)系Os2xs2ys2zs2。各坐標(biāo)系之間的位姿關(guān)系用φ、θ、ψ、x、y、z等6個參數(shù)表示。φ、θ、ψ是歐拉角，表示兩坐標(biāo)系之間的姿態(tài)關(guān)系，如果調(diào)姿機構(gòu)沒有制造誤差，Opxpypzp、Os1xs1ys1zs1、Os2xs2ys2zs2之間的姿態(tài)角均為0°；x、y、z是坐標(biāo)值，表示兩坐標(biāo)系之間的位置關(guān)系。

2 中機身自動調(diào)姿機構(gòu)誤差分析與建模

圖3 定位器零部件形位誤差
Fig.3 Shape and position errors of positioner parts

分析中機身自動調(diào)姿工藝可知，影響中機身調(diào)姿精度的因素主要包括：①調(diào)姿機構(gòu)零部件制造誤差；②數(shù)控驅(qū)動；③調(diào)姿機構(gòu)零部件磨損；④溫度變化引起的變形；⑤調(diào)姿機構(gòu)受力變形。某型號飛機A類位姿測量點球形位置公差帶的半徑為0.3 mm[19]，與調(diào)姿精度要求相比：調(diào)姿機構(gòu)零部件強度剛度均較大；裝配車間內(nèi)溫度波動較小，溫度影響可忽略不計；零部件磨損引起的誤差也較小。為此，本文以調(diào)姿機構(gòu)制造誤差為分析對象，圖3所示為影響中機身調(diào)姿精度的調(diào)姿機構(gòu)零部件制造誤差項。

2.1 基于SDT的調(diào)姿機構(gòu)誤差建模

利用基于SDT的公差建模方法，將調(diào)姿機構(gòu)各零部件幾何特征的形位、尺寸、裝配間隙等誤差統(tǒng)一用τ表示，τ=[dδ]T，其中，d=[dxdydz]為平動分量集，δ=[ΔθxΔθyΔθz]為轉(zhuǎn)動分量集。各誤差項傳遞時，將τ寫成齊次變換矩陣：

2.2 基于SDT的零件幾何特征誤差累積

利用SDT的齊次變換矩陣形式，可得

(1)

(2)

(3)

結(jié)合式(1)～式(3)可知，零件裝配位姿誤差為零件上各幾何特征SDT誤差參數(shù)的對應(yīng)項直接累加。

3 單個定位器誤差傳遞與累積

3.1 定位接頭

3.1.1 基于SDT的定位接頭誤差建模

如圖3所示，將定位接頭各誤差項的SDT分別記為

(4)

式中：上標(biāo)j表示定位接頭；下標(biāo)R表示圓度誤差，PO表示位置度誤差，RO表示圓跳動誤差，TC表示球鉸間隙誤差，DT表示尺寸誤差。

利用式(3)，可得定位接頭各誤差項SDT旋量參數(shù)累積表達式為

(5)

3.1.2 基于微分變換的定位接頭誤差傳遞

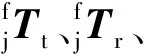
在定位接頭坐標(biāo)系Ojxjyjzj中，有

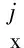
(6)

化簡式(6)，可得

(7)

式中:

在中機身坐標(biāo)系Ofxfyfzf中

(8)

整理式(8)，可得

(9)

式中:

(10)

(11)

式中:

經(jīng)計算

(12)

(13)

(14)

式中：

化簡式(14)，可得

(15)

(16)

3.2 z向伸縮柱和x、y向?qū)к?/h3>

依據(jù)定位器接頭誤差分析方法進行z向伸縮柱和x、y向?qū)к壍恼`差傳遞與累積。

3.2.1z向伸縮柱

將圖3所示z向伸縮柱各誤差項的SDT分別表示為

式中：上標(biāo)p表示z向伸縮柱；下標(biāo)C表示圓柱度誤差；V表示垂直度誤差；A表示同軸度誤差。

再次利用式(3)，可得z向伸縮柱各誤差項SDT旋量參數(shù)累積為

(17)

3.2.2x向?qū)к?/p>

將圖3所示x向?qū)к壐髡`差項的累積SDT分別表示為

式中：上標(biāo)s1表示x向?qū)к墸幌聵?biāo)S表示直線度誤差，F(xiàn)表示平面度誤差，P表示平行度誤差。

(18)

3.2.3y向?qū)к?/p>

將圖3所示y向?qū)к壐髡`差項的累積SDT分別表示為

式中：上標(biāo)s2表示y向?qū)к墶?/p>

(19)

3.3 5次多項式調(diào)姿軌跡規(guī)劃

調(diào)姿過程中應(yīng)避免啟動和停止沖擊，中機身起始位姿為標(biāo)定值，終止位姿為對接裝配目標(biāo)位姿，因此，中機身調(diào)姿需滿足以下約束條件：① 起始速度、終止速度分別為“0”；②起始加速度、終止加速度分別為“0”；③ 調(diào)姿初始位姿Xs=[xsyszsφsθsψs]T，調(diào)姿終止位姿Xe=[xeyezeφeθeψe]T。由調(diào)姿約束條件可知，調(diào)姿軌跡規(guī)劃有6個約束，可用5次多項式實現(xiàn)調(diào)姿過程中的軌跡擬合：

f(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

(20)

式中：a0～a5為多項式系數(shù)，t表示時間。利用約束條件求解式(20)，可得中機身運動軌跡方程為

(21)

式中：t0為調(diào)姿初始時間；te為調(diào)姿終止時間。

利用式(21)，可求得定位接頭球心Pi的坐標(biāo)為

Pi=RPfi+Po

(22)

式中：Pfi為定位接頭球心在坐標(biāo)系Ofxfyfzf中的坐標(biāo)；Po為坐標(biāo)系Ojxjyjzj相對于坐標(biāo)系Ofxfyfzf的位置；R為旋轉(zhuǎn)矩陣。

利用式(22)，可求得定位器各局部坐標(biāo)系的位置坐標(biāo)

(23)

3.4 單個定位器誤差傳遞與累積

3.4.1 單個定位器4層次誤差傳遞與累積

聯(lián)立式(14)、式(17)～式(19)，可求得單個定位器各零部件制造誤差引起的中機身調(diào)姿累積誤差為

(24)

式中：df=[dfxdfydfz]、δf=[ΔθfxΔθfyΔθfz]分別為中機身位置誤差和姿態(tài)誤差。

由于伸縮柱坐標(biāo)系Opxpypzp原點與定位接頭坐標(biāo)系Ojxjyjzj重合，經(jīng)簡單計算可得

(25)

(26)

3.4.2 誤差分析

從式(26)可看出中機身位姿誤差與單個定位器制造誤差的關(guān)系為：①中機身姿態(tài)誤差僅與各誤差項的姿態(tài)誤差相關(guān)，與位置誤差無關(guān)，姿態(tài)誤差的傳遞系數(shù)為各誤差項所在坐標(biāo)系相對于中機身部件坐標(biāo)系的齊次變換矩陣；②中機身位置誤差與各誤差項的位置、姿態(tài)誤差均有關(guān)。

由式(26)可知，df、δf均為各誤差項SDT的線性累加。如果定位器為批量生產(chǎn)，各誤差項為相互獨立的正態(tài)分布，df、δf也應(yīng)服從正態(tài)分布。則df、δf的數(shù)學(xué)期望E((df)T)、E((δf)T)計算表達式為

根據(jù)多個觀測值線性函數(shù)的協(xié)方差陣計算方法[20]，df、δf的協(xié)方差陣D((df)T)、D((δf)T)計算表達式為

式中：D((dj)T)、D((dp)T)、D((ds1)T)、D((ds2)T)、D((δj)T)、D((δp)T)、D((δs1)T)、D((δs2)T)均為方差陣。

4 基于間接平差法的多定位器誤差耦合

4.1 多定位器制造誤差耦合

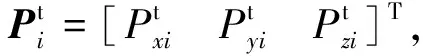
(27)

式中：

(28)

(29)

利用rR、Pt、Pr將式(29)進行擴展，得

(30)

圖4 調(diào)姿實際位姿與調(diào)姿理論位姿關(guān)系模型
Fig.4Model for relationship between real posture and theoretical posture

4.2 基于間接平差法的多定位器耦合誤差求解

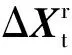
利用式(30)可求得定位器制造誤差耦合的間接平差方程為

(31)

式中：V為改正數(shù)；ΔP=Pr-Pt。

利用式(27)，可求得點pi的坐標(biāo)誤差ΔPi為

(32)

式中：Δθix、Δθiy、Δθiz為點pi引起的姿態(tài)誤差；dti為點pi引起的位置誤差。

利用式(32)，對ΔPi進行擴展，構(gòu)建所有球鉸中心點的坐標(biāo)誤差矩陣為

(33)

(34)

化簡式(34)，得

(rR)TWV=0

(35)

(36)

由于各定位器均為獨立制造，其制造安裝精度指標(biāo)均相同，可取W為單位陣，并將式(36)改寫為

(37)

對式(37)求一階、二階導(dǎo)數(shù)，可求得中機身調(diào)姿速度誤差和加速度誤差。

4.3 定位器驅(qū)動誤差反饋

(38)

利用式(38)進行定位器x、y、z方向驅(qū)動量的動態(tài)補償，可提高裝配部件的位姿精度。對式(38)求一階、二階導(dǎo)數(shù)，可求得定位器x方向、y方向和z方向的速度誤差和加速度誤差。

5 試 驗

依據(jù)圖1所示的調(diào)姿機構(gòu)原理圖，搭建圖5所示的調(diào)姿試驗機構(gòu)，中機身用模擬件代替。該試驗機構(gòu)4個定位器x向、y向?qū)к壭谐叹鶠?00 mm，z向伸縮柱行程均為400 mm。表1所示為調(diào)姿機構(gòu)制造誤差檢測值；表2所示為坐標(biāo)系Ojxjyjzj相對坐標(biāo)系Ofxfyfzf的位置；表3所示為坐標(biāo)系Ojxjyjzj相對坐標(biāo)系Ofxfyfzf的姿態(tài)角。表4所示為模擬件調(diào)姿試驗初始位姿和目標(biāo)位姿，各調(diào)姿試驗?zāi)M件的初始位姿、目標(biāo)位姿均相同。試驗總調(diào)姿時間均為200 s。試驗過程中采用輔助測量桿對z向伸縮柱進行初始位置標(biāo)定，利用測量靶球?qū)崿F(xiàn)x、y向?qū)к壋跏嘉恢玫臉?biāo)定。利用型號為AT402的萊卡激光跟蹤儀進行模擬件位姿測量。萊卡AT402激光跟蹤儀的距離分辨率≤0.1 μm；絕對距離測量精度全量程范圍內(nèi)不超過10 μm；絕對距離重復(fù)性為5 μm。

圖5 中機身調(diào)姿試驗機構(gòu)
Fig.5Experiment mechanism for fuselage posture adjustment

-

Continued

表2 坐標(biāo)系Ojxjyjzj相對坐標(biāo)系Ofxfyfzf的位置

表3 坐標(biāo)系Ojxjyjzj相對坐標(biāo)系Ofxfyfzf的姿態(tài)角

表4 調(diào)姿初始位姿和目標(biāo)位姿Table 4 Initial and target postures of adjustment

5.1 試驗機構(gòu)驅(qū)動修正值計算

試驗前，結(jié)合式(37)和式(38)，利用MATLAB計算出各定位器驅(qū)動誤差，依據(jù)驅(qū)動誤差得到如圖6所示的各定位器驅(qū)動修正值。

由圖6可明顯看出，各定位器補償量曲線具有很好的連續(xù)性、平緩、無突變，易于由運動控制系統(tǒng)實現(xiàn)。調(diào)姿過程中，各定位器的補償量不是常量，隨著調(diào)姿部件位姿的變換而改變；補償量存在較大差異，補償量范圍為-0.675～0.814 mm。

圖6 各定位器驅(qū)動修正值
Fig.6 Driving correction values of positioners

5.2 調(diào)姿試驗

首先，對沒有實施驅(qū)動補償?shù)恼{(diào)姿機構(gòu)進行試驗，利用激光跟蹤儀測量不同調(diào)姿時刻中機身上4個測量靶球的坐標(biāo)值，利用靶球的測量坐標(biāo)值求解出中機身的位姿誤差；依據(jù)位姿誤差，繪制圖7所示的位置和姿態(tài)誤差曲線圖。然后，依據(jù)圖6所示的各定位器驅(qū)動修正值對試驗機構(gòu)各方向驅(qū)動量進行補償，利用激光跟蹤儀測量靶球的坐標(biāo)值，求解不同調(diào)姿時刻中機身的位姿誤差；依據(jù)位姿誤差，繪制實施驅(qū)動補償后的位姿誤差曲線圖，如圖8所示。

由圖8可看出，調(diào)姿過程中，試驗機構(gòu)的位姿誤差是個動態(tài)值。位姿誤差不僅與各定位器的制造精度、定位器的分布、定位器數(shù)量等存在強非線性耦合關(guān)系，還與運動軌跡存在耦合關(guān)系。對比試驗位姿誤差可知，無驅(qū)動修正時，位置誤差波動范圍為-0.163～0.222 mm，姿態(tài)角誤差波動范圍為-9.2×10-4～6.0×10-4(°)。實施驅(qū)動修正后，位置誤差波動范圍為-0.122～0.158 mm，姿態(tài)角誤差波動范圍為-4.8×10-4～3.1×10-4(°)。

利用圖7和圖8所示的調(diào)姿位姿誤差試驗數(shù)據(jù)，可得實施驅(qū)動修正前后的位姿誤差的絕對平均誤差、標(biāo)準(zhǔn)偏差和終點誤差(表5)。

由表5可知，實施驅(qū)動修正后，到達目標(biāo)位姿時，模擬件位置誤差范圍由修正前的-0.100～0.127 mm降低為-0.069～0.084 mm，角度誤差范圍由-5.6×10-4～1.22×104(°)降低為-8.5×10-5～1.22×10-4(°)，各位姿參數(shù)的絕對平均誤差和標(biāo)準(zhǔn)差也均有較大幅度的減少。

綜合以上試驗結(jié)果可知，利用本文提出的裝配部件動態(tài)調(diào)姿精度預(yù)測與驅(qū)動補償量計算方法，能實現(xiàn)裝配部件的調(diào)姿精度量化預(yù)測和誤差補償量的實時計算與反饋。調(diào)姿精度量化分析為數(shù)字化自動調(diào)姿機構(gòu)的公差設(shè)計提供了理論依據(jù)，動態(tài)誤差補償為保證飛機大部件裝配協(xié)調(diào)準(zhǔn)確度提供了可行途徑。

圖7 無驅(qū)動補償?shù)闹袡C身調(diào)姿誤差
Fig.7 Errors of fuselage posture-adjusting without driving compensation

圖8 驅(qū)動補償后的中機身調(diào)姿誤差
Fig.8 Errors of fuselage posture-adjusting with driving compensation

PositionandposeerrorPositionandposeFinalpositionerrorMeanabsoluteerrorStandarderrorx/mm-0．0670．0820．087y/mm0．1270．1710．185Withoutdrivingcompensationz/mm-0．1000．1320．142φ/(°)1．3×10-41．6×10-45．7×10-5θ/(°)4．7×10-45．4×10-41．9×10-4ψ/(°)-5．6×10-47．4×10-42．6×10-4x/mm-0．0640．0820．088y/mm0．0840．1100．124Withdrivingcompensationz/mm-0．0690．0870．094φ/(°)3．62×10-53．40×10-53．2×10-5θ/(°)1．22×10-41．26×10-41．0×10-4ψ/(°)-8．10×10-51．31×10-41．4×10-4

6 結(jié) 論

1) 針對飛機中機身自動調(diào)姿誤差傳遞及其精度分析，綜合運用小旋量理論、微變齊次變換、間接平差法和加權(quán)最小二乘法，提出了一套完整的中機身調(diào)姿精度預(yù)測與動態(tài)誤差補償計算方法。

2) 試驗結(jié)果表明，利用提出的裝配部件動態(tài)調(diào)姿精度預(yù)測與驅(qū)動補償計算方法能實現(xiàn)裝配部件的調(diào)姿精度量化預(yù)測和誤差補償量實時計算與反饋，依據(jù)誤差補償量對調(diào)姿機構(gòu)實施誤差補償，能提高試驗件的定位精度，減少調(diào)姿誤差。

3) 飛機各大部件調(diào)姿機構(gòu)的定位器數(shù)量、結(jié)構(gòu)和誤差項可能會存在差異，但本文提出的誤差傳遞與耦合模型的推導(dǎo)過程具有較好的通用性，可以推廣到具有不同數(shù)量定位器和不同誤差項的飛機大部件調(diào)姿機構(gòu)，也可應(yīng)用于其他類似的并聯(lián)機構(gòu)。

致 謝

本文涉及的試驗系統(tǒng)研制得到了南京航空航天大學(xué)黃翔教授及其帶領(lǐng)團隊的協(xié)助，特此致謝。

[1] 許國康. 大型飛機自動化裝配技術(shù)[J]. 航空學(xué)報, 2008, 29(3): 734-740.

XU G K. Automatic assembly technology for large aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(3): 734-740 (in Chinese).

[2] 范玉青, 梅中義, 陶劍. 大型飛機數(shù)字化制造工程[M]. 北京: 航空工業(yè)出版社, 2011: 843-844.

FAN Y Q, MEI Z Y, TAO J. Digital manufacturing engineering of large aircraft[M]. Beijing: Aviation Industry Press, 2011: 843-844 (in Chinese).

[3] 林雪竹, 李麗娟, 曹國華, 等. 大部件對接iGPS高精度位姿測量優(yōu)化設(shè)計[J]. 航空學(xué)報, 2015, 36 (4): 1299-1311.

LIN X Z, LI L J, CAO G H, et al. Optimal design based on iGPS high-precision posture measurement for large size component joining[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1299-1311 (in Chinese).

[4] 郭志敏, 蔣君俠, 柯映林. 基于POGO 柱三點支撐的飛機大部件調(diào)姿方法[J]. 航空學(xué)報, 2009, 30(7): 1320-1331.

GUO Z M, JIANG J X, KE Y L. Posture alignment for large aircraft parts based on three POGO sticks distributed support[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(7): 1320-1331 (in Chinese).

[5] 熊瑞斌, 黃浦縉, 柯映林. 一種適用于飛機裝配的新型隨動定位器[J]. 航空學(xué)報, 2009, 30(12): 2469-2475.

XIONG R B, HUANG P J, KE Y L. A new posture following and keeping fixture for aircraft assembly[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(12): 2469-2475 (in Chinese).

[6] ZHU Y G, HUANG X, FANG W, et al. Trajectory planning algorithm based on quaternion for 6 DOF aircraft wing automatic position and pose adjustment method[J]. Chinese Journal of Aeronautics, 2010, 23(6): 707-714.

[7] 雷沛, 鄭聯(lián)語. 面向飛機大部件調(diào)姿的PPPS機構(gòu)球鉸點中心位置閉環(huán)標(biāo)定方法[J]. 航空學(xué)報, 2016, 37(10): 3186-3196.

LEI P, ZHENG L Y. Closed-loop calibration method of PPPS mechanism ball joint center position for posture adjustment of large aircraft component[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 3186-3196 (in Chinese).

[8] 李晨, 方強, 李江雄. 基于三坐標(biāo)定位器的大部件調(diào)姿機構(gòu)誤差分析[J]. 機電工程, 2010, 27(3): 6-12.

LI C, FANG Q, LI J X. Error analysis of 3-axis locator based pose adjustment mechanism[J]. Journal of Mechanical & Electrical Engineering, 2010, 27(3): 6-12 (in Chinese).

[9] 郭飛燕, 王仲奇, 康永剛, 等.飛機立柱式柔性工裝定位誤差分析與精度保障[J]. 計算機集成制造系統(tǒng), 2013,19(8): 2036-2042.

GUO F Y, WANG Z Q, KANG Y G, et al. Error analysis and accuracy guarantee for column flexible tooling positioning of aircraft[J]. Computer Integrated Manufacturing Systems, 2013, 19(8): 2036-2042 (in Chinese).

[10] 郭志敏, 蔣君俠, 柯映林.一種精密三坐標(biāo)POGO 柱設(shè)計與精度研究[J]. 浙江大學(xué)學(xué)報(工學(xué)版), 2009, 43(9): 1649-1654.

GUO Z M, JIANG J X, KE Y L. Design and accuracy for POGO stick with three axes[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(9): 1649-1654(in Chinese).

[11] 朱永國, 黃翔, 方偉, 等. 機身自動調(diào)姿方法及誤差分析[J]. 南京航空航天大學(xué)學(xué)報, 2011, 43(2): 229-234.

ZHU Y G, HUANG X, FANG W, et al. Fuselage automatic position and pose adjustment method and its error analysis[J]. Journal of Nanjing University of Aeronautics &Astronautics, 2011, 43(2): 229-234 (in Chinese).

[12] 朱永國. 飛機大部件自動對接若干關(guān)鍵技術(shù)研究[D]. 南京: 南京航空航天大學(xué), 2011: 35-39.

ZHU Y G. Research on some key techniques on aircraft large part automatic joining[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011: 35-39 (in Chinese).

[13] BOURDET P, MATHIEU L, LARTIGUE C, et al. The concept of the small displacement torsor in metrology[J]. Advanced Mathematical Tools in Metrology, 1996(40): 110-122.

[14] VILLENEUVE F, VIGNAT F. Advances in integrated design and manufacturing in mechanical engineering[M]. Berlin: Springer Netherlands, 2005: 189-200.

[15] ASANTE J N. A small displacement torsos model for tolerance analysis in a workpiece-fixture assembly[J]. Journal of Engineering Manufacture, 2009, 223(8): 1005-1020.

[16] 彭和平. 基于新一代GPS 框架的公差設(shè)計理論與方法研究[D]. 武漢: 華中科技大學(xué), 2009: 31-34.

PENG H P. Study on theory and methodology of tolerance design within the framework of the new generation GPS standards system[D]. Wuhan: Huazhong University of Science and Technology, 2009: 31-34 (in Chinese).

[17] 茅健, 張恒, 曹衍龍. 基于SDT的平面尺寸公差模型研究及應(yīng)用[J]. 工程設(shè)計學(xué)報, 2010, 17(5): 321-324.

MAO J, ZHANG H, CAO Y L. Research and application on model of size tolerance for plane based on SDT[J]. Journal of Engineering Design, 2010, 17(5): 321-324 (in Chinese).

[18] 呂程, 劉子建, 艾彥迪, 等. 多公差耦合裝配結(jié)合面誤差建模與公差優(yōu)化設(shè)計[J]. 機械工程學(xué)報, 2015, 51(18): 108-118.

Lü C, LIU Z J, AI Y D, et al. Assembly joint surface error modeling and tolerance optimization in the case of coupled tolerance[J]. Journal of Mechanical Engineering, 2015, 51(18): 108-118 (in Chinese).

[19] 劉楚輝. 飛機機身數(shù)字化對接裝配中的翼身交點加工關(guān)鍵技術(shù)研究[D]. 杭州： 浙江大學(xué), 2011: 99.

LIU C H. Study on key techniques of wing-fuselage joins machining in digital aircraft assembly[D].Hangzhou: Zhejiang University, 2011: 99 (in Chinese).

[20] 陶本藻，邱衛(wèi)寧. 誤差理論與測量平差基礎(chǔ)[M]. 武漢: 武漢大學(xué)出版社, 2009: 27-31, 106-111.

TAO B Z, QIU W N. Error theory and measurement adjustment basis[M]. Wuhan: Wuhan University Press, 2009: 27-31, 106-111 (in Chinese).

[21] 于成浩, 柯明. 基于激光跟蹤儀的測量控制網(wǎng)測量精度分析[J]. 測繪科學(xué), 2006, 31(3): 25-27.

YU C H, KE M. The measurement accuracy analysis of three dimensional control network based on laser tracker[J]. Science of Surveying and Mapping, 2006, 31(3): 25-27 (in Chinese).

AccuracyanalysisforautomaticaladjustmentofaircraftfuselageposturebasedonSDTandindirectadjustment

ZHUYongguo1,*,ZHANGWenbo1,LIUChunfeng2,ZHAOShuang2

1.SchoolofAeronauticalManufacturingEngineering,NanchangHangkongUniversity,Nanchang330063,China2.AVICJiangxiHongduAviationIndustryGroupCompanyLtd.,Nanchang330024,China

Thispaperdiscussesthemechanismforadjustingaircraftfuselagewithfourpositioners.Acalculationmethodisproposedtoanalyzedynamicposture-adjustingaccuracyofaircraftparts.TheSmallDisplacementTorsor(SDT)isusedtomodelthecriticaltolerancesofthepositioner,andtheSDTmodeloffourlevelerrorsisestablishedforthepositioner.Anexplicitfunctionrelationshipbetweenmanufacturingerrorsandfuselage’spostureerrorisbuiltbasedondifferentialtransformmethod,andthetransferandaccumulationcoefficientmatricesofmanufacturingerrorsarealsoderived.Amathematicalmodelfordynamicerrortransferofasinglepositionerisestablishedusingthefive-orderpolynomialtrajectoryplanningmethod.Then,toovercomeerrorcouplingofmulti-positioner,amethodforcalculatingdynamicerrorcouplingofmulti-positionersphericalcentersisproposedbyusingindirectadjustmentmethodandweightedleastsquaremethod,andtheexpressionforerrorcompensationisalsoderived.Thetestdatashowthatpositionandposeerrorscanbereduced,andposture-adjustingaccuracycanbeimprovedwithdrivingcompensationaccordingtotheproposedmethod,whichcanthusprovideaneffectivewaytoensureassemblecoordinationaccuracyoflargecomponents.

aircraft;assembly;fuselage;SmallDisplacementTorsor(SDT);indirectadjustment;errortransfer;errorcoupling

2017-04-05；

2017-05-10；

2017-07-03；Publishedonline2017-08-211928

URL：http://hkxb.buaa.edu.cn/CN/html/20171228.html

s：NationalNaturalScienceFoundationofChina(51565042)；FocusonResearchandDevelopmentPlansinJiangxiProvince(20161BBE53005，20171BBE50007)

.E-mailzhuyongguo_2003@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.421301

2017-04-05；退修日期2017-05-10；錄用日期2017-07-03；網(wǎng)絡(luò)出版時間2017-08-211928

http://hkxb.buaa.edu.cn/CN/html/20171228.html

國家自然科學(xué)基金(51565042)； 江西省重點研發(fā)計劃(20161BBE53005,20171BBE50007)

.E-mailzhuyongguo_2003@163.com

朱永國，張文博，劉春鋒，等. 基于SDT和間接平差的中機身自動調(diào)姿精度分析J． 航空學(xué)報,2017,38(12):421301.ZHUYG,ZHAGNWB,LIUCF,etal.AccuracyanalysisforautomaticaladjustmentofaircraftfuselageposturebasedonSDTandindirectadjustmentJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):421301.

V262.4

A

1000-6893(2017)12-421301-14

李世秋)