正六邊形鋼管約束混凝土靶抗侵徹性能的數值模擬

蒙朝美,蔣志剛,蔡良才,劉 飛,譚清華

(1.空軍工程大學 機場建筑工程系,陜西 西安 710038;2.國防科學技術大學 基礎教育學院,湖南 長沙 410072)

正六邊形鋼管約束混凝土靶抗侵徹性能的數值模擬

蒙朝美1,2,蔣志剛2,蔡良才1,劉 飛2,譚清華2

(1.空軍工程大學 機場建筑工程系,陜西 西安 710038;2.國防科學技術大學 基礎教育學院,湖南 長沙 410072)

正六邊形鋼管約束混凝土靶具有優良的抗侵徹性能。基于12.7 mm穿甲彈侵徹試驗,運用ANASYS/LS-DYNA軟件,分析了正六邊形鋼管約束混凝土靶的鋼管壁厚和邊長對抗侵徹性能的影響;考慮效費比,分析了鋼管約束混凝土靶的經濟性能。結果表明:適當增加鋼管壁厚和減小邊長可提高正六邊形鋼管約束混凝土靶的抗侵徹性能;優化鋼管壁厚和邊長的匹配可以得到較好的抗侵徹能力和經濟性,對于該文所用彈丸,較優匹配為邊長37.5 mm、壁厚3.5 mm。研究結果可為鋼管約束混凝土遮彈結構設計提供參考。

防護結構;約束混凝土;侵徹性能;數值模擬

侵徹試驗和數值模擬表明鋼管約束混凝土具有優良的抗侵徹性能。文獻[1～3]開展了12.7 mm穿甲彈單發和多發侵徹圓形鋼管約束混凝土靶試驗,蒙朝美等[4]開展了12.7 mm穿甲彈侵徹多邊形鋼管約束混凝土靶試驗,王起帆等[5]進行了蜂窩遮彈層抗彈丸侵徹試驗,試驗結果均表明約束混凝土具有優良的抗侵徹性能。石少卿等[6]和李季等[7]分別對仿生蜂窩遮彈層和鋼管鋼纖維混凝土遮彈層的抗侵徹性能進行了數值模擬。武珺等[8]進行了正六邊形鋼管約束混凝土靶抗侵徹性能數值模擬,表明鋼管約束混凝土靶具有優良的抗侵徹性能。蔣志剛等[9]和蒙朝美等[4]利用ANSYS/LY-DYNA分別深入分析了圓形和正六邊形鋼管約束混凝土靶的抗侵徹機理。壁厚和邊長是決定正六邊形鋼管的關鍵因素,既影響鋼管約束混凝土靶的抗侵徹性能,還影響其經濟性。因此,研究壁厚和邊長對正六邊形鋼管約束混凝土靶抗侵徹性能的影響規律有重要的應用價值。

本文在文獻[4]的基礎上,基于12.7 mm穿甲彈侵徹正六邊形鋼管約束混凝土靶試驗,運用LS-DYNA軟件,采用有限元-光滑粒子法,研究鋼管壁厚和邊長對正六邊形鋼管約束混凝土靶抗侵徹性能的影響,并考慮效費比,得到了較優的邊長與壁厚的匹配方案。

1 仿真模型與試驗驗證

1.1 仿真模型

為了探究正六邊形鋼管約束混凝土靶的抗侵徹性能,文獻[4]進行了正六邊形鋼管約束混凝土靶抗侵徹性能試驗,彈丸為12.7 mm鎢芯彈,質量48 g,長59.5 mm,結構如圖1所示,其中鎢芯直徑dw=7.5 mm,長34.3 mm,質量19.7 g。彈丸垂直入射靶心(實際偏心距小于10 mm),試驗后鎢芯變形很小,可視為剛體。正六邊形鋼管由3.5 mm厚(δ)鋼板焊接而成,邊長(a)80.5 mm,外接圓直徑d=161 mm;靶厚350 mm。核心混凝土實測密度為2 420 kg/m3,邊長150 mm,標準立方體抗壓強度和劈裂強度分別為66.2 MPa和5.66 MPa,直徑150 mm、高度300 mm且圓柱體軸心抗壓強度為54.3 MPa。

與文獻[10]相同,仿真模型按中心正入射處理, 利用對稱性取1/2結構建模。混凝土中心區域半徑20 mm(約5倍彈徑)范圍內采用光滑粒子,共劃分50 400個粒子;其他部分均采用Lagrange網格、SOLID164六面體實體單元,小變形區混凝土單元尺寸逐漸過渡,粒子附近的混凝土單元較細,鋼管附近的混凝土單元較粗,外圍混凝土共劃分146 160個單元;鋼管沿厚度方向劃分2個單元,共劃分10 080個單元;靶的網格模型如圖2所示。彈丸按銅皮、鋼套和鎢芯建模,銅皮共劃分750個單元,鋼套共劃分486個單元,鎢芯共劃分856個單元,網格模型如圖3所示。光滑粒子與彈丸間采用點面侵蝕算法,彈丸的鎢芯與銅皮、鎢芯與鋼套、銅皮與鋼套間均采用面面侵蝕算法,混凝土光滑粒子與有限元網格間采用固連點面接觸,混凝土與鋼管間采用固連面面接觸。鋼管側面、靶體正面為自由邊界,彈道剖面為對稱邊界,靶背面沿軸向位移為0。

鎢芯采用剛體模型,鋼套和鋼管采用隨動硬化模型,銅皮采用JC模型,混凝土采用帽蓋模型,具體參數見文獻[10]。

1.2 試驗驗證

表1給出了文獻[4]中典型工況侵徹深度hp模擬結果與試驗結果的比較,表中e為侵徹深度的相對誤差。由表1可見,兩者吻合較好,最大誤差為2.6%。

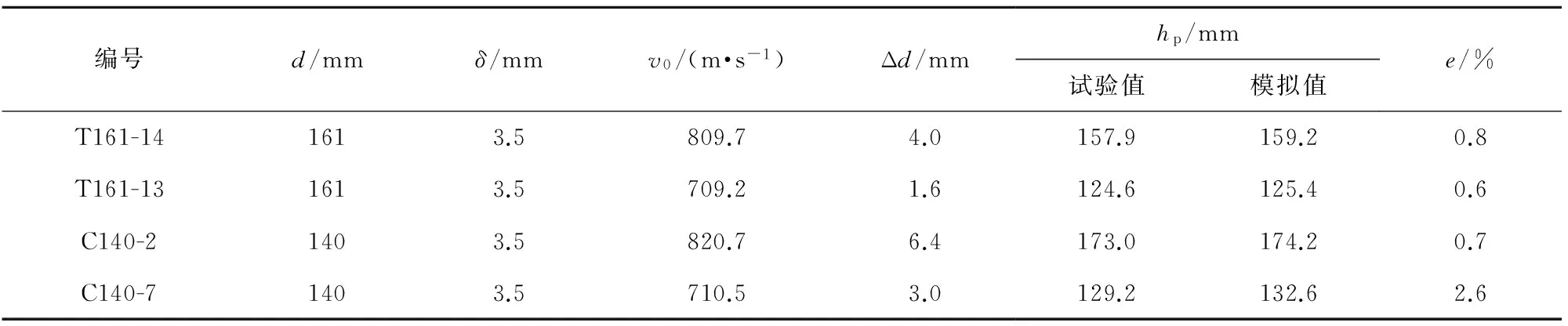
表1 侵徹深度模擬結果與試驗比較

圖4給出了表1中編號T161-13試件的試驗結果(左圖)與本文數值模擬結果(右圖)的比較。其中:模擬結果為侵徹結束時的損傷(D值)云圖,圖4(b)為過兩對邊中點所在剖面;試驗偏心距Δd=1.6 mm,撞擊速度v0=709.2 m/s。

由圖4可知:混凝土表面裂紋的分布和彈丸侵徹深度的模擬結果與試驗吻合良好。模擬結果(未考慮偏心的影響)的損傷云圖基本對稱,迎彈面有大量完全損傷的粒子飛離靶體,與試驗中迎彈面成坑時混凝土碎片飛濺現象相吻合;混凝土表面損傷云圖較好地體現了試驗靶體的側面裂紋分布情況。因此,本文仿真模型和材料參數合理,可用于研究鋼管邊長和壁厚對正六邊形鋼管約束混凝土靶抗侵徹性能的影響。

2 模擬工況及結果分析

2.1 模擬工況

取撞擊速度為820 m/s,中心正入射,按上述方法計算,網格大小基本相同。僅改變鋼管的壁厚和邊長,比較不同規格靶的侵徹深度,計算工況及侵徹深度模擬結果如表2所示,表中ω為含鋼率。其中,混凝土等效直徑為鋼管內壁內切圓直徑,彈芯即為鎢芯;組別1和組別2主要考察邊長的影響,壁厚分別為3.5 mm和6 mm;T77、T83和組別3可考察鋼管壁厚的影響,混凝土的等效直徑(dq)相同,為60 mm;組別4主要考察組別1中較優規格工況(T95-3.5)條件下,鋼管邊長與壁厚匹配的影響,含鋼率相同(約為16.3%);組別5模擬半無限靶,作為對比。

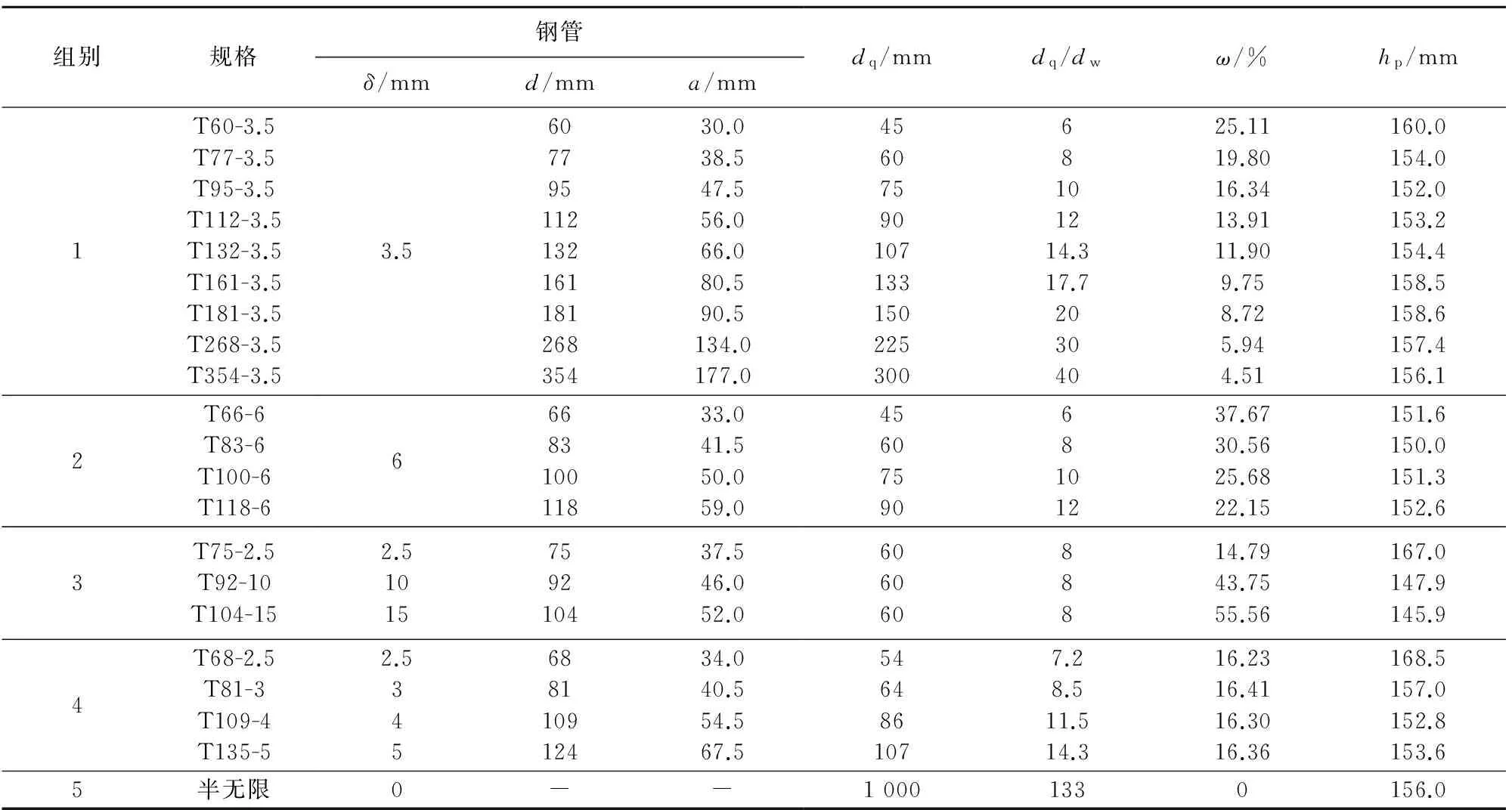
表2 模擬工況(v0=820 m/s)

注:組別1～4規格欄中,第一個數字表示鋼管外接圓直徑,第二個數字表示壁厚。

2.2 模擬結果分析

表2結果表明:所有工況中侵徹深度最小值為145.9 mm(T104-15),最大值為168.5 mm(T68-2.5),分別較半無限靶減小6.5%和增大了8.0%。其原因是鋼管規格對鋼管約束混凝土靶的混凝土自約束作用(外圍變形較小混凝土對彈孔附近變形較大混凝土的約束作用)和鋼管對核心混凝土的徑向約束作用的非線性影響[9],鋼管約束混凝土靶的侵徹深度可能大于或小于半無限混凝土靶。

2.2.1 邊長的影響

圖5(a)和圖5(b)分別給出了鋼管壁厚為3.5 mm和6 mm工況下侵徹深度hp隨邊長a的變化關系。由圖5可知:

①當鋼管壁厚固定,邊長變化時,侵徹深度存在極小值,即存在較優的邊長。當壁厚為3.5 mm時,較優邊長為47.5 mm左右,侵徹深度極小值約為152 mm,此時含鋼率約為16%,混凝土等效直徑與彈芯直徑比值約為10,鋼管邊長與壁厚比值約為13.5;當壁厚為6 mm時,較優邊長為41.5 mm左右,侵徹深度極小值約為150 mm,此時含鋼率約為30.6%,混凝土等效直徑與彈芯直徑比值約為8,鋼管邊長與壁厚比值約為6.9。

②當邊長大于較優值時,隨著邊長的增大,混凝土自約束作用增強,而鋼管的約束作用減小,導致侵徹深度先增大,然后緩慢減小,最后趨于半無限靶。

③當邊長小于較優值時,隨著邊長的減小,鋼管的約束作用增強,但混凝土的自約束作用減弱,侵徹深度增大;當邊長小于某一臨界值時,鋼管可能出現屈服,約束作用減弱,侵徹深度顯著增大。

④不同壁厚對應的較優邊長不同,壁厚越厚,較優邊長越小。

為分析圖5中曲線變化的原因,圖6給出了T60-3.5、T77-3.5、T95-3.5、T112-3.5和T132-3.5距迎彈面75 mm截面處鋼管角部內壁典型單元的等效應力σ-時程曲線。

由圖6可知:當外徑小于95 mm時,鋼管角部的等效應力基本相同,可能達到了鋼管的動屈服應力,隨著靶徑減小,混凝土的自約束作用減弱,侵徹阻力減小,因此侵徹深度增大;當靶徑大于95 mm時,隨著外徑的增大,理論上混凝土自約束作用增大,但鋼管角部的等效應力減小,即鋼管的約束作用減小的幅值大于混凝土自約束作用的增大幅值,因此侵徹深度也增大。

2.2.2 壁厚的影響

理論上可以認為,當混凝土的等效半徑相同時,混凝土的自約束作用相同。圖7給出了混凝土等效直徑為60 mm時侵徹深度隨鋼管壁厚的變化關系。

由圖7可知,隨著鋼管壁厚的增大,侵徹深度減小;但是,當鋼管壁厚增大一定程度后(10 mm),增大壁厚對侵徹深度的影響甚微。這表明,鋼管壁厚很大時,未充分發揮鋼管的約束效能。

圖8分別給出了T75-2.5、T77-3.5、T83-6、T92-10和T104-15距迎彈面75 mm截面處鋼管角部內壁典型單元的等效應力-時程曲線,以便分析鋼管壁厚對侵徹深度影響的原因。

由表2和圖8可知:當鋼管壁厚較小時(T75和T77),鋼管的等效應力較大,其值應該接近了鋼管的動屈服強度(與圖6中最大應力相當),鋼管的約束效能得到較充分發揮,其中壁厚3.5 mm的鋼管較壁厚2.5 mm鋼管的等效約束剛度大,約束效應好,其侵徹深度也更小;當鋼管壁厚較大時(10 mm和15 mm),鋼管單元的等效應力較小,遠小于動屈服強度,未能充分發揮材料的強度,因此不經濟。

2.2.3 較優匹配

當含鋼率相同時,鋼管壁厚與邊長的不同匹配對多邊形鋼管約束混凝土的抗侵徹性能有影響。圖9給出了表2中含鋼率約為16.3%工況模擬侵徹深度與邊長的關系。由圖9可知,給定含鋼率時,存在較優的鋼管壁厚與邊長匹配方案,此時侵徹深度最小。對于本文計算工況,較優匹配(T95-3.5)為邊長47.5 mm,壁厚3.5 mm。此時,混凝土等效直徑與彈芯直徑比值為10,鋼管邊長與壁厚的比值為13.5。

需指出,鋼管合理匹配應滿足2個方面的基本要求:一是侵徹深度小于半無限靶;二是較經濟,即含鋼率較低。由表1可知:當鋼管壁厚小于3.5 mm(T75-2.5,T68-2.5,T81-3)或混凝土等效直徑與彈芯直徑之比大于17(T161-3.5,T181-3.5,T268-3.5,T354-3.5)時,侵徹深度均大于半無限靶;當鋼管壁厚為3.5 mm,混凝土等效直徑與彈芯直徑之比為6(T60-3.5)時,侵徹深度大于半無限靶。因此,根據鋼管合理匹配的要求,對于本文彈丸,鋼管壁厚應不小于3.5 mm;混凝土有效直徑與彈芯直徑比值應不大于17(壁厚為3.5 mm時,應大于6)。

為了得到較經濟的匹配,對于表2侵徹深度小于半無限靶工況進行分析。用半無限靶與約束混凝土靶侵徹深度的差值ΔH與含鋼率ω的比值作為經濟性指標,即ΔH/ω越大,鋼管約束混凝土靶的效費比越高。表3給出了ΔH>0工況下的計算結果。

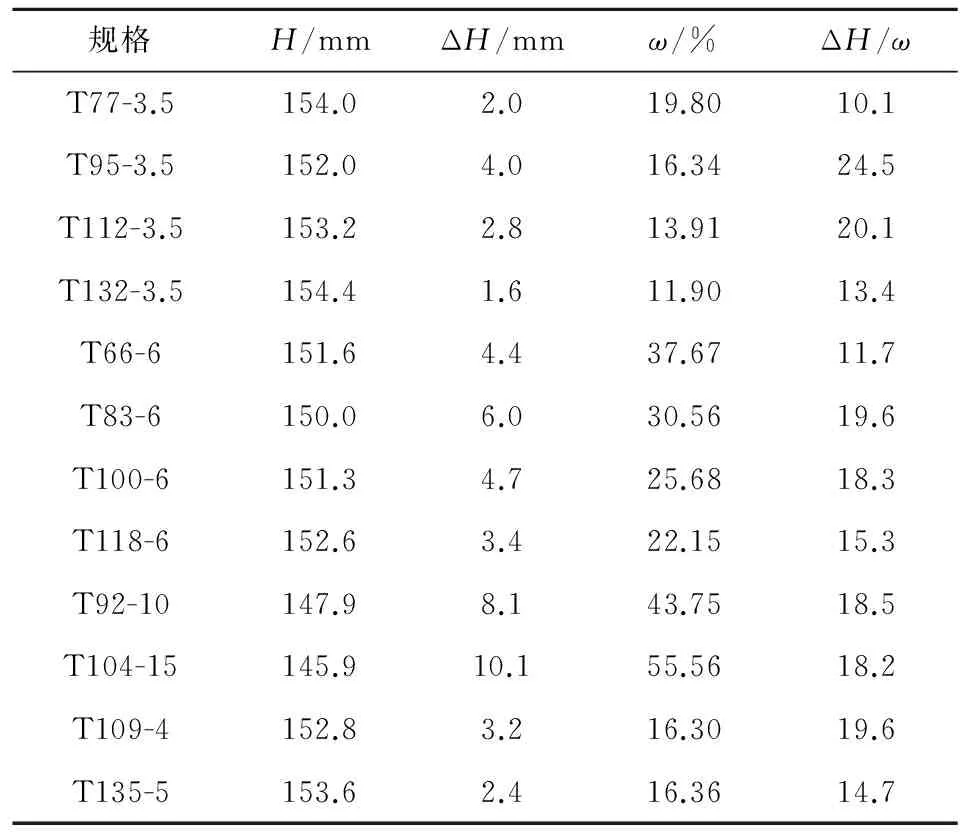
表3 正六邊形鋼管約束混凝土經濟性

由表3可見:

①T95-3.5的ΔH/ω最大,為24.5,為較優匹配,即對于本文彈丸,鋼管的較優匹配為邊長47.5 mm,壁厚3.5 mm。

②T112-3.5、T83-6和T109-4的ΔH/ω較大(約為20),經濟性較好,其鋼管規格可以作為較合理匹配,即:邊長56 mm、壁厚3.5 mm,邊長41.5 mm、壁厚6 mm,邊長54.5 mm、壁厚4 mm。

③T77-3.5、T132-3.5、T66-6和T135-5的ΔH/ω較小(小于15),經濟性較差,其鋼管匹配不好,不宜采用。

綜上所述,正六邊形鋼管約束混凝土的合理匹配:混凝土有效直徑與彈芯直徑比值為6～17;邊長與壁厚的比值不宜大于20,且壁厚不小于3.5 mm。對于本文彈丸,正六邊形鋼管的較優匹配:邊長約47.5 mm,壁厚3.5 mm。

3 結束語

通過對侵徹試驗典型工況進行模擬,驗證了模擬方法和材料模型參數用于模擬本試驗的合理性。

分析了邊長和壁厚的匹配關系對正六邊形鋼管約束混凝土靶抗侵徹性能的影響,表明鋼管壁厚和邊長是影響正六邊形鋼管約束混凝土靶抗侵徹性能的重要因素。

通過優化鋼管邊長與壁厚的匹配,可以得到良好的抗侵徹能力。對于本文彈丸,正六邊形鋼管約束混凝土靶較優的匹配方案建議為:邊長47.5 mm,壁厚3.5 mm。

[1] 甄明,蔣志剛,萬帆,等.鋼管約束混凝土抗侵徹性能試驗[J].國防科技大學學報,2015,37(3):121-127.

ZHEN Ming,JIANG Zhi-gang,WAN Fan,et al.Steel tube confined concrete targets penetration experiments[J].Journal of National University of Defense Technology,2015,37(3):121-127.(in Chinese)

[2] WAN F,JIANG Z G,TAN Q H,et al.Response of steel-tube-confined concrete targets to projectile impact[J].International Journal of Impact Engineering,2016,94:50-59.

[3] 蔣志剛,萬帆,譚清華,等.鋼管約束混凝土抗多發打擊試驗[J].國防科技大學學報,2016,38(3):117-123.

JIANG Zhi-gang,WAN Fan,TAN Qing-hua et al.Mult-hit experiments of steel-tube-confined concrete targets[J].Journal of National University of Defensee Technology,2016,38(3):117-123.(in Chinese)

[4] 蒙朝美.多邊形鋼管約束混凝土靶抗侵徹機理研究[D].長沙:國防科學技術大學,2016.

MENG Chao-mei.Investigation on anti-penetration mechanism of polygonal steel-tube-confined concrete targets[D].Changsha:National University of Defense Technology,2016.(in Chinese)

[5] 王起帆,石少卿,王征,等.蜂窩遮彈層抗彈丸侵徹實驗研究[J].爆炸與沖擊,2016,36(2):253-258.

WANG Qi-fan,SHI Shao-qing,WANG Zheng,et al.Experimental study on penetration-resistance characteristics of honeycomb shelter[J].Explosion and Shock Waves,2016,36(2):253-258.(in Chinese)

[6] 石少卿,王起凡,劉穎芳,等.仿生蜂窩遮彈層抗侵徹機理及數值模擬[J].防護工程,2013,35(4):45-49.

SHI Shao-qing,WANG Qi-fan,LIU Ying-fang,et al.Numerical simulation of anti-penetration characteristics of an alveolate layer[J].Protective Engineering,2013,35(4):45-49.(in Chinese)

[7] 李季,褚召軍,孫建虎,等.鋼管鋼纖維高強混凝土遮彈層抗侵徹數值模擬[J].后勤工程學院學報,2016,32(2):27-31.

LI Ji,CHU Zhao-jun,SUN Jian-hu,et al.Numerical simulation of penetration resistance of shielding layer of steel fiber reinforced high strength concrete filled with steel tube[J].Journal of Logistical Engieering University,2016,32(2):27-31.(in Chinese)

[8] 武珺,王堅茹,陳智剛,等.彈丸對鋼管混凝土結構沖擊效應的數值模擬[J].火力與指揮控制,2013,38(4):107-110.

WU Jun,WANG Jian-ru,CHEN Zhi-gang,et al.Simulation study of projectile impact effect on concrete-filled tube structure[J].Fire Control & Command Control,2013,38(4):107-110.(in Chinese)

[9] 蔣志剛,甄明,劉飛,等.鋼管約束混凝土抗侵徹機理的數值模擬[J].振動與沖擊,2015,34(11):1-6.

JIANG Zhi-gang,ZHEN Ming,LIU Fei,et al.Simulation of anti-penetration mechanism of steel tube confined concrete[J].Journal of Vibration and Shock,2015,34(11):1-6.(in Chinese)

NumericalSimulationofAnti-penetrationPerformanceforHexagonalSteel-tube-confinedConcreteTarget

MENG Chao-mei1,2,JIANG Zhi-gang2,CAI Liang-cai1,LIU Fei2,TAN Qing-hua2

(1.Airfield Engineering Department,Air Force Engineering University,Xi’an 710038,China;2.College of Basic Education,National University of Defense Technology,Changsha 410072,China)

Hexagonal-steel-tube-confined concrete(HSTCC)target has good anti-penetration performance,and it is convenient for engineering application.The influences of edge length and thickness of hexagonal steel tube on anti-penetration performance of HSTCC targets were analyzed by ANSYS/LS-DYNA based on the penetration test of 12.7 mm armor-piercing projectile.In view of cost-efficiency ratio,the economic performance of HSTCC target was analyzed.The results show that it can improve anti-penetration performance of HSTCC targets to enlarge the thickness and reduce edge length of steel tube.And it can get good anti-penetration and economic performance of HSTCC targets to optimize the matching of thickness and edge length of tube.The good matching is edge length with 47.5 mm and thickness with 3.5 mm for the projectile.The results offer reference for designing protective structure of steel-tube-confined concrete.

protective structure;confined concrete;anti-penetration performance;numerical simulation

TV331

A

1004-499X(2017)04-0064-06

2017-09-06

國家自然科學基金項目(51308539)

蒙朝美(1990- ),男,博士研究生,研究方向為結構防護。E-mail:neu_mengchaomei@163.com。