非差觀測模型的BDS靜態精密單點定位算法

楊 虎，徐愛功，祝會忠，馬天明

(遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000)

非差觀測模型的BDS靜態精密單點定位算法

楊 虎，徐愛功，祝會忠，馬天明

(遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000)

為了進一步縮短BDS靜態精密單點定位的收斂時間、提高定位精度，研究BDS精密單點定位的數學模型、各項誤差改正和估計方法，采用非差觀測模型、消電離層組合對非差參數進行估計，改正對流層延遲、相位偏差等各項誤差，并對BDS系統下的可視衛星數、PDOP值、收斂時間及定位精度進行分析。實驗結果表明：BDS靜態精密單點定位水平方向的精度優于2 cm，高程方向優于5 cm；與GPS精密單點定位類似，E方向上定位精度較N方向稍差。

BDS；精密單點定位；收斂時間；定位精度

0 引言

精密單點定位(precise point positioning，PPP)利用國際全球衛星導航系統服務組織(International GNSS Service，IGS)提供的精密衛星軌道和鐘差，處理單臺接收機的非差偽距和載波相位觀測值，估計測站3維坐標、接收機鐘差和對流層延遲等參數，同時利用精細的改正模型改正定位過程中出現的各種誤差，以確定單臺接收機在國際地球參考框架(international terrestrial reference frame，ITRF)坐標系下的坐標，在全球范圍內可實現高精度的定位與測時[1]。精密單點定位(precise point positioning，PPP)突破了相對定位中的距離限制，利用單臺全球衛星導航系統(global navigation satellite system，GNSS)接收機在全球范圍內進行靜態或動態作業，可直接獲得在ITRF框架下dm級至cm級的實時動態導航定位結果和mm級的靜態定位結果，已廣泛應用于測繪、航空、氣象、科學考察和衛星定軌等諸多領域。

北斗衛星導航系統(BeiDou navigation satellite system，BDS)是中國正在實施的自主發展、獨立運行的全球衛星導航系統[2]。截至2012-12-28，BDS已有5顆地球靜止軌道(geostationary Earth orbit，GEO)、5顆傾斜地球同步軌道(inclined geo-synchronous orbits，IGSO)和4顆中圓地球軌道(medium Earth orbit，MEO)衛星在軌運行，初步形成了亞太地區的導航定位服務能力。隨著BDS的逐步完善和發展，基于BDS的PPP技術吸引了國內外學者的廣泛關注。文獻[3]采用實測數據和我國自主研制的精密數據處理軟件PANDA，實現了BDS靜態PPP，定位結果精度達到cm級。文獻[4]利用北京站和武漢站一個星期的觀測數據進行了BDS的靜態試驗，得到了精度1～2 cm的BDS靜態解。文獻[5]也取得了BDS靜態PPP水平方向1～2 cm、垂直方向3～4 cm的定位精度。

本文提出基于非差的BDS多頻PPP算法，采用非差觀測模型、消電離層組合，對對流層延遲、相位偏差等各項誤差進行模型改正和參數估計，計算BDS靜態PPP定位結果，最后進行精度分析與評價。

1 BDS PPP數學模型

1.1 多頻PPP觀測方程

與全球定位系統(global positioning system，GPS)PPP類似，BDS PPP的基本觀測方程采用多頻無電離層組合以消除電離層一階項誤差的影響。BDS具有B1、B2、B3共3個信號頻率，采用B1、B2頻率上的相位和偽距觀測值進行無電離層組合，其具體觀測方程[6]為：

(1)

(2)

1.2 誤差改正策略

通過無電離層組合消除電離層延遲一階項的影響后，PPP的待估參數包括測站坐標、接收機鐘差、天頂對流層延遲，以及各衛星連續觀測弧段內的模糊度參數[7]。采用非差處理模式，數據預處理采用單站數據預處理方法，盡可能地探測與修復周跳并采用參數消去法剔除異常值[8]；對未修復的周跳引入新的模糊度參數，對未探測的周跳與粗差觀測值，在估計模塊的質量控制中進行處理；考慮盡可能多的改正項，對未能精確模型化的誤差因素，通過參數估計吸收；參數估計模塊采用最小二乘估計器，逐個歷元建立觀測方程[9]。具體的參數估計策略如表1所示。

表1 參數估計及其策略

2 BDS PPP誤差改正模型

PPP的誤差改正模型包括與衛星有關的誤差、與傳播路徑有關的誤差和與接收機有關的誤差[10]。針對表1列出的誤差參數，介紹主要的PPP誤差改正項。

2.1 天線相位纏繞

天線相位纏繞是指衛星或接收機天線繞豎軸旋轉時，引起的載波相位觀測值發生變化的現象。GNSS右旋極化方式的衛星信號使得載波相位觀測值與衛星和接收機天線的朝向有關。

在靜態模式下，接收機天線不發生旋轉，不存在天線相位纏繞的影響；但是對于GNSS PPP，無法有效消除衛星天線相位纏繞的影響，其誤差可達到dm級：因此必須對其進行改正。相位纏繞改正公式可表示為

Δφ=2Nπ+Δφ。

(3)

式中：

(4)

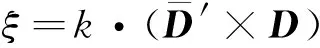
(5)

D=x-k(k·x)+k×y；

(6)

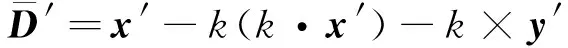
(7)

N=nint[(Δφprev-Δφ)/2π]。

(8)

2.2 固體潮汐

地球固體潮是指在攝動天體(太陽和月球)的萬有引力作用下，使固體地球表面產生周期性的漲落而發生形變的現象。使用長時間觀測的方法僅可以消除大部分周期項的影響，長期項和殘余的周期項影響仍然存在，在徑向方向可達12 cm，水平方向可達5 cm。對于單測站的PPP來說，由于是直接求解測站坐標，若要獲得高精度的定位結果，必須利用模型對固體潮進行改正。固體潮對測站位置影響的近似公式可表示為

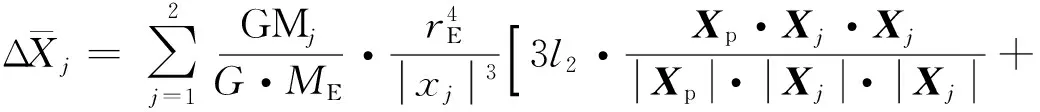
(9)

式中：rE為地球半徑；Xj和Xp分別表示攝動天體(太陽、月球)和測站在地心參考框架中的坐標向量；G為地球引力參數；ME為地球總質量；GMj為攝動天體(j=1表示月球，j=2表示太陽)的引力參數；h2、l2為Love和Shida數(h2=0.609，l2=0.0852)；φ、λ分別為測站的緯度和經度(東為正)；θ為格林尼治平恒星日。

2.3 相對論效應

相對論效應是指由于接收機和衛星鐘所處的狀態不同而引起2臺鐘之間產生相對鐘誤差的現象。GNSS接收機鐘比衛星鐘走得慢，每秒相差0.45 ms左右。為了消除相對論相應的影響，在GNSS衛星發射之前，將其鐘的標準頻率減小約0.004 5 MHz；但是由于受衛星軌道高度變化、地球自轉運動和地球重力場變化等影響，相對論效應改正數并非常數。經過上述改正后，使用精密星歷進行PPP解算時，其殘余誤差引起的測距誤差可表示為

(10)

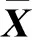
2.4 地球自轉

GNSS定位采用的是與地球一起轉動的協議地球坐標系，若某一時刻衛星從該瞬時空間位置向地面發射信號，當衛星信號到達地面接收機時，與地球固連的協議地球坐標系相對于衛星信號發射瞬間的位置已產生了旋轉(繞Z軸旋轉)。此時，計算衛星位置時必須考慮到地球旋轉改正，若取ω為地球的自傳角速度，則旋轉的角度為

(11)

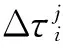
(12)

式中(Xj，Yj，Zj)為衛星瞬時坐標。

2.5 對流層延遲

對流層是無線電波傳播的隨機不均勻介質，電磁波通過對流層時由于傳播速度的變化以及傳播路徑彎曲而產生延遲。對流層延遲分為干延遲和濕延遲。文獻[10]指出對流層延遲的大小對收斂速度的影響非常明顯，因此對流層延遲的改正是必不可少的。

將根據大量的長期觀測得到的氣象資料用解析的方法，以地表的氣象參數近似反演天頂方向上的氣象時空變化，建立中性大氣天頂延遲模型，并建立相應的投影函數，將傳播路徑上的對流層延遲映射到天頂方向，便于對流層延遲的參數化。

對于對流層干延遲，采用Saastamoinen模型進行改正，其公式為

(13)

式中：Ps為地面氣壓(mbar)；Ts為地面溫度(℃)；es為地面水氣壓(mbar)；rh為相對濕度；f(φ，h)為地球自轉所引起重力加速度變化的修正，φ為測站的地心緯度(°)，h為測站高程(km)；ΔDz，trop為天頂總對流層延遲；ΔDz，dry、ΔDz，wet分別為天頂對流層干延遲與濕延遲。

一般情況下，對流層延遲的干分量幾乎能得到完全改正。而對于濕分量，由于大氣層中水汽分布在時間和空間上變化的隨機和復雜性，利用地面氣象資料很難模擬上層空間的水汽變化；模型改正后的對流層延遲殘余影響還是在cm量級，這部分殘差一般利用一階高斯-馬爾可夫或隨機游走過程進行估計[2]。GMF投影函數由于篇幅限制，不作詳細介紹，可參看文獻[2]。

隨機游走模型是非平穩的隨機過程，隨機游走過程的方差隨時間而變化。隨機游走過程的計算方法為

(14)

其離散化方程為

(15)

式中：ρ(t)為t時刻隨機游走模型的方差；w(t)為方差的零均值白噪聲；Δt為時間間隔。

2.6 天線相位偏差

天線相位偏差包含兩方面的內容：一方面是由天線平均相位中心與天線幾何中心不一致所產生的平均相位中心偏差(phase center offset，PCO)；另一方面是由觀測時刻的瞬時天線相位中心與平均相位中心不一致所產生的天線平均相位中心變化(phase center variations，PCV)。天線相位中心偏差隨著衛星信號輸入的強度與方向而變化，其值可達數mm到數cm。

由于目前IGS只提供了粗略的BDS衛星端PCO改正，尚無機構或組織提供BDS衛星端PCV以及接收機端的PCO與PCV信息；因此無法進行精確的天線相位中心偏差及其變化改正[7]。

3 實驗與結果分析

為了評定BDS PPP的定位性能，選取了8個測站2016年DOY101—107共7 d的BDS雙系統的GNSS觀測數據進行靜態PPP試驗。試驗數據來源于IGS的MGEX(muti-GNSS experiment)觀測網，所選測站信息如表2所示。CMUM、CPNM、EUSM均分布在亞洲南部，CUT0站位于澳大利亞的Curtin大學內，DAE2、GMSD分別位于韓國與日本，HARB站位于南非，NRMG位于大洋洲中部。

觀測數據采樣間隔為30 s，截至高度角7°，精密產品采用IGS提供的BDS 30 s精密星歷和30 s鐘差產品。為比較分析，對各測站同時進行GPS PPP解算，并與該站準確值進行對比。

實驗解算各測站24 h的觀測數據，將解算結果與準確值做差，獲得E、N、U共3個方向上的坐標偏差以分析BDS PPP的收斂時間和定位精度。

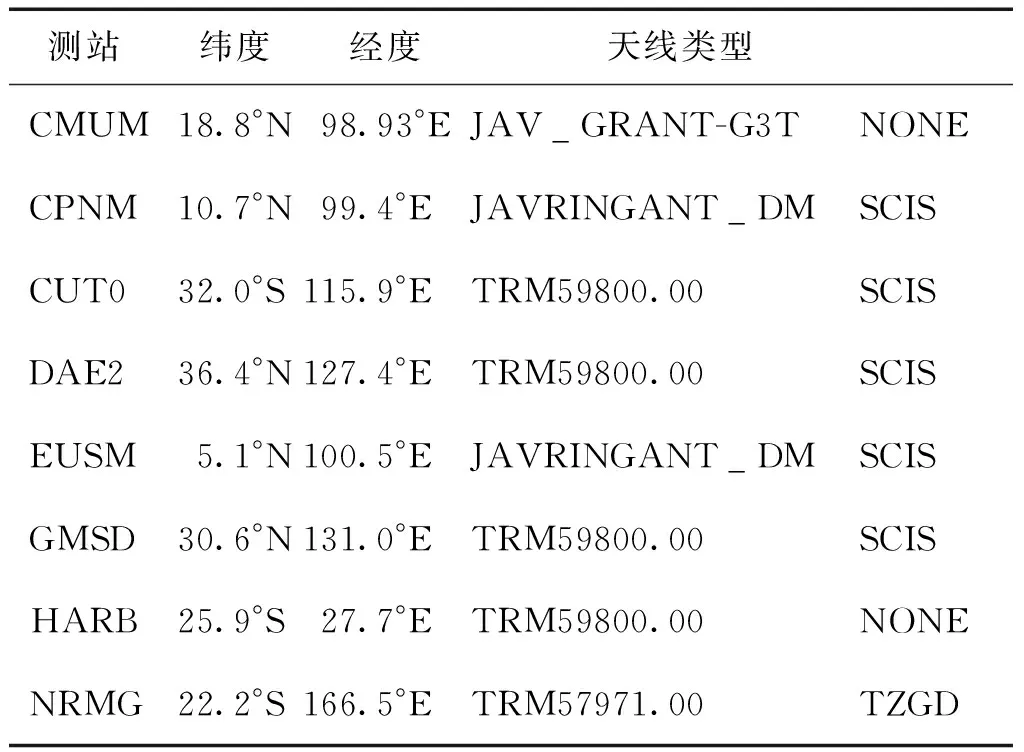
表2 測站相關信息

3.1 收斂速度分析

收斂的判斷依據定義為E、N、U各向定位偏差均優于1 dm。為確保結果的可靠性，同時檢查了首次收斂時刻后20個歷元的位置偏差，只有當連續20個歷元的偏差都在限值以內，才認為當前歷元的定位結果收斂。

以DOY101 CUT0站單天的定位結果為例，比較分析了BDS/GPS PPP的定位偏差序列，如圖1所示。

從圖1中可以看出，BDS靜態PPP經過50 min可以收斂，而GPS靜態PPP收斂時間相對較短，約30 min。

圖2為該時段BDS、GPS PPP的位置精度衰減因子(position dilution of precision，PDOP)值和可視衛星數。

從圖中可以看出：盡管大部分時間BDS衛星數多于GPS，但由于目前BDS的MEO衛星數較少，總體圖形結構變化不如GPS星座顯著；而且由于當前BDS的跟蹤站數量有限，BDS的精密軌道精度較低，導致BDS PPP的收斂時間長于GPS。

對各天數據的靜態PPP收斂時間進行統計，得到各天的平均收斂時間，結果如圖3所示。

從圖3中可以看出：對基于BDS、GPS系統的PPP定位，各天之間的平均收斂具有良好的一致性，天與天之間并無明顯差異；BDS平均收斂時間均在60 min以上，而GPS平均收斂時間均小于40 min。所有數據的收斂時間統計如下：BDS靜態PPP的平均收斂時間為77.7 min；GPS靜態PPP的平均收斂時間為32.6 min。

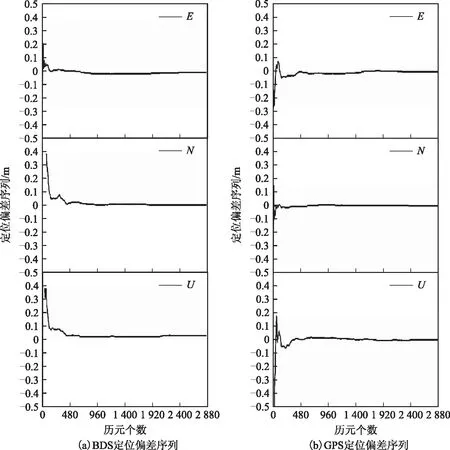
圖1 DOY101 CUT0站單天BDS、GPS靜態PPP定位偏差序列

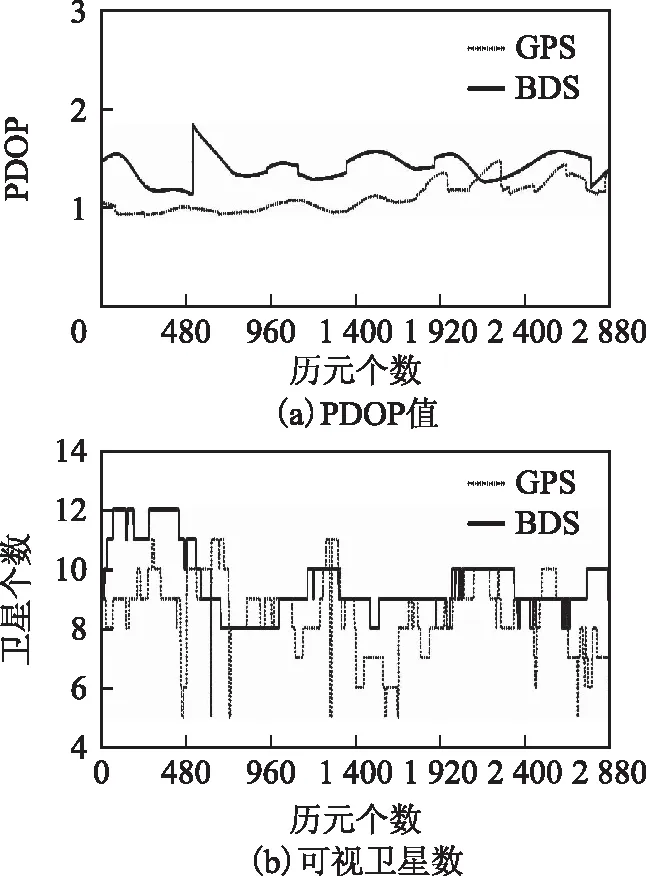
圖2 DOY101 CUT0站單天BDS、GPSPDOP值和衛星數

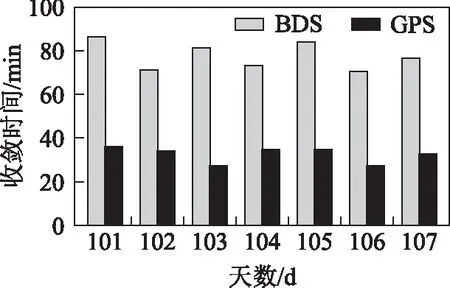
圖3 DOY101-107各天靜態PPP平均收斂時間

眾所周知，PPP的定位結果受衛星軌道和鐘差產品精度、星座幾何強度的影響較為明顯。目前，BDS的精密衛星產品的精度較GPS差，且無法精確改正PCO和PCV誤差[7]；而且，BDS的可用衛星數只有23顆，而GPS有31顆，其幾何強度遠比BDS好：因此，當前條件下BDS PPP的收斂時間明顯長于GPS PPP。

3.2 BDS/GPS定位精度分析

為了定量分析收斂后BDS PPP的定位精度及穩定性，對每天的解算結果進行統計，計算其定位偏差的均方根(root mean square，RMS)。以DOY101為例，表3中給出了各測站單天解的RMS值。

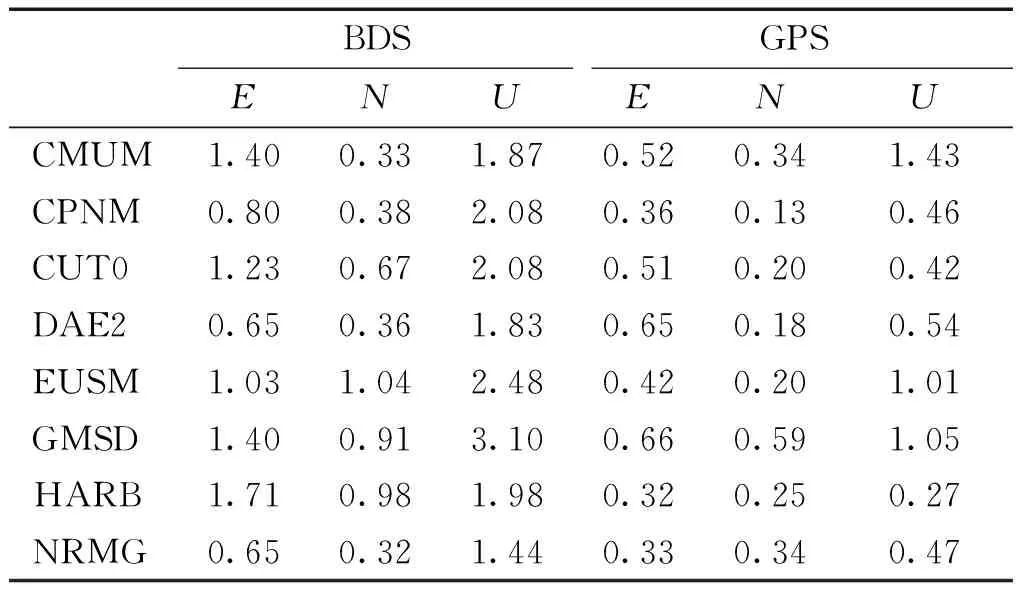
表3 各站單天解E、N、U方向上的RMS值 cm

從表中可以看出，BDS靜態PPP單天解水平方向精度優于2 cm，高程方向優于5 cm；GPS靜態PPP水平與高程方向精度分別優于1 cm、2 cm。整體而言，BDS PPP收斂后的定位精度要略低于GPS PPP；這主要是由于當前BDS的MEO衛星數較少，衛星分布及定位的幾何圖形結構比GPS差，且軌道和鐘差產品精度相對較低而導致的。從圖中可明顯看出，2種PPPN方向定位精度均優于E方向，這是由于PPP保留浮點解，未將模糊度參數固定為整數的緣故[9]。

4 結束語

本文利用IGS發布的BDS精密星歷和鐘差文件，編程實現了BDS 靜態PPP算法，采用IGS站提供的8個測站7 d的數據進行實驗，并以準確值作為參考進行對比。結果表明：1)BDS靜態PPP由于可視衛星數、地面跟蹤站數量較少以及精密產品精度較低的影響，收斂時間長于GPS 靜態PPP，約為80 min；2)BDS靜態PPP單天解定位精度水平方向優于2 cm，高程方向優于5 cm，相比于GPS靜態PPP水平1 cm、高程2 cm的精度相差不多，可以認為目前BDS在區域的PPP性能與GPS相當。隨著BDS星座的擴建、地面跟蹤站的增多，以及精密產品精度的提高，其收斂時間和定位精度將得到進一步提高。

[1] 周承松，彭月，張小紅，等.精密單點定位收斂時間的確定方法研究[J].導航定位學報，2016，4(1)：80-87.

[2] 徐宗秋.基于多導航衛星系統的精密單點定位模型與方法研究[D].阜新：遼寧工程技術大學，2013.

[3] 施闖，趙齊樂，李敏，等.北斗衛星導航系統的精密定軌與定位研究[J].中國科學：地球科學，2012，42(6)：854-861.

[4] 馬瑞，施闖.基于北斗衛星導航系統的精密單點定位研究[J].導航定位學報，2013，1(2)：7-10.

[5] 王閱兵，游新兆，金紅林，等.北斗導航系統與GPS精密單點定位精度的對比分析[J].大地測量與地球動力學，2014，34(4)：110-115.

[6] 鮑建寬，陳偉榮，高成發.精密單點定位的數學模型選擇[J].黑龍江工程學院學報(自然科學版)，2013，27(2)：1-4，7.

[7] 張小紅，左翔，李盼，等.BDS/GPS精密單點定位收斂時間與定位精度比較[J].測繪學報，2015，44(3)：250-255.

[8] 張寶成，歐吉坤，袁運斌，等.基于GPS多頻原始觀測值的精密單點定位算法及應用[J].測繪學報，2010，39(5)：478-483.

[9] 涂銳，黃觀文，凌晴.GPS單頻精密單點定位的研究發現[J].測繪科學，2011，36(3)：68-70.

[10] 曹相，高成發.GPS精密單點定位(靜態)影響收斂速度的因素分析[J].現代測繪，2007，30(1)：19-21.

BDSstaticprecisepointpositioningalgorithmbasedonnon-differenceobservationmodel

YANGHu，XUAigong，ZHUHuizhong，MATianming

(School of Geomantics，Liaoning Technical University，Fuxin，Liaoning 123000，China)

In order to improve the the convergence time and positioning accuracy of BDS static precision point positioning，the paper studied on the mathematical models of BDS precise point positioning and the methods of error correction and estimation，used tnon-difference observation model，ionosphere combination to estimate the non-difference parameters and correct the errors of troposphere delay，phase deviation and so on.Then the visible satellites，PDOP values，convergence time and positioning accuracy of BDS system were analyzed.Experimental result showed that the accuracy of horizontal direction of BDS static precision point positioning could be better than 2 cm，and that of elevation direction could be better than 5 cm；moreover，similar with GPS precision point positioning，the accuracy of BDS static precision point positioning in the east would be worse than that in the north.

BDS；precision point positioning；convergence time；positioning accuracy

2016-12-12

國家重點研發計劃項目(2016YFC0803102)；遼寧省高等學校創新團隊項目(LT2015013)。

楊虎(1992—)，男，安徽阜陽人，碩士研究生，研究方向為GNSS高精度定位。

楊虎，徐愛功，祝會忠，等.非差觀測模型的BDS靜態精密單點定位算法[J].導航定位學報，2017，5(4)：86-91.(YANG Hu，XU Aigong，ZHU Huizhong，et al.BDS static precise point positioning algorithm based on non-difference observation model[J].Journal of Navigation and Positioning，2017，5(4)：86-91.)

10.16547/j.cnki.10-1096.20170416.

P228

A

2095-4999(2017)04-0086-06