基于動態獎懲的分支策略的SAT完備算法

劉燕麗，徐振興，熊 丹

(1.武漢科技大學 理學院，武漢 430081； 2.華中科技大學 計算機科學與技術學院，武漢 430074)

基于動態獎懲的分支策略的SAT完備算法

劉燕麗1,2*，徐振興2，熊 丹1

(1.武漢科技大學 理學院，武漢 430081； 2.華中科技大學 計算機科學與技術學院，武漢 430074)

針對學習子句數量有限或相似度高導致歷史信息有限、搜索樹不平衡的問題，提出了基于動態獎懲的分支策略。首先，對每次單子句傳播的變元進行懲罰，依據變元是否產生沖突和產生沖突的間隔，確立不同的懲罰函數;其次，在學習階段，利用學習子句確定對構造沖突有益的變元，非線性增加它們的活躍度;最后，選擇活躍度最大的變元作為新分支變元。在glucose3.0算法基礎上，完成了改進的動態獎懲算法——AP7。實驗結果表明，相比glucose3.0算法，AP7算法的剪枝率提高了14.2%～29.3%，少數算例剪枝率的提高可達51%，且改進后的AP7算法相比glucose3.0算法，運行時間縮短了7%以上。所提分支策略可以有效降低搜索樹規模，使搜索樹更加平衡，減少計算時間。

NP完全問題；可滿足性問題；沖突驅動子句學習；完備算法；分支策略

0 引言

可滿足性問題(SATisfiability problem, SAT)是計算機科學領域經典的NP問題(Non-deterministic Polynomial Complete problem, NPC)，在計算機科學理論中占有非常重要的地位。現實世界的問題大多數都是NP問題，即不確定性問題。比如，超大規模集成電路測試、資源配置、網絡的搜索、數據挖掘、城市交通等，解決這些工業問題的SAT技術推動了人工智能的重要發展。

目前，絕大多數SAT完備算法是基于深度遍歷二叉樹的DPLL(Davis Putnam Logemann Loveland)[1]算法。2001年Moskewicz等[2]提出的沖突驅動子句學習(Conflict Driven Clause Learning, CDCL)，使得SAT求解效率有了標志性的進步，在合理時間內，求解規模從數百個變元，擴大到數萬個變元。后續提出的SAT完備算法的主要方法和改進[3-4]均基于沖突驅動子句學習技術。比如，非時間序列回溯(Non-chronological Backtracking, NCB)[5]，該策略分析沖突的產生原因，記錄優化的學習子句，并在回溯后，優先滿足學習子句，以避免再次陷入相同沖突。文字塊距離(Literal Block Distance, LBD)[6]是統計學習子句中不同分支層的變元數，是一個動態變化值。子句庫始終保留二元學習子句或LBD值小的學習子句。該策略既避免了因學習子句劇增而內存崩潰的危險，又保留了質量高的變元約束條件，是有效的子句刪除策略。

變元獨立衰減 (Variables State Independent Decaying Sum, VSIDS)[7]分支策略強化了沖突學習對搜索的影響。一旦變元在產生學習子句的過程中出現，那么該變元的活躍度將非線性增加。近幾年的SAT競賽數據顯示變元獨立衰減策略或者其變種是較為高效的分支策略。動態重啟(Dynamic Restart, DR)[8]是當算法較長時間不能找到沖突時，程序撤銷之前的搜索動作，重新開始遍歷二叉樹。因為新搜索是在含有學習子句的子句庫中進行，學習子句代表了之前的搜索信息，所以重啟并不是推翻之前的搜索。目前，工業算例的規模可達百萬個變元數，千萬個子句數。因為問題的復雜度高，量化這些策略在搜索過程中的作用，以及它們之間的相互影響，是非常困難的事情。

本文針對在搜索空間為2n(n是變元數)的二叉樹中，由于學習子句數量有限，或學習子句相似度高而導致搜索樹層次過深、計算效率低的問題，提出了雙階段評分的新分支策略。即對于搜索階段傳播的變元，若其對構造沖突作用小，則給予適當的懲罰；對于學習階段中構建沖突的變元給予獎勵，通過較為全面地評估變元對搜索的影響，以達到更快地發現沖突，提高剪枝率的目標。計算了SAT國際競賽的工業組算例，實驗結果表明新變元選擇策略可有效地調整搜索樹的高度，縮短運算時間。

1 可滿足性問題的求解

文獻[9]給出了可滿足性問題的相關術語的定義。

1.1 相關術語

定義2 子句集。子句是V上若干文字的析取，記為c。子句集是由若干子句構成的集合，記為C。子句長度是子句所含文字的個數，記為|c|。特別地，長度為1的子句稱為單子句。長度為0的子句稱為空子句，記為δ。

定義3 子句滿足。若子句滿足當且僅當子句中至少有1個文字為true。因不含有任何文字，所以空子句永遠不滿足。若子句不滿足當且僅當子句中所有文字均為false，該子句又稱為沖突子句，記為□。

定義4 合取范式。 合取范式(Conjunctive Normal Formula, CNF)是由若干V上的子句合取構成的命題公式，記為F。

定義5 真值指派。 真值指派是命題變元V′→{1,0}的映射，V′?V，記為A。當V′=V時，A是完整真值指派；否則，稱之為部分真值指派。

定義6 沖突集。 對任意一組V上的真值指派，若子句集C中至少含有1個不滿足子句，則稱C為沖突集，記為Φ。若兩個沖突集的交為空，則稱它們是相互獨立的。

定義7 SAT問題。 對于命題變元集合V和子句集C，判定是否存在一組關于V的真值指派使得C中所有子句滿足。

1.2 SAT問題的完備算法

目前，DPLL是絕大多數SAT完備算法的主流程的控制程序。算法從根節點開始深度遍歷二叉樹，當遇到沖突的真值指派時，算法回溯。若算法找到一組真值指派，使得每個子句滿足，那么程序終止，返回“可滿足”。若遍歷完完整的二叉樹后，未找到一組真值指派使得所有子句滿足，那么程序終止，返回“不可滿足”。DPLL算法詳見文獻[1]。

1)測試沖突的單子句傳播。

單子句傳播(Unit Propagation)[9-10]可以幫助SAT算法推導出真值指派的沖突，減少搜索空間。算法1是單子句傳播的具體過程。

算法1 UnitPropagate(F)。

輸入 合取范式F；

輸出 若有沖突，返回沖突子句，否則返回NoConflict。

1)

F′←F

2)

do {

3)

取UnitQue中單子句cj，滿足cj的文字l；

4)

形如l∨li…∨lk的子句已滿足，從F′中移除；

5)

6)

if (lm∨ls…∨lt為單子句)

7)

lm∨ls…∨lt入UnitQue隊列；

8)

else if (lm∨ls…∨lt為空子句)

9)

returncn；

10)

}while(UnitQue不為空)

11)

return NoConflict

圖1 F的邏輯蘊含圖Fig. 1 Logical implication graph of F

2)學習子句的產生。

當搜索到沖突后，SAT算法進入分析沖突的原因，產生學習子句的學習階段。圖2顯示了由沖突子句出發，通過消解規則，逐一產生學習子句的過程。消解規則是若兩個子句中包含有相反文字，則將這對文字刪除，剩余文字通過析取構成新的子句。消解規則不改變合取范式的滿足性。

圖2 學習子句的產生過程Fig. 2 Generation process of learning clauses

2 基于動態獎懲分支策略的SAT算法

DPLL+子句學習是SAT完備算法的基礎。為了減少搜索樹的節點數，提高算法的效率，分支策略將選擇對搜索樹規模影響大的變元。

2.1 基于學習過程的變元策略

如變元獨立衰減策略或其變種，這類基于學習過程的分支策略是在產生學習子句的學習階段，對參與消解操作的所有子句包含的變元，增大其活躍度。算法始終選擇當前活躍度最大的變元作為新的分支點。如例1會增加變元x5、x9、x11、x23、x2、x15的活躍度。變元參與構造沖突越多，其活躍度越大。在后續搜索中選擇活躍度大的變元，易找到之前發現過的沖突，有利于減少搜索路徑。

我們發現僅基于學習過程的分支策略對減小搜索樹規模并不總是有效的。某些情況下，相似的學習過程導致學習子句相似度高。學習子句代表的搜索的歷史信息比較集中，回溯后或重啟后，基于學習過程的變元策略會僅有少量變元可以優先選擇。搜索沒有足夠的歷史信息指引方向，會隨機去選擇變元作為新的分支節點，這會導致搜索樹層次過深，算法陷入困境。目前，絕大多數SAT求解器采用動態重啟逃脫這種困境。因為子句庫保存了表述沖突關系的學習子句，所以重啟后的搜索與沒有學習信息的原始搜索不同。通過優先選擇沖突關系多的變元，新搜索可能會找到沖突。但是動態重啟只能緩和算法遇到的問題，并未改變變元的活躍度，程序可能會又陷入到某一子樹的過度搜索中。

2.2 基于學習與搜索雙階段的分支策略

為了減少搜索樹規模，使搜索樹更加平衡，全面地評估變元對搜索的作用，使得越容易構造沖突的變元，越接近樹根，增大搜索優先找到沖突的概率是基于動態獎懲分支策略的獎懲算法——AP7(Award and Punishment 7)的主要改進思路。

SAT完備算法包括2個主要過程：一是搜索過程，即單子句傳播，發現沖突的操作；二是學習過程，即產生學習子句，增加沖突變元的活躍度，確定回溯層次。AP7算法對以上兩個過程中的變元進行全面的評估。在搜索階段，降低較長時間內未找到沖突的變元的活躍度，在學習階段，提高對構造沖突有益的變元的活躍度，并優先選擇當前活躍度最大的變元作為分支變元。算法流程如圖3所示。

算法2是AP7的偽代碼。算法中penalty是讓變元活躍度隨著傳播而衰減的獨立參數；numCC是沖突數，初始值為0；penaltyV是存儲待懲罰變元的數組；dl是搜索樹的層數；lastC[x]是存放變元x的最近一次出現的沖突；Act是記錄變元x活躍度的數組；ΦL是學習子句L對應的沖突集，Variable(ΦL)是沖突集中出現的所有變元的集合；V是輸入算例的變元集合；BranchV是分支變元；max函數返回活躍度最大的變元；bl是SAT算法產生沖突后的回溯層次；AP7采用非時間序列回溯的方法；cancel函數是算法回溯到指定的層次。

圖3 AP7算法流程Fig. 3 AP7 algorithm flowchart

算法2 AP7(F)。

輸入 合取范式F；

輸出F是否滿足，滿足返回“SAT”，不滿足返回“UNSAT”。

1)

penalty=0.6;numCC=0;penaltyV.clear();

2)

for(;;)

3)

UnitPropagate(F)且將傳播的變元x壓入penaltyV中；

4)

forxt∈penaltyVdo

//搜索階段的懲罰

5)

if UnitPropagate(F)==沖突 then

6)

ifpenalty<0.98 then

7)

penalty=penalty+10-7;

8)

end if

9)

Act[xt]=Act[xt]*penalty+(1-penalty)/(numCC-

lastC[xt]);

10)

else

11)

Act[xt]=Act[xt]*penalty;

12)

end if

13)

end for

//結束懲罰計算

14)

penaltyV.clear();

15)

if UnitPropagate(F)==沖突 then

//找到沖突

16)

ifdl==0 then

17)

return "UNSAT";

18)

end if

19)

numCC++;

20)

FUIP方式產生學習子句L,并返回回溯層次bl；

21)

forxi∈Variable(ΦL) do

//學習階段的獎勵

22)

lastC[xi]=numCC;

23)

Act[xi]=Act[xi]+(1/0.9)numCC

24)

ifAct[xi] >1E100 then

25)

forxi∈Vdo

26)

Act[xi]*=1E-100;

//作平滑

27)

end for

28)

end if

29)

end for

//學習階段獎勵結束

30)

cancel(bl);

31)

翻轉學習子句L中未滿足的文字；

32)

else

//未找到沖突

33)

BranchV=max(Act[xk]);xk∈V

34)

if 所有變元都有了真值指派 then

35)

return "SAT";

36)

end if

37)

dl++;

38)

BranchV壓入penaltyV;

39)

end if

40)

end for

AP7首先作單子句傳播，將單子句傳播中所有變元壓入penaltyV中，如果這些變元的真值指派之間沒有沖突，那么將它們的活躍度降低至60%～98%；如果這些變元之間有沖突那么除了適當的給予懲罰之外，還給予少量的獎勵。以上是傳播階段變元的活躍度計算。

如果單子句傳播發現了沖突，且當前搜索層次是第0層，那么SAT問題無解，返回“UNSAT”；如果當前層次不是第0層，則AP7對沖突進行分析，采用FUIP方式產生學習子句，確定回溯層次bl。在學習子句對應的沖突集中出現的變元，其活躍度會得到大小為(1/0.9)numCC的獎勵。AP7對構造沖突的變元進行獎勵后，開始回溯，撤銷第bl+1層到當前層傳播的變元。因為回溯后的學習子句是單子句，所以滿足學習子句，進入到新的一輪單子句傳播。

如果單子句傳播未發現沖突，則AP7選擇活躍度最大且未賦值的變元作為分支變元。分支層次增加1，分支變元壓入penaltyV中。AP7開始新的一輪單子句傳播。如果所有變元具有合理的真值指派，沒有未賦值的變元，那么AP7找到了問題的解，算法返回“SAT”。

學習階段對變元的獎勵值不是固定值，該值隨著搜索層次的加深，獎勵值越大。為了防止活躍度值的溢出，當某個變元的活躍度大于閾值1E100時，變元的活躍度整體地平滑下降。搜索階段實施懲罰時需注意以下幾個問題：1)降低活躍度的penalty不是一個固定值。算法找到越多的沖突，活躍度降低得越少。這是因為最近找到的沖突很大概率上質量會比之前的沖突要好。2)當搜索找到沖突時，增加了一個變量1/(numCC-lastC[xt])。若某個變元一段時間之后，再次找到了沖突，那么它與長時間未有沖突的變元相比，活躍度應該高一些。3)當搜索沒有找到沖突時，直接大幅度降低變元的活躍度。雖然這種方式比較野蠻，但是對于復雜的問題，它是有效的。

3 新分支策略的評估

3.1 實驗環境和設置

為了準確評估新分支策略在求解工業問題上的作用，實驗對比了新算法AP7和glucose3.0。兩者僅分支策略不同，AP7采用的是基于獎懲的新策略，而glucose3.0是基于學習過程的變元獨立衰減分支策略。在SAT競賽的工業組中，glucose算法及其變種[12]有重要的地位。glucose2.3算法是2013年競賽的工業組冠軍，獲得2014年—2016年工業組前三名的算法均是以glucose3.0為基礎的；同時，glucose被SAT組委會用于確定算例的難度等級。

實驗的機器配置采用Intel E5 2.7 GHz處理器、32 GB內存、Centos 6.3服務器版本的操作系統。在相同的機器上，AP7算法和glucose3.0算法求解2016年SAT Competition (http://www.satcompetition.org) 公布的工業算例集。這些算例來自軟件測試、調度、硬件電路測試、網絡安全、加密算法等實際問題。根據算例的解的滿足性，這些算例被分為可滿足算例集和不可滿足算例集。實驗采用SAT競賽的限定時間，每個算例的運算不超過5 000 s，若超出，該算例結果記為unsolved。

3.2 實驗結果

首先給出glucose3.0和AP7算法在相同機器上計算相同算例的時間結果。glucose3.0和AP7算法計算加密安全哈希算法(Secure Hash Algorithm, SHA)、矩形裝配、交通規劃等工業問題的運算時間如表1所示。表1中算例的變元數是13 408～521 147，子句數是308 391～13 378 009。表1顯示，在27個算例中AP7算法有22個算例運行時間少于glucose3.0，AP7算法相比glucose3.0計算可滿足算例的運行總時間縮短了31.66%。

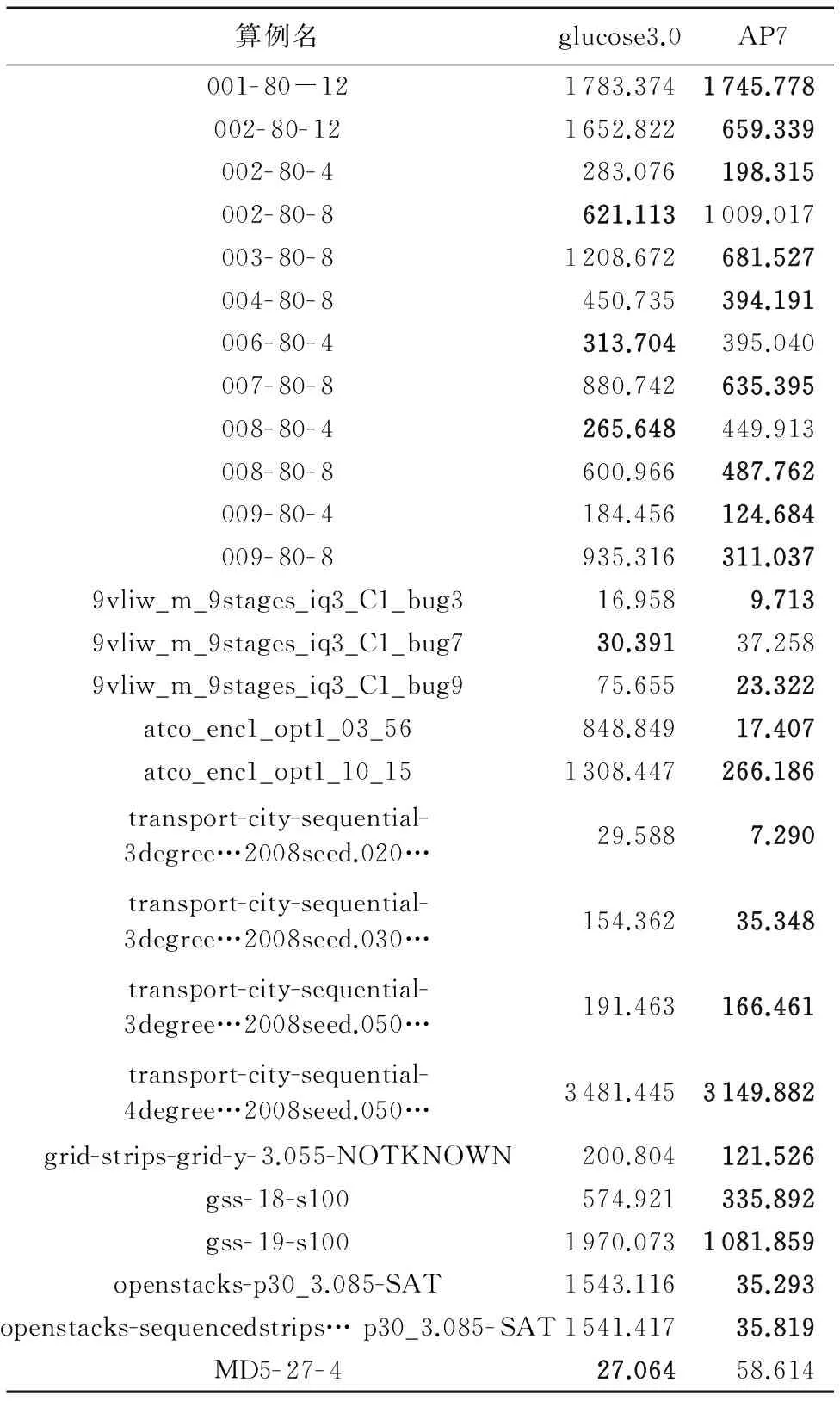
表1 不同算法可滿足算例的運行時間對比 sTab. 1 Running time comparison of SAT examples for different algorithms s

glucose3.0和AP7算法計算硬件電路優化、電子控制等工業問題的運算時間對比如表2所示。表2中算例的變元數是3 295～89 315，子句數是13 079～5 584 002。 glucose3.0在5 000 s限定時間內，未求解出表2的第1個算例smtlib-qfbv-aigs-ext_con_032_008_0256-tseitin，該算例在競賽網站公布的最好成績是Lingeling(druplig)算法的1.432 s。根據表2中AP7和glcuose3.0均計算出結果的21個算例，有17個算例AP7算法運算時間少于glucose3.0，AP7算法的運行總時間比glucose3.0縮短了37.13%。

表2 不同算法不可滿足算例的運行時間對比 sTab.2 Running time comparison of UNSAT examples for different algorithms s

3.3 實驗結果分析

分支數是SAT完備算法效率的核心參數。當搜索樹分支減少，搜索空間減小，SAT完備算法的運算時間才會降低。

glucose3.0和AP7計算的部分算例的分支數以及降低比如表3所示。降低比=(glucose3.0分支數-AP7分支數)/(glucose3.0分支數)。

表3 不同算法算例的分支數對比Tab. 3 Branch number comparison for different algorithms and examples

從表3可以看出，除1個算例外，改進后的AP7相比glucose3.0可降低分支數為14.2%～56.5%。通過表3實驗數據可知基于獎懲的分支策略相比僅增加變元活躍度的分支策略可以有效地減小搜索樹規模。

為了進一步觀察動態獎懲策略對搜索沖突的影響，每增長1萬個沖突時，算法輸出重啟的次數。圖4～5 對比了兩個算法計算相同算例時，相同沖突數下所需的重啟次數。glucose3.0計算002- 80- 12.cnf重啟了103 921次，找到13 841 064次沖突；AP7則重啟了67 927次，找到10 633 140次沖突。圖4顯示在0～10 633 140次沖突時，兩個算法相應的重啟次數。AP7和glucose3.0采用相同的重啟策略。在0～105萬次沖突搜索中，glucose3.0比AP7重啟次數少；在105萬～1 384萬次沖突中，AP7重啟次數少于glucose3.0。實驗結果表明AP7算法綜合地評定變元在搜索中的作用，可有效地減少較長時間找不到沖突的情況，從而減少了重啟次數。

圖4 可滿足002- 80- 12.cnf的重啟次數和沖突數的對比Fig. 4 Comparison of conflicts and restarts of SAT 002- 80- 12.cnf

glucose3.0計算不可滿足算例6s168-opt.cnf的沖突數是2 063 558，重啟次數是4 758；AP7計算該算例的沖突數是1 084 645，重啟次數是2 059。圖5顯示了6s168-opt.cnf在0～120萬次沖突范圍內兩個算法的重啟次數的對比。從圖5可以看出，產生相同個數的沖突時，AP7的重啟次數遠低于glucose3.0算法的重啟次數。因此，基于獎懲的分支策略AP7對于不可滿足的工業問題，也可以有效地減少搜索樹層次，從而減少重啟次數。

圖5 不可滿足6s168-opt.cnf的沖突數和重啟數的對比Fig. 5 Comparison of conflicts and restarts of UNSAT 6s168-opt.cnf

從學習子句質量進一步分析新分支策略的作用。SAT完備算法每次找到1個沖突，產生1個學習子句。每個學習子句會計算其相應的LBD值，LBD值為2的學習子句是指產生沖突的原因子句分布在搜索樹的2個層次。因為LBD值為2的學習子句描述了關系更為緊密的沖突變元之間的關系，所以質量高的這類學習子句一直保留在子句庫中，不會被刪除。表4列出了glucose3.0和AP7算法正確求解的算例的重啟次數，LBD_2學習子句數以及LBD_2學習子句數與重啟次數的比例。若LBD_2學習子句數與重啟次數的比例越大，說明重啟后被選擇的搜索變元關系更加緊密，導致找到沖突后學習子句的LBD值下降。表4顯示在重啟次數較小時(重啟次數<150)glucose3.0算法重啟的平均學習質量較高，但是求解復雜的問題(重啟次數>150)AP7算法的平均學習質量較高。這表明綜合評定變元可以產生更多高質量學習子句。

表4 不同算例的重啟次數、LBD_2子句數的對比Tab. 4 Comparison of number of restarts and LBD_2 clauses for different examples

4 結語

工業問題規模大，求解難度高。學習子句數量少或質量不高對搜索的指導意義有限，使搜索易陷入到層次過高，不平衡的困境中。為了縮短求解問題的時間，算法需要盡可能地選擇對尋找沖突更有利的變元，以使得搜索樹更加平衡。基于動態獎懲的分支策略綜合地評估了變元對傳播和學習兩個主要過程的影響，建立懲罰函數。相比傳統、單一的獎勵變元評估策略，動態獎懲的分支策略通過調整更關鍵的變元靠近根節點，從而有效地降低重啟次數，提高了學習子句質量，減小搜索樹的規模。分支變元策略的改變使得搜索樹更加緊湊，將會影響子句刪除的標準，后續將對學習子句的刪除作新的探索。

References)

[1] DAVIS M, LOGEMANN G, LOVELAND D. A machine program for theorem proving [J]. Communications of the ACM, 1962, 5(7): 394-397.

[2] MOSKEWICZ M W, MADIGAN C F, ZHAO Y, et al. Chaff: engineering an efficient sat solver [C]// Proceedings of the 38th Annual Design Automation Conference. New York: ACM, 2001: 530-535.

[4] KOSHIMURA M, ZHANG T, FUJITA H, et al. QMaxSAT: a partial Max-SAT solver system description [J]. Journal on Satisfiability, Boolean Modeling and Computation, 2012, 8(1/2): 95-100.

[5] ZHANG L T, MADIGAN C F, MOSKEWICZ M H, et al. Efficient conflict driven learning in a boolean satisfiability solver [C]// ICCAD 2001: Proceedings of the 2001 IEEE/ACM International Conference on Computer-Aided Design. Piscataway, NJ: IEEE, 2001: 279-285.

[6] LIU Y L, LI C M, HE K, et al. Breaking cycle structure to improve lower bound for Max-SAT [C]// FAW 2016: Proceeding of the 11th International Workshop on Frontiers in Algorithmics, LNCS 9711. Berlin: Springer, 2016: 111-124.

[7] AUDEMARD G, SIMON L. Predicting learnt clauses quality in modern SAT solvers [C]// IJCAI 2009: Proceeding of the 2009 International Joint Conference on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 2009: 399-404.

[8] AUDEMARD G, LAGNIEZ J M, SIMON L. Improving glucose for incremental SAT solving with assumption: application to MUS extraction [C]// SAT 2013: Proceedings of the 16th International Conference on Theory and Applications of Satisfiability Testing. Berlin: Springer, 2013: 309-317.

[9] DE KLERK E. Aspects of Semidefinite Programming [M]. Berlin: Springer, 2002: 211-228.

[10] 劉燕麗,李初民,何琨.基于優化沖突集提高下界的MaxSAT完備算法[J].計算機學報,2013,36(10):2087-2095.(LIU Y L, LI C M, HE K. Improved lower bounds in MAXSAT complete algorithm based optimizing inconsistent set [J]. Chinese Journal of Computers, 2013, 36(10): 2087-2095.)

[11] 劉燕麗,黃飛,張婷.基于環型擴展推理規則的MaxSAT完備算法[J].南京大學學報(自然科學版),2015,51(4):762-771.(LIU Y L, HUANG F, ZHANG T. MaxSAT complete algorithm based cycle extended inference rules [J]. Journal of Nanjing University (Natural Sciences), 2015, 51(4): 762-771.)

[12] AUDEMARD G, SIMON L. Lazy clause exchange policy for parallel SAT solvers [C]// SAT 2014: Proceedings of the 2014 17th International Conference on Theory and Applications of Satisfiability Testing, LNCS 8561. Berlin: Springer, 2014: 197-205.

This work is partially supported by the Science and Technology Project of Hubei Provincial Education Department (B2016015).

LIUYanli, born in 1980, M. S., lecturer. Her research interests include algorithm design of NP problem, algorithm optimization.

XUZhenxing, born in 1990, Ph. D. candidate. His research interests include approximate solution of NP problem, algorithm optimization.

XIONGDan, born in 1979, M. S., lecturer. Her research interests include mathematical statistics, system identification.

ExactSATalgorithmbasedondynamicbranchingstrategyofawardandpunishment

LIU Yanli1,2*, XU Zhenxing2, XIONG Dan1

(1.CollegeofScience,WuhanUniversityofScienceandTechnology,WuhanHubei430081,China;2.SchoolofComputerScienceandTechnology,HuazhongUniversityofScienceandTechnology,WuhanHebei430074,China)

The limited number and high similarity of learning clauses lead to limited historical information and imbalanced search tree. In order to solve the problems, a dynamic branching strategy of award and punishment was proposed. Firstly, the variables of every unit propagation were punished. Different penalty functions were established according to whether the variable generated a conflict and the conflict interval. Then, in the learning phase, the positive variables for the conflict were found according to the learning clauses, and their activities were nonlinearly increased. Finally, the variable with the maximum activity was chosen as the new branching variable. On the basis of the glucose3.0 algorithm, an improved dynamic algorithm of award and punishment named Award and Punishment 7 (AP7) was completed. The experimental results show that, compared with the glucose3.0 algorithm, the rate of cutting branches of AP7 algorithm is improved by 14.2%-29.3%, and that of a few examples is improved up to 51%. The running time of the improved AP7 algorithm is shortened more than 7% compared with the glucose3.0 algorithm. The branching strategy can efficiently reduce the size of search tree, make the search tree more balanced and reduce the computation time.

Non-deterministic Polynomial Complete problem (NPC); SATisfiability problem (SAT); conflict driven clause learning; exact algorithm; branching strategy

2017- 06- 07;

2017- 08- 03。

湖北省教育廳科學研究計劃項目(B2016015)。

劉燕麗(1980—)，女，河南西平人，講師，碩士，CCF會員，主要研究方向： NP問題的算法設計、算法優化； 徐振興(1990—)，男，湖北鄂州人，博士研究生，主要研究方向：NP問題的近似求解、算法優化； 熊丹(1979—)，女，湖北天門人，講師，碩士，主要研究方向：數理統計、系統辨識。

1001- 9081(2017)12- 3487- 06

10.11772/j.issn.1001- 9081.2017.12.3487

(*通信作者電子郵箱yanlil2008@163.com)

TP301.6

A