基于特征加權理論的數據聚類算法*

費賢舉，李 虹，田國忠

(1.常州工學院 計算機信息工程學院，江蘇 常州 213032；2.吉林省質檢檢測基地 吉林省纖維檢驗處，長春 130103)

基于特征加權理論的數據聚類算法*

費賢舉1，李 虹2，田國忠1

(1.常州工學院 計算機信息工程學院，江蘇 常州 213032；2.吉林省質檢檢測基地 吉林省纖維檢驗處，長春 130103)

針對數據挖掘過程中數據聚類操作的初始聚類數目和初始聚類中心確定困難的問題，提出了一種軟子空間結合競爭合并機制的模糊加權聚類算法.通過對軟子空間聚類算法的目標函數進行改寫，并結合數據簇勢的大小對各數據簇進行競爭與合并操作，實現了對數據的聚類處理.結果表明，該算法能夠準確地對數據樣本進行聚類，并且聚類結果與初始數據簇數目和初始聚類中心無關，能夠滿足對高維數據聚類處理的需要，具有較好的實際應用價值.

數據挖掘；數據聚類；特征加權；軟子空間聚類；競爭合并機制；模糊聚類算法；聚類中心；聚類數目

信息時代中人們時刻都面臨著各種類型的數據，這些數據對生產生活具有重要影響.隨著技術的發展，數據信息成指數級快速增長.如何利用這些數據，如何在數據中發現所需信息成為當前的研究熱點.數據挖掘技術[1-6]作為海量數據處理的有效手段，越來越受到人們的重視.數據挖掘通過分析并處理特定類型的數據，發現其中包含的潛在規律，輔助人們做出正確的決策.數據挖掘分為數據準備、信息挖掘和結果解釋三個步驟.信息挖掘通過處理數據來發現其內部包含的規律信息或潛在價值，是數據挖掘的重點.信息挖掘的方法包括監督學習、關聯分析、聚類分析和特征選擇及提取[7-12]等.聚類分析是指利用特定技術手段發現數據的內在規律，并按照規律將數據進行科學分類.聚類分析是數據挖掘的重要方法和關鍵過程，直接影響數據挖掘的最終結果，是當前數據挖掘領域的重點研究內容之一.

軟子空間聚類算法是聚類分析算法的重要組成部分.軟子空間聚類算法通過給數據的不同特征賦予加權系數來區分特征之間的重要性，實現對聚類結果的靈活控制.影響軟子空間聚類算法效果的關鍵因素包括數據簇數目和初始聚類中心兩個方面.優秀的聚類算法要能夠收斂到合理的聚類數目并且聚類中心的初始選擇對聚類結果影響較小.目前流行的聚類方法包括數據簇評估準則法、聚類可視化法和模糊聚類法等.這些方法雖然能夠得到合理的聚類數目，但是對數據各方面特征的考慮還不全面.本文在軟子空間聚類算法的基礎上引入競爭合并機制，提出了一種軟子空間結合競爭合并機制的模糊加權聚類算法，結合了軟子空間算法和競爭合并機制的優點，實現了可靠聚類到合理數目和初始化聚類中心不影響聚類結果的目標.

1 算法模型

軟子空間聚類算法也稱為特征加權聚類算法，是指在數據的處理過程中為每個數據簇的特征賦予加權系數來標記特征的重要性.基于競爭合并機制的模糊聚類算法利用正則化項來使各個聚類中心競爭合并，最后得到滿足要求的聚類數目.將軟子空間聚類算法與競爭合并的模糊聚類算法相結合，可以得到軟子空間結合競爭合并機制的模糊加權聚類算法的目標函數，即

(1)

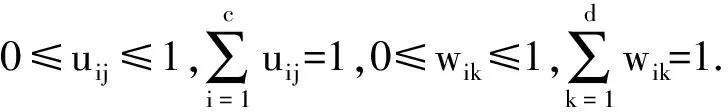
式(1)中前半部分用于計算各數據點到聚類中心的模糊加權距離和，后半部分計算各數據簇的勢平方和.當聚類中心數為n時，前半部分最小；當聚類中心數為1時，后半部分最小.合理選擇α并使J最小可得到滿足條件的數據簇數和聚類中心位置.利用拉格朗日乘子法原理并采用迭代求解的方法求滿足J最小時的vik.根據要求設置初始聚類中心數目c、聚類中心vik、模糊加權指數m和模糊隸屬度uij，迭代過程如下所示.

1) 計算聚類中心vik、特征加權系數wik和第i個數據簇的勢Ni，其計算公式分別為

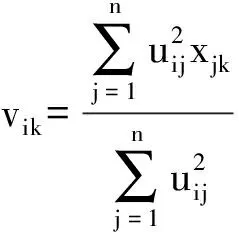
(2)

(3)

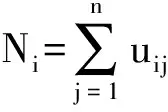
(4)

2) 計算正則項系數α.正則項系數用于調節目標函數中前后兩部分的比重，需要根據聚類中心和加權系數等參數動態計算，其計算公式為

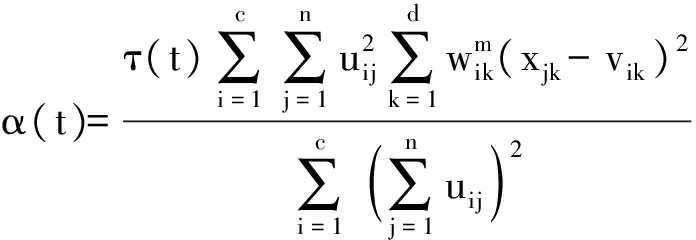
(5)

式中：t為迭代次數；τ(t)為每次迭代中的學習因子，其計算公式為

τ(t)=τ0exp(-|t-t0|/ζ)

(6)

其中：τ0為學習因子初始值；t0和ζ為根據實際情況選擇的常量.

3) 計算模糊隸屬度uij，其計算公式為

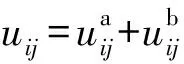
(7)

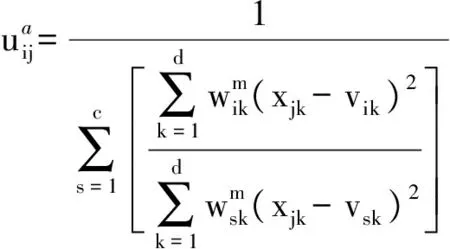
(8)

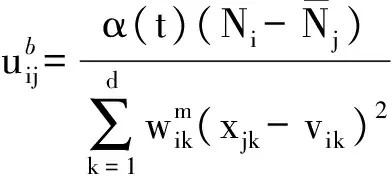
(9)

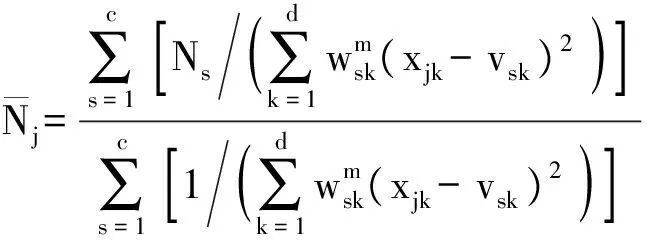
(10)

4) 計算數據簇勢的閾值MT和各個聚類中心之間的距離D，并求出距離D的最小值Dmin.當某個數據簇的勢Ni小于閾值MT時，就消去該數據簇.當Dmin滿足式(12)時，合并距離為Dmin的兩個數據簇.MT公式和判別條件分別為

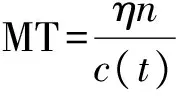
(11)

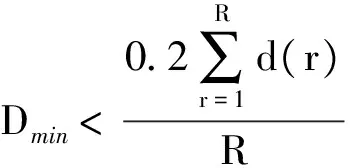
(12)

式中：η為合并閾值參數；c(t)為t次迭代時的聚類中心數；d(r)為兩個聚類中心之間的距離數值；R為各個聚類中心之間的距離數據總數，其表達式為

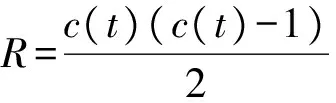
(13)

5) 根據削減和合并結果調整聚類中心數目c，當聚類中心數目保持穩定或滿足迭代結束條件時停止計算，所得的vik即為所需的聚類中心結果，否則返回步驟1)繼續執行.

2 試驗及結果分析

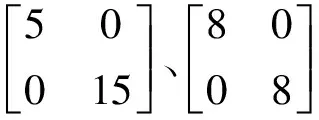
假設初始聚類中心數為15，學習因子初始值τ0為0.7，時間常量t0和ζ分別為10和15，合并閾值參數η為0.75，模糊加權指數m為3.數據點、真實聚類中心和初始聚類中心如圖1所示.

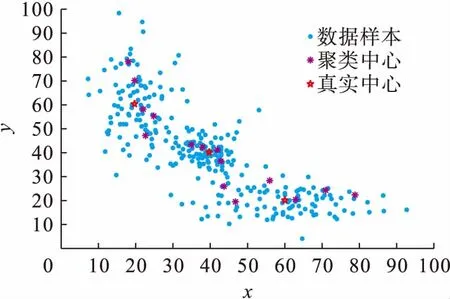
圖1 數據點及聚類中心分布Fig.1 Data points and distribution of clustering center

2.1 聚類準確性分析

迭代運算多次后，聚類結果如圖2所示.其中，圖2a表示2次迭代后，15個初始聚類中心還剩下10個；圖2b表示5次迭代后，聚類中心還剩下6個；圖2c表示9次迭代后，聚類中心還剩下5個；圖2d表示12次迭代后，聚類中心還剩下3個，在之后的迭代運算中聚類中心數目不再改變.由圖2可知，在迭代過程中，聚類中心的數目不斷減少，并且各個聚類中心的位置也在不斷變化.最后剩下的3個聚類中心的坐標已經非常接近各自的真實聚類中心，因此，該算法有比較好的聚類效果和聚類準確性.

圖2 聚類結果Fig.2 Clustering results

分別設置5組不同的真實聚類中心進行試驗.每組數據的產生方法與前述試驗相同，即指定相應的聚類中心，根據不同的協方差矩陣產生隨機的數據樣本.采用互信息指標作為評價聚類準確性的指標.互信息指標通過計算聚類結果與實際分類進行匹配后的平均互信息大小來標記正確分類的準確度，其計算公式為

(14)

式中：npq為真實類為p而被分為聚類結果q的數據個數；np為聚類結果為p的數據個數；nq為真實類為q的數據個數；N為總的數據個數.不同真實聚類中心NMI如表1所示.

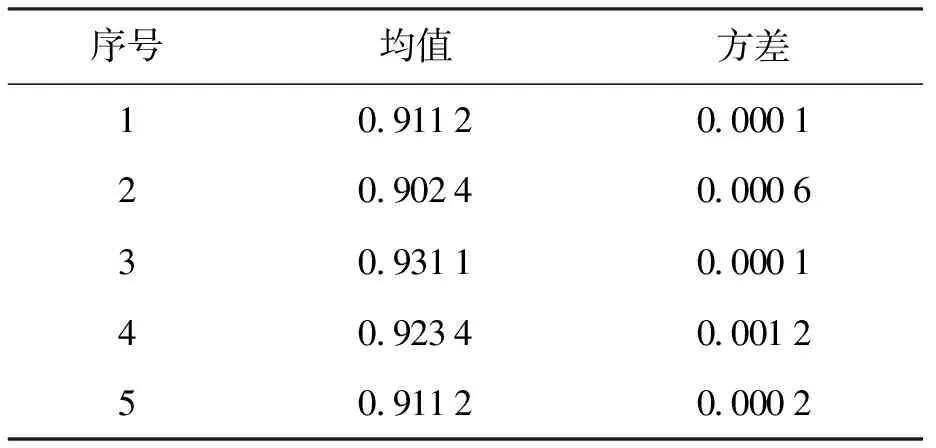
表1 聚類處理互信息指標數據表Tab.1 Mutual information index data table in cluster operation

由表1可知，聚類算法對數據聚類的準確度較高，且聚類結果不受真實聚類中心影響，因此，該算法能夠在各種情況下實現對數據樣本的可靠聚類.

2.2 初始聚類中心數目敏感性分析

分別選擇不同的初始聚類中心數進行運算，迭代過程中聚類中心數的變化情況如圖3所示.由圖3可知，雖然選擇的初始聚類中心數不同，迭代過程中聚類中心數目在不斷下降.經過若干次迭代后，聚類中心數目都穩定于3.因此，聚類算法對初始聚類中心數目變化不敏感，能夠可靠地收斂到合理的聚類中心數.

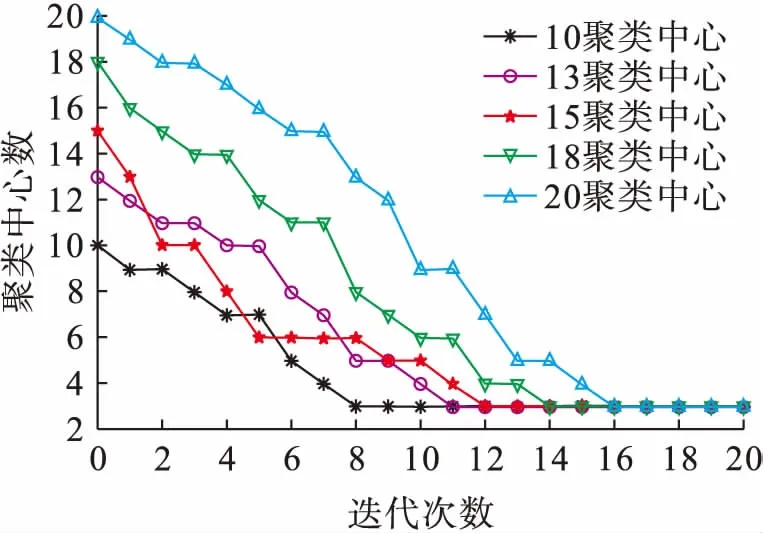
圖3 運算過程中聚類中心數Fig.3 Number of clustering center in operation process

2.3 初始聚類中心位置敏感性分析

隨機選擇15個初始聚類中心位置進行6次聚類處理，每次迭代過程中聚類中心數的減少情況如圖4所示.由圖4可知，在初始聚類中心不同時，經過若干次運算后聚類中心數目都穩定于3.因此，聚類算法對初始聚類中心位置的選擇不敏感，任意選擇初始聚類中心位置都能夠保證可靠地收斂于真實聚類中心.

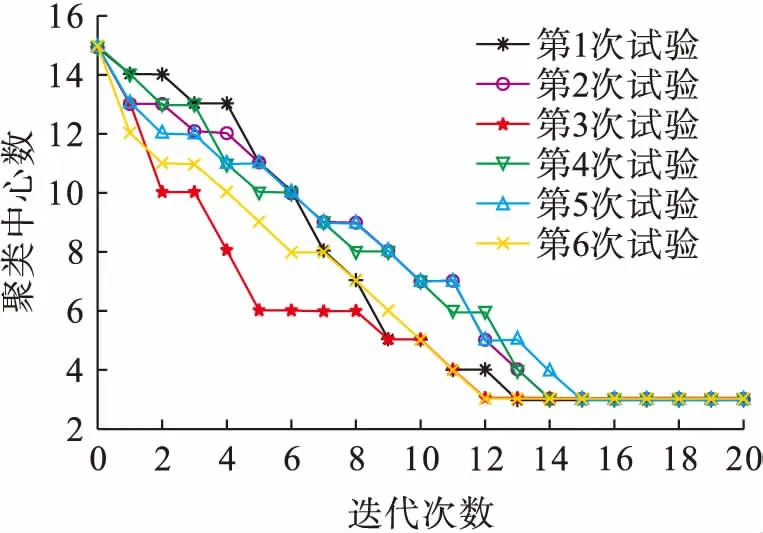
圖4 聚類處理過程中聚類中心數Fig.4 Number of clustering center in operation process

3 結 論

本文結合軟子空間聚類算法和基于競爭合并機制的模糊聚類算法，提出了一種軟子空間結合競爭合并機制的模糊加權聚類算法.該算法通過對軟子空間聚類算法的目標函數進行修改，使其具備了軟子空間聚類算法和競爭合并機制模糊聚類算法的優點.求解過程通過迭代的方式運行，能夠根據實際需要控制運算的速度和精度.結果表明，該算法能夠以較高的準確度實現對數據樣本的聚類分析，運算結果與初始數據簇的個數和初始聚類中心的位置無關，具有比較廣泛的適用性.

[1] 任艷.微信息大數據粗糙集的近似約簡 [J].沈陽工業大學學報，2016，38(3)：309-313.

(REN Yan.Approximate reduction of micro-message big data rough set [J].Journal of Shenyang University of Technology，2016，38(3)：309-313.)

[2] 劉城霞.基于MS關聯規則數據挖掘模型的應用與探討 [J].計算機技術與發展，2013，23(1)：25-28.

(LIU Cheng-xia.Application and discussion of data mining model based on microsoft association rules algorithm [J].Computer Technology and Development，2013，23(1)：25-28.)

[3] 張宇獻，劉通，董曉，等.基于改進劃分系統的模糊聚類有效性函數 [J].沈陽工業大學學報，2014，36(4)：431-435.

(ZHANG Yu-xian，LIU Tong，DONG Xiao，et al.Validity function for fuzzy clustering based on improved partition coeffcient [J].Journal of Shenyang University of Technology，2014，36(4)：431-435.)

[4] 陳晉音，何輝豪.基于密度的聚類中心自動確定的混合屬性數據聚類算法研究 [J].自動化學報，2015，41(10)：1798-1813.

(CHEN Jin-yin，HE Hui-hao.Research on density-based clustering algorithm for mixed data with determine cluster centers automatically [J].Acta Automa-tica Sinica，2015，41(10)：1798-1813.)

[5] 高志春，陳冠瑋，胡光波，等.傾斜因子K均值優化數據聚類及故障診斷研究 [J].計算機與數字工程，2014，42(1)：14-18.

(GAO Zhi-chun，CHEN Guan-wei，HU Guang-bo，et al.Fault diagnosis and optimal data clustering based on K-means with slope factor [J].Computer & Digital Engineering，2014，42(1)：14-18.)

[6] 劉云霞.基于動態時間規整的面板數據聚類方法研究及應用 [J].統計研究，2016，33(11)：93-101.

(LIU Yun-xia.Research and application of panel data clustering method based on dynamic time warping [J].Statistical Research，2016，33(11)：93-101.)

[7] 王德青，朱建平，王潔丹.基于自適應權重的函數型數據聚類方法研究 [J].數據統計與管理，2015，34(1)：84-92.

(WANG De-qing，ZHU Jian-ping，WANG Jie-dan.Research of clustering analysis for functional data based on adaptive weighting [J].Journal of Applied Statistic and Management，2015，34(1)：84-92.)

[8] 李因果，何曉群，李新春.基于Tucker3分解的三路數據聚類方法 [J].數理統計與管理，2016，35(1)：71-80.

(LI Yin-guo，HE Xiao-qun，LI Xin-chun.Three-way data clustering method based on tucker3 decomposition [J].Journal of Applied Statistic and Management，2016，35(1)：71-80.)

[9] 唐東明.基于Hadoop的仿射傳播大數據聚類分析方法 [J].計算機工程與應用，2015，51(4)：29-34.

(TANG Dong-ming.Affinity propagation clustering for big data based on Hadoop [J].Computer Engineering and Applications，2015，51(4)：29-34.)

[10]孫浩軍，閃光輝，高玉龍，等.一種高維混合屬性數據聚類算法 [J].計算機工程與應用，2015，51(8)：128-133.

(SUN Hao-jun，SHAN Guang-hui，GAO Yu-long，et al.Algorithm for clustering of high-dimensional data mixed with numeric and categorical attributes [J].Computer Engineering and Applications，2015，51(8)：128-133.)

[11]馬雯雯，鄧一貴.新的短文本特征權重計算方法 [J].計算機應用，2013，33(8)：2280-2282.

(MA Wen-wen，DENG Yi-gui.New feature weight calculation method for short text [J].Journal of Computer Applications，2013，33(8)：2280-2282.)

[12]胡先兵，趙國慶.引入時頻聚集交叉項干擾抑制的大數據聚類算法 [J].計算機科學，2016，43(4)：197-201.

(HU Xian-bing，ZHAO Guo-qing.Large data clustering algorithm introducing time and frequency clustering interference suppression [J].Computer Science，2016，43(4)：197-201.)

Dataclusteringalgorithmbasedonfeatureweightingtheory

FEI Xian-ju1, LI Hong2, TIAN Guo-zhong1

(1.School of Computer Information & Engineering, Changzhou Institute of Technology, Changzhou 213032, China; 2.Office of Fiber Inspection of Jilin Province, Quality Supervision and Inspection Base of Jilin Province, Changchun 130103, China)

Aiming at the problem that the initial clustering number and center are difficult to be determined in the data clustering opertion of data mining process, a fuzzy weighting clustering algorithm based on the soft subspace as well as the competition and combination mechanism was proposed.Through rewriting the objective function of soft subspace clustering algorithm and combining the size of data clusters, the competition and combination operation was carried out for the data clusters, and the clustering treatment of data was achieved.The results show that the proposed algorithm can accurately perform the clustering of data samples, and the clustering results are independent on the initial clustering number and center.The algorithm can meet the need in high dimensional data clustering processing and has the great practical value.

data mining; data clustering; feature weighting; soft subspace clustering; combination and competition mechanism; fuzzy clustering algorithm; clustering center; clustering number

2016-12-16.

國家自然科學基金資助項目(61363004).

費賢舉(1975-)，男，安徽合肥人，講師，碩士，主要從事數據挖掘、智能信息處理和數據可視化等方面的研究.

* 本文已于2017-12-22 15∶21在中國知網優先數字出版.網絡出版地址：http：//kns.cnki.net/kcms/detail/21.1189.T.20171222.0920.002.html

10.7688/j.issn.1000-1646.2018.01.14

TP 311

A

1000-1646(2018)01-0077-05

鐘 媛 英文審校：尹淑英)