基于遞歸小波神經網絡的UAV姿態變結構優化控制*
陳貴平
(貴州師范大學 大數據與計算機科學學院,貴陽 550001)
基于遞歸小波神經網絡的UAV姿態變結構優化控制*
陳貴平
(貴州師范大學 大數據與計算機科學學院,貴陽 550001)
無人機的姿態控制易受外界氣流干擾和模型參數攝動影響,為了提高其姿態控制的精度和穩定度,提出了將變結構控制與遞歸小波神經網絡相結合的優化魯棒控制律.構建并分析了無人機的姿態運動模型,采用變結構控制來設計無人機姿態運動的穩定控制律,將遞歸小波神經網絡加入到控制閉環回路中以實現變結構控制律的優化,減弱控制律對模型準確度的依賴性,并在仿真驗證中與傳統方法進行了比較.結果表明,該控制律能夠提高其姿態控制的穩定性,且具有較強魯棒性、較短收斂時間和較小能量消耗,從而證明了本文方法的有效性和可行性.
無人機;姿態控制;變結構控制;遞歸小波神經網絡;優化控制;穩定性;魯棒性;能量消耗
無人機的飛控系統是無人機系統的重要組成部分和關鍵核心技術,也是當前無人機控制應用領域的研究熱點.無人機要實現穩定的自主飛行,必須要實現對內外回路(姿態和位置)的有效控制,而內回路的穩定控制又是外回路控制的前提條件,即實現俯仰、偏航和滾動三個方向上的姿態控制.
目前,無人機的姿態控制是國內外學者的研究熱點[1-4].文獻[5]基于四元數來研究四軸無人機的姿態估計和控制,設計了梯度下降算法和比例微分控制器;文獻[6]將回溯法、滑模控制和神經網絡結合起來用于無人機的姿態控制,具有較好的魯棒性;文獻[7]設計了自結構動態遞歸模糊神經網絡來控制無人機的姿態運動,該方法比固定結構的模糊神經網絡具有更快的響應速度;文獻[8]針對難以建立無人機的精確數學模型這個問題,提出雙閉環復合控制策略分別對外環姿態和內環姿態角速度進行控制,并且在專業飛行軟件X-plane和仿真工具Matlab下進行了數學仿真;文獻[9]將無人機的姿態模型劃分為快慢兩個回路,分別利用最優廣義預測控制算法來設計控制律.
雖然上述方法具有較好的控制效果,但是沒有在實現姿態穩定控制的同時考慮控制性能的優化.為此,本文將變結構控制與遞歸小波神經網絡兩種方法相結合應用于無人機的姿態控制.根據變結構控制理論設計了穩定且魯棒的姿態控制律,將遞歸小波神經網絡嵌入到姿態控制回路中,利用其能夠逼近數學模型的優點,減弱了控制律對模型參數的依賴性,得到更加優化的控制效果.通過仿真實驗分析得到了無人機姿態角的變化曲線,并與傳統方法進行了比較,對比了優化前后的性能指標,證明了本文方法的有效性和可行性.
1 無人機姿態運動模型與分析
1.1 姿態運動模型
為了能夠準確描述無人機的姿態運動特征,以某型號無人機為分析研究對象,不考慮無人機的彈性和振動因素,建立其在飛行過程中的三通道姿態運動模型[10-11],即
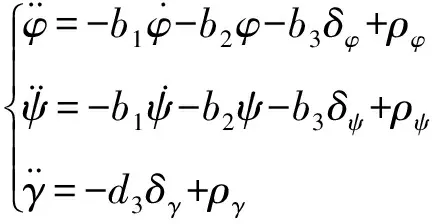
(1)
假定無人機在縱向運動上具有對稱性,可根據式(1)研究無人機俯仰角的跟蹤控制,將式(1)中的第一式改寫為

(2)
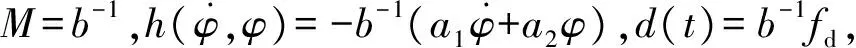
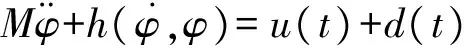
(3)
1.2 姿態運動分析
針對式(3)所示的無人機姿態運動模型,為了便于控制器設計,需要對其物理特性進行定常運動分析,給出兩個合理的假設.
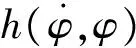
(4)
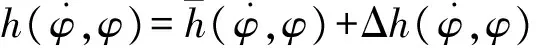
(5)
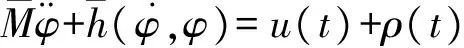
(6)
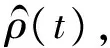
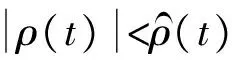
(7)
2 無人機姿態運動優化控制設計
2.1 變結構控制器設計
無人機姿態運動模型具有多變量、非線性的特性,因此,采用變結構控制器的設計方法可以使系統具有較強的魯棒性和更高的控制精度.
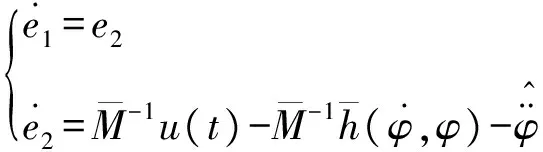
(8)
定義變結構控制中的滑模面為
s=ce1+e2
(9)
式中,c為固定常數.由式(8)可得滑模面的導數為
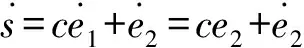
(10)
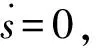
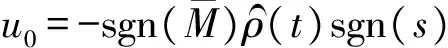
(11)
式中,sgn(s)=s/(|s|+λ),λ>0是一個較小的常數.因此,可以得到無人機姿態穩定的總控制律,即
u=u0+ueq=
(12)
2.2 基于遞歸小波神經網絡的控制律優化
由于無人機的姿態運動具有較強的非線性,且受參數變動和外部擾動影響,很容易引起控制系統的不穩定.為了減弱控制律對系統模型的依賴性,提高控制律的自適應性和魯棒性,使用遞歸小波神經網絡方法[12]來優化控制律.
2.2.1 遞歸小波神經網絡
遞歸小波神經網絡是遞歸神經網絡和小波神經網絡二者的結合,融合兩種神經網絡的優點,即結構簡單且動態性好,不僅能夠提高系統的穩定性,還可以動態地辨識非線性系統.
本文采用具有四層神經元的遞歸小波神經網絡,其分別為輸入層、小波層、產生層和輸出層.每一層的特征如下:
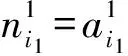
(13)
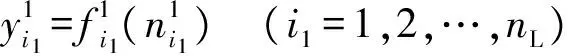
(14)
第二層為小波層,小波層的每個節點包括母波和反饋回路,母波的表達式為
δ(x)=-xe-x2/2
(15)
該層的輸入和輸出分別為
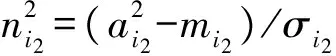
(16)
(17)
第三層為產生層,產生層的每個節點由乘積函數得到,其輸入和輸出分別為

(18)
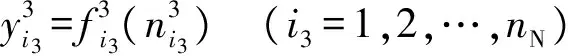
(19)
式中,nN為產生層的節點個數.
第四層為輸出層,輸出層的每個節點都是輸入信號之和,其輸入和輸出分別為
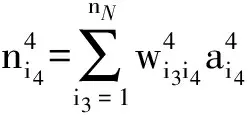
(20)
(21)
取m、σ和r分別為隱含層的參數,W為輸出權重矩陣,則整個遞歸小波神經網絡的輸出為
y(a,σ,m,r,W)=WTf(a,σ,m,r)
(22)
2.2.2 控制律優化
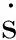
無人機姿態優化控制的系統框圖如圖1所示.將變結構控制的結果作為無人機姿態控制的期望值,并根據無人機的初始狀態及其姿態運動模型得到實際值,利用期望值與實際值的偏差來對無人機進行優化控制.
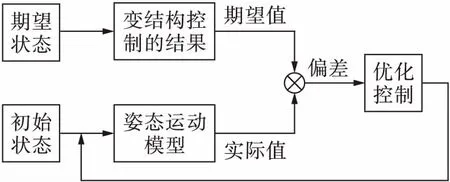
圖1 無人機姿態優化控制系統Fig.1 Optimized attitude control system for UAV
由梯度下降算法[13-14]來調整輸出層的權值,在外部擾動下,無人機俯仰角度的輸出、控制量的輸出和神經元的輸出分別為
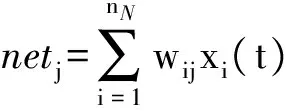
(23)
uj(k+1)=g(netj-θj,u(k))
(24)
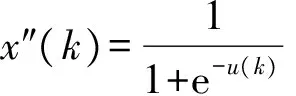
(25)
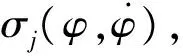
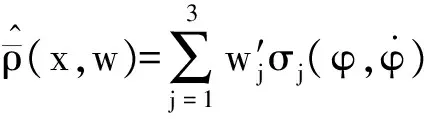
(26)
最終可根據圖1所示的方法實現無人機姿態的變結構優化控制.
3 仿真實驗與分析
為了體現本文方法的優勢,在進行仿真實驗與分析時,與傳統的PID控制方法進行了比較.定義無人機姿態控制的能量消耗為
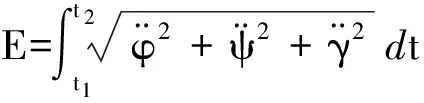
(27)
式中,t1和t2分別為控制的起始和結束時刻.仿真的初始條件如下:無人機的俯仰角、偏航角和滾動角的初始值分別為6°、8°和-10°,相對應的期望值分別為0°、0°和0°.仿真步長為0.05 s,對遞歸小波神經網絡的每一維進行五等分,其初始值的取值分別位于如下區間:[-10-3,10-3]、[-10-2,10-2]、[-2×10-3,2×10-3]、[-10-4,10-4]、[-10-3,10-3]、[-5×10-3,5×10-3].
根據上述仿真參數,分別采用本文方法和傳統PID方法進行實驗,得到的無人機俯仰角、偏航角和滾動角的仿真結果分別如圖2~4所示.可以看出,在本文方法的作用下,無人機的姿態角在較短時間內均能夠調節到期望值,且在控制過程中的時間變化曲線比較平滑,超調量較小,三個方向姿態角控制的收斂時間分別約為2.1、2.8和3.5 s.而傳統的PID控制在收斂時間上均比本文方法要長,分別為3.6、5.0和5.5 s.表1為本文方法和傳統PID方法在姿態控制過程中的能量消耗.從表1中可以看出,本文控制方法在能量消耗上要低于傳統的PID控制方法,優化率為32.84%.仿真實驗結果表明,本文控制方法在收斂時間和能量消耗上具有較明顯的優勢,證明了本文方法的有效性和可行性.
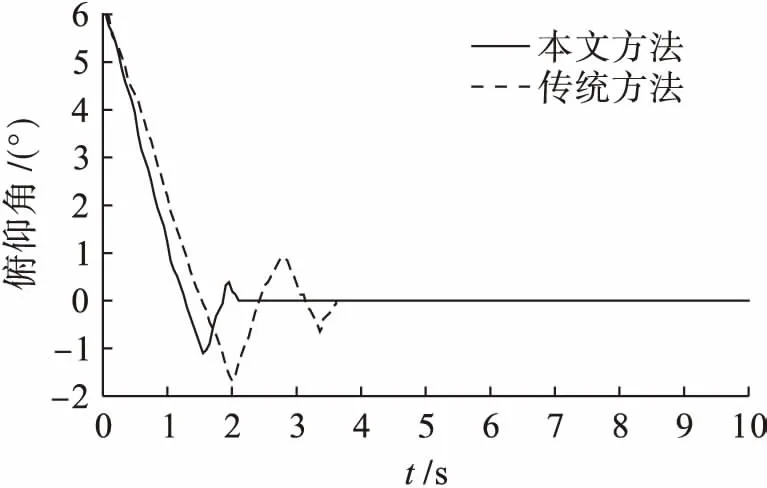
圖2 俯仰角控制結果的比較Fig.2 Comparison in control result of pitch angle
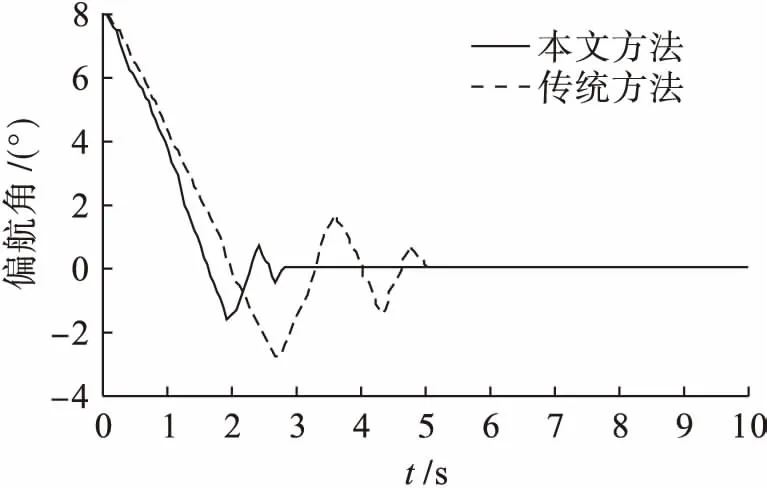
圖3 偏航角控制結果的比較Fig.3 Comparison in control result of yaw angle
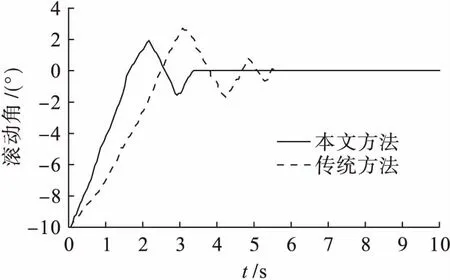
圖4 滾動角控制結果的比較Fig.4 Comparison in control result of roll angle

表1 能量消耗比較Tab.1 Comparison in energy consumption
4 結 論
本文將變結構控制與遞歸小波神經網絡相結合設計無人機的姿態控制律,不僅能夠解決模型不確定性和外界干擾的問題,減少控制律對模型的依賴程度,還可以使控制過程中的能量消耗更少,收斂時間更短.由仿真實驗得到的三個方向姿態角的時間變化曲線驗證了本文方法的有效性和可行性.本文方法不僅可以有效地提高無人機姿態控制的收斂速度和穩定度,而且能夠減少控制過程中的能量消耗,控制優化率能達到32.84%.
[1] 朱華勇,牛軼峰,沈林成,等.無人機系統自主控制技術研究現狀與發展趨勢 [J].國防科技大學學報,2010,32(3):115-120.
(ZHU Hua-yong,NIU Yi-feng,SHEN Lin-cheng,et al.State of the art and trends of autonomous control of UAV systems [J].Journal of National University of Defense Technology,2010,32(3):115-120.)
[2] 宗群,王丹丹,邵士凱,等.多無人機協同編隊飛行控制研究現狀及發展 [J].哈爾濱工業大學學報,2017,49(3):1-14.
(ZONG Qun,WANG Dan-dan,SHAO Shi-kai,et al.Research status and development of multi UAV coordinated formation flight control [J].Journal of Harbin Institute of Technology,2017,49(3):1-14.)
[3] Chang H,Duan H.Arificial bee colony optimized controller for unmanned rotorcraft pendulum [J].Aircraft Engineering and Aerospace Technology,2013,85(2):104-114.
[4] Cai G,Chen B M,Dong X,et al.Design and implementation of a robust and nonlinear flight control system for an unmanned helicopter [J].Mechatronics,2011,21(5):803-820.
[5] 冀亮,錢正洪,白茹.基于四元數的四軸無人機姿態的估計和控制 [J].現代電子技術,2015,38(11):112-116.
(JI Liang,QIAN Zheng-hong,BAI Ru.Attitude estimation and control of quaternion based quad-axis UAV [J].Modern Electronics Technique,2015,38(11):112-116.)
[6] 李明鎖.基于神經網絡的無人機滑模飛行控制設計 [J].測控技術,2012,32(1):96-100.
(LI Ming-suo.Sliding mode flight control for unmanned aerial vehicle based on neural networks [J].Measurement and Control Technology,2012,32(1):96-100.)
[7] 陳向堅,白越,續志軍,等.基于自結構動態遞歸模糊神經網絡的無人機姿態控制 [J].計算機應用研究,2011,28(9):3387-3389.
(CHEN Xiang-jian,BAI Yue,XU Zhi-jun,et al.Motion control for unmanned aircraft vehicle based on self-structuring recurrent fuzzy neural network [J].Application Research of Computers,2011,28(9):3387-3389.)
[8] 張興文,陳銘,曹飛,等.無人機姿態控制系統設計及仿真 [J].計算機仿真,2016,33(7):158-161.
(ZHANG Xing-wen,CHEN Ming,CAO Fei,et al.Design and simulation of UAV attitude control system [J].Computer Simulation,2016,33(7):158-161.)
[9] 張立珍,王慶宇,王迷迷,等.基于OGPC的無人機姿態控制律設計 [J].電光與控制,2017,24(4):19-22.
(ZHANG Li-zhen,WANG Qing-yu,WANG Mi-mi,et al.Design of UAV attitude control law based on the OGPC [J].Electronics Optics & Control,2017,24(4):19-22.)
[10]陳增強,李毅,孫明瑋,等.四旋翼無人機飛行器ADRC-GPC控制 [J].哈爾濱工業大學學報,2016,48(9):176-180.
(CHEN Zeng-qiang,LI Yi,SUN Ming-wei,et al.ADRC-GPC control of a quad-rotor unmanned aerial vehicle [J].Journal of Harbin Institute of Technology,2016,48(9):176-180.)
[11]王偉,胡鎮,馬浩,等.多旋翼傾轉定翼無人機的姿態控制 [J].計算機仿真,2014,31(1):31-35.
(WANG Wei,HU Zhen,MA Hao,et al.Attitude control for multi tile-wing UAV [J].Computer Simulation,2014,31(1):31-35.)
[12]劉斌,王潔,何廣軍,等.基于遞歸小波神經網絡的無人機反演控制 [J].計算機仿真,2016,33(2):116-121.
(LIU Bin,WANG Jie,HE Guang-jun,et al.Inversion control for unmanned aerial vehicle based on recurrent wavelet neural networks [J].Computer Simulation,2016,33(2):116-121.)
[13]丁惜瀛,王春強,李琳.基于對角遞歸神經網絡的汽車主動懸架控制 [J].沈陽工業大學學報,2015,37(1):6-10.
(DING Xi-ying,WANG Chun-qiang,LI Lin.Vehicle active suspension control based on diagonal recurrent neural network [J].Journal of Shenyang University of Technology,2015,37(1):6-10.)
[14]馬瑞,吳洪濤,丁力.基于人工蜂群算法的無人直升機LQG/LTR控制律優化設計 [J].控制與決策,2016,31(12):2248-2254.
(MA Rui,WU Hong-tao,DING Li.Optimal LQG/LTR controller for small-scale unmanned helicopter based on artificial bee colony algorithm [J].Control and Decision,2016,31(12):2248-2254.)
OptimizedcontrolforattitudevariablestructureofUAVbasedonrecurrentwaveletneuralnetworks
CHEN Gui-ping
(College of Big Data and Computer Science, Guizhou Normal University, Guiyang 550001, China)
The attitude control of unmanned aerial vehicle (UAV) is susceptible to the external air flow disturbance and model parameter perturbation.In order to improve the accuracy and stability of attitude control, an optimized robust control law was proposed based on variable structure control and recurrent wavelet neural networks.The attitude motion model for UAV was constructed and analyzed.A stabilized control law for the attitude motion of UAV was designed with the variable structure control.The recurrent wavelet neural networks were added into the control closed loop.Therefore, the variable structure control law could be optimized and the dependence of control law on the model accuracy could be weakened.In addition, the comparison with the traditional methods was performed in the simulation validation.The results show that the proposed control law can improve the stability of attitude control of UAV, and has strong robustness, shorter convergence time and less energy consumption, which proves the effectiveness and feasibility of the proposed method.
unmanned aerial vehicle; attitude control; variable structure control; recurrent wavelet neural network; optimized control; stability; robustness; energy consumption
2017-06-06.
貴州省科協專項及調研課題基金資助項目(201602).
陳貴平(1979-),男,貴州畢節人,副教授,碩士,主要從事大數據、信息安全和教育信息化等方面的研究.
* 本文已于2017-12-20 09∶59在中國知網優先數字出版.網絡出版地址:http://kns.cnki.net/kcms/detail/21.1189.T.20171220.0920.004.html
10.7688/j.issn.1000-1646.2018.01.17
TP 273
A
1000-1646(2018)01-0094-05
鐘 媛 英文審校:尹淑英)

