基于Kelly公式的倉(cāng)位管理策略及經(jīng)驗(yàn)證據(jù)

王志強(qiáng)，張 聰(東北財(cái)經(jīng)大學(xué) 金融學(xué)院，遼寧 大連 116025)

·金融與投資·

基于Kelly公式的倉(cāng)位管理策略及經(jīng)驗(yàn)證據(jù)

王志強(qiáng)，張 聰
(東北財(cái)經(jīng)大學(xué) 金融學(xué)院，遼寧 大連 116025)

基于Kelly公式及其擴(kuò)展模型，本文在倉(cāng)位管理理論分析的基礎(chǔ)上，用中國(guó)A股市場(chǎng)部分指數(shù)對(duì)最優(yōu)倉(cāng)位估計(jì)和倉(cāng)位管理策略進(jìn)行了經(jīng)驗(yàn)分析。研究結(jié)果表明：(1)中國(guó)A股市場(chǎng)中存在實(shí)現(xiàn)資產(chǎn)長(zhǎng)期增長(zhǎng)率最大化的最優(yōu)倉(cāng)位，進(jìn)行倉(cāng)位管理是有利可圖的。(2)倉(cāng)位管理的額外回報(bào)源于其高杠桿。(3)簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略無(wú)法達(dá)到最優(yōu)倉(cāng)位，會(huì)造成資產(chǎn)的重大損失。(4)經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略能夠顯著提高資產(chǎn)增長(zhǎng)率，但不能完全戰(zhàn)勝買入持有策略。(5)買賣信號(hào)增強(qiáng)的經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略能夠完勝買入持有策略，尤其是對(duì)偏重于大市值的指數(shù)效果更佳。

Kelly公式；倉(cāng)位管理；波動(dòng)率；交易杠桿；技術(shù)分析

一、問(wèn)題的提出

倉(cāng)位(Position)指投資者的風(fēng)險(xiǎn)資產(chǎn)市值占其總資產(chǎn)(風(fēng)險(xiǎn)資產(chǎn)+無(wú)風(fēng)險(xiǎn)資產(chǎn))市值的比率。倉(cāng)位與組合之間的區(qū)別在于，倉(cāng)位考察某類或某種風(fēng)險(xiǎn)資產(chǎn)占總資產(chǎn)的比率，而組合考察不同種類資產(chǎn)之間的比重。倉(cāng)位管理關(guān)注的是風(fēng)險(xiǎn)資產(chǎn)價(jià)格波動(dòng)給投資者帶來(lái)的損失，倉(cāng)位管理的目標(biāo)是使得投資者資產(chǎn)的長(zhǎng)期增長(zhǎng)率最大，是一個(gè)多期投資決策問(wèn)題，其核心在于應(yīng)對(duì)風(fēng)險(xiǎn)資產(chǎn)收益波動(dòng)的不對(duì)稱性；組合選擇關(guān)注的是不同種類資產(chǎn)之間的搭配給整個(gè)組合帶來(lái)的收益與風(fēng)險(xiǎn)變化，組合選擇的目標(biāo)是組合的效用最大化，是一個(gè)單期投資決策問(wèn)題，其核心在于應(yīng)對(duì)不同資產(chǎn)收益之間的相關(guān)性。

倉(cāng)位管理的一個(gè)理論基礎(chǔ)是Kelly公式，它是Kelly[1]通過(guò)研究博彩者在追求財(cái)富長(zhǎng)期增長(zhǎng)最大化的目標(biāo)下如何選擇投注而得到的。Kelly[1]的研究結(jié)果顯示，在一個(gè)可以進(jìn)行無(wú)限次投注的博彩游戲中，博彩者每次按其財(cái)富的某一比率(被稱之為最優(yōu)投注比率)進(jìn)行投注，可以使得自己的財(cái)富長(zhǎng)期增長(zhǎng)最大。當(dāng)然，該模型假設(shè)博彩者的財(cái)富是無(wú)限可分的，且所有財(cái)富(包括本金和利潤(rùn))都可以用于博彩游戲。將Kelly公式應(yīng)用到股票市場(chǎng)，計(jì)算出其最優(yōu)投注比率，就是我們需要的最優(yōu)倉(cāng)位[2]。考慮到股票價(jià)格的波動(dòng)特點(diǎn)，其中需要假設(shè)：(1)投資者的目標(biāo)是使資產(chǎn)長(zhǎng)期增長(zhǎng)率最大化。(2)每期投資僅在股票資產(chǎn)(可以是個(gè)股也可以是股票組合或指數(shù))和現(xiàn)金之間選擇。(3)股票價(jià)格變動(dòng)遵循幾何布朗運(yùn)動(dòng)，這意味著股票短期收益率近似服從正態(tài)分布，每期收益率獨(dú)立同分布。結(jié)果顯示，最優(yōu)倉(cāng)位與股票收益率的期望值正相關(guān)，與股票收益率的方差負(fù)相關(guān)。投資者應(yīng)根據(jù)對(duì)未來(lái)收益率及其波動(dòng)的預(yù)期來(lái)決定做多還是做空，是加倉(cāng)還是減倉(cāng)，是提高杠桿還是降低杠桿。簡(jiǎn)言之，由于股票收益波動(dòng)存在不對(duì)稱性，最優(yōu)倉(cāng)位能夠讓投資者在損失的情況下不至于傷筋動(dòng)骨，在盈利的情況下盡可能實(shí)現(xiàn)快速增值。

后續(xù)的相關(guān)研究主要圍繞上述三個(gè)假設(shè)或放松或擴(kuò)展進(jìn)行展開：(1)由于資產(chǎn)長(zhǎng)期增長(zhǎng)率的目標(biāo)函數(shù)中沒(méi)有考慮風(fēng)險(xiǎn)因素，因而許多研究者將該目標(biāo)函數(shù)擴(kuò)展到包含風(fēng)險(xiǎn)的各種效用函數(shù)。(2)部分研究將一項(xiàng)風(fēng)險(xiǎn)資產(chǎn)擴(kuò)展到多項(xiàng)風(fēng)險(xiǎn)資產(chǎn)，并考慮各項(xiàng)風(fēng)險(xiǎn)資產(chǎn)之間的相關(guān)性。(3)考慮風(fēng)險(xiǎn)資產(chǎn)的收益率并不獨(dú)立同分布于正態(tài)分布，而是具有尖峰厚尾和時(shí)間序列相關(guān)特性，因而部分研究主要采用經(jīng)驗(yàn)研究方法考察Kelly公式的實(shí)用效果。

在目標(biāo)函數(shù)方面，Samuelson[3]將最大化資產(chǎn)長(zhǎng)期增長(zhǎng)的目標(biāo)函數(shù)換成冪效用函數(shù)考察最優(yōu)倉(cāng)位，研究結(jié)果顯示，最優(yōu)倉(cāng)位獨(dú)立于投資者的財(cái)富水平，每期中投資者根據(jù)其總資產(chǎn)的某一比率投資于風(fēng)險(xiǎn)資產(chǎn)。Hakansson[4]采用四種效用函數(shù)(包括正冪效用函數(shù)、負(fù)冪效用函數(shù)、對(duì)數(shù)效用函數(shù)和指數(shù)效用函數(shù))將Samuelson[3]的研究問(wèn)題擴(kuò)展到更一般的形式，得到類似結(jié)果。Merton和Samuelson[5]將最大化資產(chǎn)長(zhǎng)期增長(zhǎng)的目標(biāo)函數(shù)簡(jiǎn)單直接地?cái)U(kuò)展為對(duì)數(shù)效用函數(shù)，結(jié)果發(fā)現(xiàn)將其用于多期投資決策時(shí)風(fēng)險(xiǎn)較高。Miller[6]的研究結(jié)果表明，當(dāng)投資期限趨近無(wú)窮大時(shí)，最大化資產(chǎn)的期望對(duì)數(shù)效用函數(shù)所得到的投資比重是最優(yōu)的，此時(shí)資產(chǎn)的長(zhǎng)期增長(zhǎng)率主要取決于資產(chǎn)的期望收益率。Aucamp[7]的研究結(jié)果顯示，在跨期和不確定環(huán)境中，采用最優(yōu)倉(cāng)位策略進(jìn)行投資的話，需要非常長(zhǎng)的投資期限才能實(shí)現(xiàn)資產(chǎn)長(zhǎng)期增長(zhǎng)最大化的目標(biāo)。但從中期來(lái)看，只要資產(chǎn)風(fēng)險(xiǎn)較小，最優(yōu)倉(cāng)位策略優(yōu)于其他策略。Maclean等[8]模擬了Kelly最優(yōu)倉(cāng)位策略中期運(yùn)行效果，其研究表明Kelly最優(yōu)倉(cāng)位策略不但可以實(shí)現(xiàn)資產(chǎn)長(zhǎng)期增長(zhǎng)的最大化，而且能夠避免破產(chǎn)的發(fā)生，另外還優(yōu)于所有其他策略。

擴(kuò)展到多項(xiàng)資產(chǎn)情形，Maslov和Zhang[9]假設(shè)組合中各資產(chǎn)價(jià)格變動(dòng)遵循多維幾何布朗運(yùn)動(dòng)，將單項(xiàng)資產(chǎn)形式擴(kuò)展到多項(xiàng)資產(chǎn)形式，得到與單項(xiàng)資產(chǎn)形式類似的結(jié)果。Medo等[10]考察了相互獨(dú)立的多項(xiàng)資產(chǎn)情形，結(jié)果顯示，在不超過(guò)5項(xiàng)資產(chǎn)的情形下，能夠得出最優(yōu)倉(cāng)位的解析解；超過(guò)5項(xiàng)資產(chǎn)，只能采用數(shù)值方法近似求解。Medo和Zhang[11]考察了存在相關(guān)性的多項(xiàng)資產(chǎn)情形，結(jié)果發(fā)現(xiàn)，組合中風(fēng)險(xiǎn)資產(chǎn)之間的正相關(guān)會(huì)導(dǎo)致組合中資產(chǎn)的配置比重相應(yīng)減少。

在經(jīng)驗(yàn)分析方面，Samuelson[12]的研究結(jié)果顯示，從長(zhǎng)期來(lái)看，采用最優(yōu)倉(cāng)位策略的基金經(jīng)理將獲得更多的資產(chǎn)增長(zhǎng)；即使風(fēng)險(xiǎn)資產(chǎn)的期望收益為正，Kelly最優(yōu)倉(cāng)位策略在長(zhǎng)期投資期限內(nèi)也可能出現(xiàn)虧損，在實(shí)際運(yùn)用時(shí)要做好風(fēng)險(xiǎn)控制；相對(duì)于基于其他效用函數(shù)的倉(cāng)位管理策略，Kelly最優(yōu)倉(cāng)位策略最優(yōu)。Rotando和Thorp[13]基于S&P500指數(shù)考察了Kelly最優(yōu)倉(cāng)位策略的實(shí)用效果，發(fā)現(xiàn)其具有相對(duì)比較優(yōu)勢(shì)。Maclean等[14]基于資產(chǎn)增長(zhǎng)與安全的測(cè)度方法考察了動(dòng)態(tài)投資過(guò)程中資產(chǎn)增長(zhǎng)與安全問(wèn)題，研究表明，風(fēng)險(xiǎn)資產(chǎn)的配置比重不能超過(guò)Kelly最優(yōu)倉(cāng)位。如果風(fēng)險(xiǎn)資產(chǎn)的配置比重超過(guò)Kelly最優(yōu)倉(cāng)位，投資風(fēng)險(xiǎn)增加，資產(chǎn)增長(zhǎng)率降低，他們認(rèn)為Kelly最優(yōu)倉(cāng)位策略優(yōu)于其他策略。Anderson和Faff[15]用五分鐘高頻期貨數(shù)據(jù)對(duì)Kelly最優(yōu)倉(cāng)位策略進(jìn)行回測(cè)和檢驗(yàn)，結(jié)果表明，倉(cāng)位管理策略在期貨交易中非常重要，只有清楚倉(cāng)位管理的可行范圍，才能避免破產(chǎn)，同時(shí)實(shí)現(xiàn)資產(chǎn)長(zhǎng)期增長(zhǎng)率的最大化。

國(guó)內(nèi)對(duì)基于Kelly公式的倉(cāng)位管理研究相對(duì)較少。凌士勤[16]提出了基于VAR及Kelly增長(zhǎng)體系的“基于最優(yōu)增長(zhǎng)路徑的增長(zhǎng)-安全模型”，并在離散條件下，用基于情景分析的方法考察了模型的實(shí)用效果，他認(rèn)為該模型可作為投資活動(dòng)的一種實(shí)踐工具。羅勇[17]基于Kelly理論，建立了風(fēng)險(xiǎn)約束下的Kelly動(dòng)態(tài)投資組合模型，采用理論模型和經(jīng)驗(yàn)分析研究了在最大資金衰落與交易成本約束下的基金資產(chǎn)動(dòng)態(tài)最優(yōu)增長(zhǎng)問(wèn)題。

綜上所述，筆者認(rèn)為，已有的相關(guān)研究存在兩個(gè)不足：第一，理論模型的假設(shè)與現(xiàn)實(shí)不完全相同致使Kelly最優(yōu)倉(cāng)位管理策略的效果無(wú)法保證。事實(shí)上，許多證據(jù)顯示風(fēng)險(xiǎn)資產(chǎn)收益率并不獨(dú)立同分布于正態(tài)分布，而是具有尖峰厚尾和時(shí)間序列相關(guān)特性，這要求Kelly最優(yōu)倉(cāng)位管理策略的實(shí)效性需要回測(cè)與檢驗(yàn)。第二，已有的國(guó)內(nèi)外相關(guān)研究并沒(méi)有告訴我們Kelly最優(yōu)倉(cāng)位管理策略在中國(guó)A股市場(chǎng)中是否適用。鑒于此，本文嘗試采用中國(guó)A股部分指數(shù)對(duì)Kelly最優(yōu)倉(cāng)位管理策略進(jìn)行回測(cè)和檢驗(yàn)，在此基礎(chǔ)上尋求更好的倉(cāng)位管理策略。

本文的可能貢獻(xiàn)在于：第一，首次嘗試采用中國(guó)A股市場(chǎng)指數(shù)回測(cè)與檢驗(yàn)最優(yōu)倉(cāng)位的存在性，我們確定最優(yōu)倉(cāng)位存在于中國(guó)A股市場(chǎng)，且其額外回報(bào)來(lái)源于投資者對(duì)交易杠桿的使用。第二，首次提出采用波動(dòng)率調(diào)整和買賣信號(hào)增強(qiáng)的方法動(dòng)態(tài)調(diào)整倉(cāng)位，經(jīng)驗(yàn)檢驗(yàn)結(jié)果證明該方法可以極大地提高投資者的收益率。

二、基于Kelly公式的倉(cāng)位管理理論分析

(一)基本模型：Kelly公式

假設(shè)一個(gè)博彩者的初始財(cái)富為W0，該博彩者可以將其財(cái)富的一部分不斷重復(fù)地投入到一個(gè)風(fēng)險(xiǎn)游戲中。每輪游戲中，博彩者贏的概率為p，輸?shù)母怕蕿?-p，如果獲勝，博彩者可以得到投注的兩倍，否則失去投注。若每輪游戲中博彩者的收益率為Rt，則博彩者贏時(shí)Rt=1，博彩者輸時(shí)Rt=-1。若博彩者每次下注比率(或投入比率，我們稱之為倉(cāng)位)為f，那么T期期末投資者的財(cái)富WT為：

(1)

由于每輪游戲中博彩者的收益率Rt可以視為獨(dú)立同分布于兩點(diǎn)分布(1,-1; p,1-p)，因而博彩者的資產(chǎn)長(zhǎng)期指數(shù)增長(zhǎng)率為[1]：

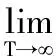
(2)

最大化式(2)獲得最優(yōu)倉(cāng)位為：

f*=(2p-1)×100%

(3)

式(3)顯示，如果贏的概率大于1/2，博彩者就下注，其最優(yōu)下注比率隨著概率增加而增加。譬如，贏的概率p=0.6000時(shí)最優(yōu)下注比率為20%，此時(shí)博彩者的資產(chǎn)長(zhǎng)期指數(shù)增長(zhǎng)率為2.03%。

(二)擴(kuò)展模型：Kelly公式的擴(kuò)展

將Kelly公式應(yīng)用到股票市場(chǎng)，同時(shí)考慮到股票市場(chǎng)的特點(diǎn)，我們假設(shè)投資者每期的收益率獨(dú)立同分布于兩點(diǎn)分布(rw, -rl; p, 1-p)，則投資者的資產(chǎn)長(zhǎng)期指數(shù)增長(zhǎng)率為：

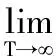
(4)

最大化式(4)可以得到最優(yōu)倉(cāng)位為：

f*=[prw-(1-p)rl]/rwrl×100%=E(R)/rwrl×100%

(5)

式(5)顯示，如果期望收益為正，投資者應(yīng)該做多；如果期望收益為負(fù)，投資者應(yīng)該做空。投資者的最優(yōu)倉(cāng)位大小與期望收益正相關(guān)，與rwrl負(fù)相關(guān)。實(shí)際上，由于該兩點(diǎn)分布的方差為Var(R)=p(1-p)(rw+rl)2，可以證明，當(dāng)p和E(R)固定不變的情況下，rwrl會(huì)隨著方差Var(R)增加而增大。因此，我們可以推出，該兩點(diǎn)分布的方差越大，最優(yōu)倉(cāng)位f*越小。這意味著，投資者的最優(yōu)倉(cāng)位大小與兩點(diǎn)分布的方差負(fù)相關(guān)。

考慮到股票收益率服從兩點(diǎn)分布的假設(shè)較為特殊，我們將假設(shè)改為常用的假設(shè)：股票價(jià)格S的變動(dòng)遵循幾何布朗運(yùn)動(dòng)，即dS=Sdt+Sdz，在此假設(shè)下股票價(jià)格服從對(duì)數(shù)正態(tài)分布，股票的短期收益率近似服從正態(tài)分布N(-2/2,)。考慮一個(gè)由股票和無(wú)風(fēng)險(xiǎn)資產(chǎn)組成的組合，其倉(cāng)位(或投資比率)分別為f和1-f，無(wú)風(fēng)險(xiǎn)收益率記為r，則投資者的資產(chǎn)長(zhǎng)期指數(shù)增長(zhǎng)率為：

g=fμ-1/2(fσ)2+(1-f)r

(6)

最大化式(6)可以得到最優(yōu)倉(cāng)位為：

f*=(μ-r)/σ2×100%

(7)

基于式(7)，我們從理論上進(jìn)一步證明了最優(yōu)倉(cāng)位與股票收益率的期望值正相關(guān)，與股票收益率的方差負(fù)相關(guān)。這表明，在收益率的方差不變的條件下，預(yù)期收益越高，最優(yōu)倉(cāng)位越大，投資者的資產(chǎn)長(zhǎng)期增長(zhǎng)速度就越快；在期望收益率不變的條件下，收益率的方差越大，最優(yōu)倉(cāng)位越小，投資者的資產(chǎn)長(zhǎng)期增長(zhǎng)速度就越快。投資者應(yīng)根據(jù)對(duì)未來(lái)收益率及其波動(dòng)的預(yù)期，來(lái)決定做多還是做空，是加倉(cāng)還是減倉(cāng)，是提高杠桿還是降低杠桿。

需要說(shuō)明的是，最優(yōu)倉(cāng)位的計(jì)算公式建立在不同時(shí)期的投資收益是獨(dú)立同分布的，且每期的倉(cāng)位是固定的。實(shí)踐中，很多經(jīng)驗(yàn)證據(jù)顯示股票收益具有均值回復(fù)特點(diǎn)，且股價(jià)波動(dòng)具有聚集效應(yīng)，即股價(jià)波動(dòng)在一段時(shí)期內(nèi)較小而下一段時(shí)期較大，周而復(fù)始。

三、最優(yōu)倉(cāng)位估計(jì)：來(lái)自中國(guó)A股部分指數(shù)的經(jīng)驗(yàn)證據(jù)

(一)最優(yōu)倉(cāng)位測(cè)算

在下文的具體分析過(guò)程中，我們選擇中國(guó)A股市場(chǎng)中7個(gè)主要指數(shù)對(duì)最優(yōu)倉(cāng)位進(jìn)行回測(cè)和檢驗(yàn)，這7個(gè)指數(shù)分別是滬深300指數(shù)、上證指數(shù)、上證50指數(shù)、上證180指數(shù)、深圳成份指數(shù)、中小板指數(shù)和創(chuàng)業(yè)板指數(shù)。之所以選擇指數(shù)進(jìn)行回測(cè)和檢驗(yàn)，是因?yàn)橹笖?shù)收益率相對(duì)于個(gè)股收益率更接近正態(tài)分布，這一結(jié)果獲得許多經(jīng)驗(yàn)證據(jù)支持，同時(shí)也是因?yàn)椴糠种笖?shù)可以通過(guò)相關(guān)的衍生產(chǎn)品進(jìn)行杠桿交易或做空交易。我們使用這7個(gè)指數(shù)周收益率的全部樣本分別估計(jì)其樣本均值和樣本方差，根據(jù)式(7)計(jì)算其最優(yōu)倉(cāng)位，這里我們不考慮閑置資金的無(wú)風(fēng)險(xiǎn)投資收益，即假設(shè)r=0，則f*=μ/σ2×100%。考慮到現(xiàn)行的漲跌停限制始于1996年年底，此前的股市波動(dòng)幅度顯著高于此后的股市，譬如，1995年5月15日至1995年5月19日上證指數(shù)上漲超過(guò)46%，1996年12月2日至1996年12月6日上證指數(shù)上漲超過(guò)17%，1996年12月16日至1996年12月20日上證指數(shù)下跌超過(guò)20%，我們對(duì)較早開始的上證指數(shù)和深圳成份指數(shù)增加了1997年之后的樣本區(qū)間進(jìn)行回測(cè)和檢驗(yàn)。具體測(cè)算結(jié)果如表1所示。

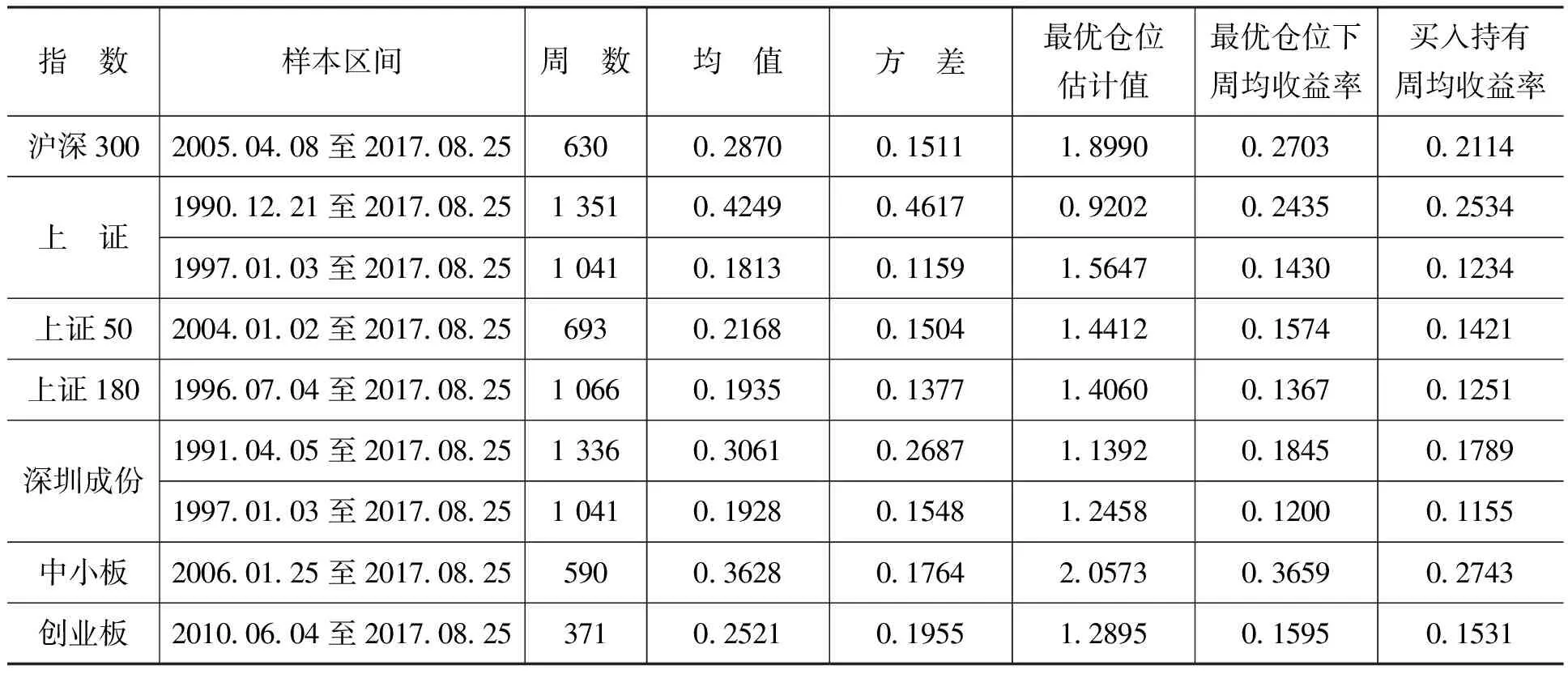
表1 基于指數(shù)的最優(yōu)倉(cāng)位估計(jì)與收益率測(cè)算 單位：周，%

注：周均收益率是指樣本區(qū)間內(nèi)總收益率的幾何平均收益率。下同。

從表1可以看出，第一，除了上證指數(shù)在1990年12月21日至2017年8月25日樣本區(qū)間內(nèi)的最優(yōu)倉(cāng)位估計(jì)值下周均收益率(0.2435%)低于該區(qū)間內(nèi)買入持有的周均收益率(0.2534%)之外，其他指數(shù)的最優(yōu)倉(cāng)位估計(jì)值下周均收益率均高于該區(qū)間內(nèi)買入持有的周均收益率。這表明，有一個(gè)更好的倉(cāng)位能夠讓投資指數(shù)的長(zhǎng)期收益超過(guò)簡(jiǎn)單被動(dòng)的買入持有收益。第二，除了上證指數(shù)在1990年12月21日至2017年8月25日樣本區(qū)間內(nèi)的最優(yōu)倉(cāng)位估計(jì)值(0.9202)小于1之外，其他指數(shù)的最優(yōu)倉(cāng)位估計(jì)值都大于1，這表明為實(shí)現(xiàn)高于買入持有策略的資產(chǎn)增長(zhǎng)率，投資者應(yīng)該借助杠桿手段加大倉(cāng)位。第三，滬深300指數(shù)和中小板指數(shù)的最優(yōu)倉(cāng)位估計(jì)值下周均收益率顯著高于該區(qū)間內(nèi)買入持有的周均收益率，其他指數(shù)不明顯。這表明，采用式(7)計(jì)算出的最優(yōu)倉(cāng)位估計(jì)值在實(shí)際應(yīng)用時(shí)應(yīng)該慎重。需要說(shuō)明的是，上述經(jīng)驗(yàn)結(jié)果并沒(méi)有考慮交易成本因素的影響，部分結(jié)果在實(shí)踐中的效果有待進(jìn)一步考察。

(二)不同倉(cāng)位下收益率測(cè)算與比較

表1的結(jié)果只能告訴我們，根據(jù)式(7)計(jì)算出的最優(yōu)倉(cāng)位估計(jì)值能夠讓投資指數(shù)的長(zhǎng)期收益超過(guò)簡(jiǎn)單被動(dòng)的買入持有收益，但是并不能說(shuō)明該估計(jì)值就是最優(yōu)倉(cāng)位，因?yàn)槲覀儾](méi)有證明該最優(yōu)倉(cāng)位估計(jì)值下周均收益率高于其他倉(cāng)位下的周均收益率。下面，我們以滬深300指數(shù)為例，考察最優(yōu)倉(cāng)位估計(jì)值下周均收益率是否高于其他倉(cāng)位下的周均收益率，如果該估計(jì)值下周均收益率均高于其他倉(cāng)位下的周均收益率，則證明該估計(jì)值是最優(yōu)倉(cāng)位，否則不是。為此，我們圍繞滬深300指數(shù)的最優(yōu)倉(cāng)位估計(jì)值(1.8990)，以0.1000為間隔向前向后各選擇9個(gè)倉(cāng)位計(jì)算其樣本區(qū)間內(nèi)總收益率和周均收益率，如表2所示。

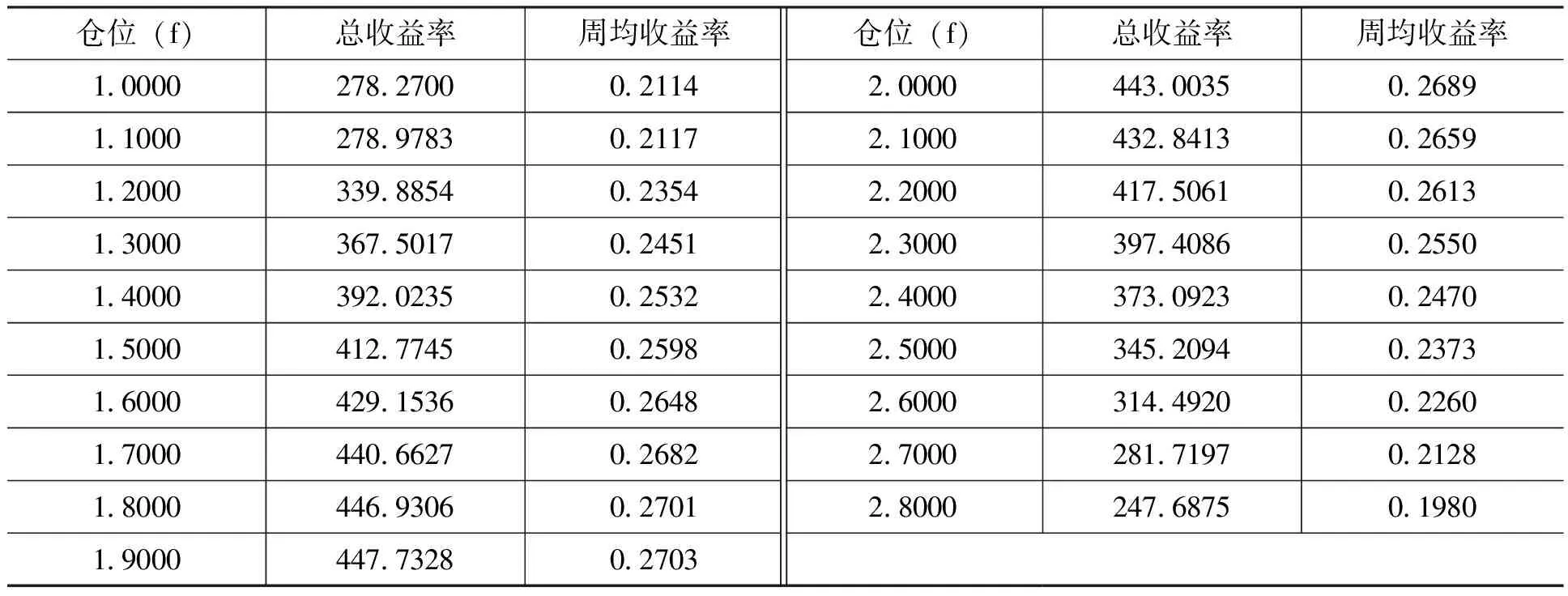
表2 不同倉(cāng)位下的收益率測(cè)算：基于滬深300指數(shù)周收益 單位：%

從表2可以看出，倉(cāng)位在1.9000下總收益率(447.7328%)和周均收益率(0.2703%)最高，樣本區(qū)間內(nèi)其他倉(cāng)位下總收益率和周均收益率均相對(duì)較小。這表明，1.9000的倉(cāng)位具有相對(duì)較強(qiáng)的長(zhǎng)期收益優(yōu)勢(shì)。

為了反映全貌，我們將小于1.0000的倉(cāng)位下總收益率和周均收益率也進(jìn)行了計(jì)算，如圖1和圖2所示。很明顯，在我們所考察的樣本區(qū)間內(nèi)最優(yōu)倉(cāng)位是1.9000。因此，結(jié)合從表1中得出的結(jié)果，我們認(rèn)為，中國(guó)A股市場(chǎng)中存在資產(chǎn)長(zhǎng)期增長(zhǎng)目標(biāo)下的最優(yōu)倉(cāng)位，倉(cāng)位管理是一件應(yīng)該考慮和值得去做的事情，投資者應(yīng)該借助杠桿手段加大倉(cāng)位，以實(shí)現(xiàn)資產(chǎn)的長(zhǎng)期高增長(zhǎng)。

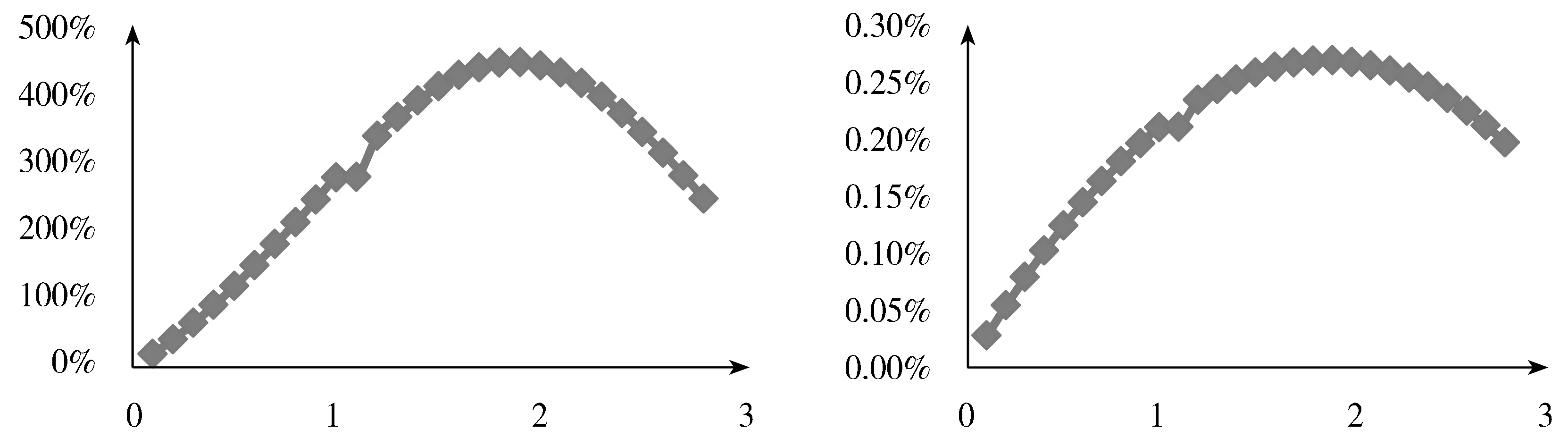
圖1 總收益率隨倉(cāng)位大小的變化 圖2 幾何平均收益率隨倉(cāng)位大小的變化

四、動(dòng)態(tài)倉(cāng)位管理策略的經(jīng)驗(yàn)證據(jù)

上文對(duì)最優(yōu)倉(cāng)位的估計(jì)與檢驗(yàn)中，采用的是固定倉(cāng)位方法，即整個(gè)樣本區(qū)間內(nèi)倉(cāng)位是固定的，但是這可能會(huì)引起前視偏差(Look-Ahead Bias)，在實(shí)踐中是行不通的。因此，實(shí)際操作中我們必須根據(jù)可獲取的相關(guān)數(shù)據(jù)，判斷是否采取動(dòng)態(tài)調(diào)整倉(cāng)位的管理策略進(jìn)行倉(cāng)位管理。本部分我們檢測(cè)簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略、經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略、考慮買賣信號(hào)的簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略和考慮買賣信號(hào)的經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略。

(一)簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略

一種最簡(jiǎn)單的動(dòng)態(tài)倉(cāng)位管理策略是基于當(dāng)期已有數(shù)據(jù)估計(jì)收益率的期望和方差，根據(jù)式(7)計(jì)算最優(yōu)倉(cāng)位，依據(jù)該最優(yōu)倉(cāng)位建倉(cāng)，下一期加入最新數(shù)據(jù)滾動(dòng)計(jì)算新的最優(yōu)倉(cāng)位，再依據(jù)新的最優(yōu)倉(cāng)位進(jìn)行調(diào)倉(cāng)，以此類推。我們采用過(guò)去50周(約一年)的周收益率估計(jì)當(dāng)期期望和當(dāng)期方差，根據(jù)式(7)計(jì)算最優(yōu)倉(cāng)位，然后計(jì)算當(dāng)期收益率，滾動(dòng)計(jì)算直至樣本期結(jié)束，最后計(jì)算整個(gè)樣本區(qū)間內(nèi)總收益率和幾何平均周收益率。具體測(cè)算結(jié)果列于表3的左邊。從表3可以看出，簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略的總收益率基本上等于或接近-100%，這意味著簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略在實(shí)踐中是行不通的，其原因在于短期內(nèi)股價(jià)的大幅波動(dòng)會(huì)導(dǎo)致當(dāng)期期望和當(dāng)期方差的估計(jì)值偏離理論值，進(jìn)而引起計(jì)算出的最優(yōu)倉(cāng)位遠(yuǎn)離真正的最優(yōu)倉(cāng)位。這種情況下，依據(jù)錯(cuò)誤的最優(yōu)倉(cāng)位進(jìn)行建倉(cāng)或調(diào)倉(cāng)就會(huì)很容易被短期內(nèi)股價(jià)的暴漲暴跌擊穿倉(cāng)位或者損失殆盡難以恢復(fù)。

(二)經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略

借鑒Barroso和Santa-Clara[18]對(duì)動(dòng)量崩潰(Momentum Crashes)的管理思想，我們的波動(dòng)率調(diào)整思路是，由于波動(dòng)率具有較好的預(yù)測(cè)性，可以采用自回歸模型預(yù)測(cè)其未來(lái)的波動(dòng)率，因而我們可以用波動(dòng)率的預(yù)測(cè)值修正或者調(diào)整最優(yōu)倉(cāng)位，具體而言，當(dāng)波動(dòng)率的預(yù)測(cè)值較高時(shí)調(diào)低倉(cāng)位，當(dāng)波動(dòng)率的預(yù)測(cè)值較低時(shí)調(diào)高倉(cāng)位。經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位用如下公式進(jìn)行計(jì)算：

fm=1+(Dmax-D)/(Dmax-Dmin)

(8)

其中，D、Dmax和Dmin分別表示當(dāng)期方差、過(guò)去n期內(nèi)最大方差和過(guò)去n期內(nèi)最小方差的估計(jì)值。

式(8)的含義是，當(dāng)期方差估計(jì)值相對(duì)較大的時(shí)候倉(cāng)位增加相對(duì)較小，當(dāng)期方差估計(jì)值相對(duì)較小的時(shí)候倉(cāng)位增加相對(duì)較大。這很容易理解，當(dāng)期方差估計(jì)值相對(duì)較大意味著市場(chǎng)波動(dòng)加大，風(fēng)險(xiǎn)增加，此時(shí)應(yīng)該輕倉(cāng)；當(dāng)期方差估計(jì)值相對(duì)較小意味著市場(chǎng)波動(dòng)減小，風(fēng)險(xiǎn)降低，此時(shí)應(yīng)該重倉(cāng)。理論上講，我們應(yīng)該在最優(yōu)倉(cāng)位的基礎(chǔ)上根據(jù)波動(dòng)率變化及其預(yù)測(cè)的高低進(jìn)行減倉(cāng)或加倉(cāng)的調(diào)整，但是考慮到我們要以滿倉(cāng)買入持有為比較基準(zhǔn)，分析經(jīng)波動(dòng)率調(diào)整的倉(cāng)位管理策略的幅度和效果，因而在式(8)中我們用滿倉(cāng)(即“1”)取代了最優(yōu)倉(cāng)位，同時(shí)也對(duì)減倉(cāng)或加倉(cāng)的調(diào)整項(xiàng)，即式(8)中等號(hào)右邊第二項(xiàng)做出了調(diào)整。

本文中，我們?nèi)為100周(約兩年)，根據(jù)式(8)計(jì)算經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位，每周滾動(dòng)調(diào)整倉(cāng)位。具體測(cè)算結(jié)果列于表3的中間。從表3可以看出，第一，除了上證180指數(shù)的收益率為負(fù)，總收益率和周均收益率分別為-33.6517%和-0.0448%，其他6個(gè)指數(shù)的總收益率和周均收益率均大于零。這表明，經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略遠(yuǎn)遠(yuǎn)優(yōu)于簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略。第二，7個(gè)指數(shù)中滬深300指數(shù)、中小板指數(shù)和創(chuàng)業(yè)板指數(shù)的收益率超過(guò)買入持有收益率，另外4個(gè)指數(shù)沒(méi)有戰(zhàn)勝買入持有策略。這表明，相對(duì)于簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略，經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略盡管有了顯著改善，但是其收益率仍然難以讓人滿意。

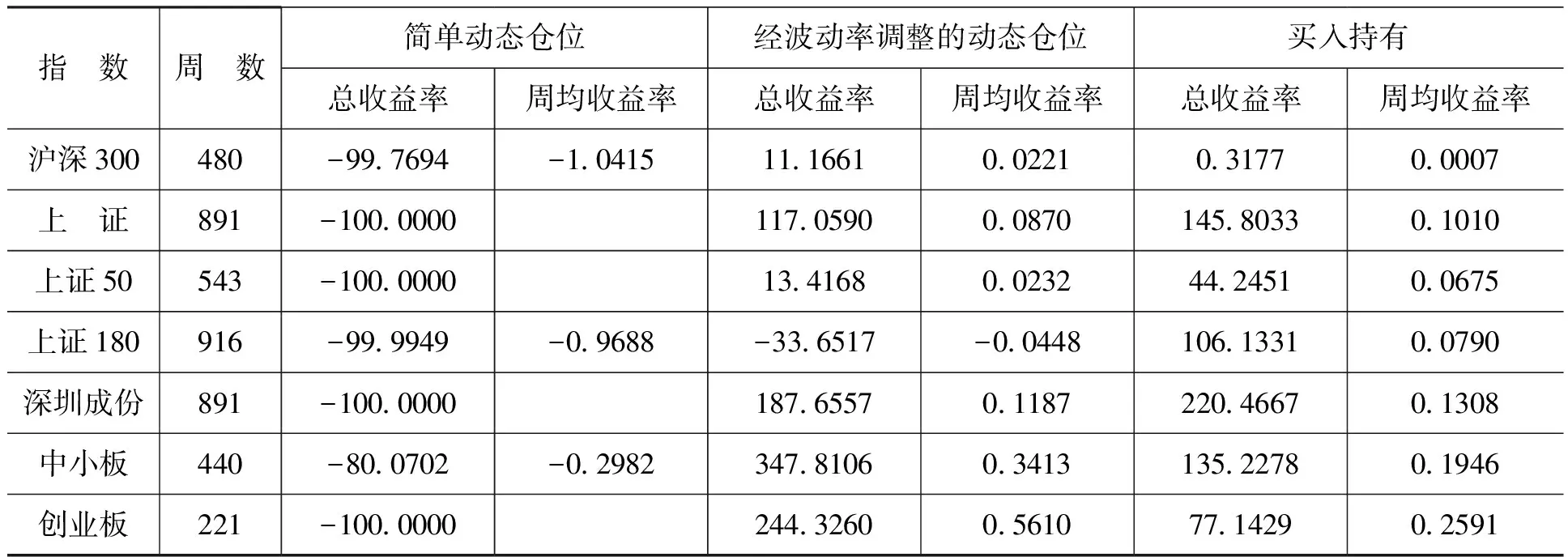
表3 動(dòng)態(tài)倉(cāng)位管理策略的收益率測(cè)算 單位：周，%

經(jīng)過(guò)仔細(xì)分析，筆者認(rèn)為，經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略之所以沒(méi)有獲得令人滿意的收益率，是因?yàn)槲覀冊(cè)谑?8)中根據(jù)波動(dòng)率大小以負(fù)線性相關(guān)的方式進(jìn)行了調(diào)整，無(wú)論什么原因，只要波動(dòng)率上升就降低倉(cāng)位，波動(dòng)率下降就提升倉(cāng)位。因此，這種調(diào)整方式?jīng)]有區(qū)分波動(dòng)率的變動(dòng)是來(lái)源于指數(shù)的大幅上漲還是大幅下跌，從而會(huì)引起指數(shù)大幅上漲時(shí)降低倉(cāng)位，進(jìn)而導(dǎo)致收益率的下跌。為了避免這一缺陷，在下文中我們擬根據(jù)來(lái)自技術(shù)分析方法的買賣信號(hào)增強(qiáng)的經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略。

(三)考慮買賣信號(hào)的經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略

均線系統(tǒng)顯示出金叉后股價(jià)指數(shù)通常會(huì)在均線的上方運(yùn)行，均線系統(tǒng)顯示出死叉后股價(jià)指數(shù)通常會(huì)在均線的下方運(yùn)行。借助這一規(guī)律，我們引入來(lái)自技術(shù)分析方法的買賣信號(hào)增強(qiáng)經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略。具體而言，均線處于多頭排列發(fā)出買入信號(hào)時(shí)應(yīng)該增加倉(cāng)位，均線處于空頭排列發(fā)出賣出信號(hào)時(shí)應(yīng)該減少倉(cāng)位。因此，我們將式(8)調(diào)整為：

fm=1+sign[(Dmax-D)/(Dmax-Dmin)]

(9)

其中，sign表示買賣信號(hào)，當(dāng)股價(jià)指數(shù)大于其均線值時(shí)sign=1，當(dāng)股價(jià)指數(shù)小于等于其均線值時(shí)sign=-1。

式(9)的含義是，當(dāng)股價(jià)指數(shù)在其均線的上方時(shí)根據(jù)波動(dòng)率的相對(duì)大小加倉(cāng)，當(dāng)股價(jià)指數(shù)在其均線的下方時(shí)根據(jù)波動(dòng)率的相對(duì)大小減倉(cāng)。為了便于比較，我們也考慮了買賣信號(hào)增強(qiáng)的簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略，即根據(jù)買賣信號(hào)直接確定簡(jiǎn)單動(dòng)態(tài)倉(cāng)位。具體地，當(dāng)均線處于多頭排列發(fā)出買入信號(hào)時(shí)倉(cāng)位為正(即做多)，均線處于空頭排列發(fā)出賣出信號(hào)時(shí)倉(cāng)位為負(fù)(即做空)。本文中，我們以5周均線為基準(zhǔn)，當(dāng)股價(jià)指數(shù)大于過(guò)去5周指數(shù)均值時(shí)根據(jù)式(9)加倉(cāng)，當(dāng)股價(jià)指數(shù)小于等于過(guò)去5周指數(shù)均值時(shí)根據(jù)式(9)減倉(cāng)。如表4所示。

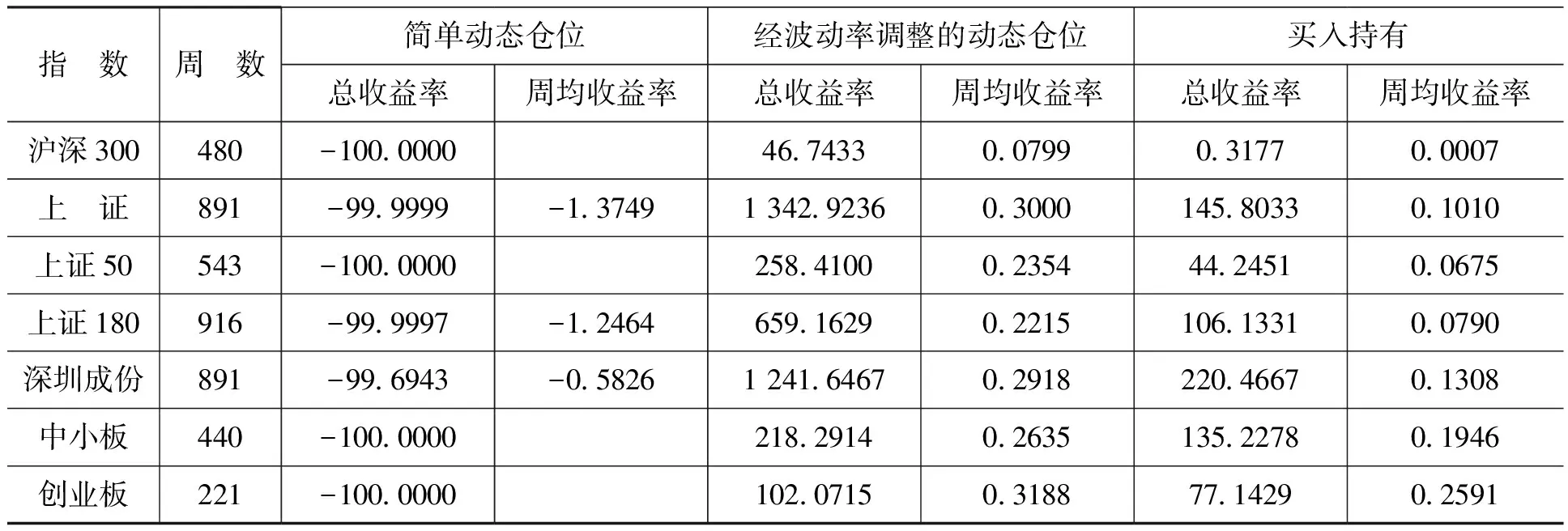
表4 買賣信號(hào)增強(qiáng)的動(dòng)態(tài)倉(cāng)位管理策略的收益率測(cè)算 單位：周，%

從表4可以看出，第一，考慮買賣信號(hào)增強(qiáng)的簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略與不考慮買賣信號(hào)增強(qiáng)的簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略一樣，其總收益率全部等于或接近-100%，考慮買賣信號(hào)并沒(méi)有提高倉(cāng)位管理的收益率。第二，買賣信號(hào)增強(qiáng)且經(jīng)波動(dòng)率調(diào)整后，7個(gè)指數(shù)的總收益率和周均收益率均顯著地高于買入持有的總收益率和周均收益率。這表明，買賣信號(hào)增強(qiáng)的經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略顯著地提高了倉(cāng)位管理的收益率。第三，相對(duì)于經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略，買賣信號(hào)增強(qiáng)的經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略對(duì)于中小板指數(shù)和創(chuàng)業(yè)板指數(shù)的倉(cāng)位管理效果有所下降。我們認(rèn)為，其原因可能在于中小板指數(shù)和創(chuàng)業(yè)板指數(shù)頻繁大幅波動(dòng)，相對(duì)于主板指數(shù)而言它們發(fā)出的買賣信號(hào)的可靠性較差，由此造成買賣信號(hào)增強(qiáng)的經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略不如不考慮買賣信號(hào)的經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略。

五、結(jié) 論

基于Kelly公式及其擴(kuò)展模型，本文在倉(cāng)位管理理論分析的基礎(chǔ)上，用中國(guó)A股市場(chǎng)7個(gè)主要指數(shù)(滬深300指數(shù)、上證指數(shù)、上證50指數(shù)、上證180指數(shù)、深圳成份指數(shù)、中小板指數(shù)和創(chuàng)業(yè)板指數(shù))對(duì)最優(yōu)倉(cāng)位估計(jì)和倉(cāng)位管理策略進(jìn)行了經(jīng)驗(yàn)分析。我們的研究結(jié)果表明：(1)中國(guó)A股市場(chǎng)中存在實(shí)現(xiàn)資產(chǎn)長(zhǎng)期增長(zhǎng)率最大化的最優(yōu)倉(cāng)位，進(jìn)行倉(cāng)位管理是有利可圖的。因此，作為資產(chǎn)管理者和投資者應(yīng)該重視倉(cāng)位管理，選擇適當(dāng)?shù)膫}(cāng)位管理策略尋求最優(yōu)倉(cāng)位，以實(shí)現(xiàn)資產(chǎn)長(zhǎng)期增長(zhǎng)的最大化。(2)倉(cāng)位管理的額外回報(bào)源于其高杠桿。交易杠桿具有兩面性，選擇適當(dāng)?shù)母軛U能夠提高資產(chǎn)的長(zhǎng)期增長(zhǎng)率，杠桿過(guò)高或者過(guò)低均會(huì)阻礙或損壞資產(chǎn)的長(zhǎng)期增長(zhǎng)。(3)簡(jiǎn)單動(dòng)態(tài)倉(cāng)位管理策略無(wú)法達(dá)到最優(yōu)倉(cāng)位，會(huì)造成資產(chǎn)的重大損失。中國(guó)A股市場(chǎng)仍然處于結(jié)構(gòu)變化和逐漸完善之中，投資理念、投資方法和投資者情緒都在發(fā)展變化，這種情況下估計(jì)出一個(gè)與實(shí)際相近的最優(yōu)倉(cāng)位是較為困難的，因此，我們不能簡(jiǎn)單套用理論模型估計(jì)最優(yōu)倉(cāng)位，必須要根據(jù)市場(chǎng)波動(dòng)規(guī)律調(diào)整最優(yōu)倉(cāng)位估計(jì)值。(4)經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略能夠顯著提高資產(chǎn)增長(zhǎng)率，但不能完全戰(zhàn)勝買入持有策略。大量經(jīng)驗(yàn)證據(jù)顯示波動(dòng)率具有預(yù)測(cè)性，波動(dòng)率的這種預(yù)測(cè)性具有一定的應(yīng)用價(jià)值，本文的經(jīng)驗(yàn)證據(jù)也顯示出波動(dòng)率可以被用來(lái)改善倉(cāng)位管理。(5)用買賣信號(hào)增強(qiáng)的經(jīng)波動(dòng)率調(diào)整的動(dòng)態(tài)倉(cāng)位管理策略能夠完勝買入持有策略，尤其是對(duì)偏重于大市值的指數(shù)。

[1] Kelly, J.L.A New Interpretation of Information Rate[J].Bell System Technical Journal, 1956,35(1):917-926.

[2] Thorp, E.O.The Kelly Criterion in Blackjack Sports Betting and the Stock Market[J].Hand-Book of Asset and Liability Management, 2006, 11(1):387-428.

[3] Samuelson, P.A.Lifetime Portfolio Selection by Dynamic Stochastic Programming[J].Review of Economics and Statistics, 1969, 51(3):239-246.

[4] Hakansson, N.H.Optimal Investment and Consumption Strategies Under Risk for a Class of Utilities Functions[J].Econometrica, 1970, 38(5):587-607.

[5] Merton, R.C., Samuelson, P.A.Fallacy of the Log-Normal Approximation to Optimal Portfolio Decision-Making Over Many Periods[J].Journal of Financial Economics, 1974, 11(1):67-94.

[6] Miller, B.L.Optimal Portfolio Decision Making Where the Horizon Is Infinite[J].Management Science, 1975, 22(2):220-225.

[7] Aucamp, D.On the Extensive Number of Plays to Achieve Superior Performance With the Geometric Mean Strategy[J]. Management Science, 1993, 39(9):1163-1172.

[8] Maclean, L.C., Thorp, E.O.，Zhao, W.T.，et al.Medium Term Simulations of the Full Kelly and Fractional Kelly Investment Strategies[J].The Kelly Capital Growth Investment Criterion: Theory and Practice, 2010, 11(2):543-562.

[9] Maslov, S.，Zhang, Y.C.Optimal Investment Strategy for Risky Assets[J].International Journal of Theoretical and Applied Finance, 1998, 1(3):377-387.

[10] Medo, M., Pis’Mak, Y.M., Zhang, Y.C.Diversification and Limited Information in the Kelly Game[J].Physica A Statistical Mechanics & Its Application, 2008, 387(24): 6151-6158.

[11] Medo, M., Zhang, Y.C.How to Quantify the Influence of Correlations on Investment Diversification[J].International Review of Financial Analysis, 2009, 18(1-2):34-39.

[12] Samuelson, P.A.Why We Should not Make Mean Log of Wealth Big Though Years to Act Are Long[J].Journal of Banking and Finance, 1979, 3(4):305-307.

[13] Rotando, L.M., Thorp, E.O.The Kelly Criterion and the Stock Market[J].The American Mathematical Monthly, 1992, 99(10):922-931.

[14] Maclean, L.C., Ziemba, W.T., Blazenko, G.Growth Versus Security in Dynamic Investment Analysis[J].Management Science, 1992, 38(11):1562-1585.

[15] Anderson, J.A., Faff, R.W.Maximizing Futures Returns Using Fixed Fraction Asset Allocation[J].Applied Financial Economics, 2004, 14(15):1067-1073.

[16] 凌士勤.基于最優(yōu)增長(zhǎng)路徑的多期投資組合選擇及其動(dòng)態(tài)調(diào)整研究[D].武漢：華中科技大學(xué)博士學(xué)位論文, 2006.

[17] 羅勇.風(fēng)險(xiǎn)約束下的Kelly動(dòng)態(tài)投資組合優(yōu)化[D].成都：電子科技大學(xué)博士學(xué)位論文, 2015.

[18] Barroso, P., Santa-Clara, P.Momentum Has Its Moments[J].Journal of Financial Economics, 2015,116(1): 111-120.

2017-09-10

遼寧省社會(huì)科學(xué)規(guī)劃基金項(xiàng)目“金融沖擊、企業(yè)分散度與經(jīng)濟(jì)風(fēng)險(xiǎn)分析”(L15CJY005)

王志強(qiáng)(1965-)，男(蒙古族)，內(nèi)蒙古烏海人，教授，博士生導(dǎo)師，主要從事金融學(xué)、數(shù)量經(jīng)濟(jì)學(xué)等方面的研究。E-mail：wangzhiqiang@dufe.edu.cn張 聰(1989-)，男，遼寧大連人，博士研究生，主要從事金融工程研究。E-mail：zhangcongchuck@163.com

F832.1

A

1000-176X(2017)12-0037-08

巴紅靜)