電網(wǎng)畸變條件下的單相快速頻率自適應(yīng)鎖頻方案
貝太周,張博文
(1.國網(wǎng)山東省電力公司濟(jì)南供電公司,山東 濟(jì)南 250012;2.天津大學(xué)電氣自動化與信息工程學(xué)院,天津 300072)
電網(wǎng)畸變條件下的單相快速頻率自適應(yīng)鎖頻方案
貝太周1,張博文2
(1.國網(wǎng)山東省電力公司濟(jì)南供電公司,山東 濟(jì)南 250012;2.天津大學(xué)電氣自動化與信息工程學(xué)院,天津 300072)
分布式并網(wǎng)逆變器的同步控制和主動式孤島檢測需要電網(wǎng)基波頻率的準(zhǔn)確檢測。為了提高在電網(wǎng)畸變環(huán)境下頻率檢測的準(zhǔn)確性,基于單相分布式并網(wǎng)系統(tǒng),提出一種能夠在電網(wǎng)畸變條件下具有快速動態(tài)響應(yīng)的頻率自適應(yīng)鎖頻方案。在該方案中,借助所提的改進(jìn)型正交信號發(fā)生器和級聯(lián)復(fù)數(shù)濾波網(wǎng)絡(luò)分別實(shí)現(xiàn)直流分量和諧波擾動的有效消除和抑制。為保證所提方案在頻率突變情形下仍然具有精準(zhǔn)的性能,在αβ坐標(biāo)系下構(gòu)造了具有快速動態(tài)響應(yīng)的頻率自適應(yīng)控制器,實(shí)現(xiàn)對電網(wǎng)基波頻率的快速跟蹤。方案的可行性通過仿真及實(shí)驗(yàn)結(jié)果得到驗(yàn)證。
電網(wǎng)同步;并網(wǎng)逆變器;諧波抑制;復(fù)數(shù)濾波器;頻率自適應(yīng)控制
0 引言
可再生能源具有更加清潔、更加可靠和產(chǎn)能靈活等突出優(yōu)勢[1-2],依托可再生能源建立發(fā)展起來的分布式發(fā)電已經(jīng)高比例滲透到傳統(tǒng)的電力網(wǎng)絡(luò)。作為分布式發(fā)電系統(tǒng)和電力網(wǎng)絡(luò)之間的接口,電力電子設(shè)備、信息通信等技術(shù)將會在未來的電力網(wǎng)絡(luò)中被廣泛采用。電力電子設(shè)備的不斷滲透引起人們對交流電能質(zhì)量和電網(wǎng)穩(wěn)定性的密切關(guān)注[2]。為了保證電力網(wǎng)絡(luò)的高效穩(wěn)定運(yùn)行,應(yīng)務(wù)必對分布式發(fā)電系統(tǒng)中的并網(wǎng)逆變器給予精心設(shè)計(jì)和精確控制。
為了保證并網(wǎng)逆變器能夠向電網(wǎng)輸送高質(zhì)量的交流電能,就需要為其配置強(qiáng)勁穩(wěn)健的技術(shù)支持。其中涉及并網(wǎng)逆變器控制的一個關(guān)鍵技術(shù)便是同步鎖頻技術(shù)。通過該技術(shù)獲取的電網(wǎng)頻率信息,可以用于并網(wǎng)逆變器的同步控制和主動式孤島檢測,一旦無法獲取準(zhǔn)確的電網(wǎng)頻率信息,將會危及分布式發(fā)電系統(tǒng)的安全運(yùn)行。實(shí)際應(yīng)用中,常因電網(wǎng)暫態(tài)故障、電壓測量及轉(zhuǎn)換等原因引入一定量的直流分量[3],同時真實(shí)電網(wǎng)環(huán)境中的諧波擾動[4]、頻率突變[5]等情況均會阻礙電網(wǎng)頻率信息的準(zhǔn)確獲取。
用于消除直流分量、抑制諧波擾動的電壓同步技術(shù)在近期文獻(xiàn)中被不斷提出。在消除直流分量影響方面,均值誤差補(bǔ)償法[3]、積分反饋補(bǔ)償法[6-7]以及dq坐標(biāo)系下的交直流分量分離法[8]雖能有效消除直流分量,但是這些方法都是在傳統(tǒng)結(jié)構(gòu)的基礎(chǔ)上通過引入其他結(jié)構(gòu)單元來實(shí)現(xiàn)的,這在一定程度上增大了系統(tǒng)結(jié)構(gòu)的復(fù)雜度和同步鎖頻的運(yùn)算量。研究一種具有結(jié)構(gòu)簡單,可有效消除直流分量影響的同步鎖頻方案顯得尤為重要。
在諧波抑制方面,借助復(fù)數(shù)濾波器進(jìn)行多通道諧波解耦及補(bǔ)償在近期文獻(xiàn)中備受推崇[2,4,7]。 此種方法的核心在于對電網(wǎng)環(huán)境中存在較多的某次諧波分通道地進(jìn)行無衰減提取,然后將提取到的諧波反饋補(bǔ)償?shù)诫娋W(wǎng)電壓采樣信號中,即對某一諧波采用“先提取后補(bǔ)償”的方式進(jìn)行高效抑制。然而這類方法僅適用于諧波組成相對穩(wěn)定的電網(wǎng)環(huán)境,當(dāng)電網(wǎng)諧波畸變嚴(yán)重時,諧波抑制性能將大為受損。盡管可以通過添加通道數(shù)目的方法來加以改善,但是此種方法無疑又會增加系統(tǒng)實(shí)現(xiàn)的復(fù)雜度[9]。因此,如何保證濾波器能夠在諧波畸變嚴(yán)重的電網(wǎng)環(huán)境下最大頻率范圍地抑制諧波是濾波器設(shè)計(jì)和實(shí)現(xiàn)時必須要考慮的問題。
本文將以單相系統(tǒng)的同步鎖頻技術(shù)為背景,首先提出一種兼具消除直流分量的新型正交信號發(fā)生器,然后基于復(fù)數(shù)濾波器構(gòu)建了一種對各次諧波具有深度衰減作用的級聯(lián)濾波網(wǎng)絡(luò)。為了保證整個鎖頻系統(tǒng)能夠在頻率突變的電網(wǎng)環(huán)境中仍可以快速實(shí)現(xiàn)對電網(wǎng)頻率的及時跟蹤與鎖定,在αβ坐標(biāo)系下提出了一種不受電壓波動影響的頻率自適應(yīng)控制器,文章最后對所提方案的可行性進(jìn)行了仿真和實(shí)驗(yàn)驗(yàn)證。
1 可消除直流分量的改進(jìn)型SOGI-QSG
圖1所示的SOGI-QSG (Second Order Generalized Integrator based on Quadrature Signal Generator)方案易實(shí)現(xiàn)、運(yùn)算量少[10-17],因此在單相同步鎖頻方案中得到廣泛應(yīng)用。圖中,k和ωo分別為SOGI-QSG的增益和中心頻率。當(dāng)中心頻率ωo等于實(shí)際的電網(wǎng)基波頻率ω時,SOGI-QSG可用于正交信號的產(chǎn)生[7]。
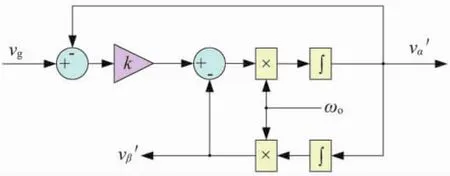
圖1 SOGI-QSG結(jié)構(gòu)
SOGI-QSG的特征傳遞函數(shù)為
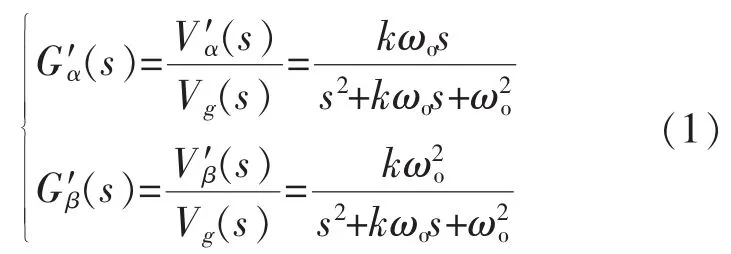
僅考慮直流分量影響,定義含有直流分量的電網(wǎng)電壓vg為

式中:V、ω、vdc分別為電網(wǎng)電壓的幅值、基波角頻率和直流分量。
將式(2)中的直流分量vdc視為頻率為0的交流量[8],在穩(wěn)態(tài)情況下(ωo=ω),SOGI-QSG 的輸出為
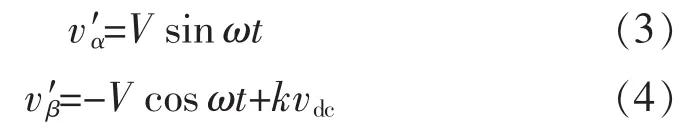
結(jié)合式(3)和式(4),當(dāng)電網(wǎng)電壓 vg混有直流分量時,SOGI-QSG 的輸出電壓 v′α和 v′β因 v′β內(nèi)含有直流成分kvdc而無法嚴(yán)格正交,因此SOGI-QSG結(jié)構(gòu)不具有消除直流分量的功能。針對這一不足,提出一種可消除直流分量的改進(jìn)型SOGI-QSG。結(jié)合式(2)和式(3),穩(wěn)態(tài)時,由 SOGI-QSG產(chǎn)生的電壓分量 v′α可理解為式(2)中電網(wǎng)電壓vg的交流分量,因此vg中的直流分量vdc在數(shù)值上又可表示為

將式(5)代入式(4),移項(xiàng)整理后得到
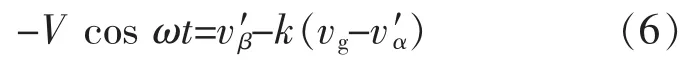
因此,若期望改進(jìn)的SOGI-QSG在穩(wěn)態(tài)時得到vα=V sin ωt及 vβ=V cos ωt的正交電壓對,可令
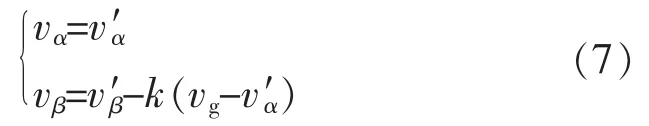
基于圖1和式(7)建立起的改進(jìn)型SOGI-QSG結(jié)構(gòu)如圖2所示。
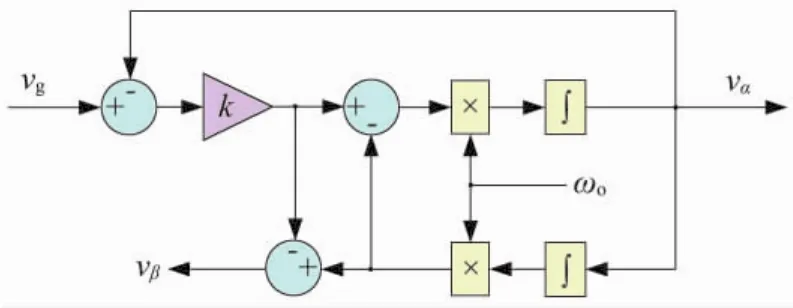
圖2 改進(jìn)型SOGI-QSG結(jié)構(gòu)
相應(yīng)的特征傳遞函數(shù)為
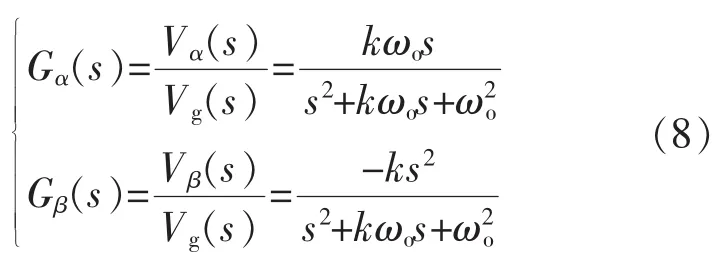
穩(wěn)態(tài)時,式(2)所描述的電網(wǎng)電壓vg經(jīng)改進(jìn)型SOGI-QSG后得到的任意時刻t時的電壓輸出為
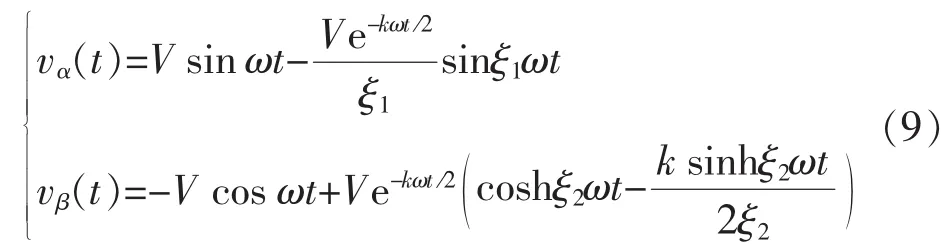
為使 vα(t)中的 sinξ1ωt在實(shí)數(shù)范圍內(nèi)有意義,應(yīng)滿足0<k<2。在該范圍內(nèi)對k進(jìn)行合理取值,即可保證 e-kωt/2在有限短的時間內(nèi)快速收斂于 0, 此時vα(t)和 vβ(t)進(jìn)一步簡化為

式(10)表明,借助改進(jìn)型SOGI-QSG可以得到一對嚴(yán)格正交的輸出電壓vα和vβ。另外,與SOGIQSG相比較,改進(jìn)型SOGI-QSG并未添加輔助單元,因此改進(jìn)方案具有結(jié)構(gòu)簡單、運(yùn)算量少的顯著優(yōu)勢。
關(guān)于k值的選定。k值同時影響著SOGI-QSG響應(yīng)輸出的調(diào)整時間和動態(tài)響應(yīng)超調(diào):當(dāng)k取值較大時,調(diào)節(jié)時間縮短,超調(diào)量增大;當(dāng)k取值較小時,調(diào)節(jié)時間延長,超調(diào)量減小;k取時可保證調(diào)整時間和動態(tài)響應(yīng)超調(diào)之間關(guān)系最優(yōu)[18]。
2 級聯(lián)復(fù)數(shù)濾波網(wǎng)絡(luò)
實(shí)際電網(wǎng)中的諧波擾動常常影響鎖頻性能[6]。為了保證鎖頻方案在諧波擾動下仍具有良好的性能,必須采取積極有效的措施來降低電網(wǎng)諧波的影響。
鑒于直流分量可在改進(jìn)型SOGI-QSG內(nèi)有效消除,故此處不對其予以分析。定義含有諧波擾動的電網(wǎng)電壓vg為
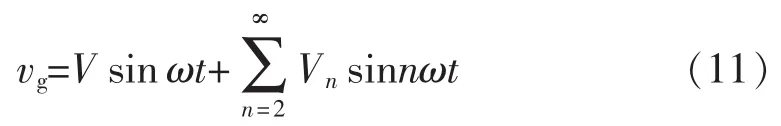
式中:n為諧波次數(shù);Vn為n次諧波電壓的幅值。
由式(8)可知,穩(wěn)態(tài)時,改進(jìn)型SOGI-QSG對自身輸出電壓vα和vβ中各次電網(wǎng)諧波的幅值和相位的影響用極坐標(biāo)表示為
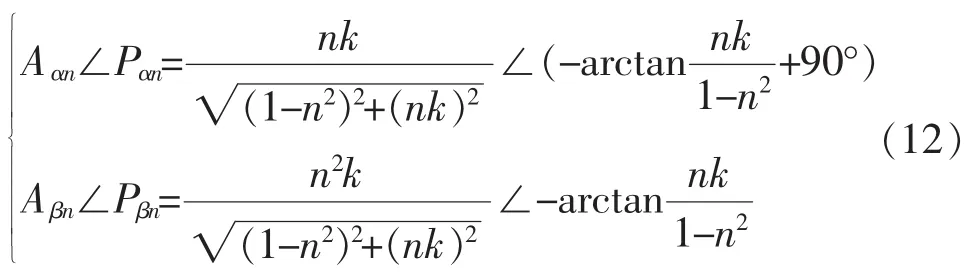
穩(wěn)態(tài)時,式(11)所描述的電網(wǎng)電壓vg經(jīng)改進(jìn)型SOGI-QSG后,得到的輸出電壓為
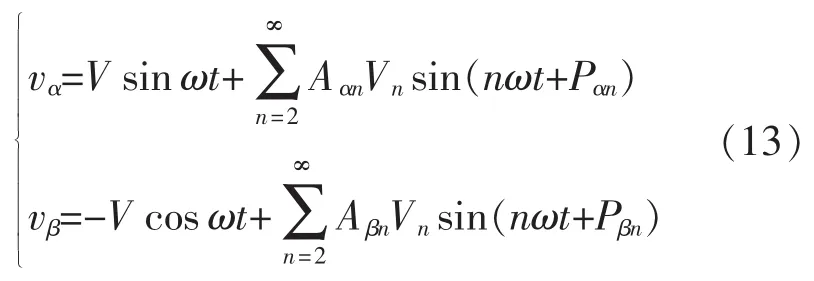
據(jù)式(13)可知,由于電網(wǎng)諧波的影響,電壓分量vα和vβ中仍然含有相當(dāng)量的各次諧波。為了保證鎖頻方案在諧波擾動條件下表現(xiàn)出良好的精度,應(yīng)當(dāng)最大限度地抑制vα和vβ中的各次諧波。
2.1 自適應(yīng)復(fù)數(shù)濾波器
為了能夠有效抑制電網(wǎng)諧波帶來的影響,基于式(14)所描述的自適應(yīng)復(fù)數(shù)濾波器(Adaptive Complex Filter,ACF)建立一種簡單有效的濾波方案。
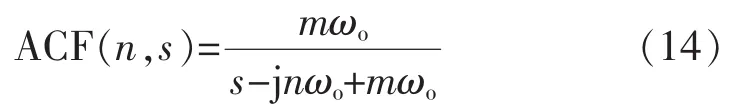
式中:m為ACF的增益;n為諧波次數(shù);nωo構(gòu)成了ACF對應(yīng)于n次諧波時的中心頻率。
在αβ坐標(biāo)系下,復(fù)數(shù)因子j可通過交叉耦合方式實(shí)現(xiàn)[18]。因此,ACF的實(shí)現(xiàn)框圖如圖3所示。圖中,vαi、vβi和 vαo、vβo分別為 ACF 的輸入和輸出。
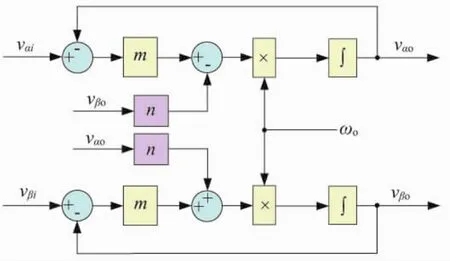
圖3 ACF的實(shí)現(xiàn)
考查ACF的幅—相特性,其特性方程為
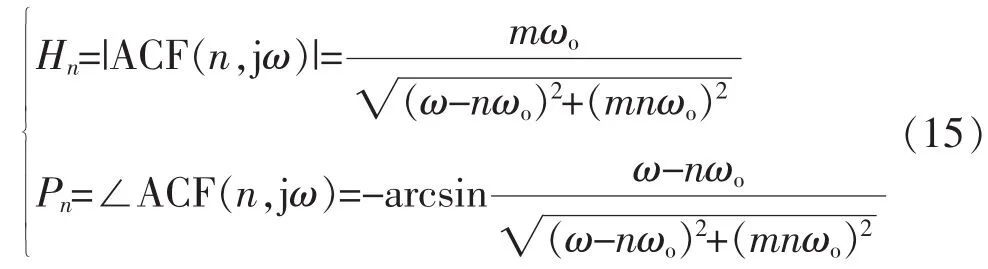
當(dāng) ωo=100π rad/s時,根據(jù)式(15),可以繪出ACF在(n,m)不同取值時的Bode圖,如圖4所示。根據(jù)該Bode圖可知,n主要決定著ACF中心頻率的位置,而m則影響著ACF帶寬的寬度。
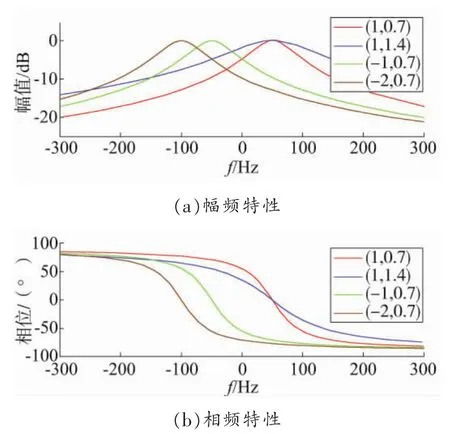
圖4 (n,m)不同值時ACF的Bode圖
觀察圖4發(fā)現(xiàn),當(dāng)n為負(fù)值時,ACF對電網(wǎng)中的各頻率信號均有幅值衰減和相位偏移的影響,這種影響將隨著負(fù)數(shù)n的減小而不斷增強(qiáng);而當(dāng)n為正值時,ACF除了對自身的中心頻率信號無任何影響外,對其他頻率的信號將有不同程度的幅值衰減和相位偏移。特別地,當(dāng)n取值為1時,借助某些控制策略,即可實(shí)現(xiàn)對電網(wǎng)基波頻率的無差跟蹤。
為分析簡便起見,僅考慮ACF在n=±1時構(gòu)成的級聯(lián)濾波網(wǎng)絡(luò)(Cascaded Filtering Network,CFN),網(wǎng)絡(luò)結(jié)構(gòu)如圖5所示。

圖5 由ACFs構(gòu)成的級聯(lián)濾波網(wǎng)絡(luò)
2.2 參數(shù)設(shè)定
根據(jù)圖5所示的CFN,可知其傳遞函數(shù)為
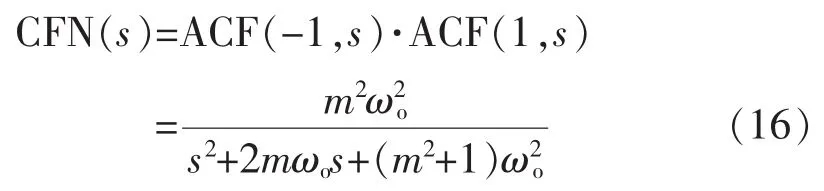
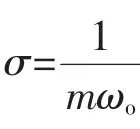

另外,由式(16)可知,增益m在數(shù)值上等于該二階系統(tǒng)的阻尼比,因此,CFN單位階躍響應(yīng)的超調(diào)量為
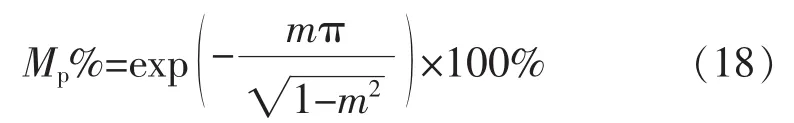
圖6給出在ωo=100π rad/s以及不同m值情況下的式(16)所示的CFN的單位階躍響應(yīng)。
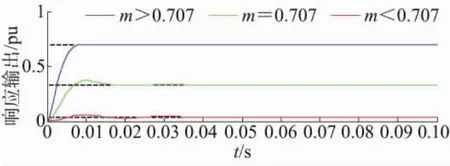
圖6 不同m值情況下CFN的單位階躍響應(yīng)
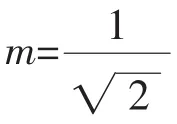
2.3 諧波抑制分析
穩(wěn)態(tài)時,結(jié)合式(12)和式(15)中的 Hn以及已經(jīng)確定的 k、m 值, 可以得到電壓分量 vα1和 vβ1、vα2和vβ2中n次諧波的幅值衰減系數(shù),分別如式(19)和式(20)所示。
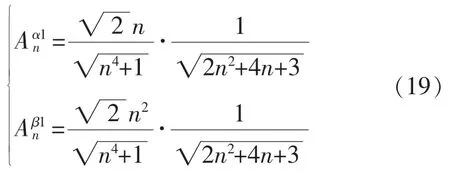
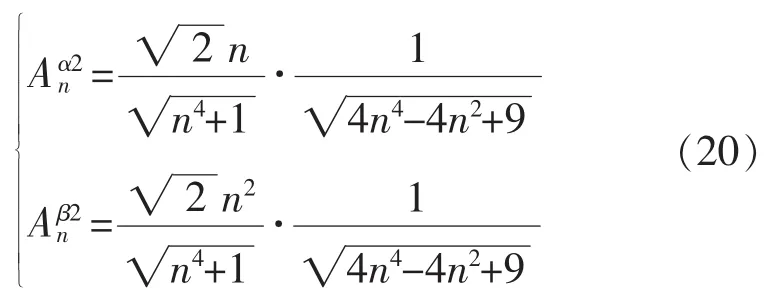
基于式(19)和式(20),圖7給出了級聯(lián)濾波網(wǎng)絡(luò)對電壓分量 vα1、vβ1和 vα2、vβ2中各次諧波的幅值衰減系數(shù)分布。
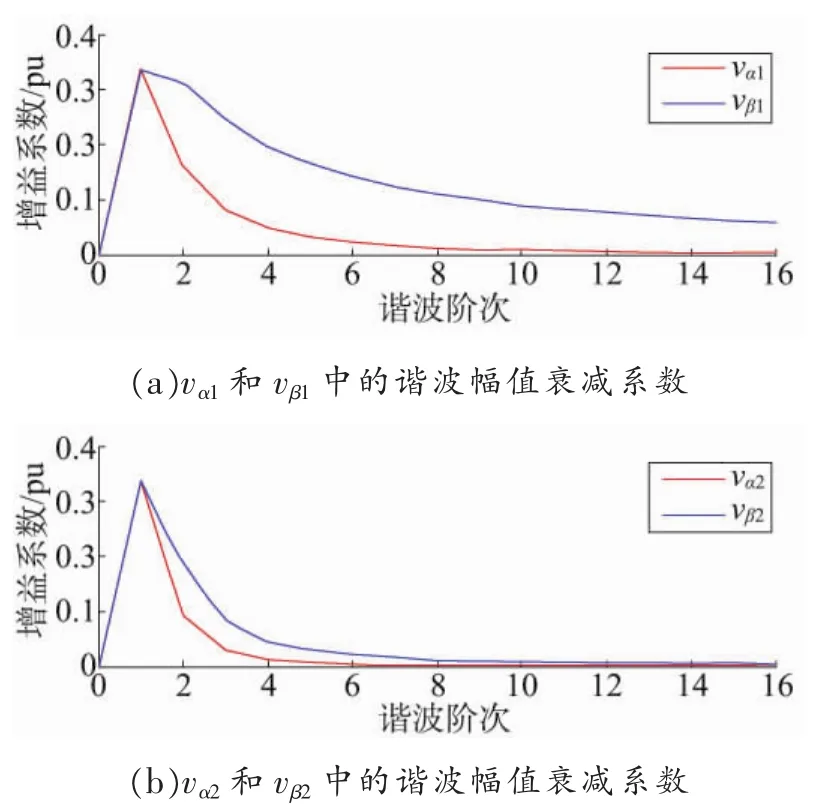
圖7 CFN對諧波的抑制
觀察圖7可以發(fā)現(xiàn),基于式(14)所示的自適應(yīng)復(fù)數(shù)濾波器 ACF(-1,s)和 ACF(1,s)均可以為 vα1、vβ1和 vα2、vβ2中的各次諧波提供不同程度的幅值衰減系數(shù),并且諧波的次數(shù)越高,提供的幅值衰減系數(shù)越小。
EN50160標(biāo)準(zhǔn)對公共配電系統(tǒng)中的電壓質(zhì)量做出了相關(guān)規(guī)定。按照此標(biāo)準(zhǔn),電網(wǎng)中的各次諧波分量不能超出最大容許限值。考慮本文所提方案對電網(wǎng)電壓中的各次諧波有很好的抑制能力,而對基波分量的影響很小,因此在進(jìn)行頻率自適應(yīng)控制器的設(shè)計(jì)時僅考慮基波分量。
3 具有快速動態(tài)響應(yīng)的頻率自適應(yīng)控制器
根據(jù)前文所述,當(dāng)中心頻率ωo等于電網(wǎng)基波頻率ω時,改進(jìn)型SOGI-QSG以及級聯(lián)濾波網(wǎng)絡(luò)可以保證良好的動態(tài)響應(yīng)和濾波性能,考慮到實(shí)際電網(wǎng)存在頻率突變的情形,應(yīng)務(wù)求對實(shí)際電網(wǎng)基波頻率進(jìn)行快速準(zhǔn)確跟蹤,并及時調(diào)整中心頻率,使兩者趨于一致。
圖5中,由改進(jìn)型SOGI-QSG產(chǎn)生的電壓分量vα和 vβ依次經(jīng)過 ACF(-1,s)和 ACF(1,s)濾波后,輸出電壓 vα1、vβ1和 vα2、vβ2,分別表示為
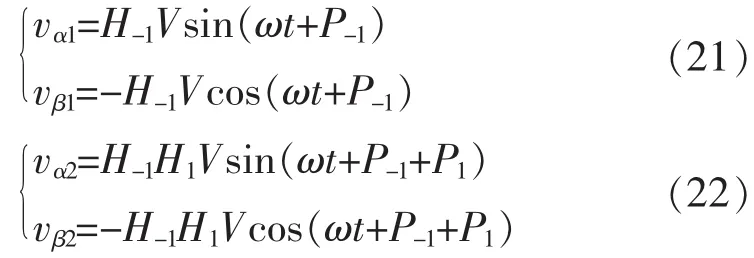
設(shè)計(jì)頻率自適應(yīng)控制器的調(diào)整律為
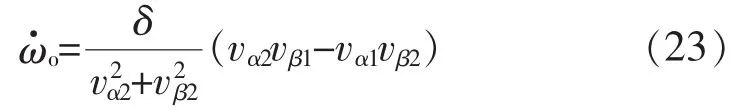
式中:δ為頻率自適應(yīng)調(diào)整系數(shù)。
將式(21)、式(22)同時代入式(23),可以得到
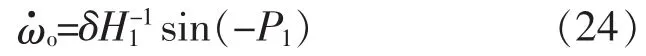
由于式(24)中不含H-1及P-1,因此,在整個鎖頻方案中,ACF(-1,s)僅起到濾波的作用,而對頻率自適應(yīng)控制器的調(diào)整律沒有任何影響。特別地,當(dāng)中心頻率ωo無限接近于電網(wǎng)基波頻率ω時,結(jié)合式(15)以及m的預(yù)設(shè)值,可將式(24)進(jìn)一步化簡為
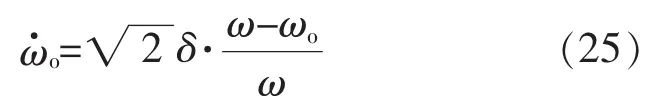
頻率自適應(yīng)的動態(tài)調(diào)節(jié)過程可描述為:當(dāng)ω>ωo時,根據(jù)式(25)可及時調(diào)整 ωo線性增大;當(dāng) ω<ωo時,可及時調(diào)整ωo線性減小;當(dāng)ωo經(jīng)過自適應(yīng)調(diào)整等于ω時,ωo保持不變。因此,頻率自適應(yīng)調(diào)整律的實(shí)質(zhì)在于:當(dāng)電網(wǎng)基波頻率ω改變時,迫使鎖頻輸出ωo朝著消除這種改變的方向移動,直到ωo收斂于ω。
為了評估式(25)所描述的頻率自適應(yīng)調(diào)整的動態(tài)響應(yīng)速度,定義用于檢測頻率響應(yīng)的時間常數(shù)τ為

式(26)表明,在頻率自適應(yīng)調(diào)整系數(shù)δ一定的情況下,時間常數(shù)τ僅與電網(wǎng)頻率ω成正比,而與電網(wǎng)幅值無關(guān)。因此,由式(23)確定的頻率自適應(yīng)調(diào)整律保證了整個鎖頻系統(tǒng)在頻率調(diào)整的響應(yīng)時間上不受實(shí)際電網(wǎng)中電壓波動的影響。
按照電網(wǎng)接入標(biāo)準(zhǔn)的要求,分布式并網(wǎng)逆變器應(yīng)在 47~52 Hz的頻率范圍內(nèi)運(yùn)行[17],考慮到頻率的小幅變化對頻率自適應(yīng)調(diào)整的動態(tài)響應(yīng)速度和時間常數(shù)的影響十分有限,因此在借助式(26)確定頻率自適應(yīng)調(diào)整系數(shù)δ時,電網(wǎng)基波頻率ω可取100π rad/s。
4 仿真及實(shí)驗(yàn)驗(yàn)證
為了驗(yàn)證本文所提的改進(jìn)型SOGI-QSG的響應(yīng)性能,將QSG的中心頻率ωo設(shè)置為2π50 rad/s,輸入信號選用20 V/50 Hz的交流信號混合1 V的直流偏置。輸出電壓的仿真結(jié)果如圖8所示。觀察圖8可以發(fā)現(xiàn),改進(jìn)型SOGI-QSG經(jīng)過20 ms的動態(tài)調(diào)整過程,穩(wěn)定輸出后電壓分量vα和vβ中不再含有直流分量,vα和vβ嚴(yán)格正交。仿真結(jié)果顯示了所提出的改進(jìn)型SOGI-QSG結(jié)構(gòu)可以簡單有效地消除輸入信號中的直流分量,快速構(gòu)建正交電壓。
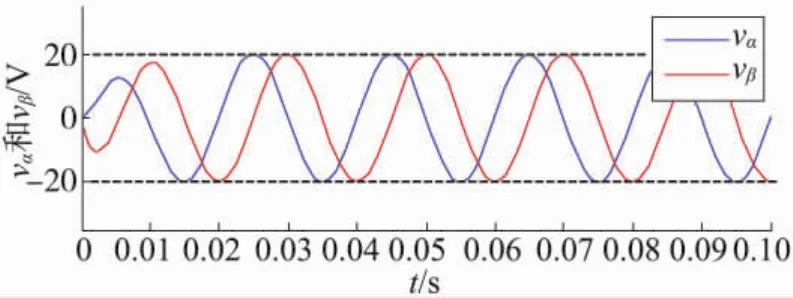
圖8 改進(jìn)型SOGI-QSG的響應(yīng)
關(guān)于頻率自適應(yīng)調(diào)整律的驗(yàn)證,仿真中相關(guān)參數(shù)設(shè)置如下:用20 V/50 Hz的交流信號來模擬實(shí)際的電網(wǎng)電壓,時間常數(shù)τ設(shè)置為20 ms,在t=0.04 s時刻,電網(wǎng)基波頻率由50 Hz瞬間變?yōu)?0 Hz。為了體現(xiàn)出該方案的動態(tài)響應(yīng)性能,特將其與文獻(xiàn)[19]中所研究的傳統(tǒng)SOGI-FLL方案在同等條件下進(jìn)行比較,所得的仿真結(jié)果如圖9所示。據(jù)圖9可以看出,當(dāng)實(shí)際的電網(wǎng)頻率發(fā)生突變時,采用本文所提方案,經(jīng)過10 ms時間可以快速鎖定當(dāng)前的頻率,而采用傳統(tǒng)SOGI-FLL方案則需要40 ms。因此,所提方案具有更快的動態(tài)響應(yīng)速度。
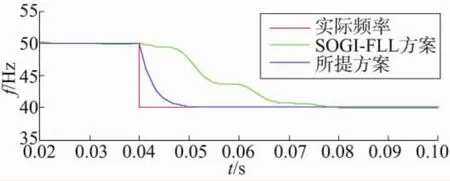
圖9 頻率自適應(yīng)調(diào)整的動態(tài)響應(yīng)
在實(shí)驗(yàn)室條件下,由可編程交流電源提供的幅值為20 V、頻率為50 Hz的交流信號疊加1 V的直流偏置來模擬電網(wǎng)基波電壓,QSG的電壓增益k為。運(yùn)算處理器芯片采用型號為TMS320F28335的DSP,采樣頻率為10 kHz。圖10給出了采用改進(jìn)型SOGI-QSG產(chǎn)生的正交電壓vα和vβ的波形圖。從波形圖上能夠看出:大約經(jīng)過20 ms的調(diào)整,可以得到穩(wěn)定的正交電壓 vα與 vβ。 輸出穩(wěn)定后,vα與 vβ之間在相位上存在90°的相位差,而在幅值上,兩者之間幅值相同,正負(fù)半周各自對稱。
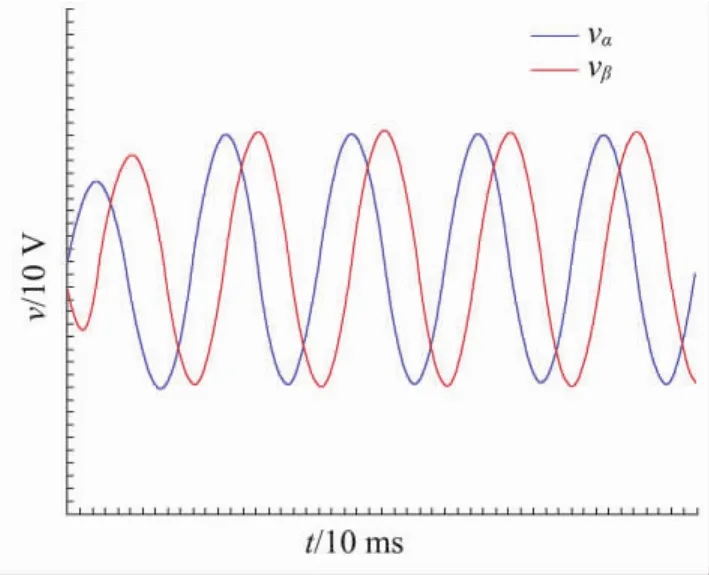
圖10 正交電壓實(shí)驗(yàn)波形
為了驗(yàn)證本文所提的頻率自適應(yīng)調(diào)整律的動態(tài)響應(yīng),初始輸入信號中的基波分量采用幅值為20 V、頻率為50 Hz的交流信號,諧波分量按表1取值。
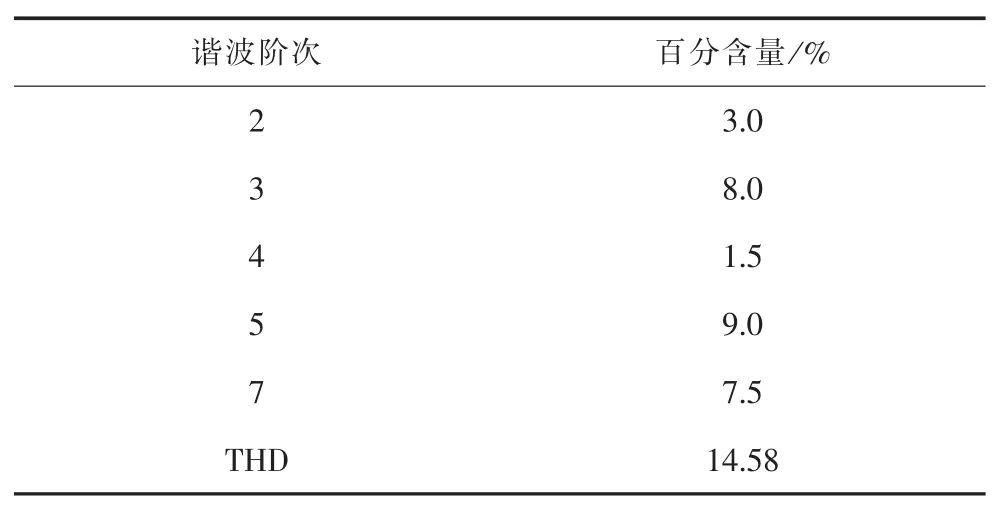
表1 諧波抑制測試中注入的諧波含量及THD
頻率變化設(shè)定為由50 Hz突變到40 Hz。時間常數(shù)τ均設(shè)定為20 ms。為了驗(yàn)證幅值變化對鎖頻性能的影響,實(shí)驗(yàn)中設(shè)定兩種幅值變化:幅值始終保持不變;在頻率突變前幅值由20 V跌落為16 V。實(shí)驗(yàn)波形如圖11所示。
由圖11可知,當(dāng)輸入信號的頻率減小時,若采用式(23)所示的頻率自適應(yīng)調(diào)整方案,無論輸入電壓是否發(fā)生波動,均不會對頻率調(diào)整產(chǎn)生任何影響,在10 ms的時間范圍內(nèi)即可完成對頻率的自適應(yīng)調(diào)整與鎖定。
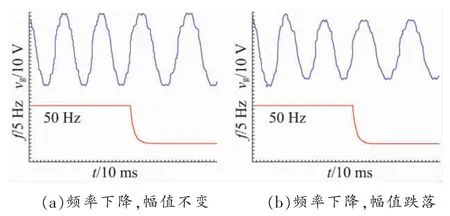
圖11 頻率變化時鎖頻方案的實(shí)驗(yàn)波形
5 結(jié)語
在考慮存在直流分量、諧波擾動和頻率突變的電網(wǎng)畸變條件下,提出了一種可有效消除直流分量影響并抑制諧波畸變的單相頻率自適應(yīng)鎖頻方案。該方案能夠有效消除直流分量和抑制電網(wǎng)諧波,同時快速的動態(tài)響應(yīng)性能能夠保證自身在較短的時間內(nèi)快速鎖定當(dāng)前時刻的電網(wǎng)頻率。總體方案具有結(jié)構(gòu)簡單、參數(shù)設(shè)置少、動態(tài)性能好等優(yōu)點(diǎn)。可行性和有效性最后通過仿真和實(shí)驗(yàn)得以驗(yàn)證。
[1]VAZQUEZ S,SANCHEZ J A,REYES M R,et al.Adaptive vectorial filter for grid synchronization of power converters under unbalanced and/or distorted grid conditions[J].IEEE Transactions on Industrial Electronics,2014,61(3):1 355-1 367.
[2]MATAS J,CASTILLA M,MIRET J,et al.An adaptive prefiltering method to improve the speed/accuracy tradeoff of voltage sequence detection methods under adverse grid conditions[J].IEEE Transactions on Industrial Electronics,2014,61(5):2 139-2 151.
[3]HWANG S H,LIU L M,LI H,et al.DC offset error compensation for synchronous reference frame PLL in single-phase grid-connected converters[J].IEEE Transactions on Power Electronics,2012,27(8):3 467-3 471.
[4]杜雄,王國寧,孫鵬菊,等.兩相靜止坐標(biāo)系下消除不對稱和諧波影響的同步信號提取方法[J].電工技術(shù)學(xué)報(bào),2015,30(4):249-256.
[5]汪飛,毛華龍,許德志,等.多變電網(wǎng)條件下的對稱序列與諧波檢測[J].電工技術(shù)學(xué)報(bào),2014,29(12):158-165.
[6]王德玉,劉文釗,郭小強(qiáng),等.非理想電網(wǎng)電壓情況下并網(wǎng)變換器高階解耦復(fù)數(shù)濾波并網(wǎng)同步技術(shù)[J].中國電機(jī)工程學(xué)報(bào),2015,35(10):2 576-2 583.
[7]RODRIGUEZ P,LUNA A,CANDELA I,et al.Multiresonant frequency-locked loop for grid synchronization of power converters under distorted grid conditions[J].IEEE Transactions on Industrial Electronics,2011,58(1):127-138.
[8]杜雄,劉延?xùn)|,孫鵬菊,等.消除直流分量影響的并網(wǎng)變流器同步參考坐標(biāo)系鎖相環(huán)方法[J].電工技術(shù)學(xué)報(bào),2013,28(12):24-31.
[9]RODRIGUEZ P,LUNA A,MU OZ-AGUILAR R S,et al.A stationary reference frame grid synchronization system for threephase grid-connected power converters under adverse grid conditions[J].IEEE Transactions on Power Electronics,2012,27(1):99-112.
[10]THACKER T,BOROYEVICH D,BURGOS R,et al.Phase-locked loop noise reduction via phase detector implementation for singlephase systems[J].IEEE Transactions on Industrial Electronics,2011,58(6):2 482-2 490.
[11]REZA M S,CIOBOTARU M,AGELIDIS V G.Robust technique for accurate estimation of single-phase grid voltage fundamental frequency and amplitude[J].IET Generation,Transmission&Distribution,2015,9(2):183-192.
[12]辛振,趙仁德,郭寶玲,等.基于二階廣義積分器-鎖頻環(huán)的異步電機(jī)同步角頻率估計(jì)方法[J].電工技術(shù)學(xué)報(bào),2014,29(1):116-122.
[13]GHARTEMANI M K.A unifying approach to single-phase synchronous reference frame PLLs[J].IEEE Transactions on Power Electronics,2013,28(10):4 550-4 556.
[14]REZAM S,CIOBOTARU M,AGELIDIS V G.Accurate estimation of single-phase grid voltage parameters under distorted conditions[J].IEEE Transactions on Power delivery,2014,29(3):1 138-1 146.
[15]GHARTEMANI M K,KHAJEHODDIN S A,JAIN P K,et al.Addressing DC component in PLL and notch filter algorithms[J].IEEE Transactions on Power Electronics,2012,27(1):78-86.
[16]ELRAYYAH A,SOZER Y,ELBULUK M.Robust phase lockedloop algorithm for single phase utility interactive inverters[J].IET Power Electronics,2014,7(5):1 064-1 072.
[17]GOLESTAN S,MONFARED M,F(xiàn)REIJEDO F D,et al.Dynamics assessment of advanced single-phase PLL structures[J].IEEE Transactions on Industrial Electronics,2013,60(6):2 167-2 177.
[18]GOLESTAN S,MONFARED M,F(xiàn)REIJEDO F D,et al.Performance improvement of a pre-filtered synchronous reference frame PLL by using a PID-Type loop filter[J].IEEE Transactions on Industrial Electronics,2014,61(7):3 469-3 479.
[19]TUAN N,QUAN N,SANTOSO S.Improving performance of single-phase SOGI-FLL under dc-offset voltage condition[C]∥Proc.40th AnnualConf.IEEE IndustrialElectronics Society(IECON),2014:1 537-1 541.
Single-phase Fast Frequency Adaptive Frequency-locked Scheme under Distorted Grid Conditions
BEI Taizhou1,ZHANG Bowen2
(1.State Grid Jinan Power Supply Company,Jinan 250012,China;2.School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China)
Synchronous control and active islanding detection for the distributed grid-tied inverters need an accurate detection for the fundamental frequency of the grid.In order to obtain a high detection precision under the distorted grid conditions,based on the single-phase distributed grid-tied system,a frequency adaptive frequency-locked scheme is proposed with fast dynamic response performance.In the proposed scheme,the DC component and the harmonics are eliminated and rejected effectively by using the improved quadrature signal generator (QSG)and the cascaded complex filtering network presented in this paper,respectively.To ensure that the proposed scheme still has good performance under the frequency-varying situation,a frequency adaptive controller is built in the αβ-axes,for purpose of fast tracking the fundamental frequency of the grid.The feasibility of the scheme has been verified by simulation and experiment results.
grid synchronization;grid-tied inverters;harmonics rejection;complex filters;frequency adaptive control
TM76;TM46
A
1007-9904(2017)12-0016-07
2017-06-15
貝太周(1984),男,工程師,從事配電網(wǎng)運(yùn)維與狀態(tài)檢修、主動配電網(wǎng)優(yōu)化規(guī)劃及分布式光伏并網(wǎng)系統(tǒng)運(yùn)行與控制等工作。

