電力系統全過程動態仿真技術綜述

汪 湲 ，牟 宏 ，劉曉明 ，安 鵬 ，楊 斌

（1.國網山東省電力公司，山東 濟南 250001；2.國網山東省電力公司經濟技術研究院，山東 濟南 250021）

電力系統全過程動態仿真技術綜述

汪 湲1，牟 宏1，劉曉明2，安 鵬1，楊 斌2

（1.國網山東省電力公司，山東 濟南 250001；2.國網山東省電力公司經濟技術研究院，山東 濟南 250021）

電力系統全過程動態仿真是將機電暫態和中長期動態過程有機地統一起來進行的仿真計算。通過對電力系統長過程動態穩定特性的模擬分析，了解系統中長期失穩的動態特性機理，對電力系統規劃設計以及避免可能發生的大停電事故等有重要意義。對電力系統全過程仿真中遇到的主要問題，包括剛性系統求解特點、典型數值積分算法的優缺點、非線性代數方程迭代解法等做了闡述。最后，對目前國內外主流全過程動態穩定仿真軟件所應用的數值算法做了總結。

全過程動態仿真；剛性系統；變步長算法；中長期元件模型

0 引言

隨著特高壓骨干電網和智能電網的快速建設、直流輸電技術的迅猛發展、分布式發電和新能源技術的廣泛應用，我國電網將形成規模巨大的特高壓交直流復雜混聯系統［1-3］。系統結構、運行方式和動態行為更加復雜化。系統在暫態穩定后的中長期穩定問題逐漸成為威脅電力系統安全穩定運行的主要原因。國內外發生過多起大停電事故，其特點之一為持續時間長，大量中長期元件和控制措施發生作用［4-10］。

電力系統是典型的剛性非線性系統，仿真模型的時間常數差異很大，是快動態過程和慢動態過程的結合體。若要俘獲快動態過程，達到足夠的仿真精度，仿真步長要足夠??；要追逐慢動態過程，仿真時間又要足夠長。這本身是一個矛盾體。

傳統的暫態穩定不僅無法模擬鍋爐、AGC控制等中長期模型和控制措施，且要利用小步長仿真長過程動態計算代價相當大。因此，分析中長期動態過程的仿真技術就顯得尤其重要［11-12］。

在電力系統中長期動態過程仿真研究方面，國內外學者做了大量研究。美國電力科學研究院在20世紀70年代第一個完成中長期長期動態仿真程序，具備系統受到干擾后20 min的動態仿真能力［13］。法國電力公司參與完善和開發了電力系統機電暫態與中長期過程統一仿真程序STAG，更名為EURPSTAG［14］。日本東京電力公司和美國通用電力公司聯合開發了能夠仿真機電暫態和中長期動態的程序EXSTAB［15］。國內具有代表性的中長期動態仿真程序為中國電力科學研究院開發［16-18］。

而數值積分方法是整個全過程動態仿真的核心。根據電力系統不同時段的運行特點，選擇合適的數值積分方法以及相應的階和步長，既能保證數值穩定性，又能有效的控制誤差和提高仿真速度，成為整個數值積分算法的關鍵所在［1，19］。

本文簡述了中長期元件對電力系統穩定的影響，分析了剛性系統求解的特點，指出了電力系統分析中典型數值積分算法的優缺點，簡述了非線性代數方程的解法。最后，對目前國內外常用全過程動態穩定模擬軟件中的數值積分算法做了總結。

1 中長期元件對電力系統穩定的影響

在電力系統全過程動態中，必然伴隨著時間常數較大的元件和眾多自動控制保護裝置的動作。在暫態穩定分析中不予考慮的鍋爐、水輪機、自動發電控制、核反應堆、有載調壓變壓器、發電機過勵低勵限制器、解列控制、溫控負荷等模型，在全過程動態仿真中均需合理考慮［19］。這導致模型種類更加豐富，微分方程階數顯著升高。

電力系統的大崩潰常由連鎖反應事故引起，且時間跨度大，中長期元件的動態過程常常是導致電力系統失穩的主要原因。建立相應的中長期元件模型，通過全過程模擬，就可能更清晰地了解系統長過程失穩本質。這對提高我國電力系統分析水平、優化系統規劃設計以及研究防止系統大崩潰的有效調節措施等具有重要意義。

2 剛性系統特點及求解要求

2.1 剛性系統特點

剛性系統的時間常數差異很大，物理表現為系統中含有快動態分量和慢動態分量。若要俘獲快動態分量的變化過程，仿真步長要足夠??；而要獲得慢動態分量的變化過程，仿真時間又要足夠長。用很小的步長來仿真長過程，所耗費計算時間將無法接受。電力系統是典型的剛性系統，需采取適應剛性系統特點的算法來求解。

2.2 數值穩定性要求

在電力系統實際數值計算中，總會伴隨有各種各樣的誤差。一方面初始值y0不一定精確，另一方面計算機由于字長有限而在計算過程中會產生舍入誤差。這些誤差在數值計算過程中會不斷傳遞下去，而其大小是否會得到控制，就是數值穩定性問題。如果在數值計算過程中誤差的積累越來越大，那么所使用的算法是不穩定的；如果計算結果對初始數據誤差及計算過程中的誤差不敏感，那么所使用的算法是穩定的［21］。

在全過程動態仿真中，為了克服因數值穩定要求而帶來的步長限制，常要求數值方法的絕對穩定域包含整個左半平面，也即數值方法是A穩定的［20］。

A穩定是一種苛刻的限制，顯式多步法不可能是A穩定的。失去了顯式方法，差分后的非線性代數方程就需要用迭代法來求解，這加大了代數方程的計算過程，也即加大了每個仿真時步的計算量。用隱式方法在穩定性上解除了對仿真步長的限制，在一定的仿真時間內，相對于顯式方法總的計算步數大大減小。

考慮到電力系統的實際情況，在全過程動態仿真中采用的主要數值方法為1、2階吉爾法或隱式梯形法。隱式梯形法和1、2階吉爾法都是A穩定的。

2.3 速度及精度要求

對于電力系統全過程動態分析中所采用的隱式積分方法，理論上可以選取任意步長來提高仿真速度且能保證算法穩定性，但這顯然降低了仿真精度。精度也是仿真中必須保證的，仿真過程中誤差太大，結果也沒有利用價值。故需要在保證精度滿足要求的前提下，盡量提高仿真速度。

仿真精度以截斷誤差來描述，截斷誤差分為整體截斷誤差和局部截斷誤差。整體截斷誤差是整個仿真過程中的截斷誤差；局部截斷誤差是在假設以前各步計算沒有誤差的情況下當前仿真步長的截斷誤差。

對于全過程動態仿真中常用的隱式梯形法和1、2階吉爾法，列舉其局部截斷誤差。

1階吉爾法：

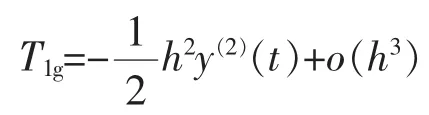
2階吉爾法：

隱式梯形法：

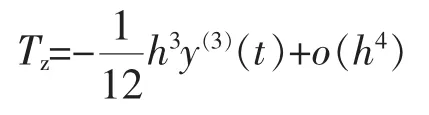
在電力系統全過程動態仿真中，在保證所求的解滿足給定精度的前提下，力求使計算量最小。這可以通過變階變步長來實現，也可以通過選擇不同的數值方法實現。設求解的時間區間為［a，b］，ε為整個區間的最大容許誤差，e為單位時間的最大容許誤差，則

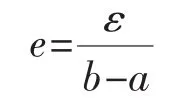
從而每個時步的最大容許誤差為。由以上各截斷誤差公式可見，誤差控制成為控制步長的主要因素，也是變步長算法的理論依據所在。

吉爾法是求解剛性系統的有效方法之一。在數值計算過程中，能夠根據系統的實際運行情況，自動選擇合適的階和步長，以期達到精度和速度的統一。吉爾法的主要計算步驟包括預測、校正迭代、截斷誤差計算和自動變階變步長控制4步［22］。

由于數值穩定性的需要，只選擇1、2階吉爾法計算。利用邊界軌跡法可以得到，1、2階吉爾法的絕對穩定域除覆蓋整個左半復平面外，還覆蓋右半復平面大部分。這樣對于本來不穩定的系統，如果計算步長選擇不當，可能計算出穩定結果，也即所謂的“超穩定”問題。為避免這種現象發生，需要合理減小仿真步長，這又導致仿真速度的減慢。因此，在有些電力系統全過程分析軟件中，對微分代數方程組的微分變量和代數變量分別處理：對微分變量采用隱式Adams方法，對代數變量采用吉爾法［23］。

大量的實踐表明，吉爾法在誤差控制和變步長控制上存在沖突。如果誤差控制嚴格，在機電暫態階段，仿真步長容易過小，而在中長期動態中可以得到合理的大步長；如果誤差控制放寬，雖然機電暫態階段步長合理，但中長期動態過程中，可能因累計誤差的過大而導致校正迭代不收斂，這又需要強制減小步長［1］。實際仿真中精度是必須保證的，這往往限制了暫態階段的仿真速度。

電力系統中的元件控制系統存在大量的限幅、死區等非線性環節。在系統的快動態過程中，大量的非線性環節起作用。吉爾法在預測階段無法預知非線性環節的可能發生，導致在校正階段或截斷誤差控制中該變量誤差很大。這將引起步長減小和雅克比矩陣的反復修改和分解，計算效率低下［1］。

固定步長的隱式梯形法在暫態穩定程序中得到了廣泛應用。限幅、死區等非線性環節大多在變量變化劇烈的暫態階段起作用。程序中隱式梯形法使用簡單迭代法求解，很容易處理控制系統的間斷環節。和吉爾法相比，在相同外部條件下隱式梯形法的誤差系數小，在暫態仿真中相同的誤差控制下，步長可以相對較大。常規的暫態穩定仿真步長在系統最小時間常數數量級，用簡單迭代法求解，不會影響非線性代數方程組的收斂性［20］。但在全過程動態仿真中，步長需要增大。簡單迭代法限制了仿真步長，故典型的暫態穩定程序不能擴展到全過程動態仿真。變步長的梯形積分法在美國ETMSP程序中應用。常規梯形積分法在網絡結構發生突變時容易引起數值振蕩，這限制了仿真步長的增加。為了增加計算步長，提高仿真速度，在發電機方程中加入了人工阻尼。這使得該程序無法進行阻尼特性方面的研究［20］。

在中國電力科學研究院開發的全過程動態仿真程序中，將固定步長的隱式梯形法和變步長的吉爾法有機地結合起來，根據系統的運行特點自動選擇數值算法，在保證數值穩定性和仿真精度前提下，顯著提高了仿真效率［1，24］。

2.4 非線性代數方程組的收斂性要求

選用合適的數值算法將微分方程差分化后，得到的是隱式非線性方程組。無論其與網絡方程交替求解還是聯立求解，都需要用迭代法。迭代求解的計算量和迭代初值有很大關系。為了減小計算費用，常用的是預估—校正法，即用一個顯式方法（預估式）給隱式方法（校正式）提供初值。

迭代求解常用的是簡單迭代法和牛頓迭代法。若用簡單迭代法求解，為使迭代收斂，仿真步長將被限制到最小時間常數的數量級。這與顯式數值方法對步長的要求無異，失去了采用隱式數值方法的優勢。若用牛頓迭代法求解，這種約束性將要減小很多，只需為Jacobi矩陣的合理近似。嚴格的牛頓法要求每次迭代都重新計算近似Jacobi矩陣及相應的逆矩陣，需耗費大量的計算時間。為了提高計算效率，程序中通常保持An+k不變，當迭代若干次不收斂時才重新計算，這稱為擬牛頓法。剛性初值問題通常Jacobi矩陣變化緩慢，不僅無需每次迭代重新計算An+k，而且不在每個積分步更新也是可能的，這大大減小了計算量。為了避免交替迭代求解帶來的交接誤差，程序中通常采用聯立求解［20，22］。

3 主要全過程動態仿真程序算法

目前，國內外常用的全過程動態仿真程序有美國EPRI的EMTSP／LTSP程序、法國和比利時聯合開發的EUROSTAG程序、美國通用電氣公司和日本東京電力公司共同完成的EXSTAB程序、瑞典和瑞士ABB公司開發的SIMPOW程序、美國PTI公司開發的PSS／E程序和中國電力科學研究院開發的電力系統全過程動態仿真程序等。

3.1 EMTSP／LTSP

LTSP為美國在其擴展的暫態穩定程序 （ETMSP）基礎上開發的長過程仿真程序。ETMSP采用變步長的隱式梯形法。為了削弱數值振蕩，增加仿真步長，程序在發電機中加入了人工阻尼。LTSP采用四階顯式龍格—庫塔法和隱式梯形法。根據預測的局部截斷誤差來改變仿真步長。通過在轉矩公式中加入人工阻尼來使長過程中所有發電機運行在同一頻率上［15，25］。

3.2 EUROSTAG

EUROSTAG程序在STAG程序上發展起來的，應用混合Adams-BDF算法。STAG采用經典吉爾算法，其絕對穩定域包含右半復平面大部分，故在計算時容易產生超穩定問題。Adams算法的絕對穩定域只包含左半復平面，用Adams方法對其微分代數方程組中的微分變量進行處理，就解決了所謂的“超穩定”問題。但Adams方法對代數變量的變化敏感，由于控制代數變量誤差需要，步長不能顯著增加，故對代數變量仍采用經典的吉爾法處理?；旌螦dams-BDF算法與經典的吉爾法的不同在于校正和截斷誤差估計中，代數變量和狀態變量的分別用不同的L向量［14，23］。

3.3 EXSTAB

程序暫態模式采用二階Adams向后積分公式，長過程模式采用基于θ的隱式自動變步長算法或準穩態算法?？筛鶕O置的尺度自動進行暫態模式和長過程模式的切換。長過程的兩種算法可以自動切換，也可以單獨使用。θ法使用方式靈活，根據的不同取值，可選擇隱式梯形法、改進歐拉法以及這之間的任何折中。θ的取值不同直接影響仿真速度、精度以及仿真中的數值振蕩方面。根據仿真中的最大局部截斷誤差和用戶指定誤差，可以自動調整步長［15，26］。

3.4 SIMPOW

程序采用吉爾法和隱式梯形法相結合的求解方式。根據變量性質的不同采用不同的積分方法。對剛性變量用BDF法，對非剛性變量用隱式梯形法。剛性度由估計的變化率和固定剛性度閾值比較決定。程序只有在系統發生大擾動時才更改Jacobi矩陣，以此來提高仿真速度［15，23，26］。

3.5 PSS／E

PSS／E采用隱式梯形法來仿真系統全過程動態，用戶根據經驗來改變仿真步長。實際仿真步長與用戶設定的仿真步長閾值來比較，決定程序運行在何種模式。不同的運行模式對系統做了相應的假設和處理。PSS／E開發者們認為步長應該由用戶控制而不應該由程序自動控制。用戶控制仿真步長，能夠知道所選仿真步長的假設條件和更好的理解仿真結果［26-29］。

3.6 電力系統全過程動態仿真程序

中國電力科學研究院通過比較吉爾法和隱式梯形法的優缺點，提出了一種組合數值算法。在其全過程仿真的機電暫態階段采用固定步長的隱式梯形法，動態元件的微分方程和電力網絡的代數方程進行簡單迭代求解；在中長期動態過程中采用變步長吉爾法，微分方程和代數方程聯立求解。兩種方法根據一定的策略自動切換，達到精度和速度 的 統 一［1，24，30］。

4 結語

全過程動態仿真因能更好地模擬系統長時域范圍變化特性而得到了越來越廣泛的應用。本文闡述了中長期元件對電力系統穩定性的影響，詳細介紹了剛性系統特點以及在求解過程中對數值穩定性、速度及精度、收斂性的要求。最后，對當前國內外主流全過程動態仿真程序所用數值算法做了總結。對特高壓交直流互聯背景下預防電力系統仿真計算具有一定指導作用。

［1］舒印彪.我國特高壓輸電的發展與實施［J］.中國電力，2005，38（11）：1-8.

［2］張運洲，呂健.我國未來同步電網的戰略構想［J］.中國電力，2006，39（3）：5-7.

［3］梁旭明，張平，常勇.高壓直流輸電技術現狀及發展前景［J］.電網技術，2012，36（4）：1-9.

［4］朱方，湯涌，張東霞，等.我國交流互聯電網動態穩定性的研究及解決策略［J］.電網技術，2004，28（15）：1-5.

［5］徐永禧.美國、加拿大 8.14 大停電［J］.國際電力，2003，7（5）：15-19.

［6］余曉丹，賈宏杰，陳建華.電力系統連鎖故障預測初探［J］.電網技術，2006，30（13）：20-25.

［7］印永華，郭劍波，趙建軍，等.美加“8.14”大停電事故初步分析以及應吸取的教訓［J］.電網技術，2003，27（10）：8-11，16.

［8］PATRICK D W，HANNAH D W.英國大停電事故中公眾信任度的定性研究［J］.電網技術，2007，31（20）：35-45.

［9］陳亦平，洪軍.巴西“11.10”大停電原因分析及對我國南方電網的啟示［J］.電網技術，2010，34（5）：77-82.

［10］陳竟成，黃瀚.印度大停電事故分析與啟示［J］.中國電力，2012，45（10）：12-16.

［11］常勇，王瑩，李立新.電力系統暫態穩定方法綜述［J］.云南電力技術，2009，37（6）：8-10.

［12］吳為，湯涌，孫華東，等.基于廣域量測信息的電力系統暫態穩定研究綜述［J］.電網技術，2012，36（9）：81-87.

［13］宋新立，湯涌，卜廣全，等.大電網安全分析的全過程動態仿真技術［J］.電網技術，2008，32（22）：23-28.

［14］STUBBE M，BIHAIN A，DEUSE J，et al.Stag-a new unified software program for the study of the dynamic behavior of electrical power systems［J］.IEEE Transactions on Power Systems，1989，4（1）：129-138.

［15］SANCHEZ-GASCA JJ，AQUILA RD，PRICE WW，et al.Variable time step，implicit integration for extended-term power system dynamic simulation［C］∥Power Industry Computer Application Conference，Salt Lake City，UT，1995.

［16］湯涌.電力系統全過程動態（機電暫態與中長期動態過程）仿真技術與軟件研究［D］.北京：中國電力科學研究院，2002.

［17］劉濤，戴漢揚，宋新立，等.適用于電力系統全過程動態仿真的風電機組典型模型［J］.電網技術，2015，39（3）：609-614.

［18］葉小暉，劉濤，宋新立，等.適用于全過程動態仿真的光伏電站有功控制模型［J］.電網技術，2015，39（3）：587-593.

［19］湯涌，宋新立，劉文焯，等.電力系統全過程動態仿真中的長過程動態模型—電力系統全過程動態仿真軟件開發之三［J］.電網技術，2002，26（11）：20-25，52.

［20］徐緒海，朱方生.剛性微分方程的數值方法［M］.武漢：武漢大學出版社，1997.

［21］藺小林，蔣耀林.現代數值分析［M］.北京：國防工業出版社，2004.

［22］劉德貴，費景高.動力學系統數字仿真算法［M］.北京：科學出版社，2000.

［23］ASTIC J Y，BIHAIN A，JEROSOLIMSKI M.The mixed Adams-BDF variable algorithm to simulate transient and long term phenomena in power systems［J］.IEEE Transactions on Power Systems，1994，9（2）：929-935.

［24］湯涌.交直流電力系統多時間尺度全過程仿真和建模研究新進展［J］.電網技術，2009，33（16）：1-8.

［25］EPRI，USA.Extended transient-midterm stability package，final report［R］.EPRI，Palo Alto，California，USA，1987.

［26］Simens Power Transmission＆Distribution，Inc.PSS／E 31.0 online documentation［Z］.USA，2003.

［27］宋新立，湯涌，劉文焯，等.電力系統全過程動態仿真的組合數值積分算法研究［J］.中國電機工程學報，2009，29（28）：23-29.

［28］FANKHAUSER H R，ANEROS K，EDRIS A，et al.Advanced Simulation Techniques for the Analysis of Power System Dynamics［J］.IEEE Computer application in power，1990，3（4）：31-36.

［29］DE MELLO F P，FELTES J W，LASKOWSKI T F，et al.Simulating Fast and Slow Dynamic Effects in Power Systems［J］.IEEE Computer Applications in Power，1992，5（3）：33-38.

［30］宋新立.電力系統全過程動態仿真絲算法與模型研究［D］.天津：天津大學，2014.

Overview of Power System Full Dynamic Simulation Technology

WANG Yuan1，MU Hong1，LIU Xiaoming2，AN Peng1，YANG Bin2
（1.State Grid Shandong Electric Power Company，Jinan 250001，China；2.Economic&Technology Research Institute，State Grid Shandong Electric Power Company，Jinan 250021，China）

The full dynamic simulation combines electromechanical transient process and mid-long term dynamic process.Through simulation of the power system dynamic characteristics，to understand the mid-long instability mechanisms，it has great significance to power system plan and to avoid blackout.The main problems in the power system full dynamic simulation are introduced in the paper，including mid-long term solution characteristics of rigid system，advantages and disadvantages of typical numerical integration algorithms，iterative method for solving nonlinear algebraic equations.Finally，the character of the algorithms used in the mainstream simulation tools for full dynamic simulation are summarized.

full dynamic simulation；rigid system；variable step size algorithm；mid-long term component model

TM715

A

1007－9904（2017）12－0023－05

2017-06-26

汪 湲（1978），女，高級工程師，從事電網規劃工作。