從單擺到微分方程近似解的新解法

從高中物理教材對單擺簡諧性質的介紹出發，更深一步認識簡單的擺的運動性質和視為簡諧運動的條件，聯系單擺作為計時器件的不足。通過用不同方式化簡微分方程和使用計算機計算數值解并繪圖，針對單擺模型的理論計算和現實中的摩擦阻尼試進行進一步討論。

在高中物理選修課上我們已學習過單擺系統在小角度擺動的條件下可以近似為簡諧運動，并了解了通過單擺測量當地重力加速度的值；在實驗中，我們得到了與實際值較為符合的實驗結果，可見這樣的近似是合理的。然而，在實際生活中擺角并不能做到很小，否則單擺的能量很快回衰減到0，同時也會給測量上帶來困難。因此在實際生活中，單擺的周期存在一定的誤差，進一步計算表明，當擺角為5°時周期誤差小于0.5%。本文討論單擺在非小角度情況下的運動規律，得到非小角度下單擺周期的修正公式，并以此為基礎討論其在實際生活中的應用。誠然，單擺作為力學經典模型之一，其理論和各個方向的應用早已被討論透徹，但從學生的角度還有一些東西可以發掘探究。

求理想模型中單擺的周期

初解方程

假設單擺長l，小球質量為m，初始擺角為α，空氣摩擦不計。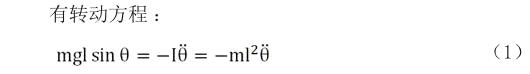

從表中我們可以看到，當單擺的擺角增大時，單擺周期也隨之增大，并且偏差有加速增加的趨勢。

修正周期公式

1）通過待定系數求解。

單擺在任意位置的運動狀態都是確定的，因此即使在大角度下單擺依舊做周期運動，只是周期和周期內角度關于時間的分布有所改變。因此，我們不妨假設新的單擺仍做簡諧運動，并通過待定系數法求解使得在某一最大擺角下最貼近真實運動的ω。

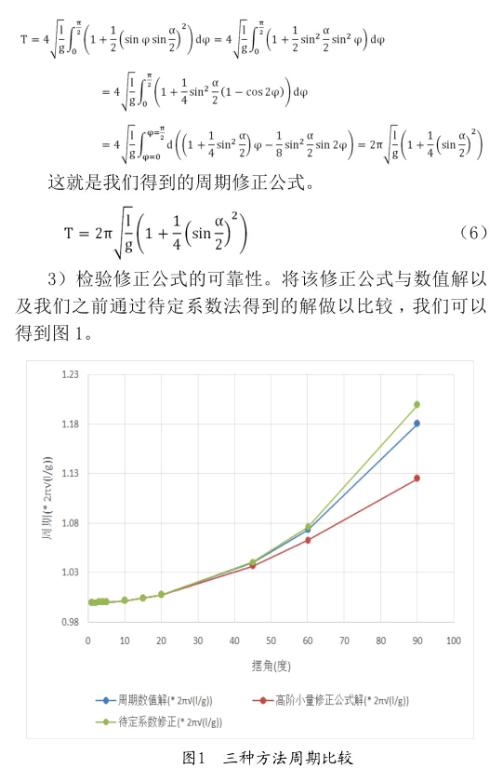
可以看到，待定系數方法修正的結果與實際情況最為接近，即使在60度的擺角之下，依然和數值解符合的很好。而高階小量修正法的結果更加簡潔明了，易于應用。另外，在“通過高階小量展開近似求解”的討論中，我們將其（1）的式子展開到二次項，但只將其（2）的式子展開一次項，結果卻發現后者更精確，這也是很有意思的。

在實際中的應用

擺鐘很早就被廣泛應用于實際生活中。如果不能夠充分考慮較大擺角下面周期變化，可能使得擺鐘有較大的誤差。

考慮空氣阻力

定性分析：在一個單擺周期中，空氣阻力產生的作用大約一半朝正放向，一半朝負方向，但總阻礙小球擺動。鑒于空氣阻力始終與單擺運動方向相反，因此可以預見，由于空氣阻力的存在，單擺的周期會有所變長。同時，當小球質量不太小，最大速度不太大時，系統在一個適合觀察的時段內擺動幅度縮小不太過明顯，可近似認為做周期運動。

對此方程，在各項數值確定的情況下可以方便地通過計算機做出將來的運動圖像，由此即可與理想狀況進行比較。

其他在單擺中存在而能夠被忽略或較難以研究的因素

考慮地球引力場是有心力場；考慮地球參考系中由地球自轉產生的科里奧利加速度；懸繩所掛節點在多次扭轉過程中產生的熱量損失；繩能被視作具有非常大勁度系數的彈性繩等。

結論

雖然單擺在實際生活中的作用已經逐漸減小，但是在單擺求解過程中的思考卻可以給我帶來很多啟發。本文從單擺的大角度求解出發，從數值求解，泰勒展開求解以及待定系數優化誤差三個角度分別討論了單擺在大角度情況下周期的變化，并驗證了，我們所提出的泰勒展開法與待定參數法所得到的結果與實際結果在60度的大擺角的情況下依然相當吻合。

同時基于誤差最小優化參數的方法是我們獨立提出的具有創新性的一種微分方程的新解法，這對微分方程近似解求解有著積極的指導作用。

參考文獻

[1]劉鳳祥.單擺運動周期的近似解[J].大學物理，1999，18（11）：5-7.

[2]黃秀蘭.單擺周期近似解的討論[J].云南師范大學學報（自然科學版），1995（2）：38-45.

[3]譚志忠.求大擺角單擺周期近似解的“局部常化”方法[J].大學物理，2005，24（12）：14-17.

（作者簡介：朱嘉瑋，江蘇省丹陽高級中學。）endprint